新中考下创新能力题教学案例探析

王忠海

自初中新课程标准实施以来，能力的培养一直是课程标准中的主线，分析近年来浙江省各市实施新课标的中考卷，都呈现出考查基础、注重过程、渗透思想、突出能力、强调应用、鼓励探究和创新的特点．中考数学试卷从试题结构到内容设计，题型活泼，情景新颖，不在计算技巧和知识立意的试题上过分纠缠，而是注重各种题型的结合和题量的适度，深化能力立意，出现了很多探究性、操作实践性、阅读理解和开放性等考查创新能力的好试题．

现把近年来中考中出现的新题型从教学的角度做一个归纳，希望能对中考复习的师生有所帮助．

一、探究性试题

开展探究性学习，不仅是为了适应当前中学课程改革中产生的研究性课程教学，

更重要的是为培养学生的创新精神和实践能力，真正实现素质教育的需要．

【例1】 如图1，这些等腰三角形与正三角形的形状有差异，我们把这与正三角形的接近程度称为“正度”．在研究“正度”时，应保证相似三角形的“正度”相等．

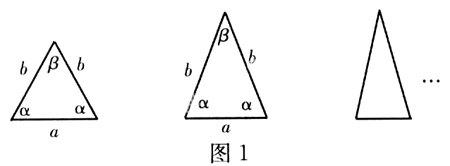
设等腰三角形的底和腰分别为a，b，底角和顶角分别为α，β．要求“正度”的值是非负数．

同学甲认为：可用式子|a-b|来表示“正度”，|a-b|的值越小，表示等腰三角形越接近正三角形；

同学乙认为：可用式子|α-β|来表示“正度”，|α-β|的值越小，表示等腰三角形越接近正三角形．

探究：（1）他们的方案哪个较合理，为什么？

（2）对你认为不够合理的方案，请加以改进（给出式子即可）；

（3）请再给出一种衡量“正度”的表达式．

点评：数学探究性教学模式要树立新的教学观和学生观——教学过程的意义不仅在于使学生获得知识，更重要的是使每一个学生都能获得身心的充分发展，体味到学习乐趣，从而激发学生主动学习和兴趣．

二、开放性试题（问题变式教学）

开放题是中考题多样化和时代发展要求的产物，单一的题型和测试目标限制了考生应用知识解决实际问题的能力，不利于激发学生的创造性．开放性试题能为考生提供更大的考虑问题的空间，在解题途径方面也是多样的，这样的试题是十分有利于考生发挥水平，也有利于考生创新意识的培养．

1.条件开放与探索

条件开放探索题的明确特征是缺少确定的条件，问题所需补充的条件不是得出结论的必要条件，所需补充的条件不能由结论推出．

【例2】 已知：∠MAN＝30°，O为边AN上一点，以O为圆心，2为半径作⊙O，交AN于D，E两点，设AD＝x．

（1）如图2-1，当x取何值时，⊙O与AM相切；

（2）如图2-2，当x为何值时，⊙O与AM相交于B，C两点，且∠BOC＝90°．

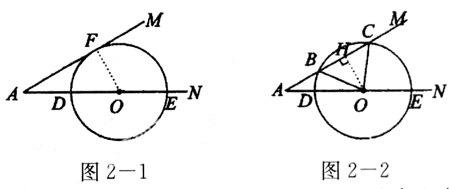
点评：解答这类问题往往是把结论反过来当条件用，本例可利用圆的切线性质和垂径定理，构造特殊直角三角形，使问题得以求解．

2.结论开放

【例3】 已知矩形ABCD和点P，当点P在边BC上任一位置（如图3-1所示）时，易证得结论：PA²＋PC²＝PB²＋PD²，请你探究：当P点分别在图3-2、图3-3中的位置时，PA²、PB²、PC²和PD²又有怎样的数量关系？请你写出对上述两种情况的探究结论，并利用图3-2证明你的结论．

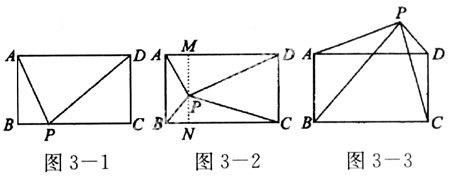
点评：本题也是一道结论开放题，通过阅读题目已知条件及要求，不难探究出正确结论，但是说明理由时，有一定的难度．正确作出辅助线，创造性地使用勾股定理的条件，是解决问题的关键．

3.综合开放

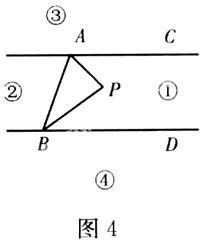
【例4】 如图4，直线AC∥BD，连结AB，直线AC，BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连结PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角．）

（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；

（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立（直接回答成立或不成立）？

（3）当动点P在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．

点评：开放题的特征很多，如条件的不确定性，它是开放题的前提；结构的多样性，它是开放题的目标；思维的多向性，它是开放题的实质；解答的层次性，它是开放题的表象；过程的探究性，它是开放题的途径；知识的综合性，它是开放题的深化；情景的模拟性，它是开放题的实践；内涵的发展性，它是开放题的认识．过程开放或结论开放的问题能鼓励学生多角度、多侧面、多层次地思考问题，有助于充分调动学生的潜在能力．

三、操作性问题

《数学课程标准》在描述空间观念的主要表现时，提到了“能从复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系”，学生是否能达到这样一个要求，与其头脑中的图形表象有着密切的关系．事实上，学生形成图形概念的过程就是一个图形的表象不断积累，并对这些积累的表象不断加工提炼的过程．如何不断积累图形的表象，特别是涉及其大量变式的表象，经历与图形有关的各种操作活动是一个非常重要的途径．在认识图形的过程中，学生不断做出所要认识的各种图形，教师也不断将各种图形提供给学生操作，学生更是通过相互间的交流看到了更多的图形，这种对首次感知的强化和大量的图形表象的积累为学生进一步提升对图形的理性认识奠定了基础．

【例5】 （2007，绍兴）学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的（如图5-1～5-4）：

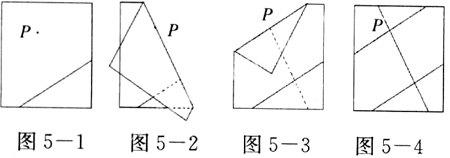
从图中可知，小敏画平行线的依据有（）．

①两直线平行，同位角相等；②两直线平行，内错角相等；

③同位角相等，两直线平行；④内错角相等，两直线平行．

A．①② B．②③ C．③④ D．①④

【例6】 （2007，浙江）如图6-1，小明将一张矩形纸片沿对角线剪开，得到两张三角形纸片（如图6-2），量得他们的斜边长为10@cm，较小锐角为30°，再将这两张三角纸片摆成如图6-3的形状，但点B、C、F、D在同一条直线上，且点C与点F重合（在图6-3至图6-6中统一用F表示）.

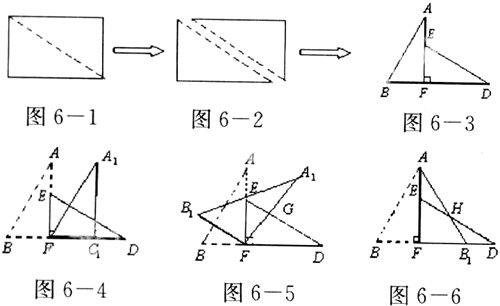
小明在对这两张三角形纸片进行如下操作时遇到了[HJ0.85mm]三个问题，请你帮助解决．

（1）将图6-3中的△ABF沿BD向右平移到图6-4的位置，使点B与点F重合，请你求出平移的距离；

（2）将图6-3中的△ABF绕点F顺时针方向旋转30°到图6-5的位置，A1F交DE于点G，请你求出线段FG的长度；

（3）将图6-3中的△ABF沿直线AF翻折到图6-6的位置，AB1交DE于点H，请证明：AH=DH.

四、阅读理解、规律探索题（合情推理问题）

【例7】 （2007，温州）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的长度构造如下正方形：

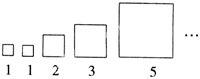
再分别依次从左到右取2个、3个、4个、5个，正方形拼成如下矩形并记为①、②、③、④，相应矩形的周长如下表所示：

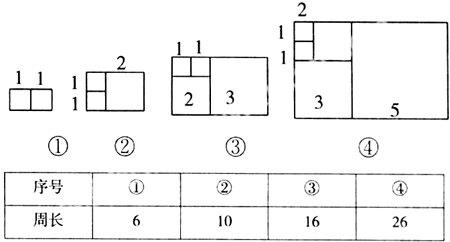
若按此规律继续作矩形，则序号为⑩的矩形周长是________．

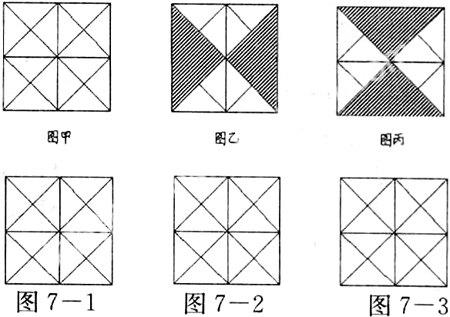
【例8】 （2007，绍兴）如图甲，正方形被划分成16个全等的三角形，将其中若干个三角形涂黑，且满足下列条件：

（1）涂黑部分的面积是原正方形面积的一半；

（2）涂黑部分成轴对称图形．

如图乙是一种涂法，请在图7-1～7-3中分别设计另外三种涂法．（在所设计的图案中，若涂黑部分全等，则认为是同一种涂法，如图乙与图丙）

“创新是一个民族的灵魂，是国家兴旺发达的不竭源泉”．而实际上不少学生的知识结构单一，应用意识淡薄，创新能力较弱．为此我们有必要补充创新试题，这也正是解决这一弊端的有力手段．

［责任编辑：金 铃］