巧用“线变题”破解相贯线投影规律之教学难点
2009-08-17沈妙君
摘要:《机械制图》课程的主要目的之一是培养学生空间想象能力和形象思维能力。该课程离不开投影制图,而相贯线投影又是重点和难点。如何破解相贯线的投影规律是需要教师帮助学生解决的重要问题。
关键词:线变题;相贯线投影;基本体;造型
在《机械制图》课程中,相贯线投影是投影制图的重要组成部分,是使学生树立空间概念,培养空间想象能力的一个重要的突破口。这部分内容的掌握与否,直接影响到学生读图能力的强弱。对于高一学生来说,相贯线投影是制图课程学习初期的一只“拦路虎”。究其原因,主要有三点:第一,相贯线是由两个几何体相互贯穿或相交后自然形成的表面交线,而基本几何体种类繁多,诸如棱柱、圆柱、圆锥、球等,从而使得两两组合的相贯线形状千变万化;第二,相贯线大多为圆柱穿孔,因其不可见性,导致不容易直接从模型上观察到;第三,相贯线的教学内容一般被安排在教材的第五章,而在此之前,学生只是刚刚接触过点、线、面的投影基础,对空间形体的信息储存量尚不足。因此,如何破解相贯线的投影规律是需要教师帮助学生解决的重要问题。
“线变题”的理论基础
所谓“线变题”是指通过视图中某一线条的变化反映基本体形状、尺寸与位置变换的习题。教学实践中,教师可从小范围的变换着手,区分异同,再从一系列的类比中得出相贯线投影规律,由小见大,由浅入深,逐步培养学生的读图能力,使他们树立空间的概念。下面通过四例“线变题”讨论帮助学生掌握相贯线投影规律的问题。
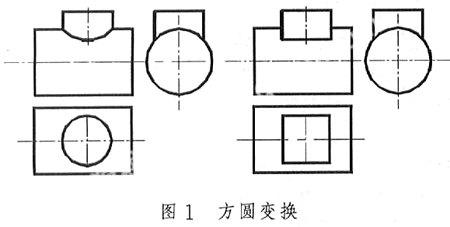
方圆变换在职业高级中学的制图课程中,相贯线大多是由圆柱、长方体这两个最主要的基本体相交而形成的,其中尤以两圆柱垂直相交或圆柱与长方体垂直相交最为普遍,但两者的相贯线形状却大相径庭。试比较图1的两张俯视图,其中仅有一处线条发生了变换,即由左边的圆形变成了右边的方形。根据基本体的投影规律,其实质是基本体圆柱与长方体的相互转换,随着基本体类型的变换,相贯线形状也随之发生了变化,由原来的两圆柱垂直相贯改为圆柱与长方体垂直相贯,主视图中的相贯线投影形状也由曲线相应地变为直线。
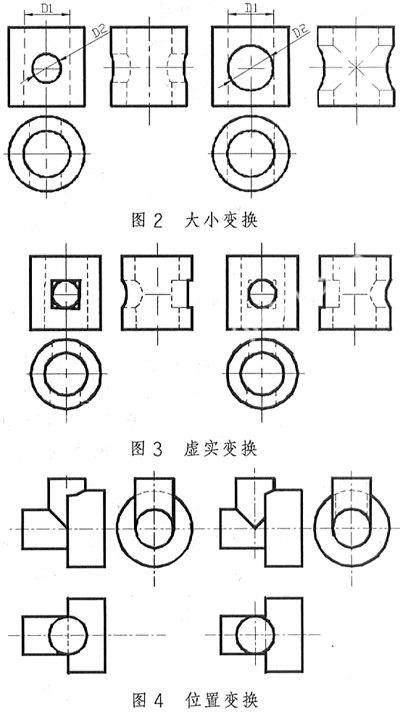
大小变换将图2主视图中圆的直径由小变大,从原来小于虚线孔径变为等于虚线孔径,随着该基本体圆柱大小的变换,相贯线形状也相应地发生了改变。显然,当两圆柱直径D1≠D2时,相贯线形状为弯向大圆柱轴线的曲线;当两圆柱直径D1=D2时,相贯线形状为过两圆柱轴线交点的直线。
虚实变换在投影作图中,若把视图中的虚线与实线对换,则其部分结构的位置会发生变化,如图3所示。虚实变换从表面上看是可见与不可见性的分析判别,其实质是基本体结构的方位分析,需要让学生深刻认识“高见低不见”、“前见后不见”、“左见右不见”的投影规律,从而进一步了解形体分析的实质。
位置变换随着俯视图中圆的左右位置的变换,当然其实质是基本体圆柱位置的变换,即随着这一圆柱位置的左右移动,它与其他两个大小圆柱之间的相交范围就会发生改变,即由左边俯视图的各一半变为右边的一大一小,那么它的主视图与侧视图也就相应地发生了改变,如图4所示。如果该圆柱的位置改为右移,情况又会略有不同。
通过对上述四例比较典型的“线变题”的分析,可以更加清晰地认识到相贯线的投影,其实质就是反映两基本体间的大小、形状与位置的变换。这样一来,相贯线的投影规律也就不难总结了:
其一,当两基本体为垂直相交的圆柱,且两圆柱直径不等时,则相贯线在两圆柱均不反映圆的视图上的投影为弯向大圆柱轴线的曲线;而当两个圆柱直径相等时,相贯线则为过两轴线交点的直线。
其二,当两基本体为垂直相交的长方体和圆柱,且圆柱的直径等于长方体宽度时,其实质为圆柱与长方体相切,相贯线在圆柱不反映圆的视图上的投影为长方体的轮廓线画到切点,且光滑过渡;而当圆柱的直径不等于长方体宽度时,其实质为圆柱与长方体相交,长方体的轮廓线则画到交点,且有交线。
根据上述投影规律,学生在千变万化的习题中,只要能分析出两基本体所处的状态(是否垂直相交,谁大谁小),就能相对顺利地读懂视图,求出其投影。
“线变题”的组织与应用
课前精编线变题 “线变题”的组织,关键在于教师的课前准备工作。教师要对习题进行筛选、编排,把一系列相似的有层次的题目归为一类,比较异同点,以便更加方便地导入相贯线的投影规律,引导学生由浅入深地提高空间想象能力与思维能力。对于刚刚接触相贯线投影的学生,教师可从三个层次编题:第一,两实心圆柱的相贯;第二,实心圆柱穿孔;第三,两空心圆柱相贯。这样,由实心到空心,由可见到不可见,由只有两个圆柱垂直相交到三个甚至四个圆柱垂直相交,一步步地加深难度,学生就比较容易接受了。当然,对于理解能力不同的学生,要求可以有所区别。
课中巧用三维造型相贯线大多为穿孔造型,其内部虽不可见,却又是实实在在存在的。俗话说“眼见为实”,在日常生活中我们所接触的实物大多只能看到其外表面,对于内部或者说孔与孔之间的关系则无法看清楚。所以,当学生对空间感到困惑时,让他们“眼见为实”就显得十分必要,三维立体造型就是非常不错的教学模型。它可以顺利地对各种相贯基本几何体进行形象分解与透视,并且可以轻易地从不同角度进行转换。基本上所有题目都可以利用三维立体造型,非常方便。运用三维立体造型进行形象的分析与讲解,更容易使学生的识图能力得到提高。
课后的归纳与总结“线变题“的组织实质是根据教材内容,按照大纲要求,把相贯线投影的知识点进行分块、分层讲解。考虑到该阶段学生的空间想象能力比较有限,在具体教学实践中,教师应把教学内容讲得透彻一些,并在教学完成后加以适时的归纳与总结。否则,尽管教师课前辛苦准备,课上讲得滔滔不绝,而学生课后仍是云里雾里不知其所以然。因此,利用下课前10分钟的时间帮助学生进行必要的知识归纳与梳理是十分必要的。
参考文献:
[1]王幼龙.机械制图[M].北京:高等教育出版社,2001.
[2]劳动和社会保障部.机械制图[M].北京:中国劳动社会保障出版社,2001.
[3]北航CAXA教育培训中心.CAXA实体设计XP—创新三维CAD教程[M].北京:航空航天大学出版社,2003.
作者简介:
沈妙君(1976—),女,浙江宁波人,浙江宁波鄞州职业高级中学一级教师,研究方向为机械专业教学。
