水工钢闸门轨道横截面弯曲应力分析

白润波，曹平周，邱丽清

（1.河海大学土木工程学院，南京 210098；2.山东农业大学水利土木工程学院，山东泰安 271018）

水工钢闸门轨道横截面弯曲应力分析

白润波1，2，曹平周1，邱丽清1

（1.河海大学土木工程学院，南京 210098；2.山东农业大学水利土木工程学院，山东泰安 271018）

水工钢闸门轨道纵向应力实测值与我国现行规范计算值差异较大。采用理论推导、数值计算、有限元求解的方法对这一问题进行研究。研究表明水工钢闸门轨道特殊的受力和边界条件，是轨道横截面正应力分布异于初等梁理论的原因。轨道与混凝土基础的水平摩阻力使轨道底面弯曲应力有较大幅度下降，轮轨接触局部荷载的作用与弯矩的叠加效应使轨道顶部横截面的正应力有大幅度提高。提出的计算公式可供计算轨道底面和顶面的最大弯曲应力。其分析很好地解释了三峡工程高压闸门定轮支承结构试验中轨道弯曲应力测试的现象。

钢闸门；轨道；弯曲应力；摩擦；局部应力

在三峡水利枢纽高压闸门定轮支承结构试验［1］中，轨道横截面上最大弯曲应力实测值与我国现行规范［2］计算值相差很大，该处上翼缘最大弯曲压应力实测值比规范计算值高出较多，下翼缘最大弯曲拉应力实测值比规范计算值小很多。此种现象在文献［3］中也有描述。目前，对于水工钢闸门轨道弯曲应力国内外研究较少，本文对水工钢闸门轨道弯曲应力进行研究，对试验现象给出理论解释。

1 水工轨道弯曲应力研究现状

工程中水工钢闸门轨道为竖向布置，但在模型试验时，受试验条件限制，分析模型一般取轨道水平放置，因此理论分析时通常也取轨道水平放置构建分析模型，如图1（a）、（b）。在进行水工钢闸门轨道弯曲应力计算时，我国现行规范将轨道看作支撑于轮轨接触处的倒置悬臂梁，如图1（c），并利用初等梁理论计算轨道横截面弯曲应力，公式为

式中：W为轨道截面抵抗矩；M为轨道最大弯矩；M＝3Ph／8；P为轮压；h为轨道截面高度。国外的标准、规范［4，5］多建议采用Winkler弹性地基上梁模型计算轨道弯曲应力。这两种模型的计算结果都与文献［1］、［3］的试验现象相差很大。实际上，对地基比较坚硬且接触面比较粗糙的情况，梁与地基的水平摩阻力效应会使梁的最大弯矩有较大幅度下降［6］，这可能是水工钢闸门轨道下翼缘弯曲应力值较低的主要原因；轨道上翼缘最大弯曲应力计算点处正是轮轨接触部位，此处轨道横截面的正应力应为按接触问题求出的纵向应力与由弯矩引起的弯曲应力的叠加，表现为上翼缘的弯曲应力变大。规范中计算轨道横截面弯曲应力实际上是对轨道中近似呈单轴应力状态的横截面正应力的验算，轨道横截面正应力可分解为由弯矩引起的弯曲应力和由轮轨接触局部荷载引起的纵向应力，在轨道底部主要是弯曲应力，在轨道顶部则需计算两者之和，并涉及单轴应力状态点的寻找问题。本文采用理论推导、数值计算、有限元求解的方法对这一问题进行研究。

图1 轨道受力图及计算模型Fig.1 Force diagram of track and computationalmodel

2 考虑基础混凝土对轨道的水平摩阻力时轨道的弯曲应力分析

采用考虑水平摩阻力的弹性地基梁模型进行分析。混凝土基础被视为具有水平和竖向反力的弹性支承体，基础的竖向反力采用Winkler地基假设，即竖向反力与该点的沉陷成正比，水平反力假设与轨道底同基础之间的相对水平位移成正比。基础的竖向反力qv和水平反力qu可表示为（图2）

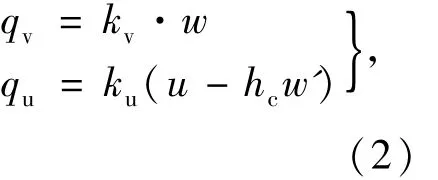
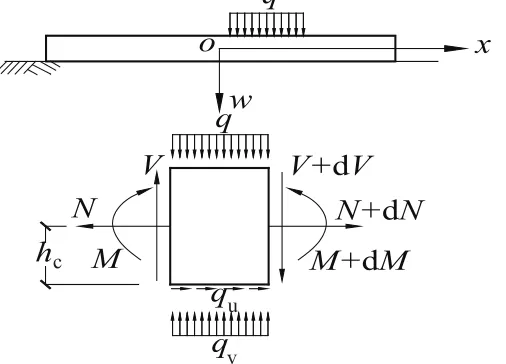
图2 考虑摩擦的弹性地基上轨道染模型Fig.2 Track model considering beam on elastic foundation with friction

轨道的挠曲线方程和轴向力与截面位移的关系为

式中E，I和A分别为轨道的弹性模量、惯性矩和截面积。在上述公式（2）、（3）、（4）方程中消去轨道的内力，得到如下的微分方程组

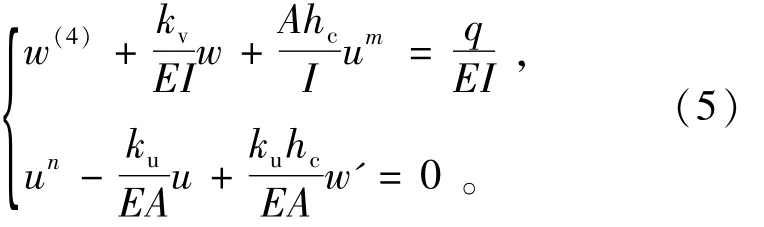
式（5）的特征方程为

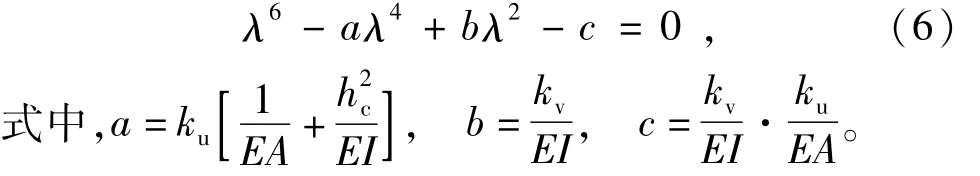
对无限长梁上作用一集中力P的情况，根据边界条件可得梁的最大弯矩Mm为

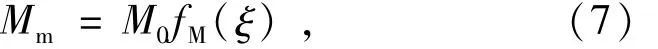
式中：kv，ku分别为基础竖向和水平向的刚度系数；w，u分别为轨道的竖向挠度和截面水平位移；hc为轨道中性轴到轨道底的距离。

取长度为d x的一段轨道分析建立平衡方程（图2），可得轨道的内力—弯矩M，剪力V，轴向力N的关系式为

式（7）的求解很繁复，没有显式解答，且系数kv，ku难以确定。对水工钢闸门轨道与基础混凝土这种情况，最大弯矩会较不考虑摩擦时减小多少从解析上不容易判定。为此采用有限元方法对这一弯矩折减系数进行研究。在轨道与基础混凝土之间设置接触对，摩擦系数μ＝0时的解答与Winkler地基梁解相对应。由于轨道埋入二期混凝土中，轨道除顶面外周围都有较大体积的混凝土对轨道起约束作用，可以假定轨道底面的混凝土与轨道的接触面位移连续，既没有相对滑移，也没有脱离，此时可认为μ＝∞。若取轨道与基础混凝土的摩擦系数为0.4［7］，计算得到的轨道底部弯曲应力与μ＝∞时相差很小，本文取μ＝∞进行分析。考虑轨道高度h和混凝土强度等级的影响，以弯曲应力的折减系数η＝σμ＝∞／σμ＝0来表示弯矩折减系数。η随轨道高度h和混凝土基础弹性模量Ec变化的关系图如图4（a）所示，由图可见，η受h变化的影响很小，与Ec近似呈线形关系。图4（b）为不同h下η的平均值与Ec的关系图，η与Ec的关系可用如下公式拟合，

η＝0.8-0.72β ，（8）式中，β是取相应Ec以105MPa为单位时的数值。式（8）与有限元结果的偏差最大为0.4%。

当kv取值不同时，由公式M0／W计算的弯曲应力也发生变化。图5为不考虑摩擦时按不同方法计算得的弯曲应力与规范计算值的比较，可见，规范计算值居中，其他计算方法与它的最大差值为±18%。规范计算公式相对简单，M0可按规范公式计算，即M0＝3Ph／8。

图3 函数fM图Fig.3 Diagram of function fM

图4 弯曲应力折减系数Fig.4 Reduction coefficient of bending stress

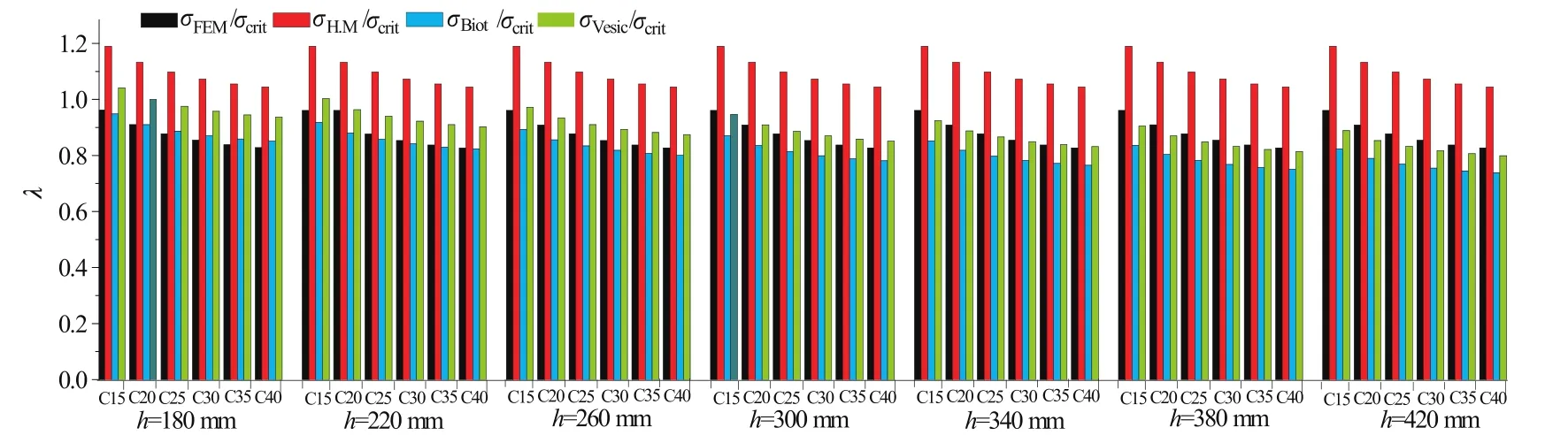
图5 不同方法计算得的弯曲应力比较（不考虑摩擦）Fig.5 Comparison of bending stresses by differentmethods（without regard to friction）

由此，可得考虑轨道与基础混凝土水平摩阻力时水工钢闸门轨道横断面最大弯矩为

相应的轨道底面最大弯曲应力可按下式计算，

3 轮轨接触局部荷载引起的纵向应力

对轮轨接触附近小区域内应力的分析可采用半平面体在水平直边界上受分布力的模型来分析，如图6。在d s长度上的分布力p（s）d s在平面体内任一点产生的应力为［9］

按赫兹理论，轮轨接触分布力沿x轴方向为椭圆形分布（图7），应力表达式为

式中：p0为滚轮与轨道间最大赫兹接触应力，p0＝ 0.418为轮缘宽度，R为滚轮半径，E为材料的弹性模量；a为轮轨赫兹接触半宽。

图6 半平面体在边界上受分布力Fig.6 A half plane body compressed by a distributed force in its boundary

图7 接触应力分布Fig.7 Distribution of contact stress

把式（12）代入式（11）并积分可求出此时轨道内部的应力为

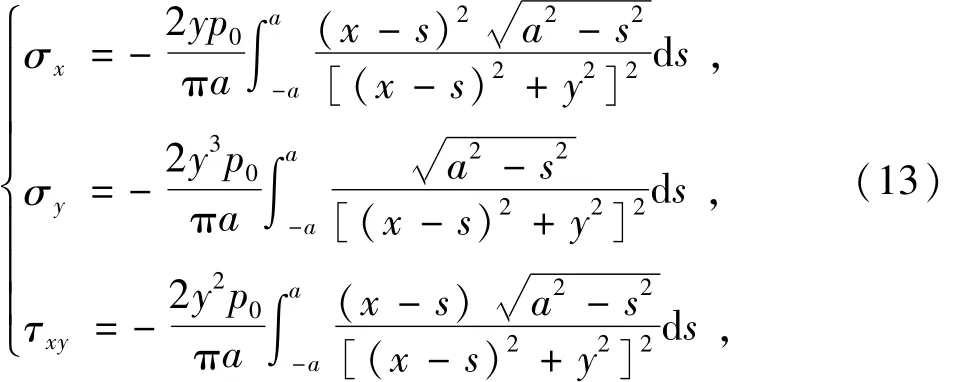
在接触分布应力作用区内，轨道顶面附近处于多向应力状态（三向受压，平面问题为双向受压），应按折算应力计算。图8为按式（13）计算的x∈［1.0a，3.6a］，y∈（0，1.4a］（坐标系同图7）范围内轨道应力分布图，可见，在离开接触应力作用区很近的区域内仍然是多向应力状态，但各向应力都迅速减小。在离轨道表面很近的位置处纵向应力较其他向应力大很多，呈现近似单轴应力状态，如图9所示，在靠近x＝1.0a且其他向应力占纵向应力比例小于10%的地方，纵向应力约为0.08p0。由于a一般很小，该位置处弯矩与M′0差别很小，可以M′0计算。此处由接触产生的纵向应力与由弯矩引起的弯曲应力叠加便是轨道顶面上横截面的计算正应力，

图8 x∈［1.0a，3.6a］，y∈（0，1.4a］范围内轨道应力分布Fig.8 Stress distribution of track in the range of x∈［1.0a，3.6a］，y∈（0，1.4a］

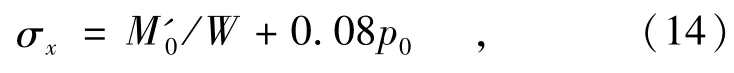
式中，M＇0按式（9）计算。

图9 轮轨接触区外轨道顶面应力分布Fig.9 Stress distribution of top track outside contact zone between track and wheel

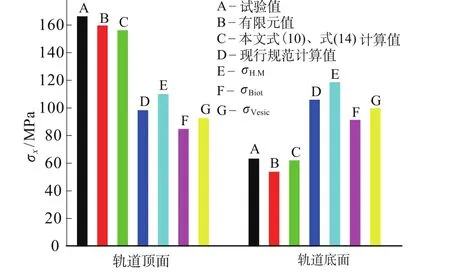
图10 本文模拟公式计算值与其他方法计算值比较Fig.10 Comparison between calculated values by formulas in this article and othermethods

4 模型验证

对轨道横截面弯曲应力计算时应分轨道底部和轨道顶部分别验算。轨道底部弯曲应力可按式（10）计算，轨道顶部弯曲应力可按式（14）计算，式（14）计算得的实际为轨道横截面正应力。为验证上述计算模型及拟合公式的可靠性，以三峡水利枢纽高压闸门定轮支承结构试验模型为计算对象，几种计算方法的结果对照见图10；σH.M，σBiot，σVesic的意义同图5；轨道顶面为弯曲压应力，轨道底面为弯曲拉应力，图中数值均取绝对值。可见，本文所提公式计算值与试验值和有限元分析值较为接近，能较好地反映水工钢闸门轨道横截面的正应力状态。现行规范计算方法有可能导致不安全的结果。

5 结 语

水工钢闸门轨道特殊的受力和边界条件，是轨道弯曲应力分布异于初等梁情况的原因。轨道与混凝土基础的水平摩阻力使轨道底面弯曲应力有较大幅度下降，轮轨接触局部荷载的作用与弯矩的叠加效应使轨道顶面弯曲应力有大幅度提高，本文的式（10）和（14）可分别用于计算轨道底面和顶面的最大弯曲应力。本文的分析很好地解释了三峡水利枢纽高压闸门定轮支承结构试验中轨道弯曲应力测试中的试验现象。

［1］ 河海大学.三峡水利枢纽高压闸门定轮支承结构试验研究［R］.南京：河海大学，2001.

［2］ SL74-95，水利水电工程钢闸门设计规范［S］.

［3］ 雷声昂，和秀芬.安各庄水库溢洪道闸门主轮轮轨强度的新探讨［J］.河北水利水电技术，1995，（4）：23-25.

［4］ 日本闸门钢管协会.闸门钢管技术标准（第四次修订版）［S］.1993.

［5］ 西德工业标准19704.水工钢结构物的计算基础［S］.1976.

［6］ 谈至明.具有水平摩阻力的弹性地基上梁的解［J］.力学与实践，1997，19（3）：33-35.

［7］ GB50017-2003，钢结构设计规范［S］.

［8］ 中国船舶工业总公司第九设计研究院.弹性地基梁及矩形板计算［M］.北京：国防工业出版社，1983.

［9］ JOHSON K L.接触力学［M］.徐秉业，罗学富，译.北京：高等教育出版社，1992.

（编辑：周晓雁）

Bending Stress of Cross-section in Track of Hydraulic Steel Gate

BAIRun-bo1，2，CAO Ping-zhou1，QIU Li-qing1
（1.College of Civil Engineering，Hohai University，Nanjing 210098，China；2.College of Hydraulic and Civil Engineering，Shandong Agricultural University，Tai'an 271018，China）

Themeasured values of the longitudinal stress in the full size hydraulic track testmodel are differentfrom the values calculated by the Chinese applicable codes.This problem is studied by use of the theoretical derivation，numerical calculation and FEM.Studies indicate that the particular boundary conditions and forces exerted on the hydraulic track are themain reason of the normal stress of cross-section in track being different from the general beam theory.The bending stress of bottom of the track appears a biggest-range descent due to horizontal resistance between track and concrete foundation.And the normal stress of cross-section in the top of the track occurs a wide-range ascent due to the superimposed effect of local load of wheel-track contact and bending moment.The formulas proposed in this article can be used for structures design.This analysis can well explain the phenomenon occurring in the testof bending stress of track which is the supporting structure of fixed-roller wheel high-pressure gate of TGP.

steel gate；track；bending stress；friction；local stress

TV34

A

1001-5485（2009）08-0068-05

2008-11-03；

2008-12-16

江苏省研究生培养创新工程（CX07B_129z）；山东省教育厅资助项目（J07YE04-32426）

白润波（1982-），男，山东泰安人，博士研究生，主要从事金属结构研究，（电话）025-83789970（电子信箱）bai1982＠126.com。