上海地区③土层上无桩基础水闸实测沉降资料分析

付新永，杜占鹏，姚顺雨，徐 兵

（1.上海青草沙投资建设发展有限公司，上海 201206；2.浙江省第一水电建设集团有限公司，杭州 310051；3.上海勘测设计研究院科研所，上海 200434）

上海地区③土层上无桩基础水闸实测沉降资料分析

付新永1，杜占鹏2，姚顺雨3，徐 兵3

（1.上海青草沙投资建设发展有限公司，上海 201206；2.浙江省第一水电建设集团有限公司，杭州 310051；3.上海勘测设计研究院科研所，上海 200434）

基于上海地区③土层上的一座无桩基础水闸——祝家港节制闸闸室的沉降资料，分别对沉降曲线本身、用双曲线配合法对地基土的最终沉降量进行预测及地基土沉降与地基反力的关系这3个方面进行了分析。分析结果表明：上海地区③土层上无桩基水闸施工期的沉降量一般在-40 mm左右，沉降曲线在水闸通水后一般都经历一个月的“假收敛期”；从用双曲线配合法推求的地基最终沉降量预测值来看，施工期③土层的瞬时沉降（弹／弹塑性变形）sd占最终沉降量的比例为25%～50%，S∞后续的大部分沉降都要在竣工后的长期使用期间内再发生；结合地基反力的测试结果来看，③土层地基反力与变形相互协调变化。

上海地区；③土层；无桩基础水闸；闸室；实测沉降

沉降分析是土力学的基本课题之一，对于软黏土地基上的建筑物，必须控制其沉降量和不均匀沉降差。沉降量大小主要取决于使土体产生变形的原因和土体本身性状两个方面。经典的沉降计算方法对于这两个方面是这样处理的：在荷载作用下地基附加应力场是根据半无限空间各向弹性体理论来计算的，土体压缩性是根据一维压缩试验来测定的，并采用分层总和法来计算建筑物的沉降［1］。

第二类计算方法为近年来发展起来的数值计算方法，即根据固结理论，结合各种土体的本构模型，计算最终沉降量及其发展规律［2］。

显然，上述2种沉降计算模型与地基沉降的真实性存在不少的差距。因为2类方法计算公式中的参数必须通过试验方法获得，而土体取样不可避免地会对原状土产生扰动，从而也就不可避免地给需要测定的参数带来误差，导致理论方法计算出来的变形量及变形规律与土体的实际变形量及变形规律不一定相符合。

通过现场实测资料来分析和估算沉降量与时间关系可以避免由室内土工试验所带来的参数测定的误差，显示出独有的优势。

本文以座落在上海地区③土层上无桩基础的一座节制闸闸室的沉降观测资料来作分析与讨论。

1 工程概述

祝家港节制闸工程位于上海市松江区境内，为一座14 m宽的单孔节制闸。水闸座落在③土层上，依据《祝家港节制闸工程地质勘察报告》［3］：节制闸建基面高程-2.30 m，底板尺寸16.0 m×16.0 m，底板最大地基反力为80 kPa，地基土允许承载力为120.0 kPa，依据分层总和法计算水闸天然基础下的最终沉降量为12.0 cm。显然，报告中地基允许承载力和最终沉降量均满足《水闸设计规范》［4］要求。

在该水闸的底板四角各布置1个沉降测点，在水闸的底板下共埋设YUB-2型差动电阻式土压计5只。依据监测资料，通水前埋设在底板齿坎内的3只土压力测值均已超过120.0 kPa，最大值已达147.8 kPa，实测地基应力不均匀系数为2.67，通水后土压计测值均已超过120.0 kPa，最大值达203.0 kPa，实测地基应力不均匀系数为2.05。测试结果表明测值较大的土压计出现在墩墙角点部位。显然，地基反力已超过设计时的地基土允许承载力的要求。

2 土层物理力学性质

各土层的物理力学性质见表1。从表1可以看出：③，④，⑤土层均为高压缩性饱和土层，③土层呈软塑-流塑状态，④，⑤土层呈流塑状态。

闸址区为河网低地，靠近黄浦江，地下水主要接受大气降水补给，向河网排泄，另外，黄浦江的潮位变动也影响地下水位。地下水位的稳定水位埋深为0.70～2.30 m。

表1 地基土物理力学性质统计表Table1 Physical-mechanical parameters of foundation soil

室内试验测得③土层的水平渗透系数为9.68× 10-6cm／s，垂直渗透系数为4.37×10-6cm／s。

3 闸室沉降现场监测成果及分析

节制闸沉降测点及土压计的布置见图1。

图1 闸室部位土压计及沉降测点布置图Fig.1 Arrangement ofmeasured settlement points＆earth pressure cells for regulator chamber position

3.1 闸室沉降现场监测

节制闸底板浇筑完成后，即开始在底板的四角布置沉降测点进行观测。节制闸闸室的沉降过程线见图2。

图2 闸室沉降历时过程线Fig.2 Observed duration curves of settlement for the regulator chamber

从图2来看：①监测末期的底板沉降曲线已趋于收敛，底板最大沉降量约-40 mm（LD6），最小沉降量约-27 mm（LD2），差异沉降数值约为4～13 mm。显然，实测沉降量未超过《水闸设计规范》［4］中关于“天然土质地基上水闸地基”最大沉降量和相邻部位最大沉降差的要求，也未到达《祝家港节制闸工程地质勘察报告》［3］中用分层总和法计算出的结果。②监测末期底板西侧的沉降量明显大于东侧的沉降量，水闸底板出现了一定程度的倾斜，底板最大倾斜度约为1.07 mm／m。由于启闭机房在闸室正上方部位，可以认为上部荷载基本均匀，由此可认为差异沉降主要是由于地基土的不均匀所致。③从监测结果来看，尽管③土层属饱水淤泥质软塑性黏土层，但作浅基的持力层时，实测最终沉降量数值基本在-40 mm以内，且沉降曲线收敛较快。而且在水闸实现通水后，沉降曲线都经历了一个月左右的“假收敛期”，但当该时段过后，曲线随即出现斜率突然增大且很快又趋于收敛的情形，该情形与祝家港节制闸相邻的水工建筑物类似，一座为紫石泾节制闸，一座为紫石泾套闸（2座闸室），底板都座落在③2层无桩基天然土质地基上。这个现象可能主要与渗透系数有关。③土层的渗透系数为10-6数量级，属于典型的弱透水层。也就是说，在水闸刚实现通水的一个月内，水并未充分渗透通③土层，土体仍处于非饱和状态，所以水土合力并未出现大的增长。水经过一个月左右的时间在③土层中缓慢渗透，当土体达到饱和状态后，水土合力快速增长，地基应力不均匀系数减小，水对地基土的性状改变发生作用，地基土土性改变的效应才发挥出来。这一点从图3中可以得到印证。

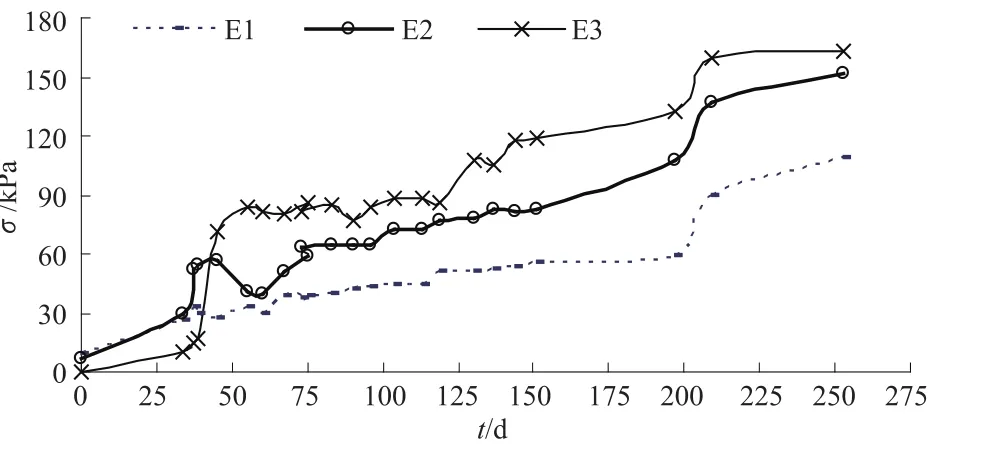
图3 闸室地基反力历时过程线Fig.3 Observed duration curves of reactive forces for the regulator chamber

3.2 ③土层最终沉降量的预测

采用现场实测沉降资料来推算总沉降量时，曾国熙（1985）建议地基固结度用公式U＝1-αe-βt来进行计算，从而推演出“三点法”求最终沉降量的估算公式；Makasa导出Asaoka法利用已有的实测沉降资料预估总沉降，还有双曲线配合法、指数曲线配合法等。无论哪种估算方法，基本的思路都是依据初期的观测资料通过反分析法得到地基土的参数，然后通过正分析法得到最终沉降量［1］。对于高压缩性软黏土，其应力应变关系明显呈非线性，魏汝龙［5］认为软黏土压缩曲线整个形状更符合双曲线型，因此，本文用双曲线配合法推求地基土的最终沉降量，经验公式为

式中：St为t时的沉降量（mm）；S0为初期沉降量（mm）；t为实测沉降历时（d）；α，β为待定经验参数。

当t→∞时，各测点最终沉降量S∞可由下式推算，即

应用公式（1）和（2）时取荷载完全施加后开始计算水闸通水后“假收敛期”的末次测值为S0，即第183天测值，以第187天测值和第189天测值推算值β和S∞，由此估算出的地基最终沉降量S∞在80～100 mm之间，计算出的β值及S∞见表2。

表2 计算出的β值及S∞统计表Table 2 β＆S∞of calculated data

本工程施工期的瞬时沉降（弹／弹塑性变形）Sd（按8个月～1年考虑）为-25～-40 mm，占S∞的比例为25%～50%，后续的大部分沉降，都要在竣工后的长期使用期间内再发生。

3.3 地基反力与地基土沉降分析

从图2来看，监测末期测点LD1的沉降量略大于测点LD6；从图3来看，沉降测点LD1处的土压计E4测值也略大于沉降测点LD6处的土压计E1的测值，地基反力分布的不均匀从而也导致了地基土沉降的不均匀。相反地，地基土沉降的不均匀也会导致地基反力分布的不均匀，由于水闸底板为刚性底板，所以水闸底板中间位置的土压计E3测值介于E1和E4之间。当地基土的沉降趋于收敛时，土压计测值也基本趋于收敛，变形与土压力测值处于不断协调变化。

4 结 论

（1）上海地区③土层上无桩基础水闸施工期沉降量一般在-40mm左右趋于收敛，并且由于是弱透水层，沉降曲线在水闸实现通水后会经历一个月左右的“假收敛期”。主要是③土层中渗透系数较小，水在其中缓慢渗透，当地基土达到饱和后，地基性状发生改变所致。

（2）用双曲线配合法推求③土层地基土的最终沉降量结果表明，施工期的瞬时沉降（弹／弹塑性变形）Sd（按8个月至1年考虑）占S∞的比例为25%～50%，后续的大部分沉降，都要在竣工后的长期使用期间内再发生。

（3）结合地基反力过程线和沉降曲线来看，③土层变形与地基反力相互协调变化。

［1］ 龚晓南.高等土力学［M］.杭州：浙江大学出版社，1998.

［2］ 潘林有，谢新宇.用曲线拟和的方法预测软土地基沉降［J］.岩土力学，2004，25（7）：1053-1058.

［3］ 蒋天纵.祝家港节制闸工程地质勘察报告［R］.上海：上海勘测设计研究院勘测公司，2002.

［4］ SL265-2001，水闸设计规范［S］.

［5］ 魏汝龙.从实测沉降过程推算固结系数［J］.岩土工程学报，1993，15（2）：12-19.

（编辑：赵卫兵）

Analysis on In-situ Settlement Measurement of Sluice without Piles Located on③Soil Stratum in Shanghai

FU Xing-yong1，DU Zhan-peng2，YAO Shun-yu1，XU Bing3
（1.Shanghai Qingcaosha Investment Construction＆Development Co.，ltd.，Shanghai 201206，China；2.Zhejiang Provincial No.1Water Conservancy＆Electric Power Construction Group CO.，Lcd.，Hangzhou 310051，China；3.Science＆Research Department of Shanghai Investigation，Design＆Research Institute Shanghai，Shanghai 200434，China）

On the basis of themeasured displacements from the chamber of a check sluice in Zhujia Harbor，

the total settlements obtained from the time-settlement curve and hyperbolic matchingmethod were compared.The relationship between displacement and foundation resistance was analyzed.The check sluice was built directly on the 3rdstratum of Shanghai claywith no piles underneath.The results showed that：（1）the sluice settlement during construction period was about-40 mm；（2）a typical pseudo-convergence would occur on the time-settlement curve during the firstmonth after the sluice running；（3）the settlement data predicted by the hyperbolicmatching method indicated the transient（elastic／elastoplastic）settlementwas about 25%-50%of the total settlement，of which the restwill appear again in a long time after construction；（4）themeasured resistance in the 3rdstratum of Shanghai clay was concordantwith themeasured displacement.

Shanghai；third stratum of soil；sluice without piles；chamber；in-situ settlementmeasurement

TV223.2

A

1001-5485（2009）08-0051-03

2008-10-09

付新永（1972-），男，上海市人，工程师，主要从事工程建设管理工作，（电话）021-66858619（电子信箱）gcsfxy＠126.com。