案例研究——牛鞭效应的系统动力学分析
2009-07-24赵军刘飞
赵 军 刘 飞
摘要:利用系统动力学的方法和仿真软件Vensim,对Y公司K产品的供应链上的牛鞭效应进行了建模与仿真。针对该供应链上牛鞭效应显著的实际情况,提出了缩短订单延迟时间,延长库存调节时间,采用供应商管理库存的综合解决方案,仿真结果表明该解决方案能在一定程度上减轻牛鞭效应的影响,研究结果可为Y公司的实际生产组织提供决策依据。
关键词:系统动力学;供应链;牛鞭效应;仿真;供应商管理库存
中图分类号:F273.7文献标识码:A
Abstract: This paper adopts the system dynamics and its simulation software Vensim to modeling and simulating the bullwhip effect in the supply chain of the Y company's k product. Based on the reality situation of the bullwhip effect in this supply chain, it brought forward shortening delay time of order, prolonging adjust time of inventory, adopting vendor managed inventory to solve this problem, the simulation results proved that these method could alleviate the effect of the bullwhip effect in some extend, the research results could enrich the decision about the reality product organization for company Y.
Key words: system dynamics; supply chain; bullwhip effect; simulation; vendor managed inventory
牛鞭效应指供应链中需求信息从下游企业向上游企业传递时,信息被扭曲并逐级放大的现象[1]。系统动力学出现于1956年, 该方法在20世纪50年代后期主要被用于企业管理,解决诸如原材料供应、生产、库存、销售、市场等一系列问题[1]。刘媛媛等[2]应用系统动力学研究了供应链节点变化对牛鞭效应的影响,利用系统动力学专用软件VENSIM,对“啤酒游戏”进行仿真分析,研究当供应链上节点增加时“牛鞭效应”的变化情况;李稳安等[3]用系统动力学原理研究了供应链中牛鞭效应产生的原因及相应的缓解对策,建立了多节点供应链系统的动力学模型,给出了系统动力学的迭代表达式和框图,并定性地说明了牛鞭效应产生的内在机理;王磊等[4]对研究牛鞭效应时经常讨论到的三种模型:系统动力学模型、自回归分析的AR(1)模型和Kalman滤波器(KF)模型进行了分析和比较。杨诗华[5]在其硕士论文中基于系统动力学原理,应用Powersim仿真软件对啤酒分销模型的三级供应链中牛鞭效应现象进行了仿真设计,提出缓解牛鞭效应的对策;苗兴东[6]在其硕士论文中采用系统动力学研究牛鞭效应的机理,利用系统动力学专用软件VENSIM,首先研究极端情况下的牛鞭效应(包括曲线和数据计算),然后通过调整参数来减弱牛鞭效应,从而得出结论。本文以一家生产化妆品系列的外贸出口企业Y公司为背景,首先运用系统动力学的方法对该公司K产品供应链上的牛鞭效应进行建模,其次应用系统动力学仿真软件Vensim PLE 5.4b对该牛鞭效益进行模拟仿真,最后针对该公司K产品的供应链上存在的问题,提出改进措施,以减轻牛鞭效应的影响。
1Y公司介绍
Y公司是一家生产化妆品系列的外贸出口型企业,主要承接英国、法国及美国等国家的生产订单,按照客户的要求进行生产。其产品品种多,颜色丰富,款式也非常多,甚至曾经生产过的某些产品,其款式无一相同。Y公司K产品的供应链由消费者c,零售商d、批发商W和Y公司所组成。该供应链上的参加人员各自扮演不同角色,且完全独立地做出决策,他们唯一的目标是使各自决策的利润最大化,即各个物流环节的订货策略都是:Qij=SIij-Iij/Ti+Nj,其中:Qij, SIij, Iij分别为第i个物流环节第j周的订货量、安全库存量和期末库存量(在缺货情况下取值为0);Ti为第i个物流环节库存的调节时间;Nj为第j周期下游物流单元的需求量。已知消费者的需求是一个阶跃函数,第一周市场需求率是4件/周,从第二周开始每周市场需求率都是8件/周。零售商的安全库存量为12件,库存调节时间为4周,期末库存量初始值为12件,累计缺货量初始值为0件,与消费者间没有时间延迟。批发商的安全库存量为12件,库存调节时间为4周,期末库存量初始值为12件,累计缺货量初始值为0件,与零售商间有4周的时间延迟。制造商的安全库存量为12件,库存调节时间为4周,期末库存量初始值为12件,累计缺货量初始值为0件,与批发商商间有4周的时间延迟,生产有2周的时间延迟。
2系统动力学建模与仿真
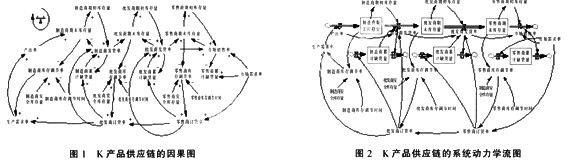
2.1K产品供应链的因果图
在K产品的供应链中,有三个物流单元,包括:制造商Y公司、批发商w、零售商d,而各个物流单元之间用通讯和运输相联系。根据各个环节的关系,画出K产品供应链的因果关系图,如图1所示。
2.2K产品供应链的系统动力学流图
根据图1的因果关系图,可进一步得出K产品供应链的系统动力学流图,如图2所示。这里确定六个水平变量:制造商期末库存量,批发商期末库存量,零售商期末库存量,制造商累计缺货量,批发商累计缺货量,零售商累计缺货量;八个速率变量:制造商的产出率,制造商生产需求率,制造商发货率,批发商订货率,批发商发货率,零售商订货率,市场销售率,市场需求率。
2.3K产品供应链的系统动力学模型
制造商产出率是其生产需求率的一阶延迟,制造商的发货率是批发商订货率的三阶延迟,批发商的发货率是零售商订货率的三阶延迟。K产品供应链的系统动力学模型具体如下:(1)零售商安全库存量=12件;(2)零售商库存调节时间=4周;(3)零售商库存调节率=(零售商安全库存量-零售商期末库存量)/零售商库存调节时间,件/周;(4)零售商期末库存量=INTEG(DELAY3(批发商发货率,4)-市场销售率,12),件;(5)零售商期初库存量=DELAY3(零售商期末库存量, 1),件;(6)零售商累计缺货量=INTEG(市场需求率-市场销售率,0),件;(7)零售商订货率=零售商库存调节率+市场需求率,件/周;(8)市场需求率=4+STEP(4 , 2),件/周;(9)市场销售率=MIN(零售商期初库存量+DELAY3(批发商发货率,4),市场需求率),件/周;(10)批发商安全库存量=12件;(11)批发商库存调节时间=4周;(12)批发商库存调节率=(批发商安全库存量-批发商期末库存量)/批发商库存调节时间,件/周;(13)批发商期末库存量=INTEG(DELAY3(制造商发货率, 4)-批发商发货率,12),件;(14)批发商期初库存量=DELAY3(批发商期末库存量, 1),件;(15)批发商累计缺货量=INTEG (DELAY3(零售商订货率, 4)-批发商发货率,0),件;(16)批发商订货率=DELAY3(零售商订货率, 4)+批发商库存调节率,件/周;(17)批发商发货率=MIN(批发商期初库存量+DELAY3(制造商发货率, 4), DELAY3(零售商订货率, 4)+DELAY3(批发商累计缺货量, 1)),件/周;(18)制造商安全库存量=12件;(19)制造商库存调节时间=4周;(20)制造商库存调节率=(制造商安全库存量-制造商期末库存量)/制造商库存调节时间,件/周;(21)制造商期末库存量=INTEG(产出率-制造商发货率,12),件;(22)制造商期初库存量=DELAY3(制造商期末库存量, 1),件;(23)制造商累计缺货量=INTEG(DELAY3(批发商订货率, 4)-制造商发货率,0),件;(24)生产需求率=DELAY3(批发商订货率, 4)+制造商库存调节率,件/周;(25)制造商发货率=MIN(制造商期初库存量+产出率, DELAY3(批发商订货率, 4)+DELAY3(制造商累计缺货量, 1)),件/周;(26)产出率=DELAY3(生产需求率, 2),件/周。
2.4Vensim系统动力学仿真
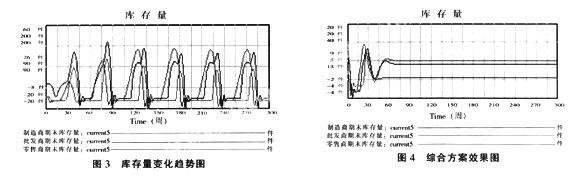
本仿真的时间范围是0~300周, 步长为0.125,在Vensim PLE 5.4b版本上仿真运行该模型,各个物流环节期末库存量变化趋势如图3所示。从图3中我们可以看出,由于K产品供应链上各个环节各自为政,库存调节时间较短,订单延迟时间较长,导致了该条供应链上牛鞭效应显著,这与Y公司K产品现阶段供应链实际情况相符合。
2.5解决方案
这里我们综合采用缩短订单延迟时间,延长库存调节时间,采用供应商管理库存的解决办法。现阶段K产品供应链上,制造商产出率是其生产需求率的一阶延迟,制造商的发货率是批发商订货率的三阶延迟,批发商的发货率是零售商订货率的三阶延迟,全都改进为一阶延迟;各物流环节库存调整时间为4天,全都改进为延长8天;采用供应商管理库存的解决方案。各个物流环节的订货策略改变为:Qij=SEij-Iij/Ti+Nj,SEij为期望库存量,对下一环节需求率做一次指数平滑预测。变化的系统动力学模型为:(1)零售商期望库存量=SMOOTHI(市场需求率, 1, 零售商平滑系数),件;(2)零售商库存调节率=(零售商期望库存量-零售商期末库存量)/零售商库存调节时间,件/周;(3)批发商期望库存量=SMOOTHI(零售商订货率, 1, 批发商平滑系数),单位:件;(4)批发商库存调节率=(批发商期望库存量-批发商期末库存量)/批发商库存调节时间,件/周;(5)制造商期望库存量=SMOOTHI(批发商订货率, 1, 制造商平滑系数),件。平滑系数取为0.1;(6)制造商库存调节率=(制造商期望库存量-制造商期末库存量)/制造商库存调节时间,件/周。原模型中去掉零售商、批发商、制造商安全库存量的方程,其他不变。改进后效果如图4所示。
3结论与评价
本文利用系统动力学建模,在系统动力学仿真软件Vensim PLE 5.4b版本上进行仿真,主要得到以下结论:(1)图3表明:由于订单延迟时间较长,库存调节时间较短,采用传统库存管理办法,Y公司K产品供应链上每个物流环节各自为证,牛鞭效应显著;(2)从图4中我们可以看出,综合利用三种解决方案,可以得到显著的效果,系统在60周左右处于完全平衡状态,与单靠缩短延迟时间相比,提前了30周的时间。本文针对Y公司K产品的供应链上牛鞭效应显著的情况,进行了定性分析,并给出可行的综合解决方案,然而延迟时间缩短为多少,库存调节时间延长为多少,供应商管理库存有许多方法,对下游物流环节需求的预测,对库存的调节率都有相当多的理论与方法,怎样保证改进方案既经济又可行,还需具体问题具体分析,这些都是本文值得进一步研究的地方。
参考文献:
[1]彭扬, 伍蓓. 物流系统优化与仿真[M]. 北京: 中国物质出版社, 2007.
[2]刘媛媛, 王海燕. 供应链节点变化对牛鞭效应影响的系统动力学仿真研究[J]. 物流技术, 2006,25(6):50-53.
[3]李稳安, 赵林度. 牛鞭效应的系统动力学分析[J]. 东南大学学报: 哲学社会科学版, 2002,33(10):96-98.
[4]王磊, 陈竞先, 唐志. 供应链中牛鞭效应的模型与分析[J]. 物流技术, 2004,10(1):42-46.
[5]杨诗华. 供应链管理中牛鞭效应机理分析与仿真[D]. 哈尔滨: 哈尔滨工业大学, 2006.
[6]苗兴东. 系统动力学在供应链建模中的应用[D]. 成都: 西南交通大学, 2006.
