利用远场模式的不完全数据反演声波阻尼系数

麦宏晏,王连堂

(1.长安大学理学院,陕西西安 710064;2.西北大学数学系,陕西西安 710069)

利用远场模式的不完全数据反演声波
阻尼系数

麦宏晏1,王连堂2

(1.长安大学理学院,陕西西安 710064;2.西北大学数学系,陕西西安 710069)

从阻尼边界条件声波散射问题的散射场远场模式的部分数据信息出发给出了反演声波阻尼系数的一种新方法,该问题既是非线性的又是不适定的,这里利用Tikhonov正则化方法将问题转化为一个最优化问题,成功地处理了第一类算子方程的不适定性及该问题的非线性性,给出了具体的数值方法并对其收敛性进行了严格地证明,数值结果表明该方法是非常准确且简单易行的.

阻尼边界条件;远场模式;反演;部分数据

1 引言

文[1-4,6,9]给出一些利用远场模式的完全或不完全数据反演声波阻尼系数和阻尼区域的结果.本文给出一种比文[4]更加简单易行的方法.

考虑在各向同性的介质D⊂R2中传播的声波,令D是有界的单连通区域,∂D是C2类的且取入射场为ui(x)=exp[ikx·α],其中k＞0是波数,α是单位向量.散射场记为us,全场记为u=ui+us,于是阻尼边界条件的声波正散射问题归结为求u∈C2(R2)∩C(R2D),满足

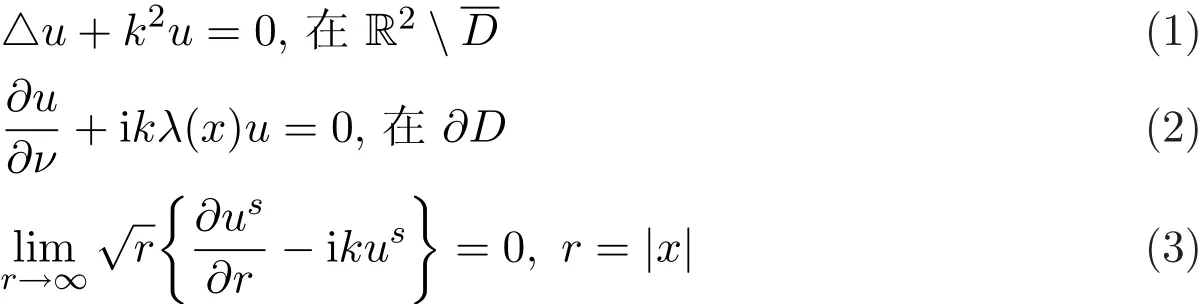
其中ν表示单位外法向量,λ(x)∈C(∂D)是阻尼系数.

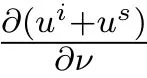
2 反演方法

假定k2在∂D内部不是负的Lapacian算子的Dirichlet特征值,例如可以选择∂D是半径为R的圆且kR不是球Bessel函数jn的零点,n=0,1,2,…,由文[8],利用单层位势

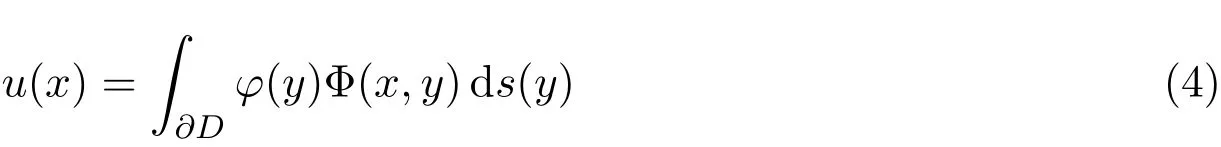
2 收敛性分析

4 数值算例

下面我们给出具体的算法描述,为了获得更准确的反演结果,取入射波为

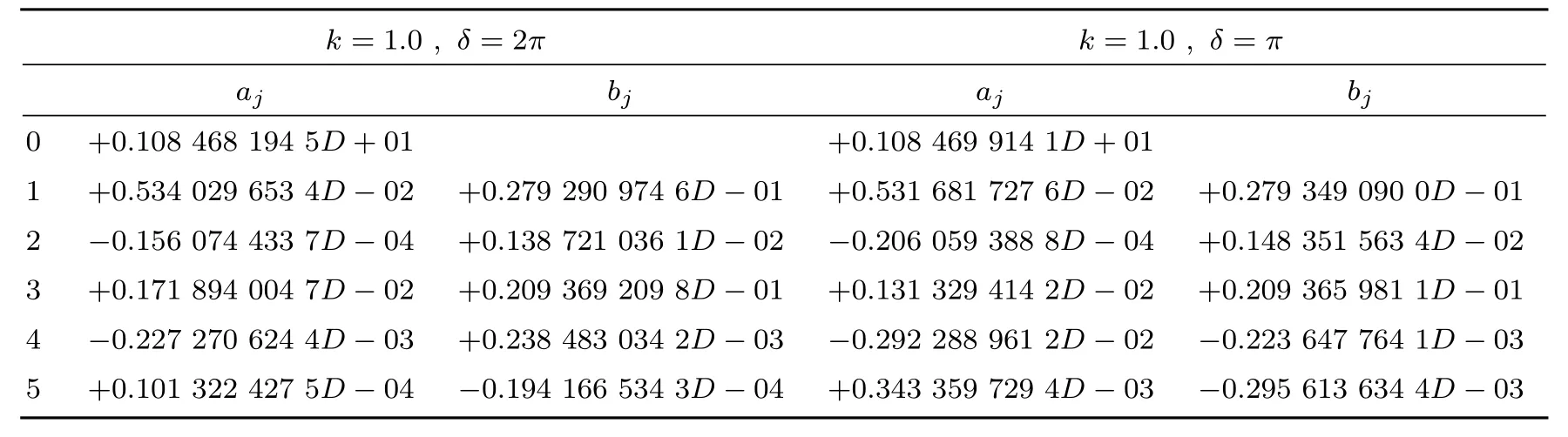
表1 例1的反演结果

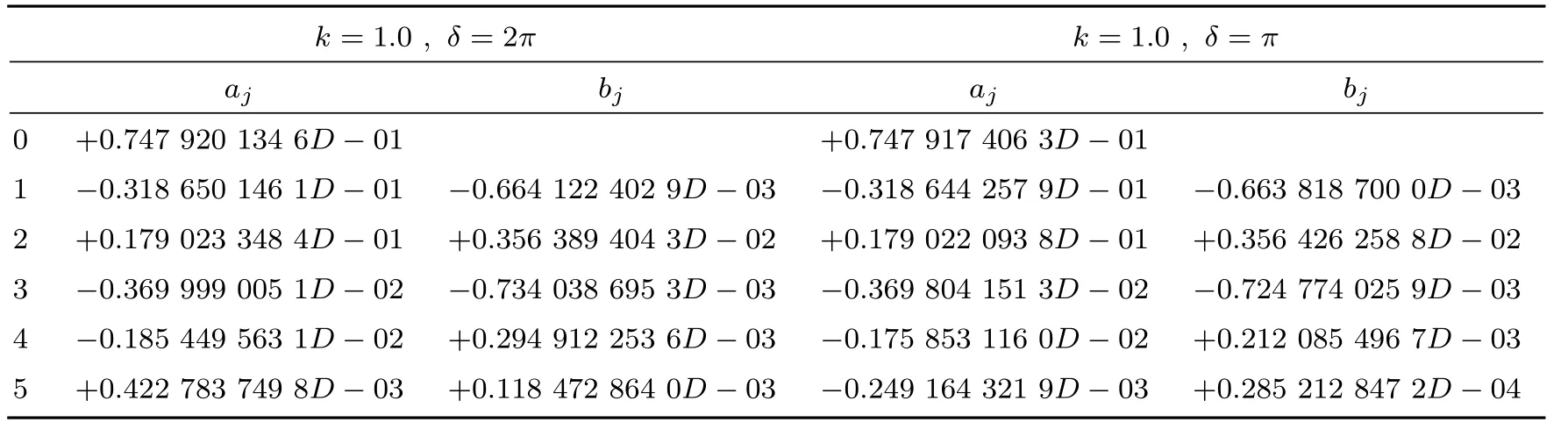
表2 例2的反演结果

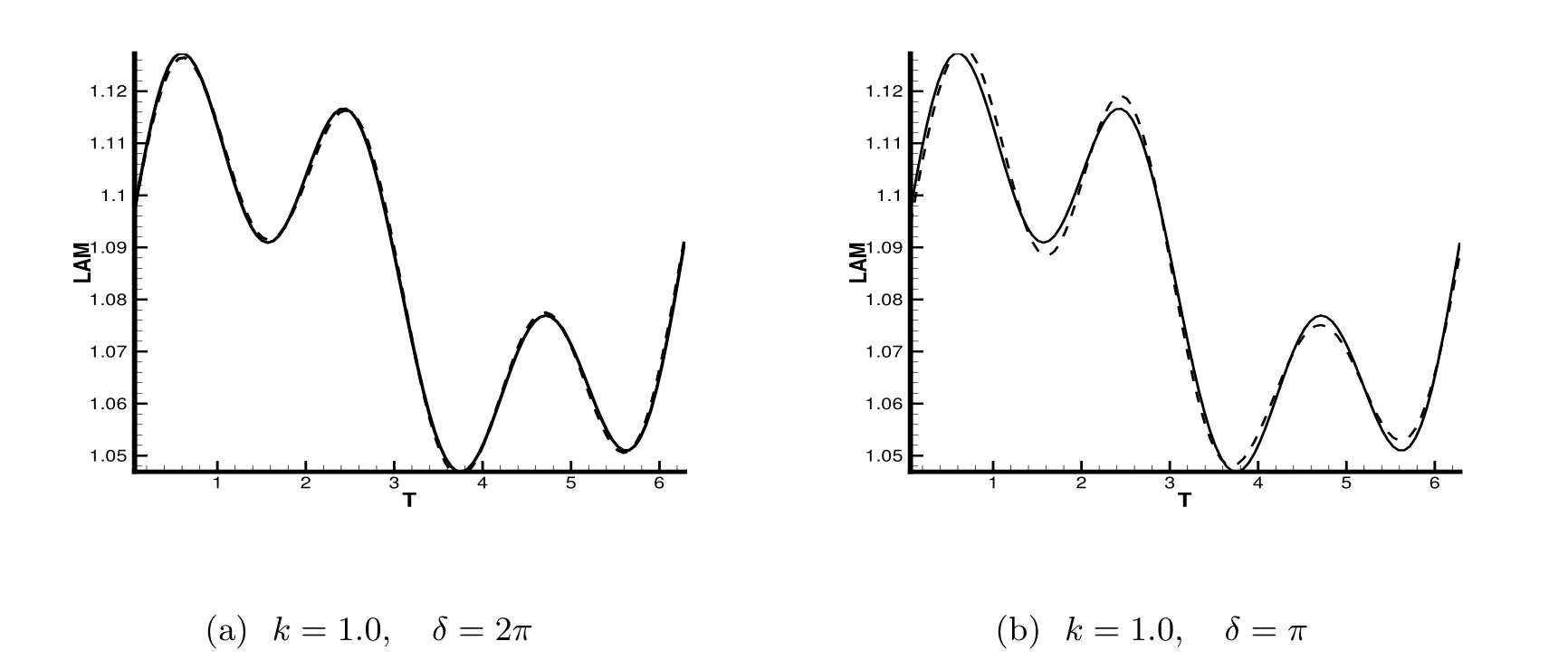
图1 λ(x)=的准确结果及反演结果

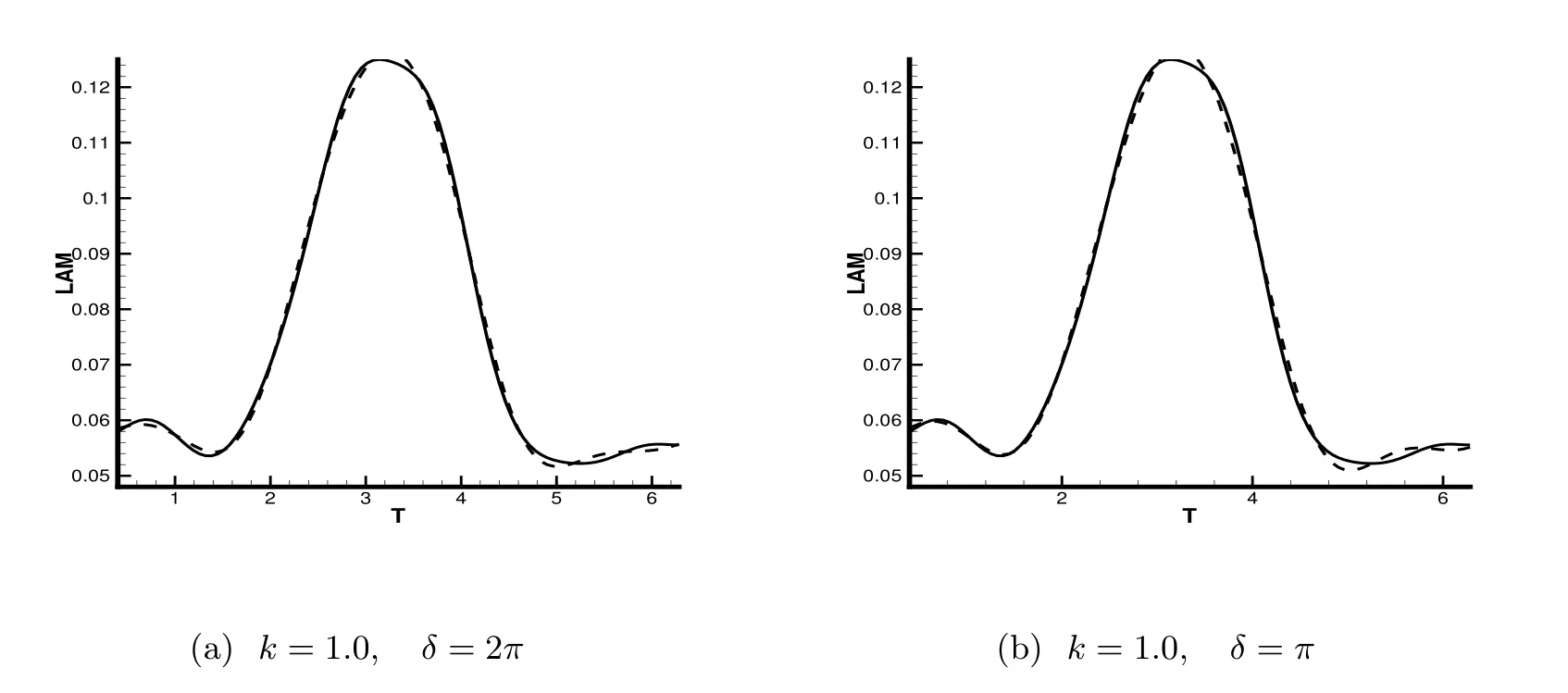
图2 λ(x)=的准确结果及反演结果

这里正问题的参数n选取的越大,正问题计算精度越高,由此反演结果也会越好；不过参数n选取的过大,不仅增加了正问题的计算量,更是大大增加了反问题的计算量,从而使反问题的计算速度大大降低.参数N用来表示入射方向的个数,反演声波阻尼系数和区域时,该参数取的太小不能反映真实情况,取的太大又增加了计算量.参数n1,n2与阻尼系数的逼近有关,取的越大,反演结果越准确,当然也会相应地增加计算量.综合计算量和计算精度的考虑,同时参阅文[7]给出的误差分析,本文参数的选取是合适的.

由上面的算例还看出由完全数据反演的结果比部分数据反演的结果要好,当δ取的较大时反演结果较好.

[1]Colton D,Monk P.A novel method for solving the inverse scattering problem for time-harmonic acoustic waves in the resonance region[J].SIAM J.Appl.Math.,1985,45:1039-1053.

[2]Colton D,Monk P.A novel method for solving the inverse scattering problem for time-harmonic acoustic waves in the resonance region II[J].SIAM J.Appl.Math.,1986,46:506-523.

[3]王连堂.反演声波阻尼系数的一个逼近方法[J].计算数学,2000,22(3):265-274.

[4]王连堂,何志强.利用远场模式的不完全数据反演声波阻尼系数[J].计算数学,2003,25(2):245-256.

[5]Kitsch A,Kress R.An optimization method in inverse acoustic scattering[M]//Boundary Elements IX vol 3 Fluid Flow and Potential Applications.New York:Springer-Verlag Berlin Heidelberg,1987,3.

[6]Ochs R L.The limited aperture problem of inverse acoustic scattering:Dirichlet Bounary Contions[J].SIAM J.Appl.Math.,1987,47:1320-1941.

[7]Colton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory[M].New York:Springer-Verlag, 1992.

[8]Colton D,Kress R.Integral Equation Methods in Scattering Theory[M].New York:Wiley-Interscience Publication,1983.

[9]王枢,孟文辉.利用远场模式的完全与不完全数据反演声波阻尼区域[J].纯粹数学与应用数学,2006,22(1): 99-107.

Recovering the acoustic wave impedance coefficient from the incomplete far field pattern data

MAI Hong-yan1,WANG Lian-tang2
(1.The School of Science,Chang’an University,Xi’an710064,China; 2.Department of Mathematics,Northwest University,Xi’an710069,China)

The method we are considering in this article is a novel method to recover the impedance coefficient from the knowledge of the incomplete far field pattern data of the scattered wave for the time-hormonic acoustic scattering problem.It is transformed into an optimization problem employing Tikhonov regularization method in order to solve the ill-posedness of the equation of the first kind and its nonlinearity successfully.Numerical method is given and the convergence of the method is rigorously proven.Numerical examples are shown that this method is both accurate and simple to use.

impedance boundary condition,far field pattern,recover,incomplete data

O175.29

A

1008-5513(2009)03-0566-07

2008-02-27.

长安大学科技发展基金(07J05).

麦宏晏(1972-),讲师,研究方向：数学物理方程反问题.

2000MSC:31A25