正规密码H#-富足半群的结构

陈益智,邵勇

(1.广东惠州学院数学系,广东惠州 516007;2.西北大学数学系,陕西西安 710127)

正规密码H#-富足半群的结构

陈益智1,2,邵勇2

(1.广东惠州学院数学系,广东惠州 516007;2.西北大学数学系,陕西西安 710127)

证明了H#-富足半群S是正规密码H#-富足半群当且仅当它是完全J#-单半群的强半格.该结果也是正规密码超富足半群和正规密码群并半群分别在超富足半群和完全正则半群上的相应结构定理的推广.

#-格林关系;正规密码H#-富足半群;完全J#-单半群;强半格

1 引言

文[1-2]中,作者引入了格林∗-关系.它的等价表述如下[3]:设S是半群

其中,J∗(a)和J∗(b)分别是由a和b生成的主∗-理想.

文[3]中,作者研究了富足半群,这类半群的每个L∗-类和每个R∗-类都包含了至少一个幂等元.此外,作者还给出了超富足半群的概念,即每个H∗-类都包含有一幂等元的半群称为是超富足半群.容易看出,富足半群、超富足半群分别是正则半群和完全正则半群的真推广.此外,文[4]中系统地研究了超富足半群的结构,推广了文[5]中的关于完全正则半群结构的相应结果,并完善了文[3]中关于超富足半群的相关结论.

由文[3]知道,如果半群S的每个幂等元都是本原的,那么S就被称为是本原的;如果富足半群S是本原的,并且S的幂等元生成一个正则子半群,则S称为是完全J∗-单半群;S是完全J∗-单半群也等价于S是超富足半群并且是J∗-单的.显然,完全J∗-单半群是由Clifford和Petrich在文[6]所研究的完全单半群的推广.

最近,文[7]定义了一类新的格林关系:#-格林关系.即

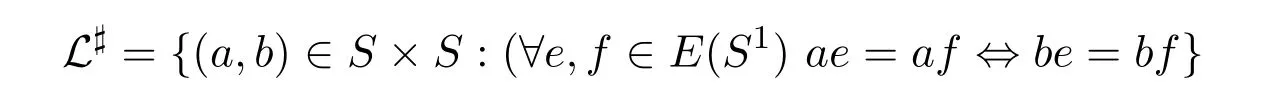
由文[8]可知,超富足半群S是正规密码超富足半群当且仅当它是完全J∗-单半群的强半格.同时,注意到H#-富足半群是超富足半群的推广,完全J#-单半群是完全J∗-单半群的推广,于是,自然地我们会考虑这样的问题:正规密码H#-富足半群是否与完全J#-单半群的强半格等价?

本文就上面提出的问题进行了研究探讨,且证明给出:半群S是正规密码H#-富足半群当且仅当它是完全J#-单半群的强半格.该结果也是正规密码超富足半群和正规密码半群在超富足半群和完全正则半群上的相应结构定理的推广.

为了给出本文主要结果,首先引进了#-富足半群上的自然偏序,然后探讨了H#-富足半群的若干性质和特征,最后证明了正规密码H#-富足半群的主要结构定理,同时还对其两类特殊情形进行了探讨.

对于本文未提及的概念和术语,读者可参看文[7,9-11].

2 #-富足半群上的自然偏序

本节将主要引进#-富足半群上的自然偏序的概念.

证明我们只需证L#(xa)⊆L#(a)即可.显然,xa∈S1a,其中S1a是包含a的最小左理想.由于L#(a)是一个包含a的左理想,故有S1a⊆L#(a),从而xa∈L#(a).另一方面,因为L#(xa)是包含xa的最小左#-理想,并且L#(a)也是左#-理想,于是,L#(xa)⊆L#(a).

特别地,对于半群S的正则元素来说,上述所定义的偏序刚好就是文[12]所研究的正则元素偏序的情形.

类似地,可以证明≤r也是偏序.另外,直接验证可知,当≤l和≤r限定在E(S)时刚好就是ω.

现在,定义#-富足半群上的自然偏序为≤=≤l∩≤r.容易看出,我们所定义的偏序正是正则或富足半群上的自然偏序的的一个推广[12-13].

3 主要结果

引理3[7]设S是H#-富足半群,则H#是同余当且仅当对任意的a,b∈S,(ab)0=(a0b0)0.

引理4[7]密码H#-富足半群S是完全J#-单半群Sα的半格Y,记为S=(Y,Sα).

命题2设S=(Y,Sα)是一个密码H#-富足半群.则下列命题成立:

(1)若a∈Sα且α≥β,则存在b∈Sβ使得b≤a;

(2)若a,b,c∈S,bH#c且b,c≤a,则b=c;

(3)若a∈E(S),b∈S且有b≤a,则b∈E(S).

证明(1)令a∈Sα,b1∈Sβ.因为H#是同余,且注意到aH#a0,有

(2)若a,b,c∈S,b,c≤a,则存在e,f,g,h∈E(S)使得b=ea=af,c=ga=ah.因为S是H#-富足半群,且注意到eb=b,bH#b0,从而有eb0=b0.类似地有c0h=c0.又bH#c,所以ec=ec0c=eb0c=b0c=c0c=c.类似可得bh=b.于是b=bh=eah=ec=c.

(3)若a,b∈S且b≤a,则存在e,f∈E(S)使得b=ea=af.又因为a∈E(S),所以

这即表明b∈E(S).

命题3设S=(Y,Sα)是正规密码H#-富足半群,则下列命题成立:

(1)若a∈Sα,则对任意的α≥β,存在唯一的aβ∈Sβ使得aβ≤a;

(2)对于任意的α≥β,若对于a∈Sα,b∈Sβ,存在幂等元e∈Sα使得e≤a0,则有eab= ab,bae=ba,ea=ae以及(ea)0=e.

证明(1)由命题2的(1)及其证明过程可知,对任意c∈Sβ,存在b=a(aca)0=(aca)0a∈Sβ使得b≤a.下证这样的b是唯一的.

现假定还存在b1∈Sβ,使得b1≤a,则此时存在g,h∈E(S),满足b=ga=ah.因为H#是同余,于是有

这即表明,bH#≤aH#,b1H#≤aH#.又因为,S/H#是正规带,它可分解为矩形带的(强)半格,故有S/H#=(Y,Sα/H#),从而

同理可得bae=ba.另外,因为该式是对任意的b∈Sβ都成立,所以可取b=e,此时,有ae=ea,由引理3,即可得(ea)0=(ea0)0=e.

命题4设S是密码完全J#-单半群,∀a,b∈S,若b≤a,则有b=a.

证明∀a,b∈S,若b≤a,则存在e,f∈E(S)使得b=ea=af.因为S是H#-富足半群,且注意到eb=b,bf=b,从而有ba0=b=a0b.又bH#b0,所以a0b0=b0=b0a0,即b0≤a0.又因为S是完全J#-单的,所以由引理4得a0=b0,即有aH#b.显然a,b≤a,故由命题2(2)可得b=a.

命题5若ϕ是密码完全J#-单半群S到密码完全J#-单半群T的同态,则对于任意的a∈S有(aϕ)0=a0ϕ.

证明首先,因为a0ϕ=(a0a0)ϕ=(a0ϕ)(a0ϕ)=(a0ϕ)2,所以a0ϕ∈E(T).另外

这即表明:(aϕ)0≤(a0ϕ).又T是完全J#-单半群,由引理4可得(aϕ)0=(a0ϕ).

从上面命题的证明过程可知,密码完全J#-单半群之间的同态ϕ其实是保持格林关系H#,L#, R#的,当然格林关系D#也将被保持.

定理1H#-富足半群S是正规密码H#-富足半群当且仅当它是完全J#-单半群的强半格.

证明(⇐)设半群S是S=(Y,Sα,ϕα,β)是完全J#-单半群Sα的强半格Y,下面证明S是正规密码H#-富足半群.为此,只需证明H#是S上的同余及S/H#是个正规带.

i)先证H#是S上的同余.对于任意的a∈Sα,b∈Sβ,有ab=aϕα,αβbϕβ,αβ.注意到密码完全J#-单半群间的同态保持相应的格林关系,再由命题5,有

于是,由引理3,H#是同余.

ii)再证S/H#是个正规带.首先,由于H#是同余,则S/H#是个带,并且此时Sα/H#是矩形带.设a∈Sα,b∈Sβ,c∈Sγ,并令δ=αβγ.于是

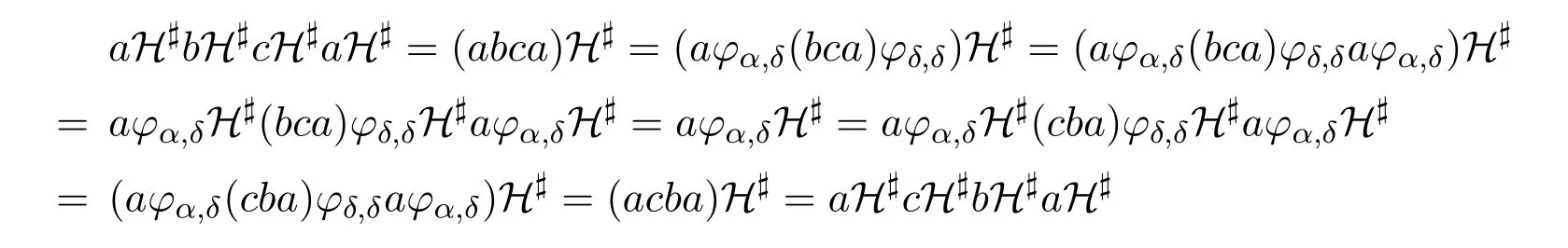
这即表明S/H#是个正规带.

(⇒)设半群S是正规密码H#-富足半群,由引理4,有S=(Y,Sα),其中Y为半格,并且对于任意的α∈Y,Sα为完全J#-单半群.对于α≥β及任意的a∈Sα,定义映射ϕα,β:Sα→Sβ,a 7→aβ,其中aβ是在命题3中使得aβ≤a成立的Sβ中的唯一的元素,并且对任意的c∈Sβ,有

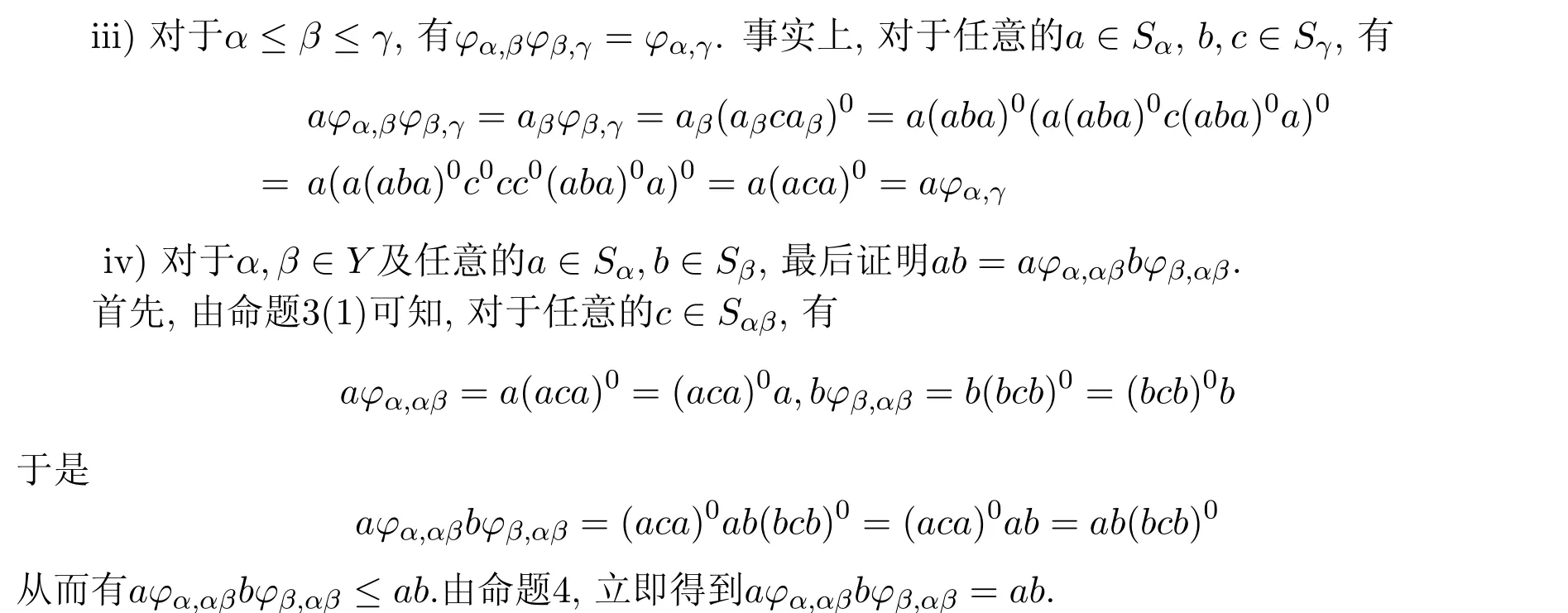
综上,证明了S=(Y,Sα,ϕα,β)是完全J#-单半群Sα的强半格.

注意到H#-富足半群是超富足半群的推广,于是在定理1中,如果把H#-富足半群限定在超富足半群上讨论,则此时正规密码H#-富足半群刚好就是正规密码超富足半群,完全J#-单半群正好就是完全J∗-单半群.于是,得到文[8]中的定理4.3,即为下面的推论:

推论1超富足半群S是正规密码超富足半群当且仅当它是完全J∗-单半群的强半格.

此外,在定理1中,如果我们把H#-富足半群再限定在完全正则半群上考虑,则此时正规密码H#-富足半群刚好就是正规密码群并半群,完全J#-单半群也正好就是完全单半群.同样地,可以得到如下推论

推论2完全正则半群S是正规密码群并半群当且仅当它是完全单半群的强半格.

[1]Mcalister D B.One-to-one partial right translations of a right cancellative semigroup[J].J.Algebra,1976,43:231-251.

[2]Pastijn F.A representation of a semigroup by a semigroup of matrices over a group with zero[J].Semigroup Forum,1975,10:238-249.

[3]Fountain J B.Abundant semigroups[J].Proc.London Math.Soc.,1982,44(3):103-129.

[4]Ren X M,Shum K P.The structure of superabundant semigroups[J].Science in China,Ser.A,Math., 2004,47(5):756-771.

[5]Petrich M.The structure of completely regular semigroups[J].Trans.Amer.Math.Soc.,1974,189:211-236.

[6]Clifford A H,Petrich M.Some classes of completely regular semigroups[J].J.Algebra,1977,46:462-480.

[7]丁月,孔祥智.H#-富足半群[J].山东大学学报:理学版,2008,43(4):55-61.

[8]Kong X Z,Shum K P.On the structure of regular crypto semigroups[J].Comm.Algebra,2001,29(6):2461-2479.

[9]Howie J M.An Introduction to Semigroup Theory[M].London:Academic Press,1976.

[10]Howie J M.Fundamentals of Semigroup Theory[M].Oxford:Clarendon Press,1995.

[11]潘秀娟,邵勇,田俊华.乘法半群为正规纯整群的半环[J].纯粹数学与应用数学,2005,21(1):76-79.

[12]Nambooripad K S S.The natural partial order on a regular semigroup[J].Proc.Edinburgh Math.Soc., 1980,23:249-260.

[13]Lawson M V.The natural partial order on an abundant semigroup[J].Proc.Edinburgh Math.Soc., 1987,30:169-186.

A construction of normal crypto H#-abundant semigroups

CHEN Yi-zhi1,2,SHAO Yong2

(1.Department of Mathematics,Huizhou University,Huizhou516007,China; 2.Department of Mathematics,Northwest University,Xi’an710127,China)

In this paper,a new construction theorem of normal crypto H#-abundant semigroups is given,i.e., an H#-abundant semigroup is a normal crypto H#-abundant semigroup if and only if it is a strong semilattice of completely J#-simple semigroups.Actually,the main result in this paper is a generalization of the corresponding ones of normal crypto semigroups and normal cryptogroups in superabundant and completely regular semigroups respectively.

Green’s#-relations,normal crypto H#-abundant semigroups,completely J#-simple semigroups, strong semilattice

O152.7

A

1008-5513(2009)04-0794-07

2008-11-10.

广东省自然科学基金(8151601501000002,9151051501000066),广东惠州学院校立基金(C208·0403,A08002).

陈益智(1980-),博士,讲师,研究方向：代数学.

2000MSC:20M10