Thermodynamic Properties for Polybrominated Dibenzothiophenes by Density Functional Theory*

LI Jiayou (李加友), LIU Hongxia (柳红霞), YU Hongxia (于红霞), WANG Zunyao (王遵尧),** and WANG Liansheng (王连生)



Thermodynamic Properties for Polybrominated Dibenzothiophenes by Density Functional Theory*

LI Jiayou (李加友)1, LIU Hongxia (柳红霞)1, YU Hongxia (于红霞)2, WANG Zunyao (王遵尧)1,**and WANG Liansheng (王连生)2

1School of Biological and Chemical Engineering, Jiaxing University, Jiaxing 314001, China2Department of Environment, Nanjing University, Nanjing 214007, China

The thermodynamic properties of 135 polybrominated dibenzothiophenes (PBDTs) inthe gaseous state at 298.15 K and 1.013×105Pa, are calculated using the density functional theory (the B3LYP/6-311G**) with Gaussian 03. Based on these data, the isodesmic reactions are designed to calculate the standard enthalpy of formation (Δfө) and the standard Gibbs energy of formation (Δfө) of PBDTs. The relations of these thermodynamic parameters with the number and position of bromine substituents (PBS) are discussed, and it is found that there exist good correlations between thermodynamic parameters (including heat capacity at constant volume, entropy, enthalpy, free energy, Δfө, Δfө) andPBS. The relative stability order of PBDT congeners is proposed theoretically based on the relative magnitude of their Δfө. In addition, the values of molar heat capacities at constant pressure (C,m) for PBDT congeners are calculated.

polybrominated dibenzothiophenes, density functional theory, method of position of substituted Br atom, thermodynamic parameters, relative stability

1 Introduction

Dibenzothiophene (DBT) (the structure and atomic numbering of DBT are illustrated in Fig. 1) and its derivatives are a group of important organic synthetic intermediates and are widely used in the synthesis of pesticide, medicine, biology and dyestuff [1]. Polybrominated dibenzothiophenes (PBDTs) are significant derivatives of DBT. In terms of the numbers and different positions of constituted bromine atoms, there are 135 possible PBDT compounds. It is important to know the structural and thermodynamic properties of PBDTs for studying their generation, degradation and potential environmental risk. Generally, thermodynamic parameters are obtained by precise experimental measurements. But for the difficulty of experimental measurements, many theory methods have been developed to predict these parameters. For example, Reed. [2] used three procedures for estimating thermodynamic stability and charge distribution for unknown molecules such as nitro derivatives of cubane, and the results suggest that hexa- and octa-nitrocubane are thermodynamically stable species. Taskinen. [3] measured theandforms of 1-propenylbenzene over the temperature range of 50-170°C by chemical equilibration in dimethyl sulfoxide (DMSO) solution with-BuOK as catalyst. The values of the thermodynamic parameters Δө, Δөand Δөat 298.15 K for each isomerization reaction between the title compounds were evaluated and the relative thermodynamic stabilities of the isomeric propenylbenzenes were studied. Xiao. [4] calculated the enthalpy of formation for 21 polynitrocubane compounds using semiempirical molecule orbit (MO) methods (MINDO/3, MNDO, AM1 and PM3) and for eight of 21 polynitrocubanes containing one to four nitro groups using the density functional theory at the B3LYP/6-31G* level by means of designed isodesmic reactions, and the results showed that the isodesmic reactions are more accurate and reliable. Furthermore, they also studied the thermodynamic functions for phenanthrene and anthracene using density functional theory (DFT) and ab initio methods, of which the thermodynamic functions calculated were in good agreement with the experimental results [5]. Yu. [6] and Feng. [7] researched the standard enthalpies of formation of alkyl derivatives with a novel topological indexxand molecular connectivity index of atomic ordinal number, respectively, and the results are satisfactory. Cao. [8] estimated the enthalpies of formation for mono-substituted alkanes in the liquid- phase based on the electrostatic effects of the alkyl R and the substituent, of which each of the items in the equation has its explicit physical meaning and the obtained equation can be favorable of further understanding of the correlation between molecular structures and their properties. Qiu. [9] studied quantitative- structure property relationship between intrinsic vibrational frequencies and thermodynamic properties of alkanes, and the predicted values were in good agreement with the experimental results. The results from referrences indicated that theoretical calculation is an important means for predicting thermodynamic functions, especially for the toxicit compounds and those obtained difficultly. Molecular simulations is broad applied in chemical engineering. In particular, when the parameters cannot be determined by experiment, they can be obtained by molecular simulation [10,11]. In our previous reports, the thermodynamic data of polychlorinated dibenzo--dioxins (PCDDs), polychlorodibenzofurans (PCDFs), polychlorinated biphenyls (PCBs) and polychlorinated naphthalenes (PCNs) have been calculated by DFT [12-15]. It was found that the isomers with low Gibbs energy have high formation ratio,.., the formation ratio of isomers are consistent with their relative stabilities. Moreover, Li. [16] calculated heat capacities, standard enthalpies of formation and entropies for 339 polybrominated/chlorinated dibenzo--dioxins (PXDDs) in the gaseous state using DFT and analysed the relationship between thermodynamic properties and the substitute number of bromine and chlorine. In addition, B3LYP density functional theory calculations have been carriedout on a number of PCDFs using 6-31G* and 6-311G**basis sets to estimate their enthalpies of formation based on the known experimental values of dibenzofuran, benzene and chlorobenzene [17]. Zeng. [18] calculated the thermodynamic properties of 39 polybrominated diphenyl ethers (PBDEs) in the ideal gas phase at the B3LYP/6-31G* level in Gaussian 03 program. Also, thermodynamic data of polybrominated dibenzo-furans (PBDFs) and polybrominated naphthalenes (PBNs) were calculated by the same method [19, 20], and the relative stabilities of their isomers were theoretically proposed. As is known, however, the thermodynamic data of PBDTs have not been reported.

Figure 1 Numbering of carbon atoms in DBT

In the present study, DBT and 135 PBDTs are fully optimized at the B3LYP/6-311G** level. The correlations of thermodynamic properties with the number and position of Br substitution (PBS) are discussed. Finally, by designing isodesmic reactions, the standard enthalpies of formation (Δfө) and the standard Gibbs energies of formation (Δfө) of 135 PBDTs are obtained. The stability order of the isomers are discussed based on the magnitude of the relative standard Gibbs energy of formation.

2 Computational method

All calculations are carried out with Gaussian 03 program [21]. The geometries of all PBDTs are optimized at the B3LYP/6-311G** level and frequency calculations are performed to ensure they are minimal at potential energy surface.

Thermodynamic parameters, such as standard enthalpies (ө), standard Gibbs energies (ө), standard entropy (ө), standard heat capacities at constant volume (ө), are obtained from computation.

In this work, PBDT isomers with one to eight bromine atoms are represented by the notation MBDT, DBDT, tri-DBT, TBDT, penta-BDT, hexa-BDT, hepta-BDT and OBDT, respectively. In addition, the positions of Br substitution (PBS) are consisted of the number of substituting Br atoms on the different positions of the parent compound and the number of relative positions of these Br atoms. The numbers of bromine atoms at position 1 or 9 are defined as1, at position 2 or 8 as2, at position 3 or 7 as3, at position 4 or 6 as4. The pair numbers of ortho, meta and para positions of bromine atoms on one benzene ring are symbolized aso,mandp. The numbers of bromine atom at positions 1 and 9 synchronously are1,9. Moreover, the parameters mentioned above are defined as a general designationPBS.

2.1 Comparison of different calculation methods

Generally, the computational precision increases as the basis set size increases, but in view of the calculation power of computers, four MBDTs with three levels (B3LYP/6-311G**, B3LYP/6-311++G**, MP2/6-31G*) are calculated. Based on computation results of the present study, the values of thermodynamic parameters with B3LYP/6-311++G** and MP2/6-31G* methods are similar to those from B3LYP/6-311G** for MBDTs, and the differences between them are less than 3% (the values are listed in Table 1). Among these parameters, the values ofө,өand total energy (TE) with B3LYP/6-311G** method are close to those with B3LYP/6-311++G** method. As for MP2/6-31G* method, because the basis set is too large, the frequency does not calculated. Thus, only total energy values at MP2/6-31G* level are obtained. Furthermore, the total energy values and their orders from three methods are consistent. Based on comparative analysis, the B3LYP/6-311G** level is acceptable. In addition, calculation at B3LYP/6-311++G** and MP2/6-31G* levels would spend more computer time, thus, B3LYP/6-311G** calculation for all 135 PBDTs is chosen in the present study.

Furthermore, some of PBDT congeners are calculated using diffuse functions (B3LYP/6-311++G**) and obtained their Δfөand Δfө. Then the results are compared with those from B3LYP/6-311G**, and all values are listed in Table 2. Table 2 shows that the differences are no more than 38.0 kJ·mol－1. These differences are not dramatic compared to an average absolute deviation of 44.35 kJ·mol－1for Rabuck’s test set [22]. The diffuse basis sets allow orbitals to occupy a larger region of space. They usually make an improvement in accuracy of energies. Absence of diffuse basis sets increases the mean absolute deviations of energies by 16.74 kJ·mol－1over the G2 test set [23]. However, computations of all data with diffuse functions for the title compounds will be too expensive in computing source. Thus, all PBDT congeners using diffuse functions are not calculated.

Table 1 The total energy values from different levels

2.2 Isodesmic reactions

By designing isodesmic reactions, as reaction 1, Δfөand Δfөof PBDTs are obtained.

The standard enthalpy change of the reaction (Δrө) is equal to the sum of the standard enthalpies of the products obtained from DFT calculations minus the sum of the standard enthalpies of reactants:

where PhH and BB represent benzene and bromobenzene, respectively.

The sum of the standard enthalpies of formation of the products minus those of the reactants yields Δrө:

By substituting Eq. (3) into Eq. (2), ΔfөPBDTcan be obtained by Eq. (4):

∆fөPBDTsөPBDTsөPhHөBBөDBT

∆fөPhH∆fөBB∆fөDBT(4)

Similarly, ΔfөPBDTis obtained by Eq. (5):

∆fөPBDTsөPBDTsөPhHөBBөDBT

∆fөPhH∆fөBB∆fөDBT(5)

The experimental values of Δfөand Δfөfor dibenzothiophene, bromobenzene and benzene are taken from references [24, 25] and the values ofөandөfor these compounds are calculated at the B3LYP/6-311G** level. Since all the values of the thermodynamic parameters mentioned above are from theoretical calculations, variables can be exactly repeatable.

3 Results and discussion

All the thermodynamic properties withPBSof PBDTs, calculated at the B3LYP/6-311G** level, are listed in Table 4.

3.1 Relations of thermodynamic properties and NPBS

The multiple linear regression method of the SPSS 12.0 for Windows is used to obtain the correlations ofө,ө,өandөwithPBSfor PBDTs, and the results are as following Eqs. (6) and (7):

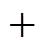
4.24(±0.03)4(6)

Table 2 The values of ΔfHө and ΔfGө from diffuse functions and the differences for some PBDTs

Table 3 The difference between the calculated thermodynamic parameters by B3LYP/6-311G** and experimental ones

① Taken from Ref. [27].

Table 4 The thermodynamic data of PBDTs from DFT calculations at B3LYP/6-311G** level

MoleculeCөv /J·mol－1·K－1Sө/J·mol－1·K－1ΔfHө/kJ·mol－1ΔfGө/kJ·mol－1ΔfGөR/kJ·mol－1Cp,mA+B×10－3T+C×103T－1+D×107T－2N1N2N3N4NoNmNpN1,9 A/J·mol－1·K－1B/J·mol－1·K－2C/J·mol－1D/J·mol－1·K tri-BDT 1,2,9214.6512.5275.5332.586.4555.3191.22021001001 1,3,4214.6517.1218.0273.727.5554.4181.23010111110 1,3,6215.1518.8202.9258.112.0553.9171.22310110100 1,3,7215.1520.1200.4255.19.0553.6341.21810200100 1,3,8215.1520.1201.6256.410.3553.7541.21811100100 1,3,9215.1515.1258.8315.068.9554.9101.21820100101 1,4,6214.6517.6205.2260.714.6554.1061.22610020010 1,4,7215.1518.8202.2257.411.2553.8391.22110110010 1,4,8214.6518.8203.5258.812.6553.9441.22211010010 1,4,9214.6514.2261.2317.871.7555.1221.22320010011 1,6,7214.6516.7213.4269.123.0554.1791.22510111000 1,6,8214.6518.4203.4258.612.5554.0581.22411010100 1,7,8215.1518.4213.3268.622.5553.9551.22011101000 2,3,4214.6516.3220.6276.630.5554.3971.23001112100 2,3,6214.6518.0203.8259.213.1553.7941.22301111000 2,3,7215.1519.2202.0257.010.9553.4581.21701201000 2,3,8215.5519.7202.5257.511.4553.4861.21702101000 2,4,6215.1518.8193.3248.42.3553.8361.22601020100 2,4,7215.1520.1191.3246.10.0553.5841.22001110100 2,4,8215.1520.1192.1246.90.8553.6201.22202010100 2,6,7214.6518.0202.4257.911.8553.7921.22301111000 3,4,6214.6517.1204.2259.913.8554.0141.22700121000 3,4,7215.1518.0202.2257.611.4553.7431.22200211000 TBDT 1,2,3,4232.6556.1284.3327.662.5561.8781.15411113210 1,2,3,6232.6558.6264.7307.342.3561.1291.14611112100 1,2,3,7233.0559.4261.9304.239.1560.8371.14211202100 1,2,3,8233.0559.4263.2305.640.5560.9351.14212102100 1,2,3,9232.6552.7320.1364.599.4562.1161.14421102101 1,2,4,6232.6559.0251.6294.129.0560.9791.14911021110 1,2,4,7233.0559.8248.9291.226.1560.7421.14511111110 1,2,4,8233.0559.8250.1292.327.2560.7711.14512011110 1,2,4,9232.6553.1307.5351.886.7562.0511.14821011111 1,2,6,7232.6558.1258.0300.835.7560.8821.14511112000 1,2,6,8232.6559.4248.3290.725.6560.7981.14412011100 1,2,6,9232.6553.1305.8350.185.1561.8671.14421011011 1,2,7,8233.0559.4257.9300.335.2560.6411.14012102000 1,2,7,9233.0554.8303.5347.382.2561.6491.14021101101 1,2,8,9232.6551.9320.0364.699.5562.0301.14222002001 1,3,4,6232.6558.1246.5289.324.2560.7671.15010121110 1,3,4,7232.6559.0243.7286.121.1560.5351.14510211110 1,3,4,8233.0559.4244.9287.322.2560.6061.14611111110

MoleculeCөv /J·mol－1·K－1Sө/J·mol－1·K－1ΔfHө/kJ·mol－1ΔfGө/kJ·mol－1ΔfGөR/kJ·mol－1Cp,mA+B×10－3T+C×103T－1+D×107T－2N1N2N3N4NoNmNpN1,9 A/J·mol－1·K－1B/J·mol－1·K－2C/J·mol－1D/J·mol－1·K TBDT 1,3,4,9232.6554.0301.8345.980.8561.8311.14820111111 1,3,6,7232.6559.4242.1284.519.4560.4881.14410211100 1,3,6,8233.0561.5232.4274.29.1560.3421.14311110200 1,3,6,9233.0556.1289.2332.667.5561.4611.14220110111 1,3,7,8233.0560.7242.2284.219.1560.2721.13911201100 1,3,7,9233.0557.3287.0330.064.9561.1791.13820200201 1,4,6,7232.6558.1244.0286.821.7560.6371.14710121010 1,4,6,8232.6559.8234.4276.711.6560.5351.14711020110 1,4,6,9232.6555.6292.1335.770.6561.6061.14620020021 1,4,7,8232.6559.4243.9286.221.2560.4551.14311111010 2,3,4,9232.6557.3258.4301.536.4561.0181.14911112100 2,3,4,6232.6557.3249.2292.327.2560.8551.15101122100 2,3,4,7233.0559.0247.1289.724.6560.5151.14501212100 2,3,4,8233.0558.6247.8290.425.4560.5611.14602112100 2,3,6,7232.6559.0243.8286.321.2560.3251.14401212000 2,3,6,8233.0560.7233.4275.410.4560.1671.14302111100 2,3,7,8233.0559.4243.7286.121.0560.1121.14002202000 2,4,6,7233.0559.8233.3275.510.5560.3421.14601121100 2,4,6,8233.0561.1223.2265.10.0560.2481.14602020200 3,4,6,7233.0559.8233.3275.510.5560.3421.14600222000 penta-BDT 1,2,3,4,6250.2597.5313.0343.337.5568.3421.07511123210 1,2,3,4,7250.6598.3310.0340.034.2568.0521.07011213210 1,2,3,4,8250.6598.3311.4341.535.7568.1651.07112113210 1,2,3,4,9250.6591.2367.4399.693.8569.3481.07421113211 1,2,3,6,7250.6598.3304.0334.128.3567.7061.06811213100 1,2,3,6,8250.6600.0294.4323.918.1567.6131.06712112200 1,2,3,6,9250.6593.7350.9382.476.6568.6711.06721112111 1,2,3,7,8250.6599.1303.8333.627.8567.5421.06412203100 1,2,3,7,9251.0594.5348.6379.874.0568.4821.06321202201 1,2,3,8,9250.6592.5365.0396.991.1568.8641.06522103101 1,2,4,6,7250.2598.7290.9321.015.1567.5361.07111122110 1,2,4,6,8250.6600.8281.6310.95.0567.4751.07012021210 1,2,4,6,9250.6595.0338.7369.864.0568.5551.07121021121 1,2,4,7,8250.6600.4290.7320.214.4567.3491.06712112110 1,2,4,7,9250.6595.4336.1367.161.3568.4271.06821111211 1,2,4,8,9250.6592.9352.5384.278.4568.7951.06922012111 1,2,6,7,8250.6597.9303.4333.527.7567.7581.06912113100 1,2,6,7,9250.6593.7346.7378.272.4568.5841.06921112111 1,3,4,6,7250.2598.3285.7315.810.0567.3471.07210222110 1,3,4,6,8250.6600.0276.3305.80.0567.3471.07211121210 1,3,4,6,9250.6595.0332.9364.058.1568.3601.07120121121

MoleculeCөv /J·mol－1·K－1Sө/J·mol－1·K－1ΔfHө/kJ·mol－1ΔfGө/kJ·mol－1ΔfGөR/kJ·mol－1Cp,mA+B×10－3T+C×103T－1+D×107T－2N1N2N3N4NoNmNpN1,9 A/J·mol－1·K－1B/J·mol－1·K－2C/J·mol－1D/J·mol－1·K penta-BDT 1,3,4,7,8250.6600.0285.7315.49.5567.1771.06711212110 1,3,4,7,9250.6595.8330.4361.255.3568.2041.06720211211 1,3,6,7,8250.6599.1287.7317.511.7567.3631.06811212200 1,4,6,7,8250.6598.3289.6319.613.8567.4951.07111122110 2,3,4,6,7250.6597.5289.0319.313.5567.3181.07101223100 2,3,4,6,8250.6599.6279.1308.83.0567.2361.07102122200 2,3,4,7,8250.6598.7289.1319.113.3567.0971.06702213100 hexa-BDT 1,2,3,4,6,7268.2637.6352.3369.921.1574.9120.99611224210 1,2,3,4,6,8268.6639.3343.2360.311.5574.8350.99512123310 1,2,3,4,6,9268.2631.8398.6418.069.2575.9230.99821123221 1,2,3,4,7,8268.6638.9352.2369.520.6574.7400.99212214210 1,2,3,4,7,9268.6633.5396.2415.166.3575.7140.99421213311 1,2,3,4,8,9268.2630.5412.4432.283.4576.1370.99622114211 1,2,3,6,7,8268.6638.5349.6367.018.2574.5660.99112214200 1,2,3,6,7,9260.7615.0420.3444.795.8575.4170.99221213211 1,2,3,6,8,9261.1617.6451.8475.5126.6576.2790.97822113211 1,2,3,7,8,9268.6639.3336.9354.15.3574.4440.99522204201 1,2,4,6,7,8268.2634.3379.9398.549.7575.3390.99612123210 1,2,4,6,7,9268.2633.9385.8404.555.7575.5680.99721122221 1,2,4,6,8,9268.6632.6397.8417.068.1575.6330.99322022221 1,3,4,6,7,8268.6638.5331.4348.80.0574.2560.99511223210 1,3,4,6,7,9268.2634.3379.9398.549.7575.3310.99620222221 2,3,4,6,7,8268.2637.6335.1352.73.9574.2040.99602224200 hepta-BDT 1,2,3,4,6,7,8286.2677.4398.2403.30.0581.8340.92112225310 1,2,3,4,6,7,9286.2672.0439.8446.543.2582.6550.92221224321 1,2,3,4,6,8,9286.2672.0445.6452.449.1582.8510.92322124321 1,2,3,4,7,8,9286.2670.7457.8464.961.6582.9500.91922215311 OBDT 1,2,3,4,6,7,8,9303.8709.6505.8500.6590.1690.84922226421

Note:өis standard entropy,өis standard heat capacity at constant volume, Δfөis the standard enthalpy of formation of the compound, Δfөis the standard Gibbs energy of formation of the compound and ΔfөRis the relative magnitude of the standard Gibbs energy of formation.is the number of Br atom substitutions and that subscript PBS indicates the positions.

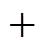
Equations (6) and (7) show that there exist good correlations between the values obtained from Gaussian 03 program andPBS, and these parameters can be predicted with reasonable accuracy from thePBSof PBDTs,.., theөandөvalues of PBDTs obviously vary with the substitute number and position of bromine atoms. This is consistent with that of the study on substituted chlorine of PCDFs, PCNs and PCDDs [12, 14, 26].

3.2 Calculated results of ΔfHө and ΔfGө and relative stability of isomer groups

With the design of isodesmic reactions, Δfөand Δfөof PBDTs are obtained. On the basis of the lowest Δfөof isomers with the same substitute numbers of bromine atoms, the obtained relative standard Gibbs energies of formation are listed in Table 4. It can be found that the values of Δfөand Δfөincrease with increasing number of bromine atoms (except monosubstituted),.. stability decreases with increasing bromination. For example, among 28 isomers of penta-BDTs, 1,3,4,6,8-penta-BDT possesses the lowest value of Δfө, and 1,2,3,4,9-penta-BDT possesses the highest corresponding value, where the discrepancy of them is 94 kJ·mol－1. In the same way, the Δfөof 1,3,4,6,7,8-hexa-BDT is lower than those of the other 15 isomers, and 1,2,3,6,8,9-hexa-BDT is higher than those of the other 15 isomers, where the discrepancy of them is 127 kJ·mol－1.

The most stable and unstable isomers as indicated by the Gibbs energy of formation are listed in Table 5. These results can be used to examine whether the most stable isomers are the most abundant in the environment. It can be seen from Table 5, the most unstable isomers in MBDTs, DBDTs, tri-BDTs, TBDTs, penta-BDTs, hexa-BDTs and hepta-BDTs are all those with bromine being attached to 1, 9 positions simultaneously. On the contrary, the most stable isomers are all those with bromine being attached to 4, 6 positions simultaneously. The reason is that the bromine substituent at positions 1 and 9 synchronously seems to destabilize the isomers, and the resulting steric effect may be one of the important sources of the relative instabilities of the PBDTs apart from the associated electrostatic effects. For instance, the distances between bromines atoms substituent at positions 1 and 9 is 0.3304 nm, which is smaller than that of bromines atoms substituent at positions 4 and 6 (0.6356 nm), where the steric effect of the former is obviously larger than that of the latter.

Using SPSS 12.0 for Windows, the correlation expressions of Δfөand ΔfөtoPBSfor PBDTs are summarized and presented in Eqs. (8) and (9).

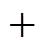
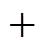
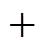
(46.6±3.4)1,9(8)

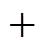
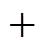
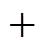
(48.4±3.5)1,9(9)

Equations (8) and (9) clearly demonstrate that the substitute number and positions of bromine atoms influence the values of Δfөand Δfө. The values of Δfөincrease with increasing substitute number of bromine atoms, and the effect of1,9is important. When1,9is changed from 0 to 1, the value of Δfөincreases 46.6 kJ·mol－1. But the effect ofo,mandpon Δfөis relatively small. Thus,1,2,3,4and1,9are the primary factors influencing the values of Δfө. The values of Δfөalso increase with the number of bromine atoms, and1,9is the primary influence on the values of Δfө. When1,9is changed from 0 to 1, the value of Δfөincreases 48.4 kJ·mol－1.o,mandphave a great effect on the values of Δfө, and the order iso>p>m.

3.3 The temperature dependence of molar heat capacity at constant pressure for PBDTs

Table 5 The most stable and the most unstable isomers indifferent isomer groups for PBDTs

Table 6 The difference between calculated and experimental value of Cp,m

① Taken from Ref. [24];②Calculated using statistical thermodynamics calculation program.

Using the calculated values ofC,mof PBDTs at different temperature (), the relations betweenC,mand temperature are obtained by the least square method and are listed in Table 4.is a constant,,andare regression coefficients. Table 4 shows that almost all PBDT congeners have very good relationships betweenC,mand temperature (,－1and－2), and the correlation coefficients (2) are all equal to 1.0 and all the standard deviations (SD) are low. These indicate that the correlation betweenC,mvalues andis good.

4 ConclusionS

Fully optimized calculation of 135 PBDTs are carried out at the B3LYP/6-311G** level with Gaussian 03 program, and their thermodynamic parameters are obtained. By designing isodesmic reactions, the standard enthalpies of formation (Δfө) and the standard Gibbs energies of formation (Δfө) are also calculated. The correlations between thermodynamic parameters andPBSare discussed. It is found that there exist good correlations between thermodynamic parameters andPBS. These parameters include heat capacity at constant volume (ө), entropy (ө), standard enthalpy of formation (Δfө) and standard free energy of formation (Δfө). The stability order of the isomers is discussed based on the magnitude of the relative standard Gibbs energy of formation. The correlations have some significances for synthesizing these isomers. Furthermore, on the basis of the relative stability, the reaction activities of these isomers are known. Thus, this work is significant because the relative stability of isomers and their toxicities are synchronously considered in circumstance toxicological research.

NOMENCLATURE

C,mmolar heat capacity at constant pressure , J·mol－1·K－1

өheat capacity at constant volume, J·mol－1·K－1

Δfөstandard free energy of formation, kJ·mol－1

ΔfөRrelative magnitude of the standard Gibbs energy of formation, kJ·mol－1

Δfөstandard enthalpy of formation, kJ·mol－1

number of substituting Br atoms on the different positions of parent compound and the number of relative positions for these Br atoms

1numbers of bromine atoms at positions 1 or 9

1,9numbers of bromine atom at positions 1 and 9 synchronously

2numbers of bromine atoms at positions 2 or 8

3numbers of bromine atoms at positions 3 or 7

4numbers of bromine atoms at positions 4 or 6

mpair numbers of meta positions of bromine atoms on one benzene ring

opair numbers of ortho positions of bromine atoms on one benzene ring

ppair numbers of para positions of bromine atoms on one benzene ring

2correlation coefficients

өentropy, J·mol－1·K－1

SD standard deviations

temperature, K

Superscript

ө standard state

Subscripts

f formation

m molar

PBS positions of Br substitution

R reaction

1 Li, J.Y., Zhou, X.R., Zhao, D.F., “Dibenzothiophene and derivatives”,, 68, 1-7 (2005).

2 Reed, L.H., Jayasuria, K., Koovakkat, S.K., Allen, L.C., “Estimation of thermodynamic stability and charge distribution for unknown molecules: Nitro derivatives of cubane”,...., 4, 714-720 (1991).

3 Taskinen, E., Lindholm, N., “Relative thermodynamic stabilities of the isomeric propenylbenzenes”,...., 7, 256-258 (1994).

4 Xiao, H.M., Gong, X.D., “Theoretical studies on heats of formation for polynitrocubanes using the density functional theory B3LYP method and semiempirical MO methods”,...., 14, 583-588 (2001).

5 Xiao, H.M., Gong, X.D., “Ab initio studies on the structures and thermodynamic functions of phenanthrene and anthracene”,...., 12, 441-446 (1999).

6 Yu, X.M., “A QSPR study on the standard enthalpy of formation of alkyl derivatives”,...., 20, 915-920 (2000).

7 Feng, C.J., Chen, Y., Li, M.J., “Research on the standard enthalpies of formation of alkyl derivatives based on molecular connectivity index of atomic ordinal number”,...., 22, 206-211 (2002).

8 Cao, C.Z., Gao, S., “A novel approach for estimating the enthalpies of formation of monosubstituted alkanes RX in liquid-phase”,..., 21, 1028-1035 (2005).

9 Qiu, M.H., Peng, B., Deng, L.Y., Gao, Y.Y., “Quantitative-structure property relationship between intrinsic frequencies with molecular structure vibrating and thermodynamic properties for alkannes”,...., 23, 127-131 (2006).

10 Fu, Y.F, Su, H.Y., Zhang, Y., Chu, J., “Adaptive soft-sensor modeling algorithm based on FCMISVM and its application in PX adsorption separation process”,...., 16 (5), 746-751 (2008).

11 Zhang, M.G., Zhang, L.H., Jiang, B., Yin, Y.G., Li, X.G., “Calculation of metzner constant for double helical ribbon impeller by computational fluid dynamic method”,...., 16 (5), 686-692 (2008).

12 Wang, Z.Y., Zhai, Z.C., Wang, L.S., “Prediction of gas phase thermodynamic properties of polychlorinated dibenzo-furans by DFT”,... (), 725, 55-62 (2005).

13 Wang, Z.Y., Wu, Y.C., Kikuchi, O., Watanabe, T., “DFT study of tetrachlorinated dibenzo--dioxins”,., 61, 840-845 (2003).

14 Wang, Z.Y., Han, X.Y., Zhai, Z.C., Wang, L.S., “Study on the thermodynamic property and relative stability of a series of polychlorinated biphenyls by density functional theory”,, 63, 964-972 (2005).

15 Zhai, Z.C., Wang, Z.Y., “Computational study on the relative stability and formation distribution of 76 polychlorinated naphthalene by density functional theory”,... (), 724 (1-3), 221-227 (2005).

16 Li, X.W., Shibata, E., Nakamura, T., “Thermodynamic properties of polybrominated/chlorinated dibenzo--dioxins calculated by density functional theory”,.., 44, 2441-2451 (2003).

17 Thompson, D., Ewan, B.C.R., “A group additivity algorithm for polychlorinated dibenzofurans derived from selected DFT analyses”,...., 111, 5043-5047 (2007).

18 Zeng, X., Freeman, P.K., Vasil’ev, Y.V., Voinov, V.G., Simonich, S.L., Barofsky, D.F., “Theoretical calculation of thermodynamic properties of polybrominated diphenyl ethers”,..., 50, 1548-1556 (2005).

19 Yu, J., Zhang, X.C., Wang, Z.Y., Zeng, X.L., “Study on the thermodynamic properties and stability of a series of polybrominated dibenzo-furans by density functional theory”,., 64, 1961-1968 (2006).

20 Yuan, L.X., Yu, J., Wang, Z.Y., Liu, H.X., Ju, X.H., “Thermodynamic property and relative stability of 76 polybrominated naphthalene by density functional theory”,..., 51, 2032-2037 (2006).

21 Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Zakrzewski, V.G., Montgomery, J.A., Stratmann, R.E., Burant, J.C., Dapprich, S., Millam, J.M., Daniels, A.D., Kudin, K.N., Strain, M.C., Farkas, O., Tomasi, J., Barone, V., Cossi, M., Cammi, R., Mennucci, B., Pomelli, C., Adamo, C., Clifford, S., Ochterski, J., Petersson, G.A., Ayala, P.Y., Cui, Q., Morokuma, K., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Cioslowski, J., Ortiz, J.V., Baboul, A.G., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Gomperts, R., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Andres, J.L., Gonzalez, C., Head-Gordon, M., Replogle, E.S., Pople, J.A., Gaussian 03 (Revision A.1), Gaussian, Inc., Pittsburgh, PA (2003).

22 Rabuck, A.D., Scuseria, G.E., “Assessment of recently developed density functionals for the calculation of enthalpies of formation in challenging cases”,..., 309, 450-456 (1999).

23 Foresman, J.B., Frisch, A.E., Exploring Chemistry with Electroinc Structure Methods, Gaussian, Inc., Pittsburgh, PA (1996).

24 Yao, Y.B., Xie, T., Gao, Y.M., Handbook of Physics and Chemistry, 1st edition, Shanghai Science and Technology Press, Shanghai (1985).(in Chinese)

25 Chirico, R.D., Knipmeyer, S.E., Nguyen, A., “The thermodynamic properties of dibenzothiophene”,.., 23, 431-450 (1991).

26 Wang, Z.Y., Zhai, Z.C., Wang, L.S., Chen, J.L., Kikuchi, O., Watanabe, T., “Prediction of gas phase thermodynamic function of polychlorinated dibenzo--dioxins using DFT”,... (), 672 (1-3), 97-104 (2004).

27 Dean, J.A., Lange’s Handbook of Chemistry, 13th edition, McGraw-Hill Book Company, New York (1985).

28 Raff, L.M., Principles of Physical Chemistry, Prentice Hall, New Jersey (2001).

2008-12-22,

2009-04-28.

the National Natural Science Foundation of China (20737001).

** To whom correspondence should be addressed. E-mail: wangzun315cn@163.com