Gas Flow in Unilateral Opening Pulse Tubes Based on Real Gas Equation of State

DAI Yuqiang (代玉强), HU Dapeng (胡大鹏), ZOU Jiupeng (邹久朋) and ZHAO Jiaquan (赵家权)



Gas Flow in Unilateral Opening Pulse Tubes Based on Real Gas Equation of State

DAI Yuqiang (代玉强)*, HU Dapeng (胡大鹏), ZOU Jiupeng (邹久朋) and ZHAO Jiaquan (赵家权)

School of Chemical Engineering, Dalian University of Technology, Dalian 116012, China

The real gas effect is dominant at high pressure and low temperature, and it is modeled by complex equations of state other than perfect gas law. In the vicinity of liquid-vapor critical point, the real gas exhibits unusual gas dynamic behavior. In the present work, a transient wave fields in unilateral opening pulse tube is simulated by solving the Navier-Stokes equations incorporated with the Peng-Robinson thermodynamic model. The computational fluid dynamics (CFD) results show a remarkable deviation between perfect gas model and real gas model for contact interface and shockwave. The wave diagram based on the real gas model can help to solve the problem of offset design point.

real gas flow, pulse tube, expansion refrigeration, unsteady flow

1 INTRODUCTION

Gas wave machine (GWM) has been widely used in natural gas processing industry in the last decade, but the designers are often perplexed with the off-design problems. The obstacles are mainly originated from unusual flow complexity and uncertainties about the selection of the best wave rotor configuration for a particular application. The main reason is that high molecular weight gas mixtures in pulse tubes of GWM at low temperature and high pressure may exhibit nonclassical phenomena in vapor region near the liquid-vapor critical point. They cannot get the precise port timing information from the GWM’s physical diagram or wave diagram under the assumption of idealgas model. Researchers refer to fluids that show nonclassicalflow properties as Bethe-Zel’dovich-Thompson (BZT) fluids [1]. In the nonclassical flow, the subsonic characteristic is extended to high Mach numbers [2, 3]; compression shockwaves disintegrate into a compression fan when entering the nonclassical region. Conversely, expansion waves may coalesce into expansion shockwaves. The main reason is the non-monotone variation of the Mach number with respect to density [4]. Thompson [5] first found that the sign of the fundamental derivative of gas dynamicsgoverns the nonlinear characters of gases:

The BZT fluid dynamics can be applied in many areas such as the organic Rankine cycle processes [6, 7] using organic substance like toluene as working fluid, Stirling engines, thermo-acoustic engines, supercritical fluids, refrigerants, and many types of multi-phase flows [8] for petrochemical processes and so on.

The application of computational fluid dynamics (CFD) to the above area is not widely spread. A main reason is the lack of a proper model for the fluid physical properties, since solvers are developed in most cases of the perfect gas behavior [9]. Fortunately, the computation of dense gas flows has received increasing attention in the last decade [4, 10-12], motivated by the mentioned engineering applications [13-15].

The main problem is how to couple the real gas state equation with the Navior-Stokes equations. We should choose a suitable method that is fast, accurate for CFD computations and flexible for the use with general state equations. The feasible approaches to this problem can be direct state equation representation and look-up table (LUT) algorithms [9]. The former method is the most straightforward one and, being analytical, has the advantage of the greatest numerical accuracy. It is actually an extension of the perfect gas model. The main drawback is the low computational efficiency. The later LUT method is based on the discretization of the actual state equation onto a structured mesh. This approach cuts down the computational effort in the solver. Some commercial CFD code like Fluent can use table look-up procedures obtained from the REFPROP developed by National Institute of Standards and Technology (NIST). Unfortunately, the REFPROP database does not supply a large number of pure fluids, especially those involved in deep refrigeration of natural gas industry. It follows that the creation of general LUT based specific PVT model like Peng-Robinson [16] thermodynamic model is necessary.

2 GOVERNING EQUATIONS AND THERMODYNAMIC MODELS OF REAL GASES

For using a general equation of state (EoS), the governing equations of motion for a general Newtonian fluid with an arbitrary equation of state and variable properties should be written in two-dimensional primitive form as

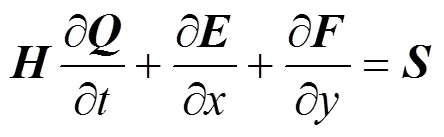
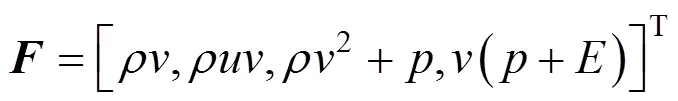
The diffusive matrixis related with viscosity of fluid [8]:

and

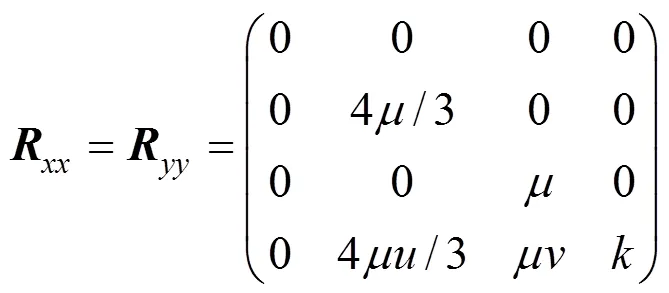
Total energyis related to the enthalpyby

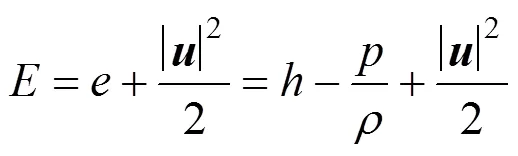
To realize the real flow analysis, an appropriate PVT relation and appropriate mixing rules should be chosen to calculate the key properties of the fluids like density, heat capacity, sound speed, viscosity and thermal conductivity. Peng-Robinson state equation is chosen for its high precision in prediction of vapor-liquid equilibria for systems containing non-polar components [16]:

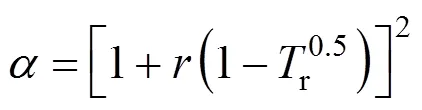
Figure 1 Sound speed (m·s－1) of C1/C2/C3mixtures (mass compositions: C179%-C28%-C313%) from the LUT based on Peng-Robinson EoS (solid) and Benedict-Webb-Rubin-Starling(BWRS) EoS [17] (dash)

3 REAL GAS FLOW IN PULSE TUBE

3.1 Numerical procedure

Pulse tubes are the main working parts in thermal separators, widely used in natural gas refrigeration industry. The movement behavior of contact interfaces between driving and driven gas and shockwaves formed in pulse tubes are of great importance for designing GWM and pressure exchanging refrigerators (PER). The model of a pulse tube is shown in Fig. 2: the unilateral opening tube is 200 mm long; the pressure in the pulse tube is 5.0 MPa with a sudden 15.0 MPa stream jetting at left. The fluids are chosen to be methane and methane/ethane/propane (C1/C2/C3) mixtures. A strong shockwave and a contact interface will form in the tube, and the shockwave will reflect at the right wall, then the reflective shockwave will meet with the contact interface.

Figure 2 CFD model of the pulse tube

Figure 3 Wave diagram of the pulse tube with pure methane gas (pressure ratio: 15 MPa/5 MPa, temperature: 300 K/300 K)

◇ real shockwave;□ real interface;△ ideal shockwave;○ ideal interface

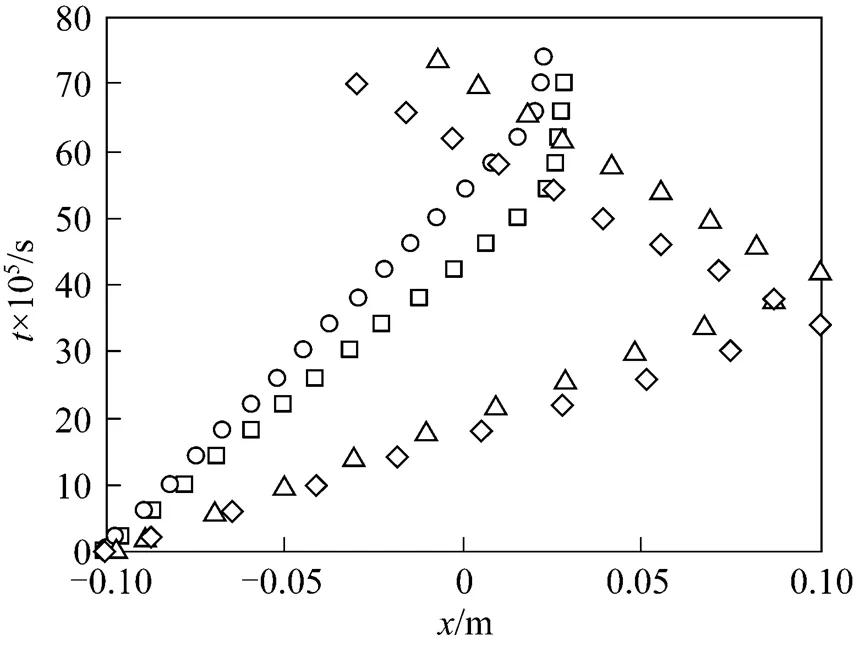
Figure 4 Wave diagram of the pulse tube with C1/C2/C3mixture: C179%-C28%-C313% (pressure ratio: 15 MPa/5 MPa, temperature: 300 K/300 K)

○ ideal interface;△ ideal shockwave;◇ real shockwave;□ real interface

The whole process of real flow in the tube will be shown in comparion with that based on perfect gas. A unified representation of mixtures is given by Amagat’s law [18] capable of handling arbitrary equations of state like Peng-Robinson thermodynamic equation.

3.2 Numerical results

Figure 3 shows the wave diagram of the pulse tube with pure methane gas. The contact interface and shockwave computed from ideal EoS are almost coincides with those from Peng-Robinson EoS. The real gas effect is not obvious for methane at 15 MPa and 300 K. The main reason is that methane has small molar weight and the state at given pressure and temperature is far from the dew point. It is shown that we can use perfect gas model when the flow takes place far from the dew point of fluid.

○ ideal; + real

But when the flow takes place in the vicinity of saturated vapor line or in the supercritical zone, the fundamental derivative of gas dynamicscan be smaller than unity [10], as governs the nonlinear dynamics of gases. Fig. 4 shows the wave diagram of the pulse tube with methane, ethane and propane mixtures. The mass compositions are 79%, 8% and 13% respectively. There are remarkable deviations between perfect gas model and real gas model for contact interface and shockwave. The slopes of incidence shockwave and the contact interface lines from real gas flow results are lower than those based on perfect gas. It is follows that there should be a larger velocity in real gas flows which can guide engineers to design the rotational thermal separators (RTS). By analyzing its real flow, the main the problem of offset design point is now resolved.

Figure 5 shows the temperature effect of the reflective shockwave meets with contact interface at 0.007 ms. The arrows show the propagating direction of shock and contact interface. For the real gas flow there is lower temperature rise. So if designing RTS using the ideal gas model, one will get a conservative design offset.

For refrigeration applications in natural gas industry, the unsteady characteristics of natural gas flow in the pulse tubes are also analyzed. The thermal separation properties and various wave velocities are invested. The natural gas components’ mass fractions are C1-87.5%, C2-5.62%, C3-2.13%,-C4--C4-0.034%,-C5--C5-0.016%,-C6and above 0.0, CO2-2.29% and N2-2.41%. The PVT relation is also from Peng-Robinson EoS and Fig. 6 shows the phase envelope curves. The CFD model is the same as before. To avoid supersaturation, the initial temperature in the tubes is set as 320 K. By plotting the contours of temperature and pressure values inandcoordinates, we can get the wave diagram (like Fig. 7) of the pulse tube from which the thermal separation properties and wave velocities is easily achieved. Tables 1 and 2 show the wave speeds and temperatures of each zone shown in Fig. 3. From the temperature contour plot, we can get the precise thermal properties of the pulse tubes and from the wave speeds information we can know the port timing and port positions.

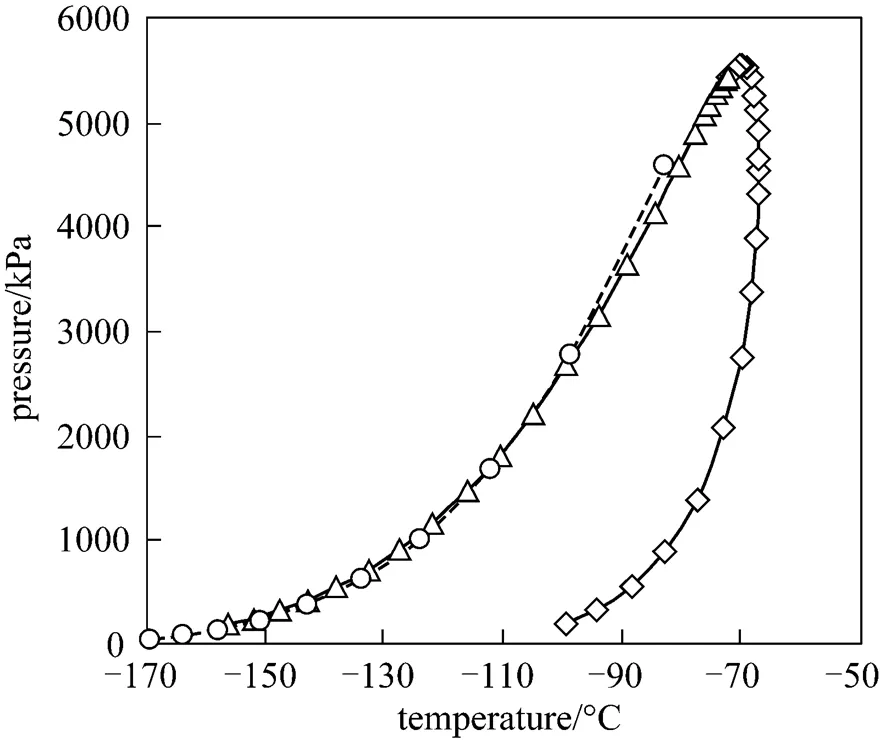
Figure 6 Envelope line of natural gas in pressure-temperature diagram (Natual gas mass fractions: C1-87.5%, C2-5.62%, C3-2.13%, C4-0.034%, C5-0.016%, CO2-2.29%, N2-2.41%)

◇ NG dew point;△ NG bubble point;○ C1bubble/dew point

Figure 7 Contour plot of temperature in-diagram based on real and ideal models

Table1 Wave speed (m·s－1) of natural gas fromPeng-Robinson EoS at different pressure ratios

Table 2 Temperature (K) of each zone (in Fig.3) byPeng-Robinson EoS at different pressure ratios

4 CONCLUSIONS

Flow of high molecular weight gases or gas mixtures that in the vicinity of saturated vapor line shows no classical patterns. A flow model coupled with Peng-Robinson state of equation other than perfect gas has been used to analyze the real flow in pulse tubes of GWM or PER. The calculation results have shown more precise behavior of various discontinuities. And a more reliable wave diagram is achieved to guide designing. With the help of real gas flow results, we have solved the offset design problem when using RTS in natural gas industry.

Nomenclature

c,critical parameters

sound speed, m·s－1

total energy, J·kg－1

,cartesian flux vector

specific internal energy, J·kg－1

precondition Jacobian matrix

specific enthalpy, J·kg－1

igspecific enthalpy at constant density of ideal gas, J·kg－1

thermal conductivity, W·m－1·K－1

pressure, Pa

primitive variable vector

gas constant, J·kg－1·K－1

diffusive matrix

rreduced temperature, K

,fluid speed inanddirection, m·s－1

(r) function of reduced temperature

ratio of specific heat capacity

viscosity, Pa·s

density, kg·m－3

specific volume, m3·kg－1

eccentric factor

1 Cramer, M.S., Nonclassical Dynamics of Classical Gases, Nonlinear Waves in Real Fluid, Springer Press, New York, 91-145 (1991).

2 Bober, W., Chow, W., “Nonideal isentropic gas flow through converging-diverging nozzles”,., 112, 455-460 (1990).

3 Aungier, R.H., “A fast, accurate real gas equation of state for fluid dynamic analysis applications”,., 117, 277-281 (1995).

4 Brown, B.P., Argrow, B.M., “Nonclassical dense gas flows for simple geometries”,., 36 (10), 1842-1847 (1998).

5 Thompson, P.A., “A fundamental derivative in gas dynamics”,., 14 (9), 1843-1849 (1971).

6 Hoffren, J., Talonpoika, T., Larjola, J., Siikonen, T., “Numerical simulation of real-gas flow in a supersonic turbine nozzle ring”,.., 124, 395-403 (2002).

7 Brown, B., Argrow, B., “Application of Bethe-Zel’dovic-Thompson fluids in organic Rankine cycle engines”,.., 16 (6), 1118-1123 (2000).

8 Merkle, C.L., Sullivan, J.Y., Buelow, E.O., Venkateswaran, S., “Computation of flows with arbitrary equation of state”,., 36 (4), 515-521 (1998).

9 Cirri, M., Adami, P., Martelli, F., “Development of a CFD real gas flow solver for hybrid grid”,...., 47, 931-938 ( 2005).

10 Chandrasekar, D., Prasad, P., “Transonic flow of a fluid with positive and negative nonlinearity through a nozzle”,., 3 (3), 427-438 (1991).

11 Cramer, M., Best, L., “Steady, isoentropic flows of dense gases”,., 3 (1), 219-226 (1991).

12 Cramer, M., Kluwick, A., Watson, L., Pelz, W., “Dissipative waves in fluids having both positive and negative nonlinearity”,.., 169, 323-336 (1986).

13 Cinnella, P., “Roe-type schemes for dense gas flow computations”,., 35,1264-1281 (2006).

14 Choi, J.Y., Oh, S.J., Jeung, I.S., “Correction of Roe’s approximate Riemann solver for real gas equation of state”, AIAA 2002-3293 (2002).

15 Brown, B., Argrow, B., “Two-dimensional shock tube flow for dense gases”,.., 349, 95-115 (1997).

16 Peng, D.Y., Robinson, D.B., “A new two-constant equation of state”,...., 15 (9), 59-64 (1976).

17 Starling, K.E., Han, M.S., “Thermo data refined for LPG (14) Mixture”,, 51 (5), 129-132 (1972).

18 Li, D., Sankaran, V., Lindau, J.W., Merkle, C.L., ”A unified computational formulation for multi-component and multi-phase flows”, AIAA 2005-1391 (2005).

19 Chima, R.V., Liou, M.S., “Comparison of the AUSM+ and H-CUSP schemes for turbo machinery applications”, NASA-TM 212457 (2003).

20 Liou, M.S., “A sequel to AUSM: AUSM+”,..., 129, 364 -382 (1996).

21 Liou, M.S., Steffen, Jr., C.J., “A new flux splitting scheme”,..., 107, 23-39 (1993).

2009-02-19,

2009-10-13.

* To whom correspondence should be addressed. E-mail: daiyq@chem.dlut.edu.cn