基于流量特性的调节阀阀芯曲线智能拟合*

李战明，王云峰,2，袁占亭

(1.兰州理工大学电气工程和信息工程学院，甘肃 兰州 730000)

在浮选过程中，浮选槽液位控制是浮选生产中的一个重要环节，其输入输出流量的大小及调节阀的控制等各影响因子之间的关系错综复杂, 又相互影响, 是一种复杂的非线性关系, 用传统的分析方法难以进行模拟。由于神经网络模型(Neural Network Model)具有对复杂对象、糊信息分析与建模的优势[1], 本文提出了基于神经元网络技术的软测量方法，在基于过程补余量算法中，引入利用不同形状的反馈凸轮片产生不同非线性来改变控制阀的原有流量特性，结合比例系数μi得到具有线性流量特性的不同调节阀曲线函数，最后通过仿真不同调节阀阀芯曲线函数给控制带来的影响，得到了适合大型浮选机浮选槽调节阀阀心曲线函数的建模和优化过程。

如今由于全球经济发展对矿物原料质量、数量要求的不断增长和矿产资源的品味越来越贫，大型浮选设备在矿物加工领域的作用和重要性日益突出，国内外各研究机构和公司纷纷加强了开发和研究工作[2-3]。金川集团公司自主研发了我国第一台160m3大型充气机械搅拌式浮选机，并配备了液面自动控制系统和充气量自动控制系统[4]，该系统对浮选槽液位控制效果的好坏直接影响到精矿品位和回收率的工艺指标的优劣[5]。

1 神经网络软测量模型的建立

由于出口阀门流量测量滞后较大且很难通过传感器直接进行测量，采用软测量技术提供估计值，为浮选槽液位优化控制与决策提供重要信息。

1.1 神经网络的选择

1985年美国MIT的PDP小组提出BP模型是近年来应用最广泛的网络之一[6]。通过对各种神经网络建模和函数逼近能力的评价，结合流体是液体时其惯性大的特点，选用BP网络为建模用神经网络。

1.2 神经网络模型的建立

图1 软测量的结构图

2 基于过程补余量算法

浮选槽液位的控制，受浮选槽入口矿液流量、浮选槽容积以及出口调节阀阀门开度调节等因素的制约，液位变化的过程是与入口流量和出口流量相关的过程[8]。不失一般性，设定控制作用为控制过程的流入量Uc，称为控制量；流出量由负荷需求UL决定；被控参数只影响流出量，其影响程度为1/K，称K为过程通道的增益[9]。根据过程的储存特性，过程的储存量可表示为：

(1)

其中SU为过程的储存量，y是被控参数。

对储存量及参数的变化给出如下定义：

(2)

其中ΔSU称为过程储存量的补入量，简称补入量；Δy是对应于ΔSU的被控参数调整量。ΔSU>0，称正补入；ΔSU<0，称为负补入。

3 满足调节阀理想流量特性设计

对于阀的流量特性，当阀前后压差一定时的流量特性称为理想流量特性或称固有流量特性[10]，如图2所示。

图2 理想流量特性

3.1 理想流量特性与目标补入量之间的关系

线性流量特性是指调节阀的相对开度与相对流量为直线关系：

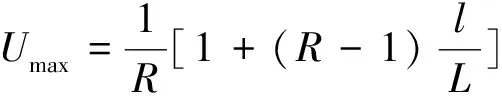
(3)

其中R为半径，L为行程，Umax为最大流量，UL为行程为L时的流量，l为实际行程。结合基于过程补余量算法[11]，得到浮选过程中流量符合线性特性的余量与调节阀有关参数的关系式：

·Umax

(4)

其中Ji+1为该状态下目标补入量，Ri为该时刻调节阀阀芯半径，li为该时刻调节阀实际行程。

3.2 神经网络调节阀曲线拟合

图3 BP神经网络结构

(5)

输出单元每产生一个实际的输出向量时，用期望输出与实际输出之差修正网络权值。权值修正采用δ学习规则，权值wij取(-1，1)之间的随机数。然后求出不同开度下半径所对应的行程，进而得到半径与行程相应的序偶对(Ri,li)，对该序偶对按半径由小到大排序，得到有序的序偶对(Ri',li')，最后对该序偶对进行神经网络调节阀曲线拟合，可得到任意精度拟合曲线：

Ax2+Bxy+Cy2+Dx+Ey+F=0

(6)

3.3 比例系数μi

根据伯努利方程[12]：

ρυ2=常数

(7)

其中P代表压强，ρ代表流体密度，υ代表流体速度。在实际应用时，由于理想流量特性已经畸变为工作流量特性。在忽略摩擦及热交换情况下，对于不可压缩流体定常流动，应用式(6)拟合出的阀芯曲线函数，我们可以得到理想静态状况下，调节阀从一种状态变化到另外一种状态时体积的变化率μi：

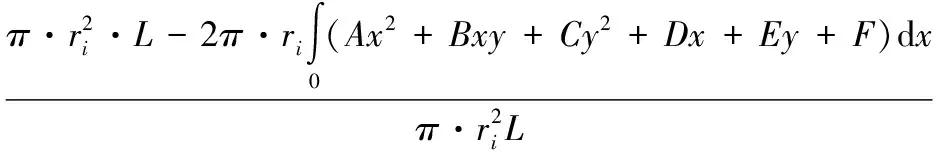
(8)

由于阀芯从一种形状变为另外一种情况，导致在同等行程下，阀芯半径发生了变化，相应地流量开度也发生了变化，这里用体积的变化率μi值来对阀芯半径进行修正。下面是对浮选槽排矿时调节阀在不同开度和行程下神经网络拟合后的各采样点流速的修正：

(i=0,1,…,n)

(9)

其中υ1=0，n为采样点数目，L为行程，g为重力加速度。浮选槽中流体，浓度、流量和压强等时刻都在发生变化，修正后的流速可以减小误差带来的影响。

4 实验仿真

(1)利用结论，结合现场工艺及设计要求，基于神经网络软测量技术，求出反馈凸轮片应产生的非线性作用，并且应用μi值进行修正，可分别计算出调节阀不同行程所应对应的开度，表1给出了一种情况下行程为li时开度的对应值Ri。

表1 li的对应值Ri

(2)对表1中的采样点，应用文中的神经网络软测量的方法进行神经网络曲线拟合：

y=-5.469 7x2-8.297 3e-0.16x+0.46

(10)

(3)满足线性流量特性的调节阀曲线。

图4中给出了经神经网络软测量计算拟合后调节阀的3种不同函数曲线，它们均在各自不同的开度和行程状态下可以完全满足线性流量特性的设计要求。但是，通过继续研究，通过现场跟踪检测，图5给出了调节阀阀芯采用3种不同函数曲线时浮选槽液位的变化情况，当调节阀阀芯为抛物线函数曲线时浮选槽液位变化最小，有利于浮选槽的液位稳定；同时，从仿真应用不同调节阀阀芯的控制系统中，图6给出了其相应控制系统的阶跃响应曲线，当阀芯为抛物线函数曲线时其控制效果最佳。

5 结 论

在金川有色金属公司选矿厂进行的工业试验表明：作为我国目前单槽容积最大的浮选设备液面控制系统配备的调节阀，达到了工艺设备的要求，对阀芯的大小和形状等有关参数与液面稳定方面的相关性进行了探讨，为我国研究开发大型浮选机各项技术的本土化，具有自主知识产权等，奠定了良好的科学理论依据。

图4 三种不同函数曲线

图5 液位变化情况

图6 阶跃响应曲线

参考文献：

[1] 王兆礼, 陈晓宏, 李艳.基于BPNNSI的多年平均水面蒸发量插值方法[J].中山大学学报:自然科学版,2007,46(1):114-115.

WANG Zhaoli;CHEN Xiaohong，LI Yan.Yearly mean pan evaporation interpolation method based on back propagation neural network model[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2007,46(1):114-115.

[2] 许荣华.硫化镍及硫化铜镍矿石选矿概述[J].昆明理工大学学报,2000(4):16-19.

XU Ronghua. Brief review on separtion of nickel sulfide ores and nickel-copper sulfide ores[J]. Journal of Kunming University of Science and Technology,2000(4) :16-19.

[3] 王碧善.国外大型浮选机的研制与应用[C].大型浮选机学术研讨会,1988:17-27.

[4] 沈振昌,刘振春.KYF-50充气机械搅拌式浮选机研制[J].矿冶,2001(3):31-36.

SHEN Zhengchang,LIU Zhenchun. Development of KYF-50 pneumo-mechanical flotation machine[J]. Beijing General Research Institute of Mining and Metallurgy,2001(3):31-36.

[5] 黄开国,陈万雄.一种低品位镍矿石的浮选工艺[J].中国有色金属学报,1999,9(3):601-605.

HUANG Kaiguo, CHEN Wanxiong. A flotation technique for low grade nickel ore[J].The Chinese Journal of Nonferrous Metals, 1999,9(3):601-605.

[6] 罗中良,麦宜佳,余剑峰.基于多传感器的神经网络模式识别方法[J].中山大学学报:自然科学版,2001,40(5):21-24.

LUO Zhangliang; MAI Yijia; YU Jianfeng.Method of model identification using neural network network based on multi-sensor[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2001,40(5):21-24.

[7] 金以慧,王诗宓,王桂增.过程控制的发展与展望[J].控制理论与应用,1997,14(2):145-151.

JIN Yihui; WANG Shifu; WANG Guizeng. Developments and prospects of process control[J]. Journal of Control Theory and Applications,1997,14(2):145-151.

[8] BERKAN R C. Advanced automation concepts for large scale-systems[J].IEEE Control Systems Magazine,1991,11(5):4-8.

[9] 朱国瑜.过程补入量与仿人智能控制.第二届全国智能控制专家讨论会论文集[C].清华大学,1994:481-486.

[10] 周其鉴.仿人智能控制器[J].中国仪器仪表,1993(2):5-9.

ZHOU Qijian. Human-simulated intelligent controller[J].China Instrumentation,1993(2):5-9.

[11] 柏建国,胡可剑.补偿纯滞后过程的新方法──智能采样调节[J].化工自动化仪表,1989(5):23-27.

BAI Jianguo,HU Kejian. A new method on compensation for time delay process-regulation on intelligent sampling[J].Control and Instrument in Chemical Industry,1993(5):23-27.

[12] 蔡武昌,孙淮清,纪纲.流量测量方法和仪表的选用[M].北京：化学工业出版社.2004:301-302.