面向资源调度的矩阵规范化方法研究*

周建涛，陆海燕，叶新铭

(内蒙古大学计算机学院，内蒙古 呼和浩特 010021)

计算机支持的协同工作是基于大规模分布式系统的重要应用，其中资源调度是非常基础的问题，在资源调度中又存在大量的多属性决策问题。例如，在动态、分布、异构、自治的网格环境下，用工作流技术构建复杂网格应用，当执行某个具体任务时，网格中可选择的满足任务需求的执行资源也许并非一个，可能有成百上千个。而在考量各备选资源时，除了完成任务的功能性需求(如：时间)，还可能考虑用户定制的非功能性需求，如完成任务所需成本、资源的信誉度及服务质量等。然而，各因素在其中发挥的作用不一样，相当于有不同的权值分配。在复杂系统中研究资源调度就是一类多属性决策问题，其研究是现代决策科学的重要内容，一直是国内外研究界和工业界感兴趣的课题，具有一定的重要性和现实意义。

1 背景知识

本节首先介绍需要用到的背景知识。

在一个多属性决策(Multi-Attribute Decision Making， MADM)问题中，属性是反映对象之间的一种关系的指示量，其量化技术的合理性直接影响到决策的效果[1]，因此属性的规范化技术是多属性决策问题的基础。属性之间一般都没有统一的度量标准，并且还存在一定的矛盾性，即对各属性的期望值是不同的甚至是相反的。具体来说，一方面各属性的单位不同、量纲不同、数量级不同；另一方面，属性还可分为效益型和成本型等不同类型。因此，对于一个已知决策矩阵的多属性决策问题，在求解各属性权值及各备选资源综合实力排序之前，都需要消除属性的量纲、数量级和属性类型对决策结果的影响，也就是说，需要对各属性值进行规范化处理。其实质是利用数学变换把量纲、性质各异的属性值转化为可以综合处理的“量化值”。一般是把各属性值统一变换到区间[0,1]上。规范化的目的在于获得可比的尺度。

下面，再将如上提到的决策距阵和属性类型分别进一步介绍。

属性类型一般有效益型、成本型、固定型、偏离型、区间型、偏离区间型等。实际中用得最多的属性是效益型属性和成本型属性。以往的资源调度也常采用效益型和成本型两种属性类型。效益型属性是指属性指越大越好的属性；成本型属性是指属性值越小越好的属性。它们都以最终处理后的数据大小来判断数据优劣，即数据值越大，数据质量越优，反之亦然。既然在同一个多属性决策问题中，对各属性的期望值不同甚至相反，而最后都要以最终结果值的大小反映值的优劣，则不可能用一个处理公式进行统一处理，而应该将各属性按类型进行划分，再施以不同的处理公式。在文章后续章节的介绍中，将用由0，1元素组成的Pflag向量来表示各属性的类型，属性为成本型，对应在Pflag中的元素为1；属性为效益型，对应在Pflag中的元素为0。Pflag向量长度等于属性的个数m。

2 决策矩阵的规范化方法

由于决策矩阵中各列分量的数值大小不一，因此，考虑数据处理的公平性和独立性，需要在决策矩阵参与运算之前将其进行规范化处理。本节首先介绍三种规范化处理方法。

在资源调度等多属性决策问题中[2-5]，决策矩阵的规范化多采用标准0-1规范化处理和一般规范化处理方法。而在Web工作量描述中，聚类算法在计算欧式距离前对原始数据进行规范化处理时，常使用ZSCORE规范化处理技术[6]。文章将这种方法也引入到资源调度问题中进行多属性决策前的矩阵预处理，并对该方法进行了改进。

2.1 标准0-1规范化处理方法

该方法的基本思想是将最好的属性值规范化为1，将最坏的属性值规范化为0，其余属性值采用线形插值的方法得到规范化值。

1)效益型的决策属性：将最大属性值规范化为1，最小属性值规范化为0，利用插值法得:

,i=1,…,n

(1)

2)成本型的决策属性：将最小属性值规范化为1，最大属性值规范化为0，利用插值法得:

,i=1,…,n

(2)

Zij是规范化后的属性值，其中

,。

在标准0-1规范化处理方法中，规范化后的属性值都转换到[0，1]闭区间，最优的数值转换为1，最劣的数值转换为0，但变换前后的数值不成比例关系。由于它具有简便的变换式和良好的特性，使之成为目前多属性决策及综合评价中用得最多的规范化方法。

2.2 一般规范化处理方法

该方法的基本思想是将最好的属性值规范化为1。与标准0-1规范化方法不同的是，对于效益型和成本型属性，变换前后的属性值成比例关系。

对于效益型的决策属性的处理式是:

(3)

对于成本型的决策属性的处理式是:

(4)

2.3 Z SCORE规范化处理方法

ZSCORE是利用了各个属性测量值的平均值和标准差的一种变换，可用来避免因属性的相对取值和范围大不相同而导致结果自然增长的问题，变换结果使得参数与单位无关。对于一个给定参数的ZSCORE计算如下：

(5)

属性类型有成本型和效益型，不同的属性有不同的量纲和单位，为了避免对后续决策计算带来不良影响，在决策之前需要消去各属性的量纲，即非量纲化，仅用数值的大小反映属性值的优劣。这样，仅用(5)式对所有属性进行统一处理，就没办法满足属性多种类型的需求，因此把(5)式根据成本型和效益型的属性特征分别进行改写。

对于效益型的决策属性的处理式是：

(6)

对于成本型的决策属性的处理式是：

(7)

这样，无论是成本型属性，还是效益型属性，只需看计算后的结果即可做出决策判断，结果越大说明属性值越优。

3 实验与分析

本节将上节介绍的三种规范化方法作用于多属性决策领域中的同一个资源调度实例的决策矩阵，最后通过实验数据进行各方法间的分析比较。

3.1 实验简介

实验在Windows XP的操作系统环境下，使用Matlab 7.0数学软件工具进行设计和开发。实验开发所涉及的主要函数如下：

(1)标准0-1规范化处理函数Standlize(X,Pflag)

① 输入：决策矩阵X，各属性的标志数组Pflag；

② 操作：以列为单位，对决策矩阵X的每一列向量求出最大值和最小值，分别保存至列最大值和最小值数组，然后按照公式(1,2)，对每列元素进行计算；

③ 输出：矩阵Z及程序运行时间。

(2)一般规范化处理函数Standlize1(X,Pflag)

① 输入：决策矩阵X，各属性的标志数组Pflag；

② 操作：以列为单位，求X矩阵每一列向量的最大和最小值，分别保存至列最大值和最小值数组，然后按照公式(3,4)，对每列元素进行计算；

③ 输出：矩阵C及程序运行时间。

(3)ZSCORE规范化处理函数Zscore(X,Pflag)

① 输入：决策矩阵X，各属性的标志数组Pflag；

② 操作：以列为单位，求X矩阵每列的平均值和标准方差，分别保存至列平均值和标准方差数组，然后按照公式(6,7)，对每列元素进行计算；

③ 输出：矩阵U及程序运行时间。

3.2 举例

设在某资源调度问题中，有4个备选资源，即R=(R1,R2,R3,R4)，以时间、质量、成本和服务4个属性，即P=(Rt,Rq,Rc,Rs)来综合考量各备选资源的整体实力。计算过程如下。

(1) 首先输入决策矩阵X及属性的标志数组Pflag=[1 0 1 0]。X矩阵的横向量为(Rt,Rq,Rc,Rs)，纵向量为(R1,R2,R3,R4) ，具体数值如图1中所示。

(2) 经过标准0-1规范化处理Standlize(X,Pflag)之后，得到矩阵Z，具体数值如图1中所示。处理时间为0 s。

(3) 相同的输入决策矩阵X及属性标志数组Pflag，经过一般规范化处理Standlize1(X,Pflag)之后，得到矩阵C，具体数值如图2中所示。处理时间为0 s。

(4) 相同的输入决策矩阵X及属性标志数组Pflag，经过Z-score规范化处理后，得到矩阵U，具体数值如图3中所示。处理时间为0.07 s。

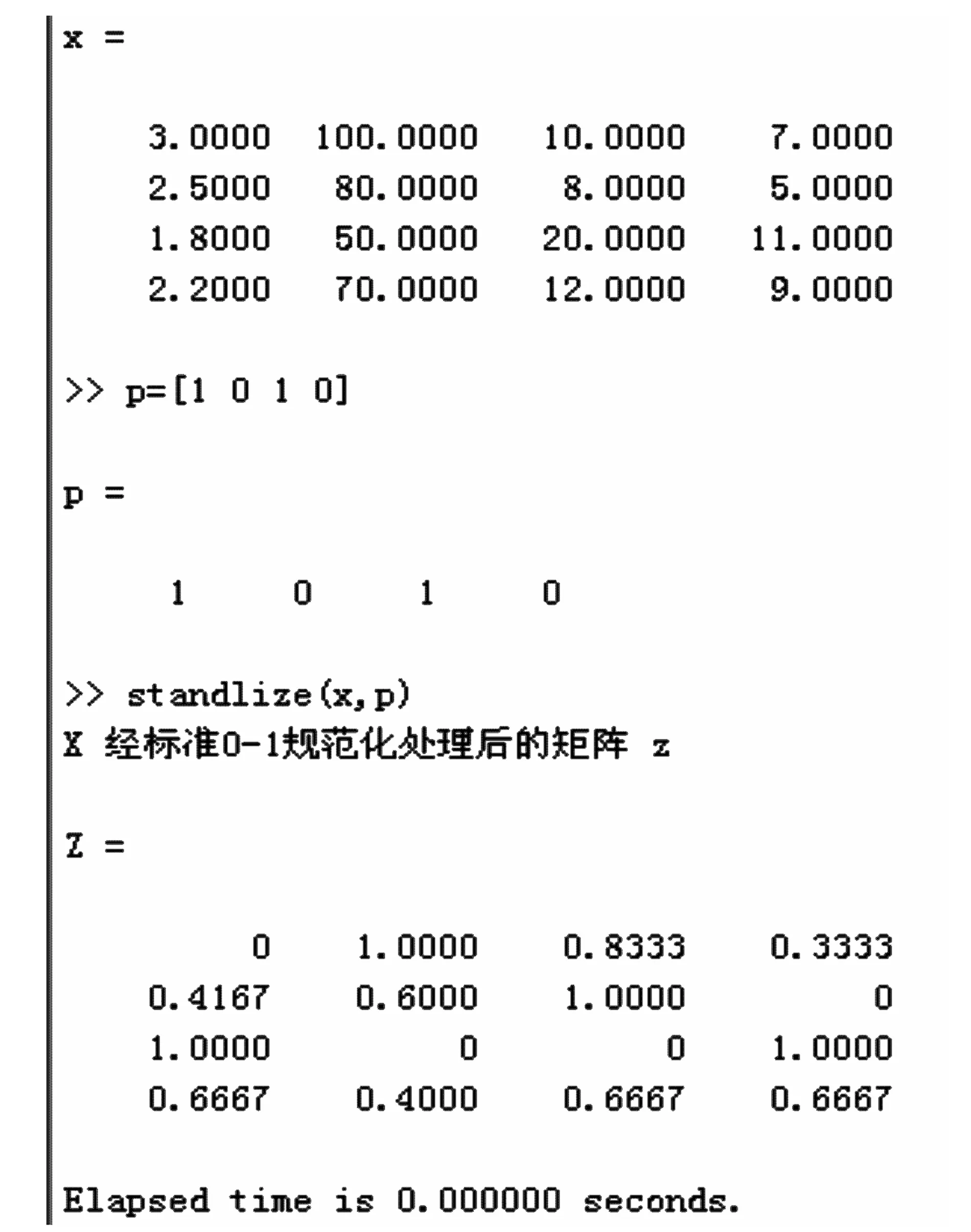
图1 标准0-1规范化方法处理结果

3.3 分析与比较

通过上节的计算，分别得出标准0-1规范化说明：以上的处理时间输出格式采用系统默认格式，仅保留6位小数，不过已足够用于对这三种方法的分析和比较。

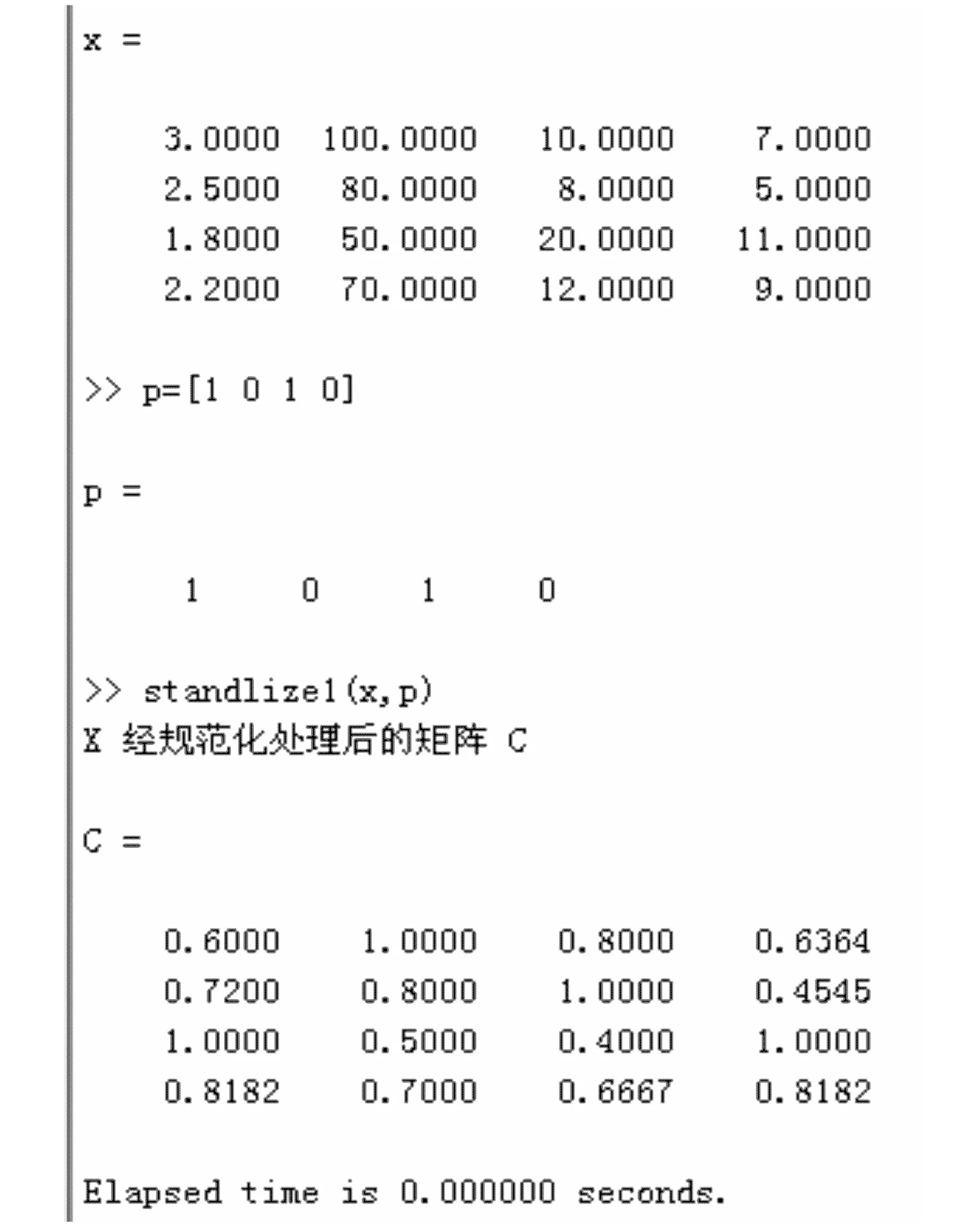
图2 一般规范化方法处理结果

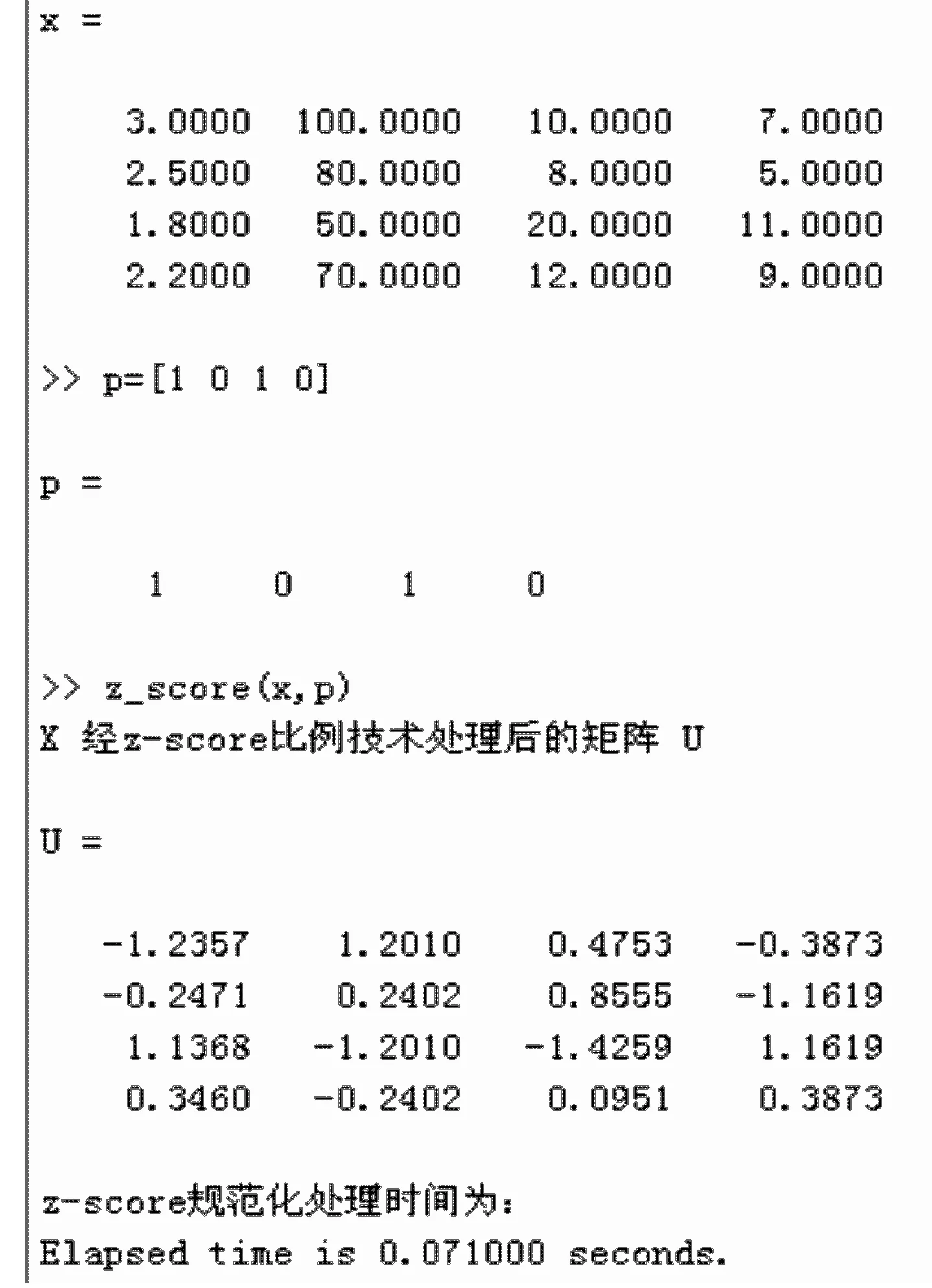
图3 Z-score方法处理结果

方法，一般规范化方法及Zscore方法作用于同一决策矩阵X后的结果矩阵及所用的计算时间，以下将会从数据和时间两方面对这三种规范化方法进行分析比较。

3.3.1 规范化结果比较 表1和表2是使用三种方法成本型和效益型属性进行规范化后结果数据的比较。

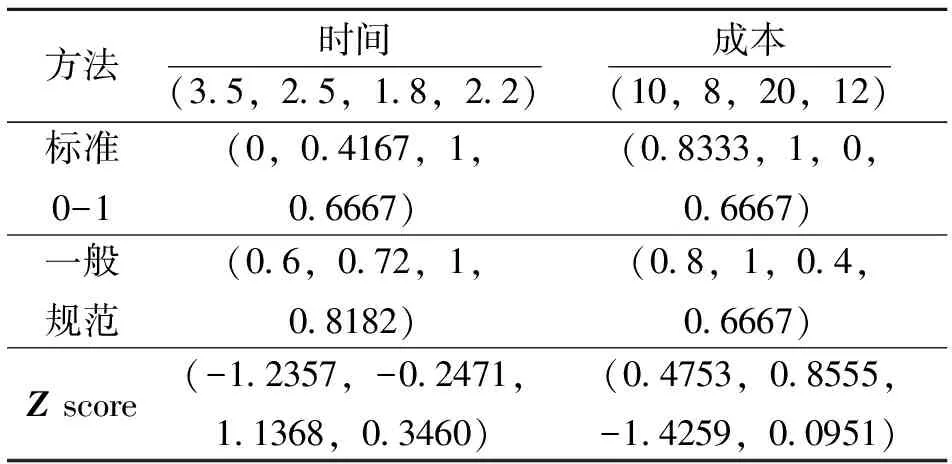
表1 成本型属性规范化结果比较

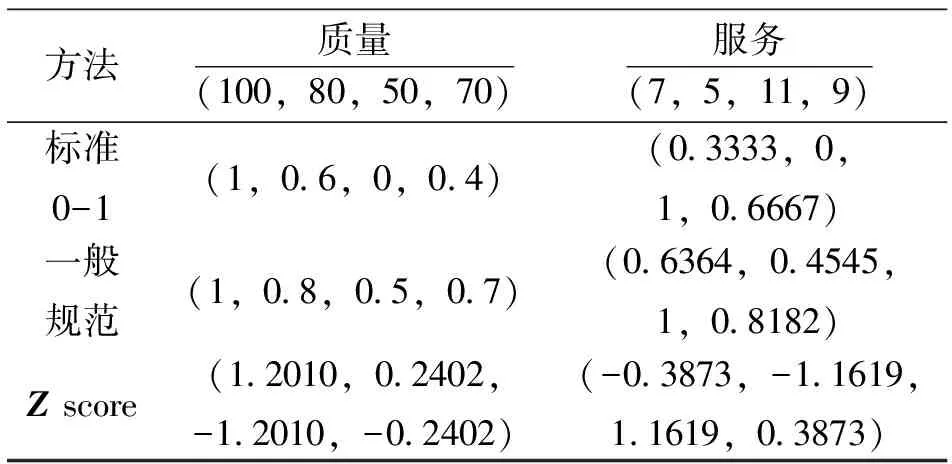
表2 效益型属性规范化结果比较

标准0-1规范化处理后，X矩阵的每列值都处于0-1之间。对成本型QoS来说，值越小处理后结果越大，对效益型QoS来说，值越大处理结果越大。结果最小可到0，最大可到1，其余结果在0-1开区间分布；

一般规范化处理后，X矩阵的每列值都也都处于0-1之间，但是不会出现0元素；

经Zscore比例技术处理后，虽然结果分成本和效益两类也遵从上述的规律，但是每列的处理值中数值有正有负，而且每类数据的最大和最小值相差结果大于1，数据不规律，对日后减法等操作带来处理复杂度。

3.3.2 规范化处理时间比较 标准0-1规范化、一般规范化、Zscore规范化处理时间分别为0.000、0.000、0.070 s。

标准0-1规范化处理技术涉及到求每列数据的最小、大值，都可以用Matlab的内部函数实现，接着作减法和除法运算，从图4中可以看出这些操作用时少，低于10-3数量级，因此整个算法的耗时为0 s；

图4 standlize(X,Pflag)耗时分析

一般规范化处理技术涉及到求每列数据的最小、最大值，但较标准0-1规范化来说，少了减法操作，从图5中可以看到，这种算法处理的时间也很少，低于10-3数量级，算法的总耗时也为0 s；

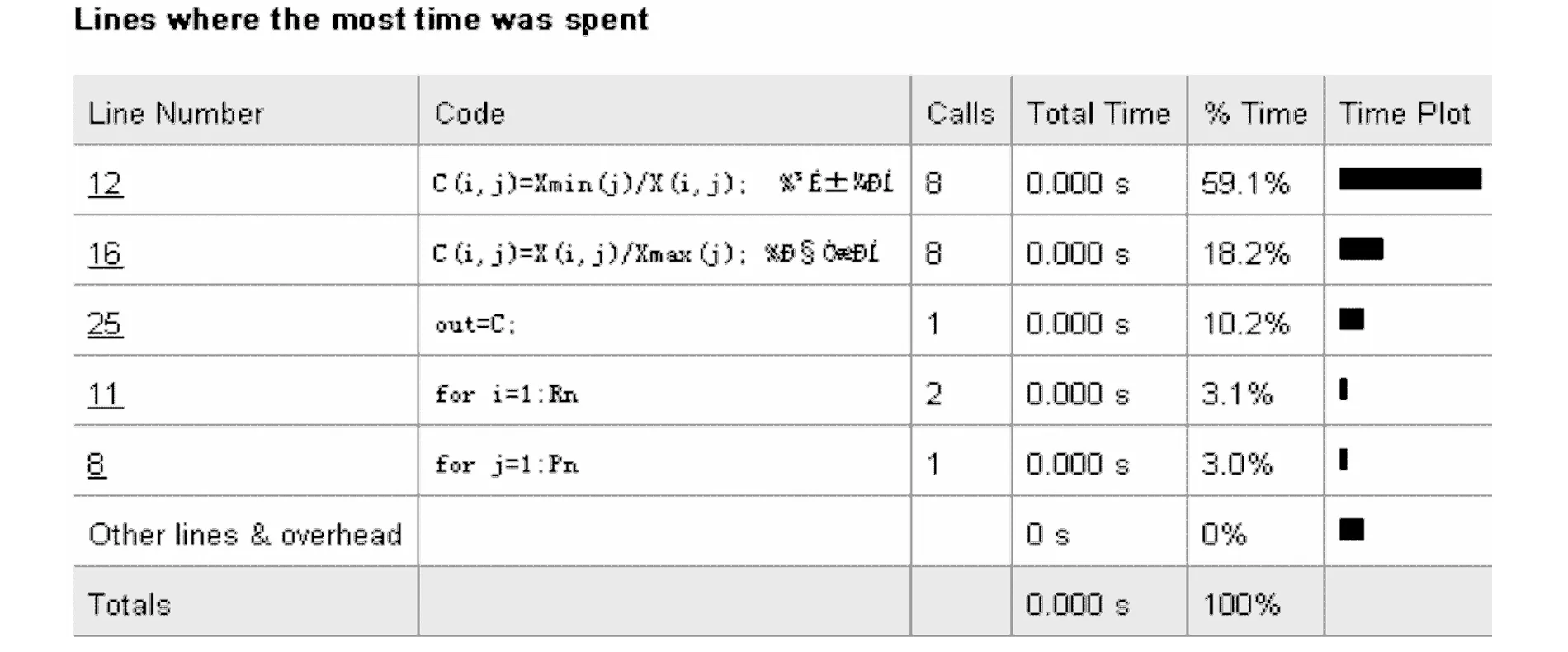
图5 standlize1(X,Pflag)耗时分析

Zscore比例技术涉及到求每列数据的平均值和标准差，虽然也由Matlab的内部函数实现，但这两个运算的复杂度远远超过求最小、最大值的运算方法，如图6，它们的运算时间都大于10-2数量级，因此消耗了算法的大部分时间。在本例中，Zscore处理时间为0.07 s；

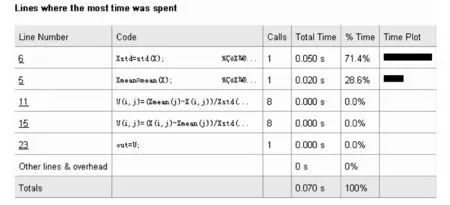
图6 Z-score(X,Pflag)耗时分析

综上所述，不论从处理后的数据质量还是从时间，标准0-1规范化和一般规范化的方法较Zscore来说性能更优，更适用于资源调度的计算工作。而标准0-1规范化和一般规范化处理的时间相差不大，数据元素也都在0和1之间，但标准0-1规范化后的矩阵每列必有一个0，这可以减轻后续计算的运算量。所以标准0-1规范化处理方法为这三种资源调度决策矩阵的规范化方法中的最优方法。

4 结 语

复杂分布式环境中的资源调度问题大都涉及到多属性决策问题，而多属性决策的基础问题是各属性的量化问题，即决策矩阵规范化问题。对于此类问题，本文做了如下工作：

(1)集中讨论和比较了三种规范化处理方法，分别是标准0-1规范化方法，一般规范化方法，以及z score规范化方法。

(2)对Zscore运算式进行了改进，使之能适用于多属性决策运算。

(3)最后，以实验数据来对比分析这三种规范化方法在资源调度中的处理效果。实验结果表明，标准0-1规范化处理方法是在可归属为多属性决策问题的资源调度问题中，用于矩阵规范化处理较理想的方法。

参考文献：

[1] 张尧庭．指标量化、序化的理论和方法[M]．北京：科学出版社，1999: 22-53.

[2] 刘丽兰，余涛，施战备．制造网格中基于服务质量的资源调度研究[J]．计算机集成制造系统，2005，11(4): 475-480.

LIU Lilan, Yutao, SHI Zhanbei. Quality of service management system in manufacturing grid[J]. Computer Integrated Manufacturing Systems, 2005,11(4):475-480.

[3] TANG Lei ,YANG Zhiyi, YU Zhiwen,et al. A quality-driven algorithm for resource scheduling based on market model on grid [C]. The 2nd International Workshop on Advanced Distributed and Parallel Network Applications (ADPNA 2007), in conjunction with the 36th International Conference on Parallel Processing (ICPP 2007) USA: IEEE Computer Society Press, 2007: 9-14.

[4] WANG Yingming, PARKAN Celik. Multiple attribute decision making based on fuzzy preference information on alternatives: Ranking and weighting[J]. Fuzzy Sets and Systems, 2005, 153(3): 331-346.

[5] XU Zeshui. On multi-period multi-attribute decision making[J]. Knowledge-Based Systems, 2008, 21(2): 164-171.

[6] MENASCé Daniel A, ALMEIDA V A F. Capacity planning for Web performance: metrics, models, and methods [M]. New Jersey:Prentice Hall PTR Prentice Hall,Upper Saddle River, 1998: 250-262.