对应，植树问题的灵魂

张秀清

一、初步感知规律

听写：圆、三角形、圆、三角形、圆、三角形。

师：这里有几个圆、几个三角形?圆与三角形的个数怎么样?接下去会画吗?(学生接着画)

师：怎么不画了?能画完吗?怎么办?

生：用“……”表示。

师：谁来解释一下“……”的意思?

生1：“……”表示有很多很多，画不完。

师：圆有多少个？三角形有多少个?

生：圆有无数个，三角形有无数个。

师：圆和三角形哪个多?

生：一样多。

师：为什么?

生2：都是无数个，所以一样多。

生3：圆和三角形是一组，所以圆和三角形一样多。

师：谁上来一组一组地画出来?(生画略)

师：圆和三角形是对应的，圆和三角形的排列是有规律的，有什么规律?

(引导学生观察两个圆中间一个三角形、两个三角形中间一个圆，发现圆和三角形是一一对应、间隔排列的，所以圆与三角形一样多)

师：我接着再画一个圆，圆和三角形的个数有什么关系?

生：原来一样多，现在圆比三角形多了一个。

师：用“对应”二字会说吗?

生4：圆和三角形原来是对应的，现在多了一个。

……

学生理解了间隔排列、一一对应后，再添加一个圆，在这种排列下，添加的圆没有对应的三角形，让学生感受到两端物体相同时两种物体之间的数量关系。植树问题中，如果两端都种树，树和间隔的对应关系就是上面三角形与圆的对应关系。

二、加深认识规律

出示例题(兔子与蘑菇、木桩与网、手帕与夹子图)

师：图中有哪些物体是间隔排列的?兔子与蘑菇有什么关系?(引导学生用“对应”二字说一说)

……

师：用圆代替柱子，用三角形代替网。

多媒体演示把三幅图合并成一幅图，如下：

○△○△○△……○△○△○

师：看到这幅图，你想到什么?

生1：圆和三角形是一一对应的，圆的个数比三角形多一个。

多媒体演示把最后的圆去掉，变为下图：

○△○△○△……○△○△

师：现在呢?

生2：圆和三角形是一一对应的，圆的个数和三角形一样多。

师：生活中有没有这样间隔排列的问题？

(学生举例，如会场坐椅的扶手、电灯等等)

师：马路边有25根电线杆，每两根电线杆之间有一个广告牌，一共有多少个广告牌?(生答略)

师：教室里男女同学的座位也有间隔排列的情况。每两个男生之间插一个女生，插了几个女生?(3个)

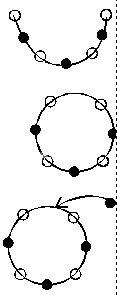
多媒体出示○●○●○●○，然后变成了弧形，如右图。

师：现在男生几个?(4个)女生几个?(3个)

多媒体把弧形变成圆形，如右图。

师：现在几个男生?(4个)几个女生?(3个)

最后多媒体动态显示在两个男生之间插入一个女生，如右图。(男生和女生同样多了)

这由“开”到“合”的过程，设计得实在太妙了!贲老师利用图形的变形，轻而易举地解决了物体“开”“合”不同排列之间的联系与区别。

感悟：

从以上教学过程中，笔者深深体会到我们的学生做“植树问题”为什么会出现那么多的错。

原因一：对“间隔”的含义理解不深刻。人教版教材没有“间隔排列”这样一节教学内容。二、三年级的“找规律”主要让学生感受排列组合的数学思想和有序思考的学习方法，到四年级教学“植树问题”时才出现“间隔”一词。一般教师对“间隔”一词的含义，教学时间花的较少，学生对“间隔”的理解也仅仅停留在“两点之间的一段距离”的认识上。苏教版教材专门安排了“间隔排列”的教学内容，使学生在大量感性认识的基础上，能更深层次地理解“间隔”的本质。贲友林老师精彩的教学设计，更是把“间隔排列”和“植树问题”有机地结合了起来。

原因二：我们以往总是把“植树问题”分成三类教学，通过一些实际例子让学生找到规律：两端都种树，棵数=间隔数+1；两端都不种，棵数=间隔数-1；一端种一端不种或封闭的时候，棵数=间隔数。这样教学，实际上是人为地把知识之间的内在联系割裂了，不但加重了学生记忆的负担，而且还容易混淆。

贲友林老师用对应的数学思想统领整节课，紧紧抓住间隔问题的本质就是对应问题进行教学。植树问题的三种情况实质上就是间隔排列的不同情况，因此植树问题的本质也是对应问题。当树和间隔一一对应，这时棵数与间隔数一样多；当树和间隔一一对应，最后还多出了一棵树，这时棵数就比间隔数多一；当间隔和树一一对应，最后树没有了，而间隔还有一个，这时树比间隔少一。封闭图形中的植树问题也是对应问题，此时棵数和间隔数正好一一对应。至于对应时“一对多”的情况，笔者认为，只要“一对一”理解透彻了，“一对多”只是举一反三的事情，不难理解。

总之，用对应思想统领植树问题，在整个教学过程中贯穿始终，就不必再分类型记规律，植树问题就不再那么难解决了。