舰船RCS整形设计中的电磁分析

宋东安 邢 芳 温定娥 张 崎

电磁兼容性国防科技重点实验室，湖北武汉430064

舰船RCS整形设计中的电磁分析

宋东安 邢 芳 温定娥 张 崎

电磁兼容性国防科技重点实验室，湖北武汉430064

减小舰船雷达散射截面（RCS）需要对舰船进行整形设计。本文从分析舰船典型结构——金属板的RCS与雷达波的入射角、频率及几何尺寸的关系出发，采用物理光学法导出了金属平板RCS与倾斜角的理论公式，确定了在单频点或多频点对平板进行雷达隐身设计的最佳倾斜角，通过具体实例说明了在舰船整形设计时，采用本文给出的计算公式可以对舰船的RCS和舱室容积进行折衷设计。结论对舰船雷达隐身设计具有指导意义。

金属板散射；舰船RCS；整形设计

1 引言

舰船雷达隐身是舰船全隐身技术中的重要一环。它是以降低舰船被敌方雷达或电磁探测设备发现为目的一种防御技术。目前，该技术已普遍应用于舰船总体设计中，并作为舰船的一项重要的战术、技术指标。由于舰船是一个外形复杂的电大尺寸的结构物，所以其雷达隐身设计较之飞机和其它目标而言要复杂和困难得多。但是，人们针对舰船的结构特点，在不断的实践中总结出了一些舰船雷达隐身设计方法和措施。通过采取这些措施，显著地降低了舰船的雷达信号特征值——雷达截面积（RCS），使舰船逐渐向隐身化发展。通过对舰船外形进行整形而减小其RCS目前是舰船雷达隐身设计中主要采取的一种技术［1，2］。该技术不仅适应的频段较宽，而且隐身效果良好。

舰船整形技术是利用金属平板散射电磁波的原理将入射的雷达波向一些无危险（或威胁）方向散射。对于舰船而言，主船体和上层建筑是舰RCS的主要贡献部分，因此通常采用一些平直金属板来构造这些部位，并倾斜布置以控制反射波的方向。然而在舰船总体设计阶段中，整形设计通常要考虑和兼顾与舱室容积的关系。倾角过大，虽可减小舰船的RCS，但同时也减小了舱室的容积而影响舱内设备的布置，反之亦然。以前通常是采用经验法来解决这个问题，例如文献［2］中给出了当频率为9.1 GHz，金属平板倾斜角为3°、5°、7°和10°时与RCS减少的关系。此关系虽可用于设计中，但有局限性，当频率或倾斜角改变时将不再适用。事实上，金属板的RCS不仅与雷达波的入射角、频率相关而且还与其的几何尺寸相关。本文将采用物理光学法对金属板的RCS进行理论分析，讨论了在不同的频率和不同的几何尺寸下，金属平板的RCS与倾斜角的关系。所得出的结论可以用于舰船雷达隐身设计的整形技术之中。

2 面散射基本理论

物理光学法也称为物理光学近似或面电流法［3-6］。该方法在分析面散射问题时是基于Stratton－Chu积分方程［7，8］，为了使该方程便于计算做了2个基本假定，其一在目标被照射面的每点局部电流密度和在一无限大相切平面上该点流过的电流密度相同；其二，目标任一部位的几何阴影在该阴影部位上产生电流为零，这就是说当电磁波正面照射金属板时，其背面将不产生电流。虽然这两种假设具有一定的局限性，但当散射方向偏离镜面反射方向不远时，该方法可给出令人满意的预测结果。在上述2个基本假设下，物理光学法给出的RCS计算公式为［9］：

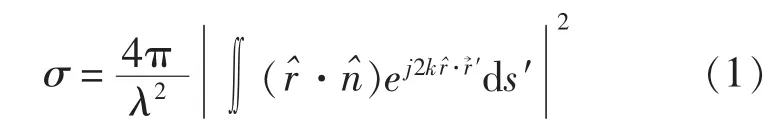
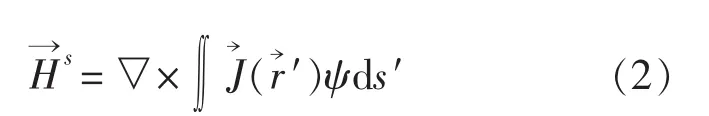
式中ψ为自由空间格林函数，上式右边的求导与积分无关，因此可移入积分号内：

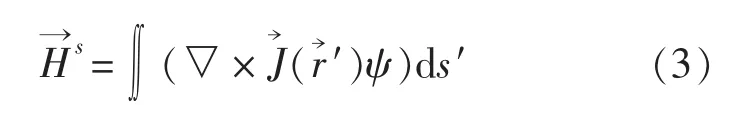
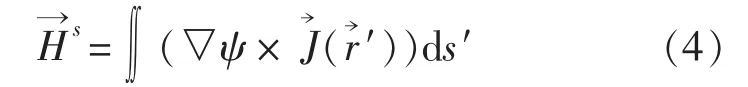
在远场近似条件下有：

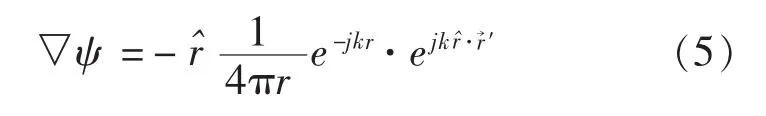
用磁场定义的RCS为［1］：

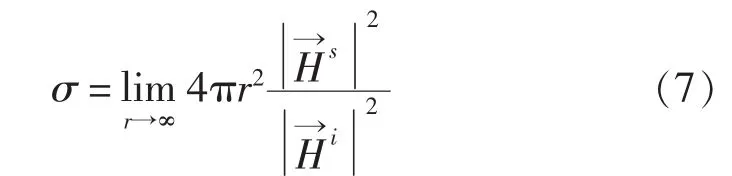
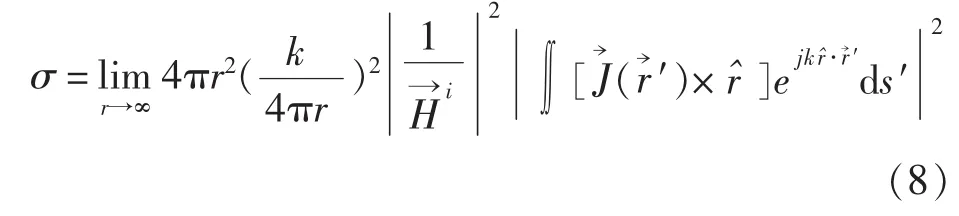
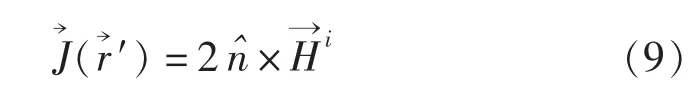
将式（9）代入式（8）并进行简化可得：

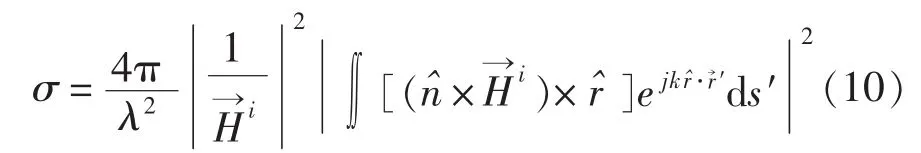
式中Hi为入射磁场的模，为入射磁场的方向矢量，为平面波入射的方向矢量，将式（11）代入式（9）可得：

式（12）即为目标在平面波任意入射时，在任意散射方向中的RCS计算公式，当我们只考虑目标的后面（或单站）散射时，则有：

3 分析与讨论

现代隐身舰船外形的特点是用若干个平直金属板构成，特别是上层建筑、桅杆和烟囱更是如此。设计者通过调整这些金属板的倾斜角来减小舰船在有威胁方向上的RCS。关于平板的散射特性已做了许多理论和实验上的研究工作［10，11］，但将这些研究成果用于舰船整形设计时还要做一些研究工作。下面我们运用式 （12）来分板平板的RCS随倾斜角的变化关系。如图1所示，金属板与垂直面的夹角（或倾斜角）为α。在图中建立了两个坐标系，一个是x′y′平面坐标系，坐标原点在金属板的几何中心，y′轴指向纸内；另一个是xyz立体坐标系；其原点、x轴和y轴与x′y′坐标系重合，z轴垂直金属板并且xyz 3轴方向满足右手螺旋定则。金属的长度在x方向为a；在y方向为b（图中没有注明）。下面我们利用图1中的坐标系对式（12）中的积分核进行简化运算：

图1 平面波入射金属板示意图

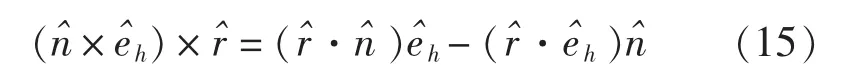
由于一般的雷达波为垂直极化，因此我们可假设入射平面波的磁场方向垂直纸面指向外部（h／），并且平面波的方向平行于xz平面，这样其反射波的方向也基本平行于xz平面。因此可认为（ˆ·ˆh）≈0；另外，当场点很远时，ˆ≈（ˆ0为原点O指向场点的单位矢量，用→0表示相应的距离矢量）0与z轴的夹角为θ，因此（·ˆ）≈（ˆ0·）＝cosθ。这样式（15）简化为：

式中的θ和φ为球坐标系中的角坐标。由图1可知平面波的入射方向与z轴的夹角为α，则：

上式表明由于斜入射，使平板上的电流相位在x′方向按线性律变化，但其幅值可认为是均匀分布。将式（16）～式（18）代入式（12）得：

对式（19）进行积分运算得：

在舰船整形设计时，我们主要关心平板在俯仰面（或图1所示的x′z平面）内的散射特性，因此可令φ＝0，式（20）可简化为：

上式表明，金属的散射特性与入射角、波长以及金属板的几何尺寸相关。式（23）与平板单站的RCS具有相同的函数形式，只是最大散射方向不在Z方向，而是偏离了一个角度。利用最大辐射条件可求出这个角度。令sinθ－sinα＝0；则sinθ＝sinα，α＝θ，这正是几何光学的结论，即反射角等于入射角。这说明利用平板的倾斜布置，可以将入射的主要电磁能量向无威胁方向反射。但还是有少量的电磁能量沿入射方向相反的方向（－）散射。在舰船整形设计中要尽量减小这个方向上的散射，下面我们将讨论这个问题。

设当倾斜角为αn时，沿－方向的散射最小，则令：

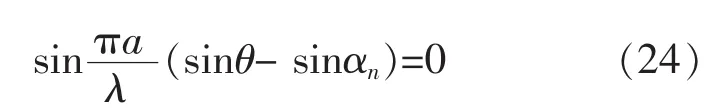
或

式中n取不等于零的整数。由式（12）可知αn＝－θ，代入上式可得：

上式右边的“－”号已被略去。n的含义是对应着散射方向图的第n个零点。同理我们也可求出在－方向产生旁瓣散射最大时的倾角αm，此时令：

可求得：

式中m取非零正整数，其含义是对应着散射方向图第m个旁瓣。式（26）和式（28）是我们设计平板倾角的理论依据。显然，当αn向αm变化时，平板沿－方向的散射则由小到大或反之，因此平板倾斜角设计的基本原则是应尽量接近αn或远离αm。需说明式（26）或（28）在用于单频或存在倍数关系的多个频点的隐身设计时可以获得非常好的效果。如果在一个宽且连续的频段上设计舰船的雷达隐身，将不可避免地出现满足式（28）的频点。这时我们要分析旁瓣散射大小与m的变化关系。由式（23）可以证明，第m个旁瓣最大散射的σm可按下式计算：

式中σ0为平板的散射最大值（即主瓣散射）。对上式进行归一化并取对数可得：

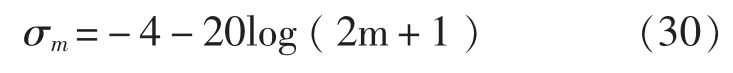
以上两式表明，σm随m的增大而减小。但在舰船整形设计时，m的值不能取得太大，否则对应的αn会太大，这样会减小相关舱室的可利用空间。另外，从表1可看出，当m很大时，σm（dB）减小的量值显著变小，基于这两点原因，在具体设计时，m的值不易取得太大或太小，应采取折衷的方法选取。下面将举例说明在舰船整形设计时，如何采用式（26）、（28）和（30）进行分析。

表1 σm与m的变化关系表

在某舰上层建筑弦侧边一块宽度为a＝1 000 mm的平板整形设计中，需确定该平板的倾斜角。所考虑的隐身频段≥2 GHz（即λ≤150 mm），要求σm（dB）＜－20 dB，由表1可知取m＝3，λ＝150 mm。将上述数据代入式（28）可求得，αm＝3＝31.7°；代入式（26）可求得αn＝3＝13°。按上述原则，该平板的倾斜角为13°，如果该倾斜角能满足相应舱室空间的要求即可。否则取m＝2进行再一次分析计算，这时只能要求σm＜－18 dB。另外，改变平板的宽度a也会影响倾斜角的设计。以上我们分析了频率低端的RCS。可以证明，一旦频率低端的整形设计满足要求，那么当频率升高时则一定满足要求。

4结论

本文基于面散射基本原理，对舰船RCS整形设计中如何合理选取平板的倾斜角进行了理论分析和讨论，指出在单频或存在倍数关系的多频点上进行雷达隐身设计时，采用本文给出的式（26）或式（28）可给出平板的最佳倾斜角。但是，实际上舰船的雷达隐身设计通常要考虑一个宽且连续的频段，这时可采用本文的结论进行合理的折衷设计。最后，通过一个简单的例子说明了在舰船整形设计时，如何采用本文给出的相应公式进行折衷设计和理论分析。本文给出的结论对舰船雷达隐身设计具有一定的指导意义。

［1］ 朱英富，张国良编著.舰船隐身技术［M］.哈尔滨：哈尔滨工程大学出版社，2003.

［2］ 克拉特E F.雷达散射截面——预估、测量和减缩［M］.阮颖铮，译.北京：电子工业出版社，1988.

［3］ 吴楠，温定娥.运用高频方法计算舰艇RCS［J］.中国舰船研究，2008，3（2）：77－80.

［4］ 徐云学，龚书喜.基于MATLAB的电大尺寸目标RCS计算系统研究［J］.电波科学学报，2007，22（2）：266－270，291.

［5］ 刘战合，黄沛霖，高旭，等.电大尺寸散射体的RCS计算方法研究［J］.沈阳航空工业学院学报，2007，24（1）：21－24.

［6］ 伍光新，邓维波，姜维，等.高频段飞机目标RCS分析［J］.电波科学学报，2008，23（3）：545－549.

［7］ 龚中麟，徐承和.近代电磁理论［M］.北京：北京大学出版社，1990.

［8］ GORDON W B.High frequency approximations to the physical optics scattering integral［J］.IEEE Transactions on Antennas and Propagation.1994，42（3）：427－432.

［9］ STUTZMAN W L，THIELE G A.Antenna Theory and Design［M］.John Wily＆Sons，Inc，1998.

［10］ SKOLNIK M I主编.雷达手册［M］.谢卓，译.北京：国防工业出版社，1978.

［11］ 张浩斌，马凯学，郭陈江，等.任意多边形导体板的高频散射分析［J］.电波科学学报，2003，18（1）：53－56.

The Electromagnetic Analysis in Ship RCS Plastics Design

Song Dong－an Xing Fang Wen Ding－e Zhang Qi
The National Key Laboratory of Eclectromagnetic Compatibility，Wuhan 430064，China

The radar cross－section（RCS）reduction needs applying plastics design to ship.In this paper，setting out from typical structures—metal plate，and discussing the relation of RCS with incident angle，frequency of radar wave，and geometry of metal plate，the formula，which characterizes the RCS of the plate with inclined angle，has been derived by physical optics theory.Through the formula，the optimal inclined angle can be determined at single frequency and multiple frequencies.Also，an example is presented to illustrate how to make a compromised design according to formulas considering stealthy of the ship and volume of the cabin.The results are significant to the stealthy design of ship.

metal plate scattering；ship RCS；plastics design

TN03

A

1673－3185（2009）03－52－04

2008-11-03

十一五预研支撑项目（6220100302）

宋东安（1958-），男，研究员。研究方向：电磁兼容设计、分析与实验研究。E-mail：EMCeditor@126.com