水下爆炸冲击载荷的一种新型算法研究

陈 娟 许永秋 姚熊亮 位 莎

1哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001 2浙江省台州市海事局，浙江 台州318000

水下爆炸冲击载荷的一种新型算法研究

陈 娟1许永秋2姚熊亮1位 莎1

1哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001 2浙江省台州市海事局，浙江 台州318000

近年来，越来越多的研究者都重视使用计算机的数值模拟对水下爆炸进行研究。水下爆炸包含了一系列复杂的物理过程，如大变形、高度非均匀性、可变形边界和自由表面。对于传统的基于网格的数值方法，水下爆炸问题的模拟是一项非常具有挑战性的工作。介绍了无网格光滑粒子流体动力学（SPH）方法在水下爆炸模拟中的应用，并且提出了处理固壁和物质交界面的算法，给出了水下爆炸过程具有代表性瞬间的压力分布、速度分布以及气泡的演变和脉动，为舰船水下爆炸冲击载荷的计算提供了一种新型有效的研究方法。

水下爆炸；冲击波；气泡；壁面反射

1 引言

舰船水下爆炸近场问题涉及水中冲击波的入射、透射、反射以及气泡的脉动等复杂物理现象，使得气、液、固态结构之间的瞬态相互作用强烈而复杂，因此，舰船近场水下爆炸结构动态响应问题还有许多问题有待研究和解决。然而对于传统的基于网格的数值计算方法，水下爆炸问题的模拟是一项非常具有挑战性的工作。一方面，由于存在大变形、运动物质交界面、可变形边界和自由表面等特性，使得基于网格的数值方法难以处理；另一方面，在整个水下爆炸过程中，高能炸药的起爆过程的复杂性和大尺度等问题使基于网格的方法面临更多的困难。

近年来，由于无网格技术的发展和应用日趋成熟，人们开始将无网格方法应用到可压缩多介质流的数值模拟中，如气泡上升［1，2］、深水强爆炸［3］、水介质缓冲［4］等问题。光滑粒子流体动力学（SPH）方法［5，6］具有无网格性质和拉格朗日粒子特性，它应用离散化的粒子来表示物质，能够很自然地对多介质流进行模拟，而且由于不受网格划分的限制，可以解决在基于网格的数值方法中由于高压、高能、大变形等导致网格畸变而计算崩溃的问题。因此本文用此方法对水下爆炸过程的机理进行研究，并且提出了处理固壁和运动物质交界面的点对点算法，旨在为舰船水下爆炸冲击载荷的计算提供一种新型有效的研究方法。

2 水下爆炸理论基础

水下爆炸是指在极短时间内，在水下的极小体积内或面积上发生极大能量转换的过程。水下爆炸大体可分为3个阶段：装药的爆轰、冲击波的产生和传播、气泡的形成和脉动。当炸药在水中爆炸时，其周围介质直接受到具有高温、高速、高压的爆炸产物作用。在装药和介质的界面处，爆炸产物以极高的速度向周围扩散，强烈地压缩着相邻的水，使其压力、密度、温度突跃式地升高，形成初始冲击波。随着冲击波在水中的传播，爆炸产物在水中以气泡的形式存在并不断膨胀与压缩，形成气泡脉动现象。

2.1 状态方程

状态方程用来定义固体或流体在各种不同状态下的压力和密度以及比内能之间的函数关系，正确选取状态方程中的参数对于计算结果至关重要。状态方程一般采用半经验半理论的公式，方程中的主要参数由试验确定。

1）TNT爆炸产物状态方程

本文中TNT爆炸产物采用标准JWL状态方程［7］，JWL状态方程是典型的动力学状态方程，它是一种不显含化学反应、由实验方法确定参数的经验状态方程，能比较精确地描述爆轰产物的膨胀驱动做功，其形式为：

式中：p为爆轰产物的压力；η为爆炸气体密度与初始炸药密度的比值，即η＝；A，B，R1，R2和ω为与炸药状态有关的常数；e为TNT单位质量的内能。

2）水的状态方程

在高压、高密度和高温的冲击载荷下，水的状态方程也多种多样，其中最常用的是Mie－Gruneisen状态方程，其具体形式取决于水的状态。在压缩状态下水的压力为：

在膨胀状态下水的压力为：

式中：ρ0为水的初始密度；η＝为水扰动前后的密度比；μ＝η－1，当μ＞0时，水处于压缩状态，当μ＜0时，水处于膨胀状态；C为声速；γ0为Gruneisen系数；a为体积修正系数；S1，S2，S3为拟合系数。

2.2 水下爆炸冲击波的经验计算公式

为了验证数值模拟结果的正确性，采用经验公式进行比较。水下爆炸冲击波的经验计算公式都是建立在爆炸相似律分析和对水下爆炸试验数据进行拟合的基础上的，由于试验数据的不同、拟合方法的不同，经验公式的形式和使用范围也不太一致，其中库尔的经验公式［8］是较为经典的公式，其具体形式如下。冲击波峰值压力经验公式为：

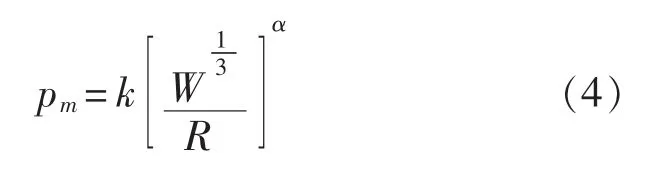
式中：pm为冲击波峰值压力，MPa；W为装药量，kg；R为爆距，m；k为实验系数，取52.4；α为压力衰减系数，对标准TNT炸药，取1.13。

3 SPH数值计算方法

3.1 SPH形式的水下爆炸控制方程

假设爆炸气体和周围水介质是无粘性的，且整个水下爆炸过程被认为是绝热的，因此采用Euler方程作为控制方程。应用SPH核近似和粒子近似可得到以下一系列SPH方程，且在动量方程和能量方程中引入了Monaghan型人工粘性∏ij［9］，它不仅将动能转化为热能，提供了冲击波波面必不可少的耗散，而且防止计算过程中粒子之间的非物理穿透。

Monaghan型人工粘性∏ij表达式为：

光滑长度h在SPH近似方法中非常重要，直接影响到求解的精度和效率。在早期的SPH应用中，光滑长度取决于系统的初始平均密度，而且在整个计算模拟过程中光滑长度保持不变。但是对于水下爆炸问题，由于其为高能高压多介质流动问题，应用常值光滑长度不仅难以对整个物理过程模拟再现，而且爆炸相关局部细节的信息也容易在计算中被遗漏。同时，在水下爆炸的模拟中使用常值光滑长度不仅数值精度难以保证，而且稳定性差，易于造成计算崩溃。因此，必须对光滑长度进行自适应动态变换，本文采用Benz［10］提出的动态自适应方法：

对上式进行SPH近似，可得到以下形式：

下一个时间步长的光滑长度变为：

3.2 固壁边界处理

本文采用固壁粒子配合镜像粒子的方法来模拟固定边界。固壁粒子施加排斥力的方法防止粒子穿越固定边界，排斥力的大小由式（11）确定，固壁粒子参与流体粒子密度及内力的计算，本身的密度不断更新，但位置和速度保持不变。

式中：r0为截止半径，在本文算例中取为初始粒子间距，即1.0／100 m；rij＝ri－rj为粒子i和粒子j的距离；参数n1，n2分别取为6和4；参数D一般取与速度最大值的平方相等的量级，本文取为1.0e6。

图1中粗直线表示刚性壁，圆表示粒子i的支持域。设j位于i的支持域内，若实粒子j关于刚性壁对称的镜像粒子j′也在i的支持域中，则粒子i邻域内的点也包括镜像粒子j′，如果与k对应的镜像粒子k′落在粒子i的支持域外，则计算时不予考虑。由于粒子i也在其支持域内，因此其镜像粒子i′同样需要考虑。

图1 固壁粒子和镜像粒子示意图

3.3 交界面处理

在SPH中，物质交界面处理是一个非常关键的问题，因为SPH方法具有拉格朗日性质和粒子性质，在整个演变过程中，来自不同介质的相互接触的粒子可能会随着运动而分离，甚至有可能不再成为相邻粒子。在水下爆炸模拟中的物质交界面处理更为复杂，因为高压高能的爆炸气体和水之间的激烈相互作用会使粒子的运动相当自由，本文采用的方法是，离得近但材料不同的两粒子可以认为是相邻粒子，这样能够减少在边界附近的粒子缺陷问题，但为了防止粒子的非物理穿透或掺杂问题，在交界面附近的不同粒子之间，当其趋向于穿透时，即：pe＝≥1，施加一个排斥力PBij，其表达式为：

4 水下爆炸过程的数值模拟

4.1 数值模型

在本文算例中，为了简化物理问题，采用了对称的二维水下爆炸模型，即正方形的TNT炸药放置在一个正方形的四周充满水的固壁箱内，固壁边界采用以上处理方法，炸药尺寸为0.1 m×0.1 m，中心坐标为（0 m，0 m），固壁箱尺寸为1 m×1 m，整个离散区域有100×100个粒子，其中100个TNT粒子，9 900个水粒子。初始几何模型如图2所示。炸药从中心引爆后，产生初始冲击波向水中传播，并将能量传入水中，推动水介质向外扩散。TNT药柱初始密度为1 630 kg／m3，其爆轰产物状态方程取为JWL方程，即式（1），式中参数取值见表1；水的密度为1 000 kg／m3，状态方程采用Mie－Gruneisen方程，即式（2）或式（3），式中参数取值见表2。

图2 初始粒子分布图

表1 JWL状态方程中的参数及初始条件

表2 Mie－Gruneisen状态方程中的参数

4.2 数值结果及分析

图3为整个水下爆炸过程中，包括壁面反射之后的粒子速度分布图。从图中可以清楚地观察到向外传播的初始冲击波、从固壁面反射回来的反射波、水的压缩运动以及爆炸气泡的膨胀和压缩等现象。图4为水下爆炸过程中具有代表性瞬间的压力分布，本文采用了Delaunay三角化方法［11］将SPH法求解域中的离散点连接成背景三角形网格，然后用每个背景三角形网格3个顶点物理量的平均值所对应的颜色填充该三角形区域，从而实现无网格法数值结果的云图表征。从图中可以看出，大约200 μs时冲击波到达壁面，然后从壁面反射回来，反射波压缩正在向外膨胀的气泡，大约400 μs时，气泡尺寸达到最大，然后开始被压缩，随着时间的推进，气泡将不断收缩，直至最小，此时气泡完成第一次脉动。这样的向外膨胀和向内收缩会连续出现多次，最终将达到一个平衡状态，但在有限空间中，气泡的脉动周期将会非常短，并不像实际水下爆炸那样会持续几十毫秒，如图5所示，其中气泡半径的大小取为当前时刻爆炸气体粒子区域的等效半径。

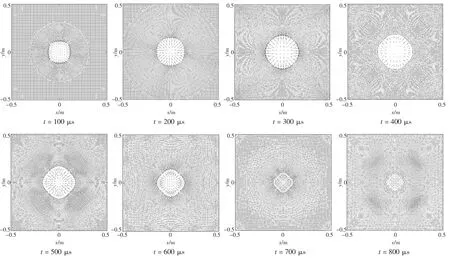
图3 不同时刻的粒子速度分布图

图4 不同时刻的粒子压力分布图

图6给出了在冲击波未到达壁面前，即自由场中，不同爆距处的压力时间历程，从图中可以看出，在峰值压力过后，SPH方法计算的压力值还会有较大的扰动，出现压力的双峰或多峰现象，而经验公式计算的压力则是平滑下降。试验所测得水下爆炸冲击波压力时域曲线一般是不太规则的强间断曲线，且带有多峰现象［12，13］。经验公式中将压力时历曲线作为一个指数衰减函数处理带有一定的近似性。从这一点上来说，SPH数值模拟的这种脉动更符合实际情况。

从图6中还可看出，冲击波压力峰值随距离的增加而减小，这与库尔经验公式是一致的。从表3中数据表明SPH方法计算结果与经验公式（4）计算结果比较吻合，进一步验证了SPH方法用于水下爆炸冲击载荷计算的可行性。

5 结论

本文应用SPH方法成功模拟了整个水下爆炸过程，并给出了不同时刻的粒子速度、压力分布图以及冲击波超压随距离和时间的变化图，所得结果通过与经验公式的比较到达了较高的精度，为舰船水下爆炸冲击载荷的计算提供了一种新型有效的方法。

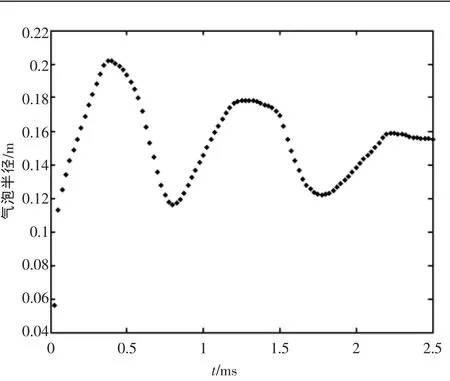
图5 气泡脉动图

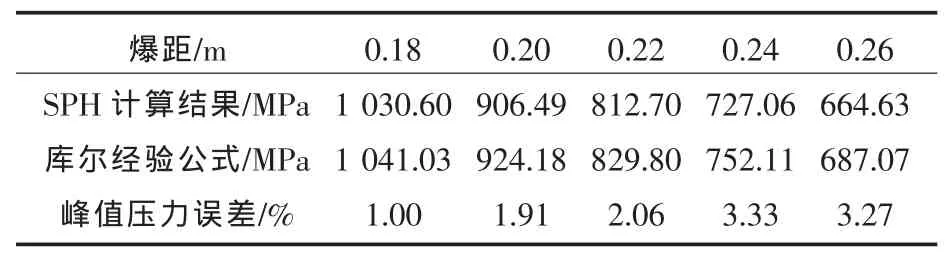
表3 不同距离处冲击波压力峰值计算结果比较

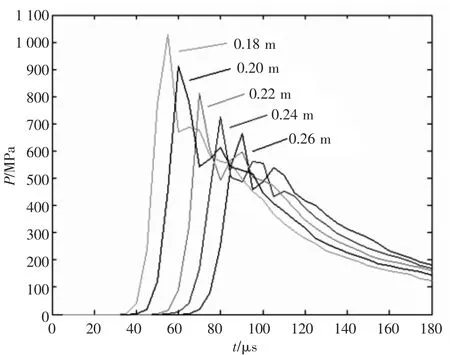
图6 不同距离处的压力时间历程

［1］ COLAGROSSI A，LANDRINI M.Numerical simulation of interfacial flows by smoothed particle hydrodynamics［J］.Journal of Computational Physics，2003，191（2）：448-475.

［2］ 韩旭，杨刚，龙述尧.SPH方法在两相流动问题中的典型应用［J］.湖南大学学报，2007，34（1）：28-32.

［3］ LIU M B，LIU G R，LAM K Y.Smoothed particle hydrodynamics for numerical simulation of underwater explosion［J］.Computational Mechanics，2003，30（2）：106-118.

［4］ LIU M B，LIU G R，LAM K Y.Investigations into water mitigation using a meshless particle method ［J］.Shock Waves，2002，2（3）：181-195.

［5］ 韩旭，杨刚，强洪夫，译.光滑粒子流体动力学——一种无网格粒子法［M］.长沙：湖南大学出版社，2005.

［6］ 张锁春.光滑质点流体动力学（SPH）方法（综述）［J］.计算物理，1996，13（4）：385－397.

［7］ 陈朗，龙新平，冯长根，等.含铝炸药爆轰［M］.北京：国防工业出版社，2004.

［8］ 库尔.水下爆炸［M］.罗耀杰，译.北京：国防工业出版社，1960.

［9］ MONAGHAN J J.Simulating free surface flows with SPH.Journal of Computational Physics，1994，110：399－406

［10］ Benz W.Smoothed particle hydrodynamics：a review，NATO Workshop，Les；Arcs，France.

［11］ 田仲可.无网格法数值结果的云图表征［J］.青岛科技大学学报（自然科学版），2007，28（4）：332－336.

［12］ 池家春，马冰.TNT／RDX（40／60）炸药球水中爆炸波研究［J］.高压物理学报，1999，13（3）：199－204.

［13］ 程素秋，宁永成，张臣，等.相似理论在水下爆炸模型试验中的应用［J］.舰船科学技术，2008，30（3）：95－100.

A New Approach to the Calculation of Impulsive Load of Underwater Explosion

Chen Juan1Xu Yong-qiu2Yao Xiong－liang1Wei Sha1
1 College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China 2 Taizhou Maritime Safety Admimistration People's Republic of China，Taizhou 318000，China

Recently，more and more researches of underwater explosion of warships are focused on the numerical simulations by using computers.Underwater explosion consists of complicated sequence of physical processes，and involves large deformation，large inhomogeneities，moving interfaces and free surfaces.Simulation of underwater explosion problems is a big challenge for the conventional grid－based numerical methods.This paper presents the application of the meshfree smoothed particle hydrodynamics（SPH）method to simulate underwater explosion of warships.And methods are proposed to treat the wall and material interface.Simulation results show the pressure distribution，velocity distribution and the gas bubble evolution and pulsation at representative instants in the underwater explosion process.A new and effective method is provided for research of impulsive load of underwater explosion of warships.

underwater explosion；shock wave；bubble；rigid wall reflection

U661.4

A

1673－3185（2009）03－18－06

2008-12-08

国家自然科学基金资助课题（50779007）；国际科技合作基金资助课题（2007DFR80340）；高等学校博士学科点专项科研基金资助课题（50809018）

陈 娟（1985－），女，硕士研究生。研究方向：船舶与海洋工程结构动力学。E-mail：chenjuan＠hrbeu.edu.cn

许永秋（1966-），男，工程师。研究方向：海事管理

姚熊亮（1963－），男，教授，博士生导师。研究方向：船舶与海洋工程结构动力学，水下冲击载荷作用下结构响应。E-mail：saibei8411@163.com