舰艇作战系统雷达统一对准模型及其误差分析

吕遐东 李 蕾 李维林 马 曦

中国舰船研究设计中心，湖北 武汉430064

舰艇作战系统雷达统一对准模型及其误差分析

吕遐东 李 蕾 李维林 马 曦

中国舰船研究设计中心，湖北 武汉430064

针对舰艇作战系统对准工程的需要，根据坐标变换原理推导了一种统一的舰载雷达探测角度和探测距离的对准计算模型。分析了对准过程中舰艇姿态变化以及仪器测量误差等动态不确定因素对作战系统对准精度的影响，并基于误差理论推导了雷达探测角度和探测距离对准理论真值的最大绝对误差计算公式。根据上述模型计算舰载雷达对准的理论真值及其最大绝对误差，可以为舰艇作战系统对准精度分析提供辅助依据。Matlab数值仿真结果验证了本文方法的有效性。

舰载作战系统；坐标变换；雷达对准模型；误差分析

1 引言

舰艇作战系统对准是确保战斗舰艇充分发挥作战效能、保证武器命中概率的关键性工作［1］。参照我国国军标对“系统对准”的定义，舰艇作战系统对准是将全舰探测器、跟踪器、武器系统、导航等系统（设备）的机械零位与电气零位在甲板坐标系内取齐，即把机械零位和电气零位统一于一个基准，以保证作战系统零位的一致性［2－5］。

雷达探测角度和距离对准是舰艇作战系统对准的一项主要内容［6－8］。考虑舰艇系泊或者海上锚泊的动态环境，本文推导了一种统一的舰艇雷达探测角度和距离的对准计算模型，分析了舰艇姿态变化以及对准测量误差对作战系统对准精度的影响，并结合上述模型给出了对准约定真值最大绝对误差计算公式。仿真计算结果验证了本文方法的有效性。

2 舰艇作战系统对准坐标系

如图1所示，N1、N2为定义的大地正北方向。M为架设的孤立雷达反射体，M′为M在大地水平面的投影点；A为人为选取的岸基点，雷达反射体相对于岸基点的大地测量结果已知，即距离r1＝｜AM｜、方位角α1＝∠M′AN1和仰角β1＝∠M′AM已知；AP为岸基线，岸基线的方位角∠PAN1可以通过GPS测量得到。

PQ代表舰艇中心艏艉线，考虑舰艇探测设备非对称分布的布置情况，B为在舰甲板面上选取的任一舰基点，B′为B在水平面的投影点，在A点架设全站仪，B点放置反射棱镜，距离l0＝｜AB｜、仰角β0＝∠B′AB和角度∠B′AP可实时测得。定义角度变量ω＝∠B′AN1＝∠B′AP－∠PAN1，ω可由全站仪测量量∠B′AP和GPS测量量∠PAN1计算得到。

C为某雷达回转面的中心点，C′为点C在甲板面的投影点。在图1、图2中，l1为B、C两点在甲板面艏艉线垂直方向的间距，l2为两点在艏艉线方向的间距，l3＝｜CC′｜为两点在垂直甲板面方向的间距，假设l1、l2和l3为已知参数。

图1 舰艇作战系统对准坐标系－1

图2 舰艇作战系统对准坐标系－2

O点为舰主基准面的中心点，Y0轴正方向为舰首方向，X0OY0为舰主基准面，建立舰主基准坐标系Ω0：OX0Y0Z0；以A为原点，正北方向N1为Y1轴正方向，垂直水平面向上为Z1轴正方向，建立岸基点坐标系Ω1：AX1Y1Z1；以B为原点，正北方向N2为Y2轴正方向，垂直水平面向上为Z2轴正方向，建立舰基点坐标系Ω2：BX2Y2Z2；以C为原点，Y3轴正方向为舰首方向，X3CY3为探测器回转面，建立雷达坐标系Ω3：CX3Y3Z3。

3 舰艇雷达统一对准模型

假设雷达反射体M在岸基点坐标系Ω1中的坐标为P1＝［x1y1z1］T，P1和参数r1、α1和β1存在下述关系：

点M在舰基点坐标系Ω2中的坐标为P2＝［x2y2z2］T。欧氏空间中坐标系Ω1和Ω2间的变换关系可分解为旋转变换矩阵R和平移向量T：

结合图1和图2中舰艇对准坐标系中的几何关系推导可知：旋转矩阵R＝I，平移向量T＝［l0cos β0sinω－l0cos β0cosω－l0sin β0］T，将其代入式（2）得：

在系泊或者海上锚泊等动态环境下测得舰艇实时姿态信息：纵摇角φ（艏高为正）、横摇角θ（左舷高为正）和艏向角ψ（顺时针旋转为正），约定从舰艇坐标系到岸基点坐标系的旋转变化顺序为先ψ再φ最后θ。

如图3所示，相对于舰主基准坐标系Ω0：OX0Y0Z0，纵摇旋转变换矩阵R1（φ，X0）、横摇旋转变换矩阵R2（θ，Y0）和艏向角旋转变换矩阵R3（ψ，Z0）分别为［9］：

图3 舰艇姿态变化方向

且上述变换矩阵还存在下述关系：

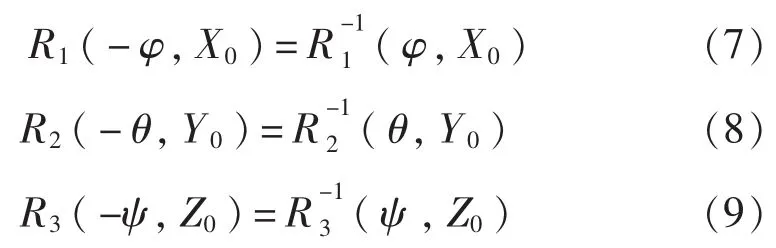
定义雷达反射体M在雷达坐标系Ω3：CX3Y3Z3中的位置坐标P3＝［x3y3z3］T。舰载雷达探测器通常可分为两类：搜索雷达和跟踪雷达。搜索雷达平面X3CY3与大地水平面平行，跟踪雷达平面X3CY3与舰主基准面X0OY0平行（理想情况，忽略船体变形等因素）。我们对其分别进行讨论。

1）根据坐标系旋转和平移变换原理，搜索雷达坐标系Ω3中的位置坐标P3和舰基点坐标系Ω2中的位置坐标P2之间存在下述关系：

联立式（3）和式（10）可得：

2）同理，跟踪雷达坐标系Ω3中的位置坐标P3和舰基点坐标系Ω2中的位置坐标P2之间的转换关系如下。

联立式（3）和式（12）可得：

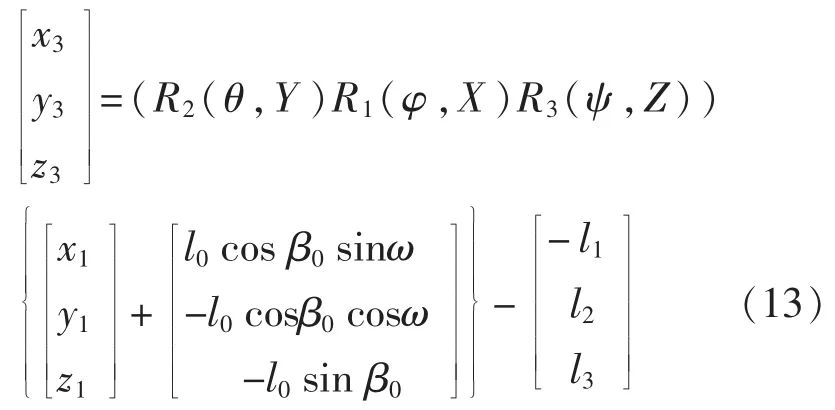
式中参数k的具体数值要结合位置坐标x3和y3的正负号决定。

若已知雷达反射体M相对于岸基点A的大地测量真值：方位角α1、仰角β1和距离r1，以及全站仪和GPS的测量结果l0、β0、ω，综合式 （1）、式（11）或式（13）、式（14），可求得标定物M在雷达坐标系Ω3中的方位角、仰角和距离，并将其作为舰载雷达探测角度和距离对准时的约定真值。

4 舰艇雷达对准模型误差分析

在舰艇海上系泊等动态环境下进行雷达探测角度和距离标校时，由于全站仪和GPS测量、对准约定真值计算以及雷达探测读数三者之间无法在时间上保持同步，舰艇姿态的动态变化会导致雷达对准约定真值计算误差，同时全站仪和GPS的测量偏差也会给对准真值的计算带来影响。因此有必要综合舰艇姿态变化以及对准测量偏差等动态不确定因素分析其对作战系统对准精度的影响。

根据式（11）或式（13）可知雷达反射体在舰艇雷达坐标系Ω3中的位置坐标变量x3，y3，z3与舰艇姿态φ、θ、ψ和GPS、全站仪测量ω、l0有关，即x3＝x3（φ，θ，ψ，ω，l0）、y3＝y3（φ，θ，ψ，ω，l0）和z3＝z3（φ，θ，ψ，ω，l0）。根据误差传递理论，坐标值x3，y3，z3的最大绝对误差Δx3、Δy3、Δz3可由式（15）计算。

式（15）中∂i/∂j（i＝x，y，z），（j＝φ，θ，ψ，ω，l0）为变量i关于j的偏微分，Δφ，Δθ，Δψ为舰艇姿态在初始值φ0，θ0，ψ0附近的最大绝对变化量；Δω、Δl0为全站仪和GPS的最大绝对测量误差。

联立式（15）和式（16），可求得雷达探测方位角、仰角和距离对准约定真值的最大绝对误差Δ、Δ、Δ。反之，根据雷达对准约定真值的精度要求，我们可以判定在动态条件下满足作战系统对准要求的舰艇姿态以及全站仪、GPS误差变化范围。

5 仿真计算

在系泊状态下，假设舰艇姿态角A的摇摆变化用下述模型简化描述［10］：

式中，Am为摇摆幅值；a为初始相位角；T为摇摆周期，对于大型水面舰艇，横摇周期约为8～12 s，纵摇周期约为 4～5 s。

假设被标定雷达类型为搜索雷达，有关参数假定如下：雷达发射体M同岸基点A的距离r1＝10 000 m，仰角β1＝0.6°，方位角α1＝40°；舰基点B同岸基点A的距离l0＝40 m，仰角β0＝15°，ω＝70°；雷达回转面中心M同舰基点的距离变量l1＝20 m，l2＝100 m，l3＝25 m；假设舰艇姿态初始值θ0＝0，φ0＝0，ψ0＝10°；横摇角绝对变化量为Δ θ＝｜3sin（πt／6）｜，其中横摇幅值3°，横摇周期12 s，初始相位角为0；纵摇角绝对变化量为Δ φ＝｜sin（2πt／5＋π／3）｜，其中艏摇幅值1°，艏摇周期5 s，初始相位角π／3；艏摇绝对变化量Δ ψ＝0；假设全站仪和GPS的最大测量误差为Δ ω＝10″，Δ l0＝15 mm。

根据上述推导的舰艇雷达统一对准模型和约定真值误差计算公式，利用Matlab7.0科学计算软件进行仿真计算，计算步长取0.1 s。计算结果为：雷达探测角度和距离对准的约定真值＝50.727°，≌0.42°，＝9 965 m。

考虑舰艇姿态实时变化以及全站仪和GPS的测量误差等对准不确定性因素，上述约定真值的最大绝对误差变化曲线如图4～图6所示：

图4 雷达对准方位角约定真值最大绝对误差

图5 雷达对准仰角约定真值最大绝对误差

图6 雷达对准距离约定真值最大绝对误差

由图4～图6可知，在0～60 s的时间段内搜索雷达针对雷达发射体M的对准约定真值最大绝对误差变量 Δ、Δ、Δ的最大值分别为 0.005 86°、0.014 1°和1.094 m。

6 结论

雷达探测角度和距离对准是舰艇作战系统对准的一项主要内容。本文推导了一种统一的舰艇雷达探测角度和距离对准的计算模型，分析了舰艇姿态变化以及对准测量误差等动态不确定性因素对于作战系统对准理论真值误差的影响，并结合对准模型给出了对准约定真值最大绝对误差计算公式。根据上述模型完成对准理论真值和真值最大绝对误差计算，可为舰艇作战系统对准精度分析提供辅助依据。

［1］李蕾，唐伟方.作战系统对准软件的开发与研究［J］.舰船电子工程，2002（4）：18－20.

［2］马恒，许江宁，朱涛.高精度舰艇航向姿态信息标校方法和测量模型研究 ［J］.中国惯性技术学报，2004，12（2）：77－80.

［3］邹立.动态条件下导航系统航向对准 ［J］.舰船光学，2003，39（3）：30－34.

［4］欧阳寰，刘忠.基于图像处理技术的舰载武器系统对准方法［J］.海军工程大学学报，2003，15（2）：81－84.

［5］姚景顺，杨世兴.舰载雷达的动态标校［J］.火力与指挥控制，2008，33（3）：128－130，134.

［6］刘高峰，刘健.基于GPS定位系统的舰船雷达标校系统研究［J］.舰船科学技术，2006，28（6）：100－102，114.

［7］刘勇，叶显武，李兴民.舰载雷达CCD激光经纬仪标校方法研究［J］.现代雷达，2007，29（11）：13－16.

［8］朱起悦.应用差分GPS技术进行雷达标校［J］.电讯技术，2006，46（1）：108－110.

［9］李殿璞.船舶运动与建模［M］.北京：国防工业出版社，2008.

［10］邵开文，马运义.舰船技术与设计概论［M］.北京：国防工业出版社，2005.

A Unified Radar Alignment Model with Error Analysis for Shipboard Combat System

Lü Xia－dong Li Lei Li Wei－lin Ma Xi
China Ship Development and Design Center，Wuhan 430064，China

Based on coordinate transformation theory，a unified computation model was proposed for shipboard radar＇s alignment of detection angle and distance.The model well meeted the requirements for the calibration engineering of shipboard combat system.The influences of ship attitude variation and instrument measure errors on combat system＇s theoretical calibration values were analyzed.On the basis of the error theory，the model also developed a set of equations to determine the maximum absolute errors of theoretical alignment values of the radar.With the above alignment computation，the model is can assist the calibration in the precision analysis of shipboard combat system.Matlab data simulation results demonstrate the calibration model＇s effectiveness.

shipboard combat system；coordinate transformation；radar alignment model；error analysis

U665.22

A

1673－3185（2009）06－53－05

2008－09－22

海军“十一五”装备预先研究项目

吕遐东（1977－），男，博士，工程师。研究方向：舰船电子信息系统。E鄄mail：xd_lv＠163.com