层次分析法在潜艇总体性能评估中的应用与改进

孙海涛 熊 鹰 谢海燕 张永坤

海军工程大学 船舶与动力学院，湖北武汉430033

层次分析法在潜艇总体性能评估中的应用与改进

孙海涛 熊 鹰 谢海燕 张永坤

海军工程大学 船舶与动力学院，湖北武汉430033

结合潜艇概念设计阶段的特点，提出一种潜艇总体性能的评估模型和评价方法，利用三标度法间接给出判断矩阵，在一定程度上减少了决策者主观因素的影响。针对经验方法在一致性检验时的缺陷，采用统计检验的方法，直接以判断矩阵一致性指标的临界值作为检验标准，简洁可行，且具有一定的理论依据。

潜艇总体性能；性能评估；层次分析法；判断矩阵

1 引言

在概念设计阶段，潜艇总体性能的评价对于评估设计方案的优劣，进行方案优选是至关重要的。由于舰船设计的复杂性和系统性，依靠主观想象和经验的传统评估方法急需改进，促使设计者寻找新的方式。

层次分析法（AHP）将决策者的定性分析和定量判断结合起来，以其实用、简洁等优点受到广泛重视，迅速得到应用。DEMKO［1］、曾广会［2］等人将该方法应用于船舶的设计评估，尹曰建［3］、周勇［4］等人探讨了其在作战能力评估中的应用。但上述文献中，使用传统的九标度法构建判断矩阵，采用经验方法进行一致性检验，均有需要完善的地方。本文采用改进后的层次分析法，建立了潜艇总体性能层次结构模型，利用不同于以往的判断矩阵构造法和一致性检验法，并结合实例提出一种性能评估的方法。

2 层次分析法原理

层次分析法是美国运筹学家于20世纪70年代初提出的，它使决策者形象化地使用属性层次结构来构造复杂的多属性决策问题。从本质上讲，层次分析法是人类对复杂问题层次结构理解的形式化。运用层次分析法方法进行决策时，大体上可分为以下4个步骤［5］：

1）分析系统中各因素之间的关系，建立系统的递阶层次结构；

2）对同一层次的各元素关于上一层次中的某一准则的重要性进行两两比较，构造两两比较判断矩阵；

3）由判断矩阵计算被比较元素对于该准则的相对权重；

4）计算各层元素对系统总目标的组合权重。

2.1 建立递阶模型

将AHP应用于复杂的决策问题，首先要分析问题的结构，构造出一个层次分析的结构模型，决策问题分解为被称作“元素”的组成部分，如准则、属性、约束、方案等。然后按其属性把这些元素分组形成互不相交的层次，上一层次对下一层次的全部或部分元素起支配作用，这样就形成了层次间自上而下的逐层支配关系，即递阶层次关系。通过对决策问题做充分的了解和详尽的分析，建立一个有效的合理的递阶层次结构，对于成功解决问题具有决定性意义。

2.2 构造判断矩阵

建立递阶层次模型以后，上下层次之间元素的隶属关系就此确定。假定以顶层元素x0为准则，其所支配的下一层次的元素为x1，x2，…，xn，通过两两相互比较的方法求出它们对于准则x0的相对重要性，这样下层n个被比较元素就构成一个两两比较判断矩阵：

式中，aij表示元素xi与xj相对于x0的重要性的量化值。

显然判断矩阵具有下述性质：∀i，j∈N，有

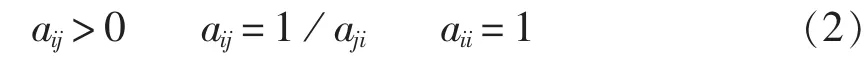
因此，称判断矩阵A为正互反矩阵。

传统的判断评价方法采用九标度法，含义如表1所示。这种标度法的定义本身具有科学性和合理性，但在实际操作过程中，决策者难以使用从一到九标度准确表示各元素的相对重要性程度，容易产生矛盾和混乱，从而导致判断上的偏差。

表1 AHP标度值含义

针对上述问题，本文采用三标度法构建两两比较矩阵［6］，再利用数学关系式将比较结果转换成相应的九标度值，间接给出判断矩阵。

首先用三标度（0，1，2）构造两两比较判断矩阵：

其中，cij＝2，表示第i个元素比第j个元素重要；cij＝1，表示第i个元素与第j个元素同样重要；cij＝0，表示第i个元素没有第j个元素重要。

然后逐行相加得排序指数：

判断极大、极小排序指数对应两元素的相对重要程度bm，设rmax表示最大排序指数，rmin表示最小排序指数，其对应基点元素分别为xmax和xmin，则bm为xmax对xmin的重要性程度量化值，称为“基点标度”，做如下变换：

变换式（3），根据基点标度bm，将各元素的排序指数之差从［0，（rmax－rmin）］区间变换到能反应元素相对重要程度的［1／bm～bm］区间。

使用三标度法，仅需要判断两元素之间的重要关系而无需给出重要性程度值，操作方便，具有较好的一致性。决策者只要给出合适的bm值，就可得到合理的判断矩阵。

2.3 计算元素相对权重

根据判断矩阵A＝（aij）n×n计算此 n个元素对于准则x0的相对权重向量ω＝（ω1，ω2，…，ωn）T，并进行一致性检验。

2.3.1 权重计算方法

权重的计算方法主要有算术平均法、几何平均法、特征根法、最小二乘法、对数最小二乘法、最小偏差法、梯度特征向量法、广义特征根法等。其中，特征根法被较早提出并得到广泛应用，对层次分析法的发展发挥了重要作用。特征根法也称“特征向量法”，首先求解判断矩阵的最大特征根。

式中，λmax为A的最大特征根；ω是相应的特征向量。所得ω经归一化后即可作为权重向量。

2.3.2 一致性检验

在构建判断矩阵时，由于客观事物的复杂性和主观认知的局限性，判断经常伴有误差，判断矩阵一般不可能具有完全一致性，因此进行一致性检验是必要的。

一致性检验的通用方法是按式（5）计算一致性比例C.R.，当C.R.＜0.1时，认为判断矩阵的一致性是可以接受的。

C.I.为一致性指标，按下式计算：

R.I.为平均随机一致性指标，是C.I.的抽样平均值。

尽管上述检验方法操作方便，也已被多数层次分析法使用者所接受，但也存在一定的缺陷。数据0.1是美国运筹学家Saaty根据经验推荐的一致性比例C.R.的临界值，其选取缺乏必要的理论依据。另外在应用上，采用0.1作为临界值进行检验时，低阶矩阵容易通过，而7，8阶或更高阶矩阵则难以满足其要求。从模拟试验得出的图1可以看出，随着矩阵阶数的增加，R.I.的值增大且趋于一个稳定值，同时最大、最小C.I.的样本值也随之增加而趋于R.I.值。中高阶矩阵的最小值明显较大，这表明采用0.1作为临界值对低阶矩阵要求过松，而对于高阶矩阵又过于苛刻。

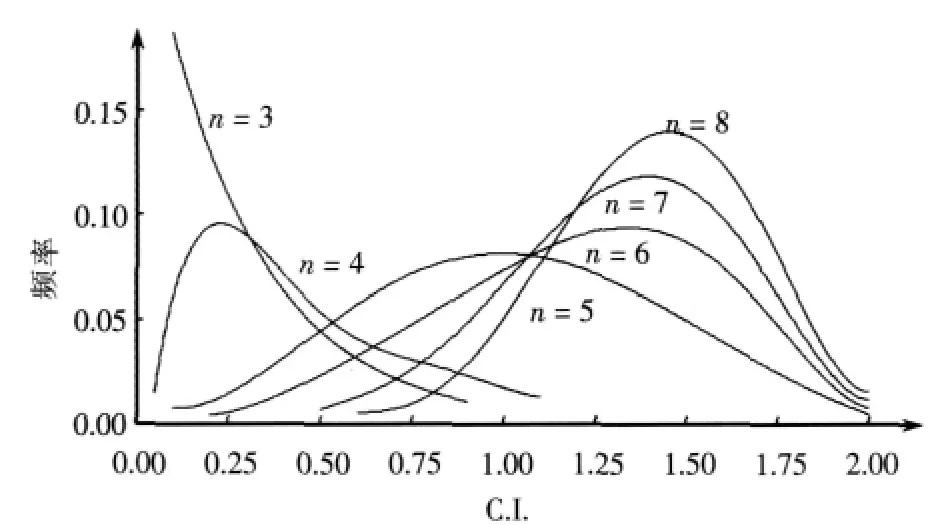
图1 不同阶数随机正互反矩阵一致性指标分布

鉴于此，本文采用统计检验的方法，直接寻求各阶矩阵的临界C.I.值，将其作为一致性检验的标准。假设δij为判断矩阵的元素对于某个一致性矩阵对应元素的相对扰动量，由于人的比较判断在直觉上具有一致性趋势，因此δij总是在0附近取值。假定δij在（－1，1）上服从正态分布，则n（n－1）／μ近似服从χ2分布［7］。为得到所需临界值，需对δij的分布做更强的假设。由于其相对集中于0附近，有学者推荐方差σ2＝1／2，因此可进一步假定δij～N（0，1／2），一致性检验可归结为检验假设：

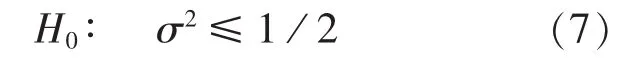
统计量

的自由度为n（n－1）／2，此时σ02＝1／2。在一定的置信水平（1－α）上，通过查χ2表可得到n阶矩阵χ2的临界值λα（右单边检验），那么μ的临界值μ0应为：

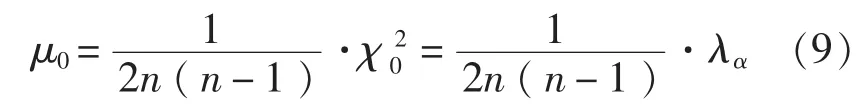
表2列出了置信水平为90%的μ临界值。当判断矩阵的C.I.的计算值小于表中相应临界值时，认为该判断矩阵具有满意的一致性。值得说明的是，1阶和2阶判断矩阵总是完全一致的。

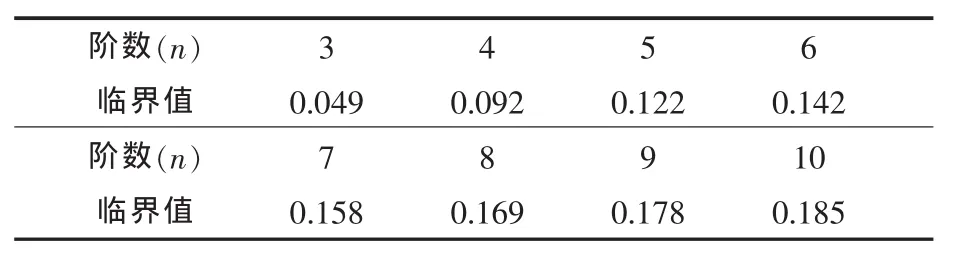
表2 统计检验法一致性指标的临界值

为便于比较，将相应的用经验方法控制C.R.＜0.1时C.I.的临界值列出，如表3所示［8］。对比发现，对于阶数较大的矩阵，统计检验法的临界值明显较大，修正了经验方法对高阶矩阵要求苛刻的现象。另外，统计检验法采用检验统计量是C.I.，计算上更为简便，并且具有一定的理论依据。

表3 经验方法一致性指标的临界值

2.4 计算各层组合权重

欲进行决策和评估，最终需要各层元素对总准则的相对权重，这就要自上而下地将单层元素权重进行合成，取得最底层相对于最高层的合成权重。

设已求出第k－1层元素的权重向量ω（k－1）＝T，nk－1为k－1层元素个数。若第k层上nk个元素对第k－1层上第j个元素为准则的单权重向量设为，其中不受j支配的元素的权重取值为0。P（k）＝（P1（k），P2（k），…，Pnk－1（k））nk×nk－1，表示k层上nk个元素对k－1层上各元素的合成权重，那么k层元素对顶层总准则的合成权重向量ω（k）由下式给出：

由此递推得：

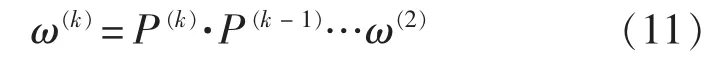
式中，P（k－1）为第k－1层对上一层各元素的权重构成的nk－1×nk－2矩阵，ω（2）为第2层元素对总准则的单权重向量。

同样地，一致性检验也需要从上到下逐层进行。若已知以k－1层上元素为准则的一致性指标为C.I.j（k），那么k层的综合一致性指标C.I.（k）应为：

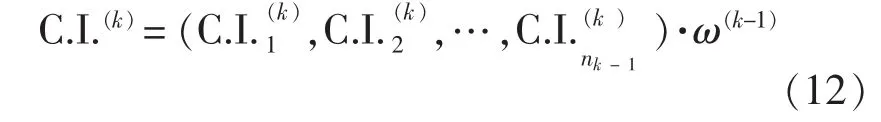
3 潜艇总体性能评估

3.1 潜艇总体性能层次模型

将潜艇总体性能作为最高准则，建立概念设计阶段的层次结构模型，如图2所示。更为详尽的层次结构，可以在后续的开发和设计中进一步讨论。

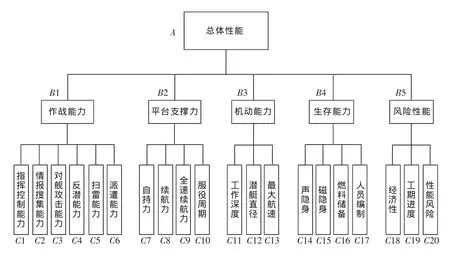
图2 层次结构图

3.2 性能评估

3.2.1 构建判断矩阵和计算权重

以作战能力为例，建立其两两比较判断矩阵B1′：

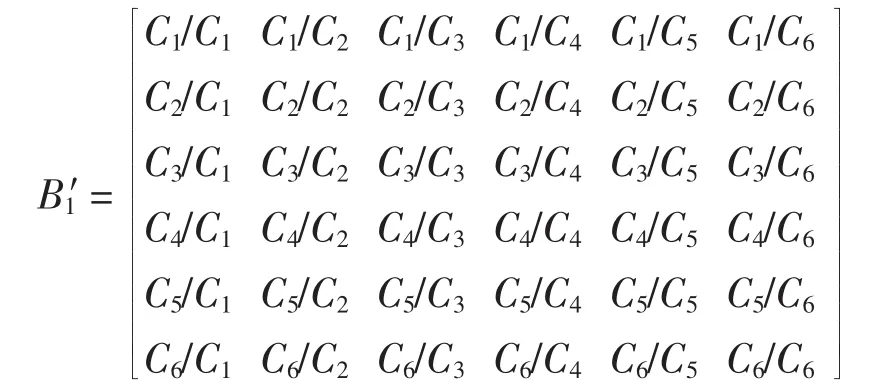
根据该型潜艇的作战任务要求，指挥控制、情报搜集和派遣能力较其他元素重要，三标度判断矩阵如下：

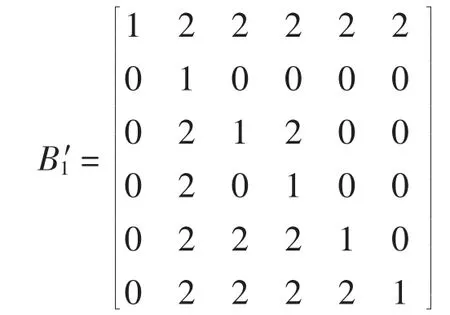
此时，rmax=11，rmin＝1，令 bm＝6，对应的九标度判断矩阵为：

最大特征根λmax＝6.122 5，将对应特征向量进行归一化得到元素C1～C6相对于该准则的单权重向量为（0.382 5 0.042 8 0.100 6 0.064 1 0.159 6 0.250 4）T。一致性指标C.I.＝0.024 5，远小于表2中相应的临界值，满足一致性要求。

对各准则进行判断，并进行一致性检验，最终通过组合计算得到底层各元素相对于总准则的权重向量为 （0.160 1 0.017 9 0.042 1 0.026 8 0.066 8 0.104 8 0.050 2 0.018 4 0.010 2 0.018 4 0.039 3 0.016 0 0.006 5 0.072 8 0.042 0 0.122 7 0.025 0 0.026 1 0.047 5 0.086 3）T。总的一致性指标为0.016 9，比表2中任何一个临界值都小，足以满足一致性要求。

3.2.2 综合评价

底层各指标的权重ωi确定后，可结合其性能值利用效用函数进行综合评价，公式如下：

式中，qi为单个指标的性能值。各元素性能值可采用多属性效用理论计算得出［9］，将所求数值代入上式可得到潜艇总体性能指数的值。

4 结论

1）在研究潜艇概念设计特点的基础上，本文建立了总体性能评估结构模型。针对九标度法构建判断矩阵时的缺陷，采用客观性较强的三标度法构建判断矩阵，减少了决策者主观因素的影响，具有较好的一致性。

2）利用统计检验方法对判断矩阵进行一致性检验，具有一定的理论依据，并且改善了经验方法对高阶矩阵要求苛刻的现象。

3）在底层元素相对于总准则的合成权重已经确定的情况下，本文最后结合多属性效用理论给出潜艇总体性能指数的计算公式。

通过典型案例验证，本文的评估方法取得了较好的效果，可用于概念设计阶段潜艇总体性能的评估或多个概念方案的决策优选，有助于提高潜艇设计效率与水平。

［1］DEMKO D T.Tools for Multi－objective and Multi－disci鄄plinary optimization in naval ship design［M］.American：Viginia Polytechnic Institute and State University，2005.

［2］曾广会，朱军，胡忠平.基于AHP与MAUT的舰船概念设计评估方法研究［J］.造船技术，2007（4）：8－12.

［3］尹曰建，浦金云.现代作战舰艇生命力的层次分析法综合评估［J］.长春工业大学学报（自然科学版），2004，25（3）：36－38.

［4］周勇.层次分析法在潜艇作战能力评估中的应用［J］.情报指挥控制系统与仿真技术，2004（3）：42－45.

［5］徐玖平，吴巍.多属性决策的理论与方法［M］.北京：清华大学出版社，2006.

［6］左军.层次分析法中判断矩阵的间接给出法［J］.系统工程，1988，6（6）：56－63.

［7］王莲芬，许树柏.层次分析法引论［M］.北京：中国人民大学出版社，1990.

［8］SAATY T L.The analytic hierarchy process［M］.New York：McGraw－Hill，1980.

［9］BROWN A J，THOMAS M.Reengineering the naval ship concept design process［C］//Research to Reality in Ship System Engineering Symposium，ASNE，September，1998.

Analytic Hierarchy Process in the Assessment of Submarine Overall Performance

Sun Hai－tao Xiong Ying Xie Hai－yan Zhang Yong－kun
College of Naval Architecture and Power，Naval Univ of Engineering，Wuhan 430033，China

Considering the characteristics of submarine concept design，a new evaluation model and measure was put forward to assess the overall performance of submarine.By using a three level domi鄄nance scale method，the comparison matrix was created indirectly，which reduced the influence of deci鄄sion maker＇s subjective experience to a certain extent.The statistical method，which takes the critical value of consistency index（C.I.）of the comparison matrix as the test criterion，was used to test the con鄄sistency of the pair－wise judgments.This method is simple，practical，and theoretically feasible.

submarine overall performance；performance evaluation；Analytic Hierarchy Process（AHP）；comparison matrix

U674.76

A

1673－3185（2009）06－38－04

2008-12-15

孙海涛（1985－），男，硕士研究生。研究方向：船舶流体力学。E鄄mail：sunhaitao2004328＠yahoo.cn

熊 鹰（1958-），男，教授，博士生导师。研究方向：船舶流体力学。E鄄mail：xiongying0920＠163.com