次贷危机与金融衍生产品定价失当

杨晓光， 唐 跃， 陈 浩

(1. 长沙理工大学 金融工程与金融管理研究中心，湖南 长沙 410076；2. 中国科学院 数学与系统科学研究院，北京 100190)

一、引言

肇始于美国的次贷危机很快演变成一场波及全球的金融危机，并且对世界经济造成巨大的冲击。在这场危机中扮演主要角色的是次级贷款以及基于次级贷款的金融衍生产品，而这些产品得以能够有市场有交易，关键就是能够对它们进行定价，而金融衍生产品的定价，离不开相对而言高深复杂的金融数学。

次级贷款又名次级抵押贷款和次级按揭贷款。正常情况下，客户向银行或其他贷款机构申请贷款，定期偿付本金和利息，形成贷款合约。但一部分客户由于信用条件或其他原因未能满足正常贷款发放的要求，贷款机构无法与他们签署直接贷款协议，为了满足这部分客户的要求，贷款机构发放了对客户信用要求宽松但贷款利率更高的贷款，这就是次级贷款。具体而言，次级贷款即为发放给信用评分在500～620贷款人的住房抵押贷款。次级贷款的特点：发放贷款时不考虑借贷人的财务状况；首付很低或者没有首付；初始还贷利率很低；蕴涵着巨大的违约风险，历史违约率远远大于优先级和Alt-A级贷款。以前次级贷款人是不能获得信用贷款的。2001年以后，美国房价上涨速度加快，形成房价持续上涨预期，各类房地产金融机构为了获取更高利润，在满足优质客户的信贷需求以后，开发面向次级贷款人、利率水平相对较高的次级贷款。从2001～2006年，美国抵押贷款增长30%，次贷增长200%。

根据Inside Mortgage Finance2007年报告显示，2001年到2006年间，次级贷款占按揭贷款的比重直线上升，由2001年的9%上升到2006年的23.8%。次贷风险得以放大并贯穿整个金融系统的载体是基于次贷的衍生产品，这些衍生产品的高收益是促进次贷膨胀的主要原因之一。据IMF统计显示，从2001年到2005年，全球信用衍生品市场呈现爆发式增长，截至2005年，全球信用衍生品市场规模达到17万亿美元，2006年这一数字达到35万亿美元，与全球GDP总额大致相当。

在这些衍生品繁荣的过程中，金融数学是衍生品发展的理论基础。衍生品的交易需要有价格作为交易的基础，与普通商品不同，衍生品看不见摸不到的特性使得衍生品的价格确定无法通过人为简单判断估计确定。在20世纪，随着金融数学作为一个独立的学科分支出现，特别是BS期权定价公式出现后，金融家们发现金融数学模型可以为衍生品的定价工作提供支持，实践效果也可以接受。随着金融衍生品的发展和繁荣，衍生品的结构越来越复杂，金融数学的工具也应用得越来越广泛。2006年以前，利用金融数学模型为衍生品定价的方法已经被普遍采用，金融数学专家也被业界和学术界视为天之娇子。但是由于衍生品的大量使用是这次次贷危机主要原因之一，次贷危机发生后，社会上有一种观点认为，复杂的金融数学模型是华尔街金融大鳄们忽悠民众、贪婪掘金的“帮凶”。本文在简述次贷衍生产品在危机中的作用之后，对次贷衍生产品的基本定价模型进行考察，分析这些模型运用失当之处，并讨论如何正确认识金融数学的作用。

二、衍生产品在次贷危机中的作用

这次次贷危机影响范围广，传导链条长，具体过程大致概括如下。首先，购房者与放贷机构签订贷款合同，放贷机构为购房者提供住房贷款，购房者按期偿还贷款。这种类型的贷款相当于放贷机构持有了购房者的债权，而这种债权有购房者停止偿还贷款的信用风险，所以放贷机构不愿单独承担此类风险而希望把风险转移出去。于是放贷机构与房利美，房地美和抵押贷款公司或银行达成协议，放贷机构将购房者的贷款出售给上述机构。类似的，上述机构也不愿意独自承担所有风险，于是购房者的贷款又以MBS的形式打包出售给投资银行，投资银行再将这些产品进一步采用CDO打包出售给保险机构和对冲基金等投资者。最后投资者之间会签订CDS等协议进行风险转移。在这个金融创新链条上，牵涉到了商业银行、抵押贷款公司、投资银行、保险机构、对冲基金等金融机构，所以在这次次贷危机中，上述金融机构都受到了不同程度的影响。

具体而言，这次次贷危机涉及的衍生产品主要有MBS、CDO、CDS三类。MBS(抵押贷款支持证券，即Mortgage backed security)：是将若干抵押贷款组成资产池,在其还本付息所产生的现金流基础上发行的证券。MBS的金融原理第一是“打包”；第二是“分级”，即排定一个优先偿付顺序；第三是“升级”，通过保险公司提供保险等多种手段，实现信用升级。

CDO(抵押债务债券，即Collateralized Debt Obligation)，是将若干固定收益资产(MBS)再次打包，重新分配现金流偿付的优先次序，再划分出高层、夹层、权益层等不同层次的债券。CDO的发行人(通常是投资银行)经过优先偿付分级、信用升级等手段，保证高层债券从评级公司获得AAA/Aaa评级。危机前的CDO呈现出两个特点：一是高风险的次级抵押贷款经过层层包装后，大部分进入CDO的高层和夹层，打上了投资级甚至AAA/Aaa评级的标签；二是CDO的年回报率大致为300%，高于同等评级的传统证券，出现了“同风险，不同收益”怪现象。马克思有句名言，“有300%的利润，资本就敢犯任何罪行，甚至冒绞首的危险”。CDO的高回报率，使得投资机构对CDO产品趋之若鹜，进而创造出CDO2、CDO3乃至CDOn等更多名目的衍生品种,并进一步推动了对次级抵押贷款及其证券化产品的需求。

CDS(信用违约掉期，即Credit Default Swap)：信用违约掉期不局限于对一个实际的违约事件进行补偿，它在交易条款中包含信用等级降低这样的事件。在一个违约掉期交易中，风险保护的卖方将获得买方提前支付或分期支付的一定费用作为回报，当信用资产的所有者违约或信用级别降低时，补偿买方因此而承受的损失。在市场处于上升期的阶段里，CDS的卖方坐收无成本的现金流收益，而CDS买方信用产品的信用等级得到很大的提高，使得这些原本风险很大的产品进入投资级。在次贷危机之前，由于美国房地产市场的一路上扬，CDS买卖双方都从中获利，CDS得到蓬勃发展，全球CDS存量从2004年的6万4千亿美元，激增到2007年57万9千亿美元。CDS的激增也推动了次级贷款、MBS、CDO的大幅增加。

三、次贷衍生产品定价模型与运用失当

目前，信用衍生产品定价主要分为两大类，结构性模型(Structural Model)和简约模型(Reduced-Form Model)。结构性模型由Merton首先提出。模型主要假设为公司资产服从对数正态分布，当公司资产低于某门槛时，即发生违约，结构模型从描述信用产品发行人本身的资本结构入手，假定违约事件是由公司内部因素造成的。简约模型是由Jarrow等人所提出，其主要模型假设为违约是随机发生的，且服从随机跳跃过程。简约模型着眼于违约或信用评级变动等事件发生的概率，并将它与市场可观测的信用利差联系起来，而不深究造成违约的原因。目前，多个资产间的违约相关性模型几乎都是建立在这两个模型之上，当前国际上流行的CDO定价方法主要是建立在简约模型的基础之上。

CDO的构造是相当复杂的，要准确理解CDO并不容易，而要对不同等级的CDO证券进行评级和定价自然就更加困难了。

CDS是部分融资合成型CDO得以构建的基础，而CDO证券的持有者能否按期收回本金与利息，首先也取决于CDS是否违约。在次贷危机爆发后，由于很多次级抵押贷款债权(参照实体)出现违约，很多超优先级投资者因为支付不起巨额的CDS赔偿金而濒临破产，由于不能收到超优先级投资者的赔付，发起人也不再向SPV 支付CDS保费，这就导致CDO证券出现违约，最终造成持有者CDO证券的投资者蒙受亏损。

因此，对合成型CDO的定价，首先也取决于对CDS如何定价。如何对CDS和CDO进行定价，依然是当前国际主流金融学杂志探讨的热点问题。

首先分析CDS的定价。根据资产定价理论，任何金融产品的市场价值都等于一系列未来现金流的折现价值。一份CDS合同通常面临两种现金流，一种是固定的保费支出(a fixed premium)，另一种是可能发生的赔偿收入(a contingent payment)。CDS的定价实质上是设定CDS的息差(保费费率)，而息差设定的标准是使得保费支出的现值等于赔偿收入的现值，即CDS 交易的净现值应该等于零。

在计算CDS价格时，最重要的两个参数P(0,t)和Q(t)需要通过历史数据模拟计算得到。举例而言，一种简化的方法是假设利率和违约概率服从一定的随机过程。例如对利率而言，可以假设利率满足如下的随机微分方程。

drt=a(b-rt)dt+σdzt

通过历史数据分析，可以计算得到相关参数，然后利用这种模型趋势可以预测未来利率走势，再进一步通过利率和零息债券的价格关系可以计算得到未来零息债券的价格走势p(0,t)。对违约事件而言，可以假设违约事件服从以h(t)为密度的Possion分布，h(t)满足如下关系

dIn(ht)=a(b-In(ht))dt+σdzt

相应的Q(h,t)可以通过如下模型计算得到

此次次贷危机涉及的另一种衍生品是CDO。在CDO的定价过程中有四个关键要素，分别是每个借款人的违约概率(Probability of Default，PD)、每笔债权的名义价值(Notional Value，NV)、每笔债权的回收率(Recovery Rate，RR)，以及借款人之间的违约相关性(Default Correlation)。前三个因素决定了特定借款人的违约风险可能造成的损失，即PD×NV×(1-RR)。而违约相关性假定则决定了在同一个时点，CDO信用资产池中的所有资产发生违约的概率是多少，从而得出损失的潜在分布(Potential Loss Distribution)。单个借款人的违约概率和回收率可以从该借款人的信用评级(即历史数据)中获得，每笔债券的名义价值不言自明，因此，在CDO的定价过程中，最为关键的是如何对借款人的违约相关性作出假定。

对CDO的定价常用的方法有蒙特卡罗模拟法、因子Copula模型法和静态价差法，目前，因子Copula 模型法已经成为国际上通行的CDO定价方法。本文主要介绍这种方法。

首先计算单个资产的违约概率。假设资产是否违约取决于该资产在特定时期(0,T)内的资产收益率。当资产收益率低于一定的阈值时，认为资产在T时之前已经违约。

资产的收益率受两部分因素的影响，一部分是系统因子，一部分是异质因子。系统因子部分反映了系统风险，也就是市场整体对资产回报率的影响，而异质因子则反映的是影响资产收益率回报的个别因素。一般假设系统因子和异质因子是随机的，而且服从正态分布(也可以是其他分布，如t分布)。

那么资产收益率可以用单因子的高斯Copula表示成：

这里，X与Yi均服从N(0,1)分布，而且两者相互独立，资产i与资产j之间的相关系数为ρiρj，于是在系统因子X确定的情况下，资产i的违约概率可以表示成：

再计算资产池的违约概率。假设资产组合中的所有资产均是同质资产，因此所有资产收益率与市场的相关性应该相等，假设为ρ，所有的违约阀值均为c,于是所有资产的条件违约概率为：

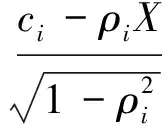
假设资产组合中有N个资产，如果有n个资产违约，则资产组合的违约损失率为：

由于上式是条件概率，对(4)式进行积分，则对所有的宏观情况有：

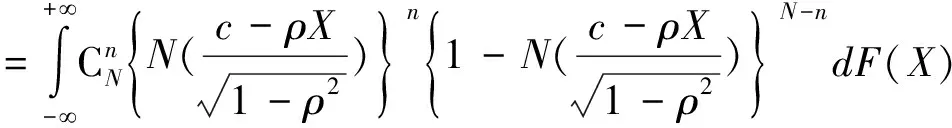
很显然P(n个违约)=P(L=L(n))。

对上式进行操作时，只需要知道相关系数与违约的閥值即可。

一般来说，对违约阀值c，由于假设系统因子X和异质因子Y均服从正态分布，那么资产回报率R也服从正态分布，假设单个资产的违约概率为p，则违约的阀值为c=N-1(p)，因此求违约阀值即求违约概率p。因此关键在于违约概率和违约相关系数的确定。

接下来就可以为CDO的定价。以最常见的CDO为例，假设CDO某层债券吸收整个资产池Q1到Q2比率的损失，于是当组合的损失率为L时，(Q1,Q2)层债券遭受的损失为:Loss(Q1,Q2)(LGD)=max {min (LGD(n),Q2)-Q1,0}，一般来说，如果知道了资产组合整体的损失率分布，就可以计算出(Q1,Q2)层债券的预期损失率为：

对于CDS 产品来说，投资者在投资信用产品时承受了信用风险，当然也要相应的风险溢价作为补偿，该补偿就是信用互换买方向卖方定期支付的利差。对CDO产品来说，投资者一方面承受来自资产池违约带来的违约损失，一方面也获得较一般债券更高的收益率作为补偿。在风险中性条件下，只有利差收益的补偿能弥补预期损失，投资者才有动力进行CDS或CDO产品的投资。即：预期违约损失=信用利差收益。

对无本金交割的CDO产品，假设CDO某层债券吸收整个资产池Q1到Q2比率的损失，那么对于该层债券信用利差收益将是未来预期信用利差的现值。

预期违约损失通过下式计算如下：

这里，0<=t0<…

因此根据无套利原理得到所求的信用价差：

在现实中，当CDO到期时如果存在本金支付时，CDO各档的债券价格可以表示为：

这里V(Q1,Q2)(0)表示债券价格，coupon为要求的票面利率。

从CDS和CDO的定价角度分析，上述定价方法主要有如下几个问题。

1.在对CDS和CDO进行定价时，通常假设贷款者有能力偿还贷款，从而有稳定的现金流，这是定价的基础，而真实情况是美国房地产市场的价格突然非预期的下跌，造成了大量信用违约事件。2000年到2006年的六年间，美国房地产市场持续繁荣，房价指数保持在10%的增长率，现房销售基本保持正增长，特别在2004至2006年间，现房销售同比增长率在10%附近浮动，一度曾超过20%的增长率。然而从2006年开始，美国房地产一路下跌，房价指数同比增长从15%的增长高位连续下跌到-10%附近。目前对违约概率和违约损失的估计有相似案例搜索，回归和模拟等方法，无论采用哪种方法，如果采用06年以前的数据构建模型对未来预测，由于06年以前的数据都在10%以上，模型无法计算出目前房地产市场的负增长状况，从而造成了模型对未来违约估计失效的情况。进一步，模型对违约相关参数的严重估计偏差将影响信用违约互换产品的定价，造成模型定价偏误。

2.在对CDS和CDO进行定价时，对折现因子的计算需要用到未来的利率，这种利率通常是通过历史数据建立数学模型计算得到，无法将影响利率的重要因素，例如未来宏观调控方向和力度等完全涵盖。从2004年6月30日到2006年6月29日，美联储连续加息17次，联邦基础利率从40年来的最低点1.25%上升至5.25%。模型在历史利率持续走低的情况下，很难预测得到这种持续上扬的情况，造成模型定价偏误。

3.CDO有一个重要参数是违约相关性，目前模型对违约相关性的处理是利用历史数据计算，但事实上违约相关性随市场环境等不断变化，历史信息无法反映所有情况，当市场出现逆转时，历史的违约相关性与实际违约相关性存在着重大的偏差，导致定价存在一定偏误。

4.从上面CDO和CDS的定价模型可以看到，模型中参数都是以其当前标底资产的属性作为输入参数，而卷入危机的很大一部分衍生产品的标底资产本身又是衍生产品。市场参与者由于无法掌握再上一层标底资产的状况，无法对它们的属性(例如违约率、违约损失率)直接进行估计，只能在一定的假设之下根据市场交易的信用价差来估计这些参数，而这种市场交易的信息价差只能反应对应层次市场参与者的判断，不能反应该衍生产品所包含的完整信息。随着衍生链条的加长，这种参数估计的偏差会越来越大。

5.市场参与者对于衍生链条上各层次衍生产品信息价差的判断，主要依据相应衍生产产品的信用评级。一方面如上述而言，由于对违约率、违约损失率的估计不准确，评级机构对于衍生产品的信用评级难以准确；另一方面，评级结果是由人决定的，由于评级机构不受监管，评级机构与被评级机构的利益相一致，于是就造成评级结果的高估，次贷担保债券的90%被授予AAA级，而美国非金融企业发行的证券中只有很小很小的比例能得到AAA级，出现了次级债务担保的风险和财务最健全的公司债券的风险处于同一等级这种明显不合理的现象。而这些却不是金融数学模型能够控制的。

6.上述模型只考虑了信用风险，而实际中的流动性因素没有被充分考虑。事实上，CDO产品是一种高度个性化的产品，一般被设计用来满足某个机构的需求，CDO大多数只被设计给“买入持有”型的投资者，比如养老基金，保险公司等机构。这些机构正是看准了这种产品的高收益与高信用评级的特征，而低的流动性意味着，一旦这些机构在CDO火爆的时候持有了过多的CDO，以后脱手将十分困难，市场参与者的同质性又使CDO的流动性进一步降低。 因此当实体经济的还款拖欠也就是信用风险被CDO放大过后，CDO的价值会急剧缩水，流动性几乎丧失殆尽，随后，信用衍生品市场开始动荡，而这反过来影响投资者的信心，导致投资者对风险进行重估，危机开始蔓延，投资者开始千方百计的拒绝任何高风险的固定收益品种，致使许多信贷行的对冲基金价值缩水，而这进一步加重了投资者的忧虑，引发新一轮的风险重估。

四、对金融数学发展及金融数学应用的启示

金融数学的运用失当，在某种意义上而言，对这次次贷危机起到了一定的推波助澜的作用。尽管相对于造成次贷危机的其他众多因素，金融数学的作用可能是最小的，但这促使我们去思考金融数学的未来发展。

首先，人类有史以来，数学的主要应用领域是物理和工程。数学对物理与工程中问题的描述相当成熟，从天体运行到微观粒子，从航天飞机到三峡大坝，数学已成为人类认识自然改造自然最有力的工具。但是利用数学对人类社会活动的描述，特别是金融数学，如果从BS期权定价公式开始算起，只是短短三十多年的时间。自然界的历史悠久，几十亿年的演化，其运动规律比较稳定，因此其数学描述也有一定的稳定性。然而人类整个历史不过上百万年，人类文明史不过几千年，人类市场经济历史不过几百年，人类的衍生品交易历史不过几十年，现代金融还处在快速演化之中，而致力于衍生产品定价的金融数学还只是这演化中的一部分。因此金融数学在衍生产品定价上出现偏差是再正常不过的。金融数学不是发展过度，恰恰是发展不足。次贷危机带给我们的启示之一是需要大力发展金融数学。

其次，要认识到金融数学的局限性。不仅要认识到金融数学本身发展阶段的局限性，认识到它还不能像工程数学解决工程问题那样可靠地解决金融问题，而且要认识到现在的金融数学模型本身并非万能的局限性。衍生品定价中的金融数学模型是在已有信息集下采用某种方法对未来未知的情况做出判断。这里有两个关键因素，第一是信息集；第二是采用的方法。对于信息集而言，无论如何努力搜集整理信息，信息总是不完全的，特别是未来的信息，总是我们无法掌握的，即无法得到足够充分的信息将所有的未知转化为已知。这种信息的不完全性决定了模型对未知的估计总会存在偏误。第二，采用的方法上，没有绝对万能的模型和方法，每一种方法都有其自身的严格假设和前提，当环境变化，这些假设和前提条件不再成立时，方法和模型也就出现了问题。

再次，如同数学可以精确地计算运载火箭的轨道，但不能决定运载火箭何时发射、目标是哪里、是装载核弹头还是装载气象卫星一样，金融数学模型也不能决定模型的具体运用是为了提高整个社会所有成员的福利，还是被用来谋取少数人眼前的利益。金融危机的产生一方面存在着其历史必然性，另一方面也缘自人类自身的贪婪行为。可以断言，无论金融数学如何发展，都不可能杜绝金融危机的发生。金融数学是人类认识问题和分析问题的一种工具，它拓展了人类智慧，推动着人类社会的总体进步；金融数学的发展不会因为这次危机而停步，今后有更加广阔的空间和更好的发展前景。

[参考文献]

[1]Black, F. and J. C. Cox, 1976, “Valuing Corporate Securities: Some Effects of Bond Indenture Provisions”, Journal Finance, 31/2, pp. 361-67.

[2]Das, S., 1998, Credit Derivatives: Trading & Management of Credit & Default Risk, John Wiley & Sons.

[3]Das, S., and P. Tuffano, 1996, “Pricing Credit Sensitive Debt when Interest Rates, Credit Ratings and Credit Spreads are Stochastic”, Journal of Financial Engineering, 5, pp. 161-98.

[4]Duffie, D. and K. J. Singleton, 1996, “Modeling Term Structures of Defaultable Bonds”, Graduate School of Business, Stanford University.

[5]Hull, J., 1993, Options, Futures, and other Derivative Securities, Prentice-Hall.

[6]Jarrow, R. and S. M. Turnbull, 1995a, “Drawing the analogy”, Risk, 5, pp. 63-70.

[7]Jarrow, R. and S. M. Turnbull, 1995b, “Pricing Derivatives on Financial Securities Subject to Credit Risk”, Journal of Finance, 50/1, pp. 53-86.

[8]Jarrow, R., D. Lando and S. M. Turnbull, 1997, “A Markov Model for the Term Structure of Credit Risk Spreads”, Review of Financial Studies, 10/2, pp. 481-523.

[9]Lando, D., 1994, “Three Essays on Contingent Claims Pricing”, PhD thesis, Cornell University, Ithaca, N. Y.

[10]Longstaff, F. A. and E. S. Schwartz, 1995, “A Simple Approach to Valuing Fixed and Floating Rate Debt”, Journal of Finance, 50, pp. 789-819.

[11]Longstaff, F. A., and E. S. Schwartz, 1995, “Valuing Credit Derivatives”, Journal of Fixed Income,5-1, pp. 6-12.

[12]Merton, R. C., 1974, “On the Pricing of Corporate Debt: The Risk Structure of Interest Rates”, Journal of Finance, 29, 449-70.

[13]Monkkonen, H., 1997. Modeling default risk: Theory and empirical evidence. Ph. D. Thesis,Queen’s University, Kingston, Ont.

[14]Skora, Richard K., 1998, “Rational Modelling of Credit Risk and Credit Derivatives” working paper.

[15]Agnieszka Zalewska,2004, Modelling the Price of a Credit Default Swap,KTH numerical analysis and computer science.

[16]陈田，秦学志.债务抵押债券(CDO)定价模型研究综述[J].管理学报，2008，(6).