中考规律探索型试题赏析

张符艳

规律探索型试题是近几年中考出现的热点题型之一,其特点是:给出一组具有递进关系的数、式子、图形或某个由简单到复杂的操作过程,或某一具体的问题情境,通过探求其变化过程中的规律,归纳或猜想出一般性的结论。这类题立意新颖、灵活多变,渗透了类比、归纳、分类讨论、数形结合等数学思想,备受命题者的青睐。

题型一:关于数字问题的猜想

(2009年恩施州)观察数表,根据表中数的排列规律,则字母A所表示的数是____。

分析:从图形中看出,两侧都是1,中间数的绝对值都是上边相邻两个数字的和,每行第偶数个数字的符号为负,奇数个符号为正。

答案:10

方法点拨:本题是关于数字问题规律的探索,题目利用问题叙述和图形结合命制,考查数形结合思想和归纳探索能力。对于数字猜想问题,通常可以从数列的角度来考虑,即找到第一天或第一列对应的数,再找到第二天或第二列对应的数,依次类推,根据所得数的规律探寻一般的规律。

题型二:关于等式问题的猜想

(2009年河年)古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”。从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和。下列等式中,符合这一规律的是()

A.13=3+10 B.25=9+16

C.36=15+21 D.49=18+31

分析:此题关键是理解“正方形数”和“三角形数”这两个从图形组合的角度给出的概念。

答案:C

(2009年重庆)观察下列等式:

①42-12=3×5; ②52-22=3×7;

③62-32=3×9; ④72-42=3×11;

……

则第n个等式为_____。

分析:从上式关系来看,等式左边第一列分别为4,5,6,7连续数列的整数,第二列从1,2,3,4开始,右边的第一列为3,第二列为5,7,9,11连续数列的奇数,恰为等号左边两个底数的和。

答案:(n+3)2-n2=3×(2n+3)

方法点拨:关于等式的问题,我们要注意观察等式中各部分变化与等式所在的项数的关系。解这一类题目,要用到归纳推理,它是一种重要的数学思想方法。学习数学必须不断的探索、猜想,不断总结规律,才会有所发现、有所创新。

题型三:关于图形排列规律的猜想

(2009年长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为(用含n的代数式表示)。

分析:根据图形可知,①中有4个正三角形②中有6个③中有8个按此规律④为4+3×2=10。按此方式可求出第n个图案中正三角形的个数为4+2(n-1)。

答案:2n+2

方法点拨:将抽象的数或是通过一组图形具体化,再从图形中抽象出数或式,要求具备一定的抽象转化能力,把问题定位到恰当的模型中。此题旨在引导学生关注生活,增强“做数学,用数学”的意识。

题型四:关于数形结合的规律

(2009年台州)将正整数1,2,3,…从小到大按下面规律排列。若第4行第2列的为32,则①n=;②第i行第j列的数为 (用i,j表示)。

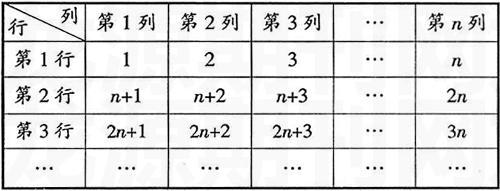
分析:按照“特例助思”,第4行第2列为3n+2,令3n+2=32,则n=10;此题每一行第一个数为(行数-1)n,第二个数为列数,第n行n列的数为这两个数的和。

答案:10;10i+j-10

方法点拨:本题是关于数列与有序实数对之间的问题。此类题目可用两种方法处理,其一是当数较小时,可直接列出全部的数,其二是找到一般规律,再找到特殊情况所对应的数。

作者单位:河北省迁安市西里铺中学