基于系统动力学的航空兵作战油料保障决策模型研究

陆思锡 周庆忠 杨凌峰

摘要:运用系统动力学原理及VENSIM建模平台建立了航空兵作战油料保障的仿真决策模型,以航空兵场站油料存储量为切入点,将航空兵作战油料保障的各种要素结合起来。通过实例仿真,分析了两个重要参数值的改变对仿真结果的影响,并确定出其对油料保障效率的影响程度,从而为航空兵作战油料保障提供科学的定量决策依据。

关键词:航空兵;油料保障;决策;系统动力学;仿真

中图分类号:E234文献标识码:A

Abstract: This paper has established a simulation decision-making model of air arm POL(Petrol Oil and Lubricants)service in wartime, which is based on system dynamics and the modeling platform of vensim, and has taken the POL storage of air arm aerodrome as a cut-in point to combine all kinds of factors in the POL service. The influence of simulation result which caused by the change of two important parameters has been analyzed by simulating an example, and the influence degree of POL service efficiency has also been confirmed, which offers scientific and quantificational decision-making basis to the air arm POL service in wartime.

Key words: air arm; POL service; decision-making; system dynamics; simulation

0引言

航空兵部队是重要的空中作战力量,其作战效能直接影响到我方对制空权的控制,以及与其他军兵种协同作战的效果。油料保障,作为航空兵作战重要的后勤保障工作之一,对航空兵作战效能具有重要影响。科学、合理地油料保障决策可以为航空兵部队提供更加高效、可靠的战时油料保障,从而提高航空兵部队的整体作战效能。因此,研究航空兵作战油料保障决策问题具有十分重要的理论和现实意义。

在信息化战争条件下,战场环境的透明化、不确定性以及空间转换节奏的加快,使航空兵作战油料保障呈现出更加复杂的动态性,增加了油料保障的难度,对油料保障决策者提出了更高的要求[1]。对于信息化战争条件下动态变化的航空兵油料保障决策问题,传统的静态方法很难凑效,而系统动力学(System Dynamics)则为解决动态复杂性问题提供了一种可行的理论与方法。系统动力学是美国麻省理工学院的福瑞斯特(Jay W. Forrester)教授于1956年创始的一门分析研究信息反馈系统的学科,它综合了反馈控制论、信息论、系统论、决策论、计算机仿真以及系统分析的实验方法,利用系统思考的观点来界定系统的组织边界、运作及信息传递流程,以因果反馈关系描述系统的动态复杂性,并建立量化模型,利用计算机仿真方法模拟不同策略下现实系统的行为模式,最后通过改变结构,帮助人们了解系统动态行为的结构性原因,从而分析并设计出解决动态复杂问题的方案[2-4]。

为了把决策建立在更加科学的基础之上,本文将航空兵作战油料保障作为一个系统来分析,以系统动力学理论为工具,对航空兵作战油料保障进行仿真建模研究。

1航空兵作战油料保障动力学模型的建立

1.1模型假设

由于对航空兵作战油料保障的仿真建模是一项复杂的系统工程,需要对某些影响因素进行一些合理的假设才能使问题更好地得到解决,因此对模型的建立作出了如下假设:(1)只考虑对单一机种的油料保障情况。(2)航空兵油料保障在时间上是连续的。(3)作战飞机的战损情况服从一定规律。(4)不考虑对作战飞机数量的增援。(5)忽略油料保障人员及设施设备的战损情况。

1.2流图的建立及主要方程的确定

1.2.1流图的建立

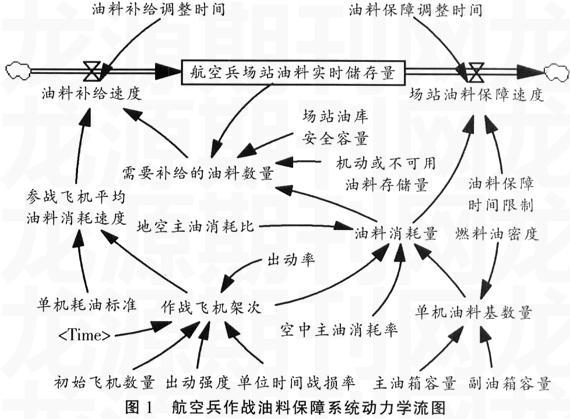
航空兵场站油料实时存储量、场站油料保障速度、油料消耗量、需要补给的油料数量、油料补给速度等是影响航空兵作战油料保障的几个主要因素,下面将着重对这几个变量及相关影响因素进行分析。

(1)模型中的流位(Level)变量为航空兵场站油料实时存储量,它由流率(Rate)变量场站油料保障速度及油料补给速度共同决定。

(2)场站油料保障速度由油料消耗量和油料保障时间限制共同决定。其中,油料消耗量由作战飞机架次、空中主油消耗率、单机油料基数量决定。

(3)油料补给速度由需要补给的油料数量和参战飞机平均消耗速度决定。其中,需要补给的油料数量由场站油料存储量、油料消耗量、场站油料安全存储量、机动或不可用油料存储量共同决定。

通过上述分析,利用VENSIM平台构建的模型流图如图1所示。

1.2.2主要方程的确定

在确定作战飞机架次时,考虑到飞机的战损情况,选用了指数函数来描述飞机数量的变化情况;在油料补给速度的关系式中,采用了IF THEN ELSE函数,其目的是保证在各个阶段都是以最快的速度进行油料补给;考虑到油料保障具有一定的滞后性,在保障速度的关系式中采用了平滑函数SMOOTH来实现。

模型中的关键数学关系式如下:

(1)航空兵场站油料实时储存量=INTEG(油料补给速度-场站油料保障速度)

(2)需要补给的油料数量=场站油库安全容量+油料消耗量-航空兵场站油料存储量-机动或不可用油料存储量[5]x

(3)油料消耗量=单机油料基数量*空中主油消耗率*作战飞机架次*(1+地空主油消耗比)[5]

(4)作战飞机架次=初始飞机数量*出动率*出动强度*(1-单位时间战损率)^ Time

(5)油料补给速度=IF THEN ELSE(参战飞机平均油料消耗速度/(需要补给的油料数量/油料补给调整时间)<1,需要补给的油料数量/油料补给调整时间,参战飞机平均油料消耗速度)

(6)场站油料保障速度=SMOOTH(油料消耗量/油料保障时间限制,油料保障调整时间)

2实例仿真分析

下面以某次作战某航空兵场站对进驻部队的某一机种进行油料保障为例对模型进行仿真分析。

2.1仿真条件

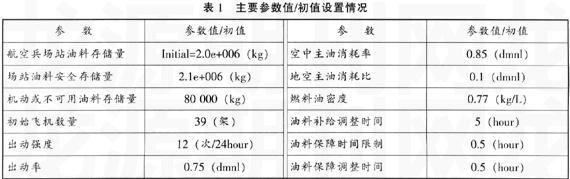
模型的运行环境参数设置分别为:INITIAL TIME=0,FINAL TIME=240(hour),STEP TIME=1(hour),即仿真的时间为10天,步长为1小时,各参数及初值设置如表1所示。

2.2仿真结果输出

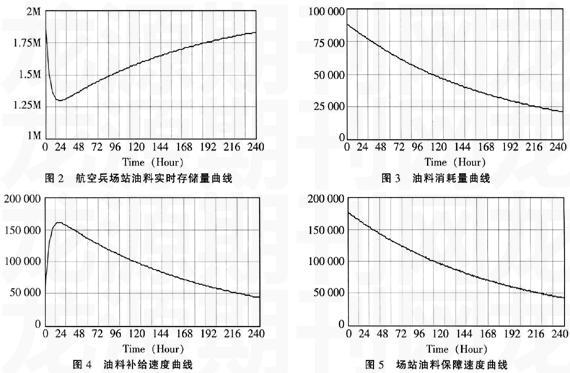
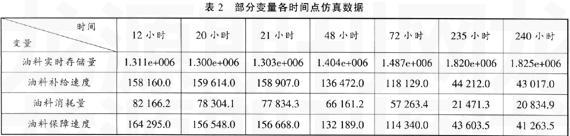
通过运行VENSIM得到航空兵场站油料实时存储量、油料消耗量、油料保障速度、油料补给速度的仿真曲线如下图所示,部分仿真数据如表2所示。

2.3仿真结果分析

(1)从图2可以看出,在作战开始的20小时内,油料存储量迅速减少,最低存储量为1.3e+006kg。这是由于在作战开始阶段参战飞机数量较多,战况较为激烈,因此耗油量较大,同时,油料补给速度在作战开始的20小时内小于油料保障速度,从而导致场站油料存储量在作战开始的20小时内迅速下降。在作战20小时之后,由于作战飞机数量的减少,且随着时间的推移,战况激烈程度明显降低,油料消耗量开始减少,同时,油料补给速度在作战20小时后与场站保障速度基本保持了同步,因此场站油料存储量在20小时后开始逐步回升,并在235小时以后趋于稳定。

(2)从图4可以看出,油料补给速度在作战开始的20小时内迅速增加,这是由于存储量迅速减少,需要对场站油料存储量进行补给,而只有依靠提高油料补给速度才能达到补给效果。当补给速度增加到与保障速度相当的时候,随着油料消耗量的减少,油料存储量开始稳定,这时对油料补给速度的要求就没有开始阶段时高,因此油料补给速度开始与油料保障速度呈相似的变化规律,并逐步降低,在230小时后趋于稳定。

2.4参数值的改变对仿真结果的影响分析

在仿真过程中我们发现,油料补给调整时间和油料保障时间限制这两个参数对航空兵作战油料保障效果的影响较大,其分别影响油料补给速度和油料保障速度这两个变量,从而进一步影响场站油料存储量。因此,通过控制这两个参数,就可以提高油料保障的效率;分析其对油料保障的影响,就可为决策者提供可靠的决策依据。下面分两种情况着重就时间参数的设置对仿真结果的影响进行讨论。

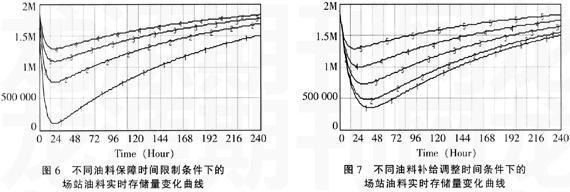
(1)将油料保障时间限制每次减少0.1小时,其它参数值与2.1节设置一致,得到不同油料保障时间限制条件下的场站油料实时存储量仿真结果如图6所示。图中曲线1～4分别表示油料保障时间限制分别为0.2、0.3、0.4、0.5小时的油料实时存储量。从图中可以看出,参数值的改变对油料实时存储量在开始阶段的减少量影响较明显,曲线1与曲线4的对比尤为明显。当油料保障时间限制从原来的0.5小时调整为0.2小时后,相当于提高了油料保障速度,但油料补给速度并没有提高,从而使得油料支出量大于油料补给量,油料实时存储量比调整前减少得更多,因此出现不能满足作战油料保障需求的情况。

(2)将油料补给调整时间从5小时每次增加2小时至12小时,其它参数值与2.1节设置一致,得到不同油料调整时间条件下的场站油料实时存储量仿真结果如图7所示。图中曲线1～5分别表示油料补给调整时间为12、11、9、7、5小时的场站油料实时存储量。从图中可以看出,油料存储量在开始阶段随调整时间的增加而减少得较为明显。当油料补给调整时间从5小时调整为12小时后,相当于降低了油料补给速度,同时由于油料保障速度保持稳定,从而使得油料补给量小于油料支出量,场站油料实时存储量减少较快,不能满足作战油料保障的需要。

2.5油料保障决策分析

从2.4节的分析中可知,油料保障时间限制和油料补给时间是两个非常重要的参数值,改变这两个参数值,将影响航空兵作战油料保障的整体效率,因此,在进行油料保障决策时,需要合理地确定这两个参数值,才能使油料保障获得最佳的效果。在确定这两个参数值时,既要考虑到时效性,又要考虑到战时的实际情况,如果把油料保障时间限制确定得太短或者将油料补给调整时间确定得太长,都会增加油料保障难度,降低油料保障效率。从2.4节的分析来看,油料保障时间限制不应低于0.2小时,同时考虑到战时对时间要求较高,因此,油料保障时间限制不应超过0.5小时。同理可以分析出如果油料补给调整时间太短,不仅不利于本级油料保障,还会给上级油料调运增加很大难度,因此结合战时的实际情况(如敌方对我打击等造成的战损情况)考虑,调整时间不应低于5小时,同时考虑到战时的时间限制,调整时间不应超过12小时。此外,在作战开始的20小时内,由于诸多不确定因素的存在,油料消耗量将比预期更大,因此,应采取措施加强这段时间内的油料补给。例如,开设野战油库储油、利用野战输油管线进行油料补给等,以确保油料保障工作的顺利进行。

3结束语

本文以航空兵场站油料实时存储量为着眼点,将油料保障过程作为一个系统来考虑,利用系统动力学的方法对航空兵作战油料保障进行了建模与仿真,并分析了参数值改变对油料保障的影响,为航空兵作战油料保障提供了定量决策依据。由于时间、条件和作者能力有限,文章尚存在构建的模型深度和广度不够、反馈控制理论与数学知识的应用不够等不足之处,这些都有待在后续的研究中进一步完善。

参考文献:

[1] 冯刊民,王丰. 高技术条件下空军战役油料保障研究[M]. 北京:解放军出版社,2003.

[2] 贾仁安,丁荣华. 系统动力学——反馈动态性复杂分析[M]. 北京:高等教育出版社,2002.

[3] 王其藩. 高级系统动力学[M]. 北京:清华大学出版社,1995.

[4]Forrester J W. Industrial dynamics[M]. Cambridge Mass: MIT Press, 1961.

[5] 于贤福,李选民. 空军油料勤务学[M]. 北京:蓝天出版社,1997.