姿态四元数相关问题

马艳红 胡 军

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190）

姿态四元数相关问题

马艳红1，2胡 军1

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190）

介绍了四元数计算中的相关问题，包括四元数与方向余弦阵之间的转换、四元数运动方程、求解四元数运动方程时积分步长的选取和高动态应用中非互易误差的补偿，此外还介绍了对偶四元数的发展。

姿态确定；方向余弦矩阵；四元数；非互易误差；对偶四元数

1 引 言

自1843年Hamilton首先在数学中引入四元数［1-2］以来，直到20世纪六七十年代这一方法才在控制工程中得到实际应用。作为描述刚体旋转运动的方法之一，四元数在计算方面具有其优越性：四元数的描述中只有一个冗余参数，省去了欧拉角三角函数的繁琐运算，减轻了计算机的负担；四元数的运动方程为线性方程，不会出现奇异，避免了飞行器大姿态时的欧拉角退化问题。早在1971年，美国的空间实验室（Skylab）就采用四元数来描述旋转运算，完成实验室的在轨组装［3］。近年来基于四元数的飞行器控制和滤波技术得到了广泛关注［4-6］。

四元数是继复数之后的一个新数系［2］，即任意两个四元数的加、减、乘、除仍然是一个四元数，文献［7-8］对四元数的各种运算及其几何意义做了详细阐述。一个四元数可以分为标量和矢量两个部分，记为

若将其矢量部分投影到某坐标系I中，则得到四元数在 I坐标系中的“映像”［8］，记为

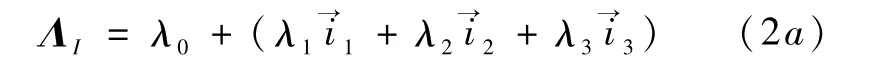
或

与复数类似，四元数的共轭运算定义为

四元数乘法定义如下

由式（4）可知，四元数乘法具有其特殊性，它满足“模法则”但是不满足交换律，即

其中

采用单位四元数描述旋转运动，即

由于Q和 -Q旋转结果相同，一般取 q0≥0，称为“标准四元数”，此时姿态的四元数描述具有唯一性。

2 姿态四元数与方向余弦阵之间的转换

描述飞行器姿态的常用方法有欧拉角、欧拉轴/角和方向余弦阵，它们与四元数之间的转换有多种方法，现在仍有部分文献研究各描述方法之间的转换［9-10］。

以方向余弦阵为例，其中最有效的是1978年Shepperd提出的转换方法［11］。文献［8］从矢量旋转和坐标系旋转两个角度给出方向余弦阵和四元数之间的转换关系，本节将结合文献［11］中的内容，对这两种转换进行分析。

2.1 基于矢量旋转的转换方法

其中

其中，I3×3表示 3×3的单位矩阵，C=［cij］（i=1，2，3；j=1，2，3）。

依据文献［11］的方法给出方向余弦矩阵到四元数的转换Rc2q（C）。给定四维向量

其中tr C表示C矩阵的迹。取

则

其中

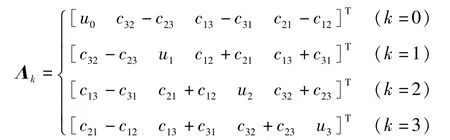
若将式（7）代入式（8）可知

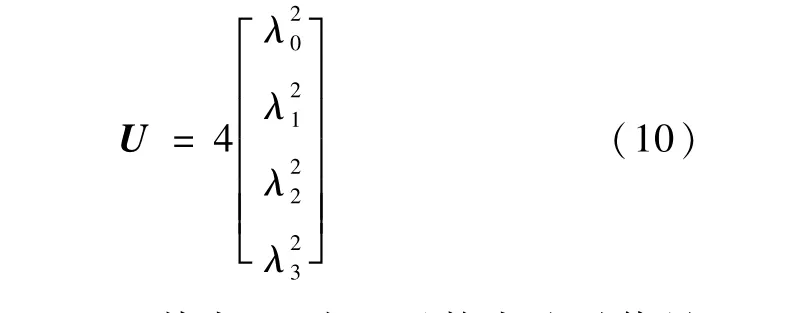
因此有 Λk=4λkλ≠0，其中 λk为四元数中绝对值最大的分量，必有，从而有‖Λk‖≥2。用上式提取四元数非常可靠，因为在求取‖Λk‖时根号下不可能为负，因此该方法在使用前无需对C矩阵进行正交规范化处理。

2.2 基于坐标系旋转的转换方法

设用四元数Q表示从坐标系I旋转到坐标系E，对于某矢量r→，在I中的投影为ri，在E中的投影为re，此时四元数在I和E中的“映象”相同。四元数与方向余弦阵之间的转换式如下

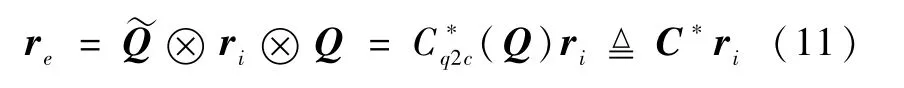
相应的方向余弦阵到四元数的转换

其中

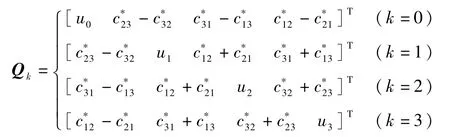
uk的定义同式（8）。

2.3 两种转换之间的关系

在航天器姿态确定和控制［4-6］中，常采用的是基于坐标系旋转的转换方法，若取I系为轨道坐标系，E系为航天器本体坐标系，则得到飞行器的姿态四元数，相应的四元数与方向余弦阵通过式（11）和式（12）实现相互转换；而在捷联惯导系统［10-12］中，常采用基于矢量旋转的转换方法，依据式（8）和式（9）实现四元数和方向余弦阵之间的转换。

为说明这两种转换之间的关系，我们采用欧拉轴/角来表示四元数，称之为“欧拉-罗得里格四元数”（Euler-Rodrigues quaternion）或 “特 征 四 元数”［8］。设表示旋转的欧拉轴/角为（e→，θ），则相应的四元数可表示为

由式（7）可得：连续旋转 Λ1，Λ2，…，Λn等价于一次旋转运算 Λn⊗Λn-1⊗…⊗Λ1。由式（11）可得：连续旋转 Q1，Q2，…Qn等价于一次旋转运算Q1⊗Q2⊗…⊗Qn。

3 四元数运动方程

早在1964年，Stuelpnagel就指出：对于描述三维转动的各种参数，3个参数得到的必是非线性运动学方程，要得到线性方程，至少要采用4个参数。依据角速度在动坐标系和参考坐标系中不同的投影，可以得到两组不同的四元数更新方程［13］。

“角速度”是理论力学中一个基本概念，迄今仍有部分文献研究角速度的物理概念和特性［14-15］。运动刚体的角速度一般有两种引出方法［16］：一种是基于欧拉有限位移定理，利用绕转轴的有限角位移定义“平均角速度”，然后在△t→0时取极限得到“角速度”；另一种是利用坐标转换矩阵的正交性，定义反对称的“角速度张量矩阵”，然后依据运算的等价性定义“角速度矢量”。

此处依据“角速度”的第二种定义方法给出四元数的运动方程。取参考坐标系（固定坐标系）为I，动坐标系（固连坐标系）为 E，两坐标系的基分别为［8］

则有方向余弦阵

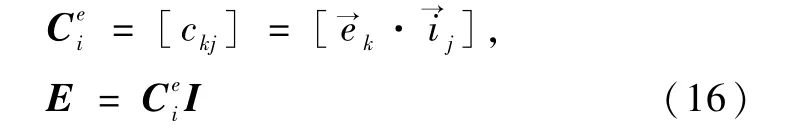
其中

从而有

若转动角速度在动坐标系E下的投影记为ωe，则

依据下式求解ωe

转动角速度在固定坐标系I下的投影记为ωi，则

依据下式求取ωi

依据式（20）和式（22）可以得到方向余弦阵的运动学方程。

上述方向余弦阵描述的是坐标系的旋转，因此相应的从I转到E的四元数描述为

得到的四元数运动学方程为

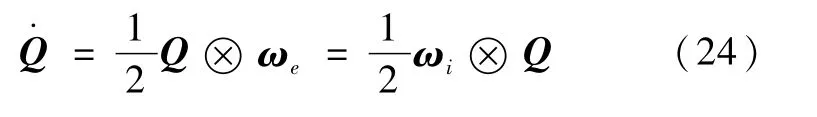
上式两边取共轭运算，可得到相应共轭四元数的运动学方程为

此处Q为坐标系旋转运动的四元数，则对应式（18）的四元数表述为

4 积分步长对四元数解算精度的影响

依据式（24）求解四元数运动方程时，ω是由陀螺测量得到的，因此无法得到它在任意时刻的值，而是得到它在采样周期内的平均值，所以积分解算后存在误差。另外，数值解算时也不可避免的存在截断误差，因此随着时间的推移，姿态四元数“模为1”的限制将不再得到满足。相关文献［20-21］的研究都表明四元数解算时对积分步长的要求比较严格。

在使用模拟计算机时，四元数模值漂移尤其严重，必须进行正交规范化处理［17-18］，又称为“归一化”处理；在使用现代数字计算机时，采用较小的积分步长和高阶的积分算法，四元数模值漂移速率很小。文献［17］指出：在利用四阶龙格库塔法进行四元数积分解算时，若每个采样周期内的转动角度为10°，则经过 3×106次迭代，四元数的模才会退化1%；因此在每个采样周期内的转动角度小于5°时，一般不作正交规范化处理，文献［19］也从数值仿真的角度给出了利用一阶差分法解四元数方程时，保证范数精度的步长约束条件，如下所示

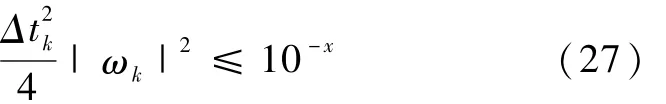
其中，x为所要求的精度指标，Δtk为积分步长，ωk为角速度。

文献［20］针对高动态运动采用龙格库塔法解算四元数，没有进行四元数的规范化处理。仿真结果表明：高动态时，虽然变步长方法不能消除由于四元数的模值漂移引入的误差，但相比定步长方法而言，可以有效抑制模值的漂移速度。文献［21］在进行四元数解算时同样没有进行正交规范化处理，针对高动态运动仿真得到如下结论：四元数法在时间步长较小时具有很高的计算精度，但是对时间步长的要求要比欧拉角法苛刻，步长较大时，欧拉角法的精度较高。

因此可见：采用高阶的算法或者采用较小的步长可以在一定程度上抑制四元数解算时模值的漂移，但是无法消除该漂移，因此若积分时间很长，则这一项的积累误差仍然不可忽略；另外，在高动态运动或者计算步长受限时，计算步长内四元数的变化较大，此时四元数模值的漂移也会比较明显。因此在用数值法求解四元数运动方程时，建议依据下式［17-18］周期性地对四元数进行规范化处理

文献［22］指出如果利用式（28）进行四元数规范化处理，就需要进行开方运算，从而增加了计算负担和程序中控制的复杂性，所以文献［22］还给出一套四元数的保范递推公式，它在计算量方面优于式（28）。

5 非互易误差的补偿

由理论力学可知：刚体的有限转动不是矢量，是不可交换的，也就是说两次以上的转动不能相加［16］，如

只有当 θ（t）和 Δθ方向一致时，式（29）才成立。在用数值方法解算方向余弦阵或四元数运动学方程时，都需要求解角速度的积分。设陀螺采样周期为Δtk，陀螺输出为采样周期内的角增量Δθk，若采样周期内角速度方向不变，则有

若运动方程的算法采样周期为ΔT，ΔT内有n个陀螺采样点，则利用计算机数值求解角速度积分的实质就是求和运算，如下所示

可见当Δθk为有限转动且方向各不相同时，式（31）不成立，也就是说对于一个方向随时间变化的角速度矢量进行数值积分是没有任何意义的。这种由于有限转动的非互易性（noncommutativity of finite rotation）引入的误差称为“不可交换误差”或“非互易误差”，文献［23-25］对上述误差的产生机理做了详细描述。

由上述分析可知：非互易误差属于算法误差，可以通过改进算法来减小这一误差，若ΔT足够小，使得ΔT上的有限转动近似为无限转动，则式（31）成立。受到计算能力的限制，ΔT总是有限的，特别是当系统高动态运动时，算法采样周期内角速度方向变化较大，此时“非互易误差”较大，必须进行补偿。

Bortz分别于1970年和1971年对“非互易误差”进行了分析，并提出了等效旋转矢量的概念［24-25］，其意义在于为每一次有限转动寻找一个等效的旋转矢量，使得各次转动形成的结果可以通过对等效旋转矢量进行矢量合成得到，即寻求Δθ的有效表示，使得式（29）成立，并以方向余弦阵运动方程为基础，推导得到 Bortz方程。文献［26］以四元数运动方程为基础，用同样的方法推导得到Bortz方程。依据式（13），定义等效旋转矢量为

则Bortz方程如下所示

其中σ即为非互易误差

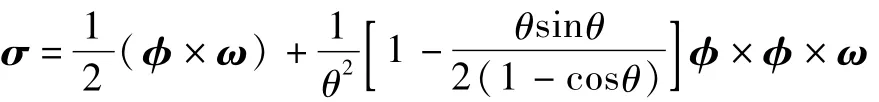
当θ很小时，近似有

此时可依据式（33）在算法采样周期内数值积分得到Δφ，文献［26］给出了两种采用 Δφ更新四元数的方法。

Miller等［27］学者在 Bortz方程的基础上先后提出了有效利用陀螺输出的多子样算法，且现在仍有很多文献在研究这类多子样算法的有效性［27-29］。所谓“多子样算法”即在算法采样周期内使用陀螺的多个输出信息，提高采样率，使角增量进一步实现微小化，从而使有限转动趋近于无限转动，减小非互易误差，其中算法采样周期内的采样点数被称为“子样阶数”。

文献［26］指出算法的子样阶数与运载体角速度曲线阶次的假设效果是相对应的：单子样算法对应角速度为常值的假设，在算法采样周期内进行一次采样，即只提取一个角增量，单子样算法即为四元数算法；双子样算法对应于角速度曲线为直线的假设；三子样和四子样算法分别对应于角速度曲线为抛物线和三次曲线的假设，对角速度做拟合时，曲线阶次越高，子样数越高，算法精度也越高。文献［28］给出了多子样旋转矢量法的一般结果，极大地方便了姿态算法的设计。

由式（32）可知，当 φ与ω垂直时，非互易误差σ最大，此时对应典型的“圆锥运动”（coning motion）［26-31］，因此一般采用圆锥运动来评价姿态算法的优劣。文献［29］对高动态环境下四元数的四阶龙格库塔法和三子样旋转矢量法进行了仿真比较，以典型圆锥运动为输入信号，以圆锥漂移为检验算法的基准，仿真结果表明：等效旋转矢量法对提高高动态环境下的导航精度具有更高的实用价值。

“非互易误差”和“圆锥误差”虽然有联系，却是两个不同的概念，文献［30-31］在分析圆锥运动的基础上指出：非互易误差属于算法误差，与是否做圆锥运动无关，圆锥运动本身不会给导航解算带来误差；而“圆锥误差”是指在圆锥运动下所引起的导航计算误差。

6 对偶四元数

作为空间运动学基本原理之一的Charles定理指出：一般性刚体运动包括一个绕某个轴的旋转和沿该轴的平移，因此一般性刚体运动又被称为“螺旋运动”［32］。常用分析方法是将螺旋运动拆分为定点转动和平移运动，并分别加以考虑。捷联惯性导航系统中也将姿态积分和速度/位置积分分开考虑，分别设计不同的算法。

1873年 Clifford提出对偶数的概念，并在此基础上建立了对偶四元数（dual quaternion），描述螺旋运动。对偶四元数是元素为对偶数的四元数，四元数的性质被对偶四元数完全继承，它的特点是可以把旋转和平移运动统一考虑，能够以最简洁的形式表示一般性刚体运动，数学表达式直观明了。20世纪中后期对偶四元数逐渐应用到各项工程领域中［32］。

1992年，联盟号宇宙飞船控制系统总设计师Branets把对偶四元数应用于惯性导航领域，首次论述了在捷联式系统的理论分析中引入对偶四元数代数的可能性，勾画了用对偶四元数描述捷联系统中各坐标系间关系的基本框架。2005年，武元新以对偶四元数理论为基础完善了Branets提出的捷联式惯性导航的对偶四元数代数描述，并在此基础上创造性地提出了基于双速结构的对偶四元数导航算法，揭示了传统算法中的圆锥算法和划船算法之间存在对偶性/等价性的根本原因，从理论上证明了在高精度和高动态环境中，对偶四元数导航算法的精度将优于传统算法［32］。

四元数的这一发展表明：四元数的优越性不仅体现在计算方面，它还能够以最简洁的形式描述一般性刚体运动，同时包括平动和转动，文献［32］对对偶四元数的发展和应用做了详细阐述。

7 结束语

在描述刚体姿态运动及其演化规律方面，四元数具有独特的优势，因而得到广泛应用。本文分析了四元数与方向余弦阵之间两种转换方法的区别和联系、积分步长对四元数运动方程解算精度的影响以及非互易误差产生的机理及其补偿策略，最后简单介绍了对偶四元数的发展。

［1］ Hamilton W R.Elements of quaternions［M］.New York：Chelsea，1969

［2］ 程小红.哈密顿与四元数［J］.数学通报，2006，45（6）：57-59

［3］ Whipple P H.The quaternion representation of rotations and its application in the Skylab orbital assembly［R］.NASA-CR-118019，1971

［4］ Choukroun D，Bar-Itzhack I Y，Oshaman Y.A novel quaternion Kalman Filter［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Reston，USA，2002

［5］ 朱庆华，李英波.基于陀螺和四元数的 EKF卫星姿态确定算法［J］.上海航天，2005，22（4）：1-5

［6］ George P D，Brett A N.The application of quaternion algebra to gyroscopic motion，navigation and guidance［C］.AIAA Guidance， Navigation and Control Conference and Exhibit，San Francisco，USA，2005

［7］ Meister L，Schaeben H.A concise quaternion geometry of rotations［J］.Mathematical Methods in the Applied Sciences，2005，28（1）：101-126

［8］ 勃拉涅茨，什梅格列夫斯基.四元数在刚体定位问题中的应用［M］.梁振和，译.北京：国防工业出版社，1977

［9］ Bar-Itzhack I Y.An algorithm for computing the quaternion from the rotation matrix［C］.AIAA/AAS Astrodynamics Specialist Conference， Reston，USA，2000

［10］ 周江华，苗育红，肖刚.捷联惯导系统初始四元数提取的新算法［J］.飞行力学，2003，21（3）：63-66

［11］ Shepperd S W.Quaternion from rotation matrix［J］.Journal of Guidance and Control， 1978， 1（3）：223-224

［12］ 毛克诚，孙付平.捷联惯导系统四元数转换误差分析［J］.测绘科学技术学报，2006，23（4）：284-286

［13］ Stuelpnagel J.On the parametrization of threedimensional rotation group［J］.SIAM Rev，1964，6（4）：422-430

［14］ 王侃，任革学，李俊峰，张雄.关于刚体角速度定义的一个注解［J］.力学与实践，2007，29（1）：71-72

［15］ 李海龙，水小平.一种引出一般运动刚体角速度概念的新方法［J］.力学与实践，2007，29（1）：73-74

［16］ 朱照宣，周起钊，殷金生.理论力学［M］.北京：北京大学出版社，1982

［17］ Phillips W F，Hailey C E，Gebert G A.The effects of orthogonality error in aircraft flight simulation［C］.The 39thAIAA Aerospace Sciences Meeting and Exhibit，Reno，USA，2001

［18］ Phillips W F， Hailey C E.A review of attitude kinematics for aircraft flight simulation［C］.AIAA Modeling and Simulation Tehnologies Conference，Denver，USA，2000

［19］ 程国采.四元数法及其应用［M］.长沙：国防科技大学出版社，1991

［20］ 许毛跃，张登成，李嘉林.四元数在欧拉方程中的应用研究［J］.飞行力学，2002，20（1）：67-70

［21］ 周江华，苗育红，李宏，孙国基.四元数在刚体姿态仿真中的应用研究［J］.飞行力学，2000，18（4）：29-32

［22］ 费景高.捷联式制导系统中四元数的保范递推计算［J］.航天控制，2000，18（3）：37-43

［23］ Blankinship K.A new kinematic theorem for rotational motion［C］.IEEE Position Location and Navigation Symposium，Midwest City，USA，2004

［24］ Bortz J E.A new concept in strapdown inertial navigation［R］.NASA-TR-329，1970

［25］ Bortz J E.A new mathematical formulation for strapdown inertial navigation［J］.IEEE Trans.on Aerospace and Electronic Systems， 1971， 7（1）：61-66

［26］ 张士邈.适合高动态环境的捷联惯导系统高精度算法研究［D］.西北工业大学硕士学位论文，2002

［27］ 林雪原，刘建业，赵伟.一种改进的旋转矢量姿态算法［J］.东南大学学报（自然科学版），2003，33（2）：182-185

［28］ 周江华，王峰，孙国基.多子样旋转矢量捷联姿态算法的一般结果［J］.航天控制，2002，20（2）：18-22

［29］ 牟淑志，卜雄洙，李永新.高动态环境下的捷联惯导系统姿态算法的研究［J］.弹箭与制导学报，2006，26（3）：11-16

［30］ 余杨，张洪钺.捷联惯导系统中的圆锥和伪圆锥运动研究［J］.中国惯性技术学报，2006，14（5）：1-4

［31］ Kim K，Lee T G.Analysis of the two-frequency coning motion with DINS［C］.AIAA Guidance，Navigation and Control Conference and Exhibit， Montreal，Canada，2001

［32］ 武元新.对偶四元数导航算法与非线性高斯滤波研究［D］.国防科学技术大学博士学位论文，2005

On Attitude Quaternion

MA Yanhong1，2，HU Jun1
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

The quaternion calculation for spacecraft attitude determination is investigated in this paper，including the transformation between quaternion and the direction cosine matrix，the quaternion differential equation，the selection of time steps for integrating the quaternion equation，and the compensation methods for the noncommutativity error in high dynamic motion.The dual quaternion is also addressed.

attitude determ ination； direction cosine matrix； quaternion； noncommutativity error；dual quaternion

V448.22

A

1674-1579（2008）03-0055-06

2007-12-10

马艳红（1980-），女，山西人，博士研究生，研究方向为鲁棒控制和航天器交会对接（e-mail：mayanhong1980@sina.com.cn）。