一种航天器智能自适应控制方法*

2008-12-19沈少萍吴宏鑫

空间控制技术与应用 2008年3期

关键词：适应控制挠性刚体

沈少萍，吴宏鑫

（1.北京控制工程研究所，北京100190；2.空间智能控制国防重点实验室，北京100190）

一种航天器智能自适应控制方法*

沈少萍1，2，吴宏鑫1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制国防重点实验室，北京100190）

航天器智能自适应控制是航天器智能自主控制的一个重要组成部分。研究以带可伸缩挠性附件航天器为对象，以实现高精度、高稳定度和强适应性为目标的智能自适应控制的基本原理和方法，根据对象特征模型和自适应黄金分割控制律提出了基于附件长度的变参数主动控制方法，即中心刚体控制与挠性附件主动控制相结合的联合自适应控制方法。数学仿真结果表明不管航天器挠性附件伸展或收缩，亦或是受到共振扰动，该控制器都能快速抑制姿态角和模态的振动，而且姿态角和模态超调量都很小，其控制效果优于其他控制器的控制效果。

集散型智能自适应控制；带可伸缩挠性附件航天器；特征模型

1 引言

所谓“智能自适应控制”就是以自适应控制中自适应控制器和自适应估计器为主，引入专家经验、自学习和人工智能等有关智能控制特征的控制。航天器智能自适应控制是航天器智能自主控制的一个重要组成部分，关于智能自主控制技术，杨嘉墀院士在1995年的论文［1］中就明确提出“对中国来说发展这项技术更有其必要性”，同时在文献［1］还列出了具有挠性结构航天器的控制、自主导航与轨道控制、故障诊断和系统重构以及空间机器人控制等4个具体发展领域。航天控制科技工作者10多年来根据任务需求和航天器的不同特点，对上述领域进行了大量研究，并取得了一定成果。本文将以一类复杂航天器为对象，以实现高精度、高稳定度和强适应性为目标，研究智能自适应控制的基本原理和方法。

2 航天器特点及控制系统的结构

本文所研究的航天器，带有轻质的挠性空间结构。航天器在运行中由于任务要求呈现出变结构变系数（参数）的特点。这些特点使被控对象表现为时变、不确定性、非线性、分布参数、高维多变量及强耦合的动力学特性，精确的数学建模很困难。

对于具有上述结构特点的航天器要实现姿态高精度、高稳定度及强适应性的控制性能，其控制系统根据多年研究结果，拟采用集散结构形式。

一般具有上述结构特点的复杂卫星，由多个子系统组成，各子系统之间既有联系又彼此独立，为阻止一个子系统出现故障影响其他子系统，应尽可能独立控制，然而它又是一个整体，应保持统一管理、控制与操作。最近我们对中心刚体姿态控制、挠性附件指向控制与振动抑制采用集中分散主被动结构控制方法，从仿真结果来看远超过其它结构形式控制的效果。

3 集散型智能自适应控制器设计方法

下面以带可伸缩挠性附件航天器的姿态控制和附件的振动抑制为例，来说明集散型智能自适应控制器的设计方法［2］。

3.1 对象动力学模型

如图1所示，被控对象由中心刚体及其所带的可伸缩挠性附件组成，挠性附件伸展速度为。被控对象的本体坐标系为OX1Y1Z1，其中原点O是刚体的质心，X1轴沿挠性附件方向，Z1轴垂直纸面向外。惯性坐标系为 OX0Y0Z0，其坐标原点与本体坐标系原点重合，且Z0轴与本体坐标系的Z1轴重合，两坐标系之间只相差一个绕Z轴的转角。这里只讨论单轴姿态运动，用角速度ω来描述本体系与惯性系之间的运动学关系。

图1 可伸缩附件末端不带集中质量的航天器示意图

（1）基本假设

假设挠性附件的长度远远大于其宽度和厚度，且线密度均匀，这样就不用考虑转动惯量和剪切变形的影响，只需考虑附件的横向弯曲振动。假设刚体的转动角速度 ω、角加速度 ω·、挠性附件变形、变形速度和变形加速度均为小量，忽略二阶小量。

（2）符号定义

a0：挠性附件在刚体上的安装点到质心 O的位移，在本体坐标系中为［a00 0］T；r：挠性附件上微元到质心O的位移；r1：挠性附件未变形情况下，挠性附件上微元到安装点的位移，在本体坐标系中为［r10 0］T，r1＞0；ω：本体系相对惯性系的角速度，在本体坐标系中为［0 0]T或写为［0 0 ω］T；h：挠性附件在长度方向的线密度，为常值：l（t）：t时刻挠性附件伸展出的长度；：挠性附件伸展速度或收缩速度；EJ：附件的弯曲刚度；L：挠性附件能完全伸展的总长度；Joz：刚性本体绕 Z轴的转动惯量；Ωf：挠性附件实际振动频率对角矩阵；ks：各阶振型的相对阻尼系数（本文考虑挠性附件的自然阻尼并假设各阶振型的相对阻尼系数都相等）。

（3）动力学方程

其中

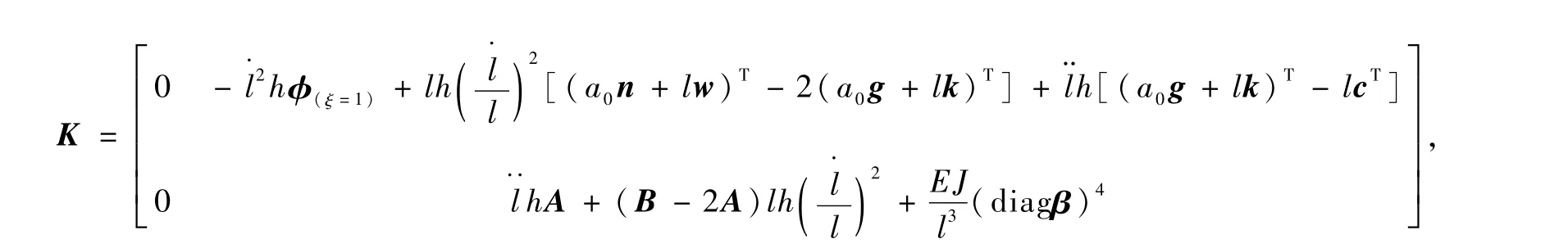
下面给出 φ（ξ）=［φ1（ξ） φ2（ξ） … φn（ξ）］T、φ′ξ（ξ）=［φ′ξ1（ξ） φ′ξ2（ξ） … φ′ξn（ξ）］T和φ″ξξ（ξ）=［φ″ξξ1（ξ） φ″ξξ2（ξ） … φ″ξξn（ξ）］T的计算步骤（φ′ξ和 φ″ξξ（ξ）分别是 φ（ξ）对 ξ的一阶偏导数和二阶偏导数，n为被考虑的挠性模态阶数）：

1）解方程

得到 βi；

2）根据 βi，计算

σi=（coshβi+cosβi）/（sinhβi+sinβi）；3）将 βi，σi代入

得到 φ（ξ）、φ′ξ（ξ）和 φ″ξξ（ξ）。

把系统动力学方程式（1）写成状态方程形式，得

3.2 对象特征模型

根据特征建模的原理［3］，仿照线性时变系统单变量特征模型的推导过程［2］，容易推得式（1）线性时变系统的多变量特征模型

其中，f01，f02，g00，g0i，fi1，fi2，gi0，gij是特征模型参数。

3.3 集散型智能自适应控制器设计

（1）特征模型参数辨识

采用带有遗传因子的最小二乘算法对特征模型式（3）进行参数辨识，当可得到系统的前n^阶模态信息时，式（3）中取 i，j=1，2，…，n^。当 |θ|小于某一数值时，停止参数辨识。

（2）控制器形式

鉴于本系统带可伸缩或固定长度的挠性附件，其伸与缩的长度及速度是统一管理和控制，其姿态与附件振动抑制采用分散控制或复合控制。由于可伸缩挠性附件伸缩到不同的长度系统转动惯量和附件频率都很不一样，因此本文提出了基于附件长度的变参数主动控制方法，即中心刚体控制与挠性附件主动控制相结合的联合自适应控制方案，也称之谓集散型智能自适应方法。

加在中心刚体上的控制器u为带有黄金分割系数的PD自适应控制律；加在挠性附件智能材料上的控制qi结合了自适应黄金分割控制律与微分控制律，引入反馈q，有关对于用智能材料测量q并对附件施加致动量的原理这里就不具体给出，可参考文献［4］。具体控制律如下：

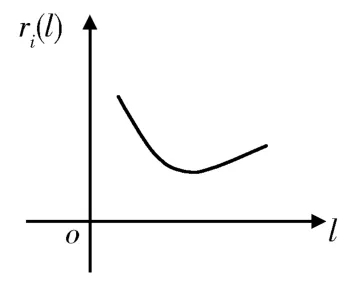
图 2 ri（l）随 l变化的曲线图

图 3 kdi（l）随 l变化的曲线图

4 仿真结果

数学仿真对象为式（2），采用的挠性附件材料为铝，线密度取为 h=1kg/m，抗弯刚度 EJ=23.65N·m2，附件的总长度 l=50m，中心刚体转动惯量 J0z=1000kg·m2，挠性附件在刚体上的安装点到质心的距离a0=2m，采样周期为 0.1s，收缩律取为=（-l/200）m/s，伸展律取为=（32/l2）m/s。设受控对象有四阶模态（n=4），对象模型的具体参数见文献［2］，采用第3节所设计的集散型智能自适应控制器进行控制，控制器仅针对前两阶模态进行设计（=2），并将其控制结果与仅对中心刚体施加控制量的变参数 PD被动控制器［2］控制结果相比较。限于篇幅，本文仅给出姿态角θ和一阶模态q1的数学仿真结果，本文到达稳态的时间是指从某个时刻后θ和q1绝对值分别小于或等于0.001°和0.001m所需的时间。

4.1 系统不受外扰动

（1）附件从50m收缩到20m

智能自适应控制器控制结果如图4所示，θ超调量为0.048°，q1超调量0.0025m，到达稳态时间104s。变参数PD被动控制器控制结果如图5所示，θ超调量为 -0.356°，q1超调量0.312m，到达稳态时间 1100s。

（2）附件从20m伸展到50m

智能自适应控制器控制结果如图6所示，θ超调量为0.0072°，q1超调量0.0012m，到达稳态时间51s。变参数PD被动控制器控制结果如图7所示，θ超调量为0.0625°，q1超调量0.0275m，到达稳态时间1500s。

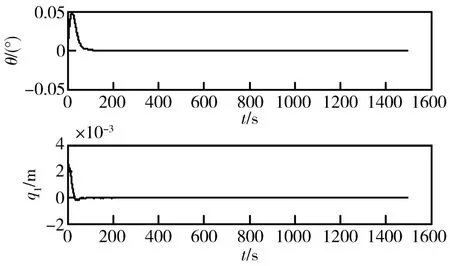
图4 智能自适应控制器的控制结果（从50m到20m）

4.2 姿态控制器开启，系统受到共振扰动

附件从50m收缩到10m，设收缩过程系统各阶模态都受到外扰动：

其中，0.0427rad/s是附件长度为50m左右时的二阶频率及收缩到20m左右（收缩183s）时的一阶频率；0.1712rad/s是附件收缩到长度为41.74m左右（收缩36.2s）时的三阶频率、长度 25m左右（收缩138.7s）时的二阶频率和长度10m（收缩322s）时的一阶频率。收缩过程附件会发生瞬时共振的延续和加强现象［2］，收缩结束后发生持续共振现象。

图5 变参数PD被动控制器的控制结果（从50m到20m）

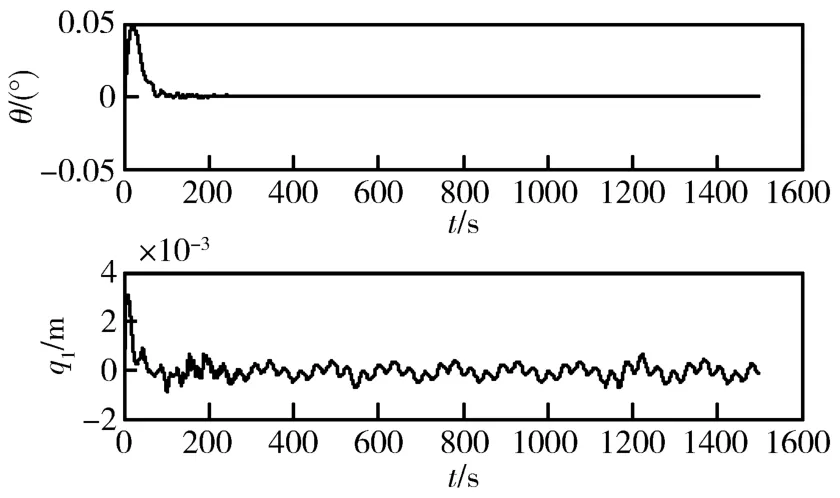
图6 智能自适应控制器的控制结果（从20m到50m）

图7 变参数PD被动控制器的控制结果（从20m到50m）

智能自适应控制器控制结果如图8所示，共振得到了有效的抑制，θ稳态误差为 ±（5×10-5）o，q1稳态误差为±6×10-4m。变参数PD被动控制器控制结果如图9所示，从图可看出共振虽被抑制了，但抑制程度不强，稳态时 θ误差为 ±0.05°，q1稳态误差为±0.1m。

以上仿真结果表明不管航天器挠性附件伸展或收缩，亦或是受到共振扰动，用本文所设计的集散型智能自适应控制器都能快速地抑制姿态角和模态的振动，而且姿态角和模态超调量都较小，其控制效果远远优于变参数PD被动控制器的控制效果，从文献［2］可知，本文给出的方法其控制性能和基于确知系统模型设计的最优主动控制器控制性能相当。

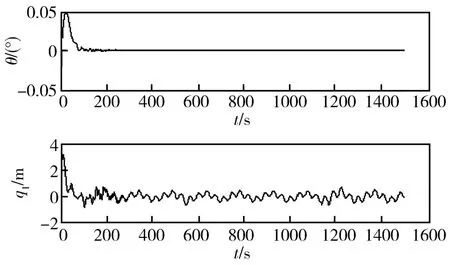
图8 智能自适应控制器抑制共振的仿真结果

图9 变参数PD被动控制器抑制共振的仿真结果

5 结论

本文介绍了一种集散型智能自适应控制方法，从仿真结果看本方法均优于文献［2］中设计的其他控制方法。鉴于篇幅限制，对其他控制方法的控制结果可参见文献［2］，至于实际工程系统的技术实现，本文就不做详细叙述。

［1］ Yang JC.Development of intelligent autonomous control technology for Chinese space program［C］.IFAC International Conference on Intelligent Autonomous Control in Aerospace，Beijing，China，August，1995

［2］沈少萍.带可伸缩挠性附件航天器的姿态控制及附件的振动抑制［D］.中国空间技术研究院博士学位论文，2007：77-86

［3］吴宏鑫，刘一武，刘忠汉，解永春.特征建模与挠性结构的控制［J］.中国科学（E辑），2001，31（2）：137-149

［4］孙东昌.压电智能梁振动控制中致动片优化配置与实验［J］.中国空间科学技术，1999，12（6）：46-52

A Method of Intelligent Adap tive Control for Spacecraft

SHEN Shaoping1，2，WU Hongxin1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

Intelligent adaptive control of spacecraft is an important part of intelligent autonomous control for spacecraft.In this paper，by taking the spacecraft with dep loyable and retractable flexible appendage as the object，the principle and method of intelligent adaptive control are researched so as to realize the control target of high precision，high stability and strong adaptability.According to the characteristic model and the golden section adaptive control law，a parameter varying active adaptive control method based on the length of the flexible appendage is presented.This method combines the control of center rigid body with the active control of appendage.Numerical simulations show that by applying the parameter varying active adaptive control，the vibration of the attitude angle and modes can be rapid ly suppressed and the overshoots are very small when the appendage deploys，retracts or is excited by resonance disturbances and that the designed controller excels other controllers.

collecting and distributing intelligent adaptive control； spacecraft with deployable and retractable flexible appendage；characteristic model