基于紫外敏感器和星敏感器的卫星自主导航

管乐鑫，魏春岭

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190）

基于紫外敏感器和星敏感器的卫星自主导航

管乐鑫1，2，魏春岭1，2

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190）

卫星利用紫外敏感器和星敏感器进行自主导航的方法中地心矢量的测量精度是影响导航精度的重要因素之一，而地心矢量的测量又受到地球扁率的影响。在考虑地球扁率的前提下，研究了地球扁率对地心矢量测量的影响，给出了基于卫星姿态的地心矢量的补偿方法。仿真结果表明该补偿方法具有较高的补偿精度，并且能有效地提高卫星自主导航精度。

自主导航；地心矢量；地球扁率；卫星姿态

1 引 言

航天器自主导航是指航天器在不依赖地面支持的情况下，通过其自身所携带的测量设备确定航天器的位置和速度。对于卫星系统来讲，自主导航有利于降低卫星对地面的依赖程度，提高系统的生存能力。

地球的形状并不是标准的球体，可近似为绕极轴的旋转椭球。地球紫外辐射带的形状也可以描述为与椭球形地球相似、具有相同中心的旋转椭球。目前，由地球扁率引起的航天器轨道摄动的计算已达到相当高的精度，由模型误差引起的估计偏差可以控制得很小。但是在敏感器测量过程中，通常认为地球为标准圆球，常常忽略地球扁率对敏感器测量的影响。文献［1］和［2］都是以理想圆球作为地球模型。文献［3］在以扫描式红外地球敏感器为测量设备的前提下，考虑了地球扁率对测量数据的影响，没有涉及地球扁率对成像型敏感器测量数据的影响。本文在已知标称轨道下研究地球扁率对紫外敏感器地心矢量测量的影响，提出相应的补偿方法，再以补偿后的数据作为卡尔曼滤波的观测值。

2 扁率的影响

紫外敏感器具有30°的圆锥形中心视场，和一个120°～160°的环形视场。在紫外波段，紫外敏感器能探测出整个地球边缘的图像，利用大量边缘点信息拟合成像的几何中心，从而获得地心矢量的测量数据。

首先定义坐标系和标称轨道：

1）赤道惯性坐标系：原点在地心，Xi轴沿赤道面与黄道面的交线，指向春分点；地球的自旋轴为Zi；Yi轴和 Xi、Zi轴构成右手正交坐标系。

2）质心轨道坐标系：原点在卫星的质心上，Zo轴由质心指向地心；Xo轴与Zo轴在轨道平面内垂直，指向卫星速度方向；Yo轴与 Xo、Zo轴构成右手正交坐标系，与轨道平面的法线平行。

3）紫外敏感器测量坐标系：原点位于理想的光学透镜的中心，Zs轴沿敏感器光轴方向；Xs轴垂直于光轴并与CCD行扫描方向一致；Ys轴与 CCD列扫描方向一致，与Xs轴、Zs轴构成右手坐标系。对于三轴稳定卫星，假设Zs轴指向近天体，Xs轴沿卫星速度方向。

4）卫星飞行高度约500 km的圆轨道，标称轨道参数取为

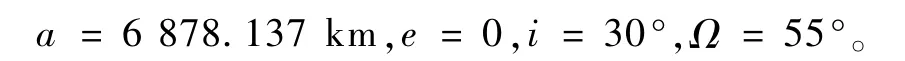
将地球紫外辐射带的形状描述为绕地球极轴形成的旋转椭球，其表面E在地心赤道惯性系中的方程为

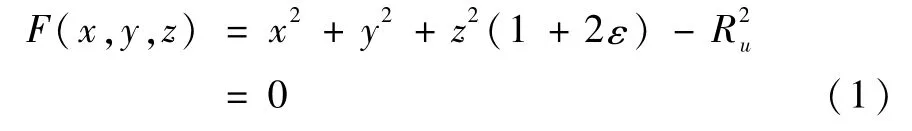
其中，ε为地球扁率，Ru为地球紫外辐射椭球在赤道的半径。

设卫星S在赤道惯性系下的坐标为（u，v，w），从S向地球引切线矢量=，与曲面 E相切于 P（x，y，z）点，与 P点处的曲面法线矢量 →n正交，根据此条件导出地平平面方程

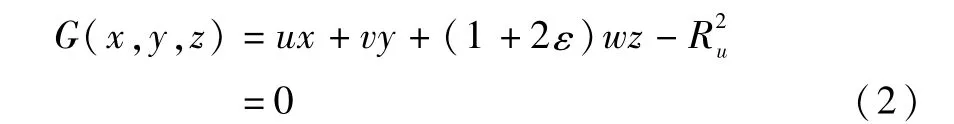
因此地球轮廓线方程为

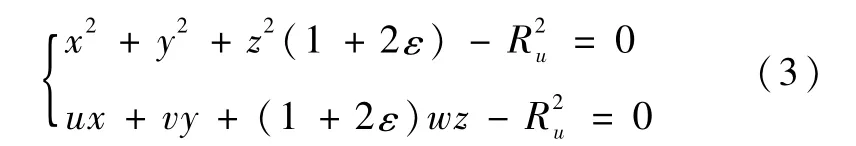
由此就可以确定地球边缘点在赤道惯性坐标系下的坐标，通过公式

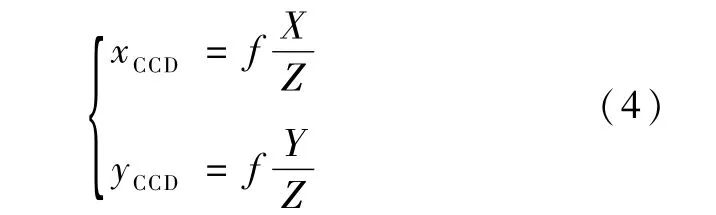
就可以确定边缘点在CCD平面中像点的坐标（xCCD，yCCD）（此时的（X，Y，Z）为地球边缘点在测量坐标系下的坐标），利用边缘拟合算法求出几何中心，通过

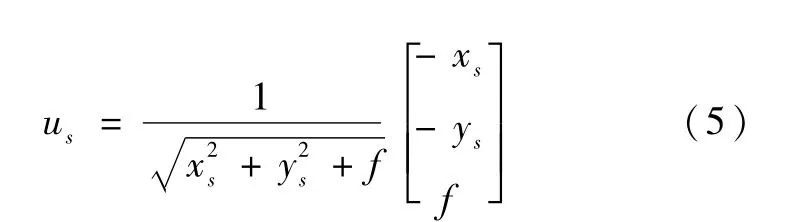
就可以求出地心矢量在测量坐标系下的表达（（xs，ys）为几何中心的坐标，f为焦距）。

以往的研究往往忽略地球扁率，以标准球体作为地球模型，以标准圆或标准椭圆作为边缘拟合的模型，并且认为拟合后的几何中心就是地球中心在CCD平面的像点，并利用此点计算地心矢量在测量坐标系的表达。

当考虑地球扁率时，地球成像更加复杂，通过对成像的研究发现：1）地球成像并不是简单的二次曲线，而是复杂的高次曲线，但是可以近似看成二次曲线；2）当考虑卫星姿态时，地球成像不仅旋转而且平移。所以为了提高拟合精度，选取拟合模型为［4］

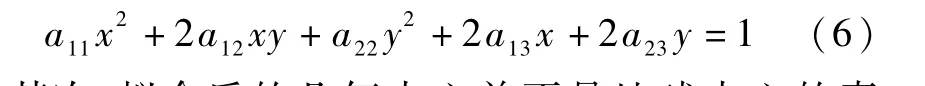
其次，拟合后的几何中心并不是地球中心的真实像点。图1中（a）、（b）为滚动角和俯仰角都为0°时，两点的坐标误差示意图；（c）、（d）为滚动角为1°、俯仰角为1.5°时，两点间的坐标误差示意图（偏航角对地球成像没有影响，所以假定偏航角为0°）。

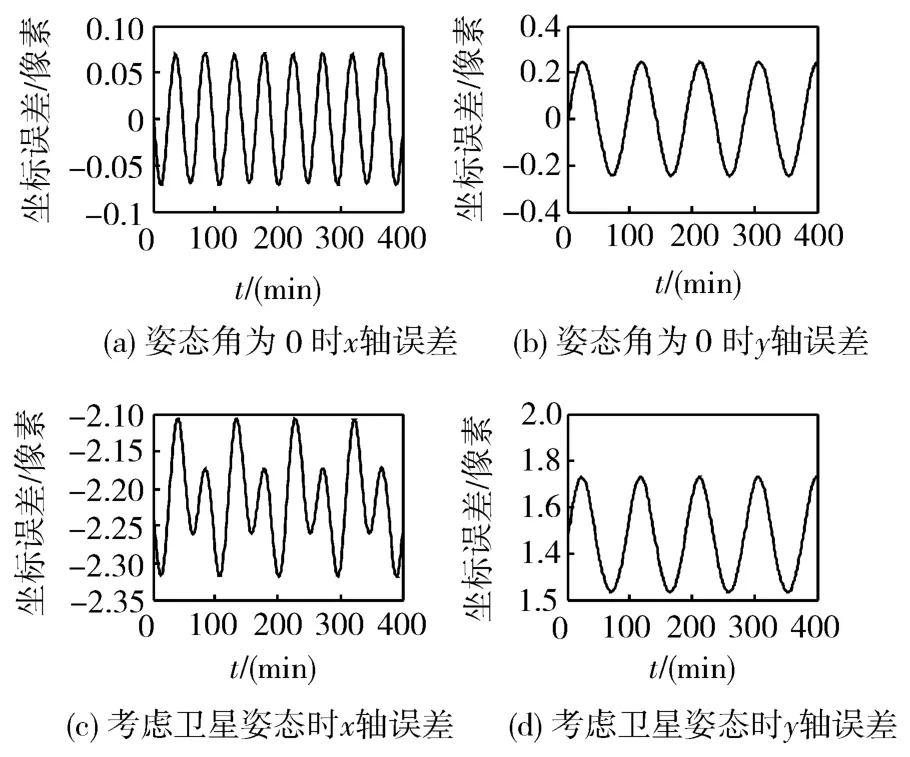
图1 CCD平面坐标系坐标误差示意图

所以直接利用拟合后的几何中心计算出的矢量与真实的地心矢量必定不重合。

通过上面的仿真可见，地球扁率对地心矢量的测量是有影响的，并且随着姿态角的增大而增大，所以就需要对其进行补偿。

3 测量数据的补偿

由图1可见，地球扁率对地心矢量的测量有影响，并且这种影响是有规律的，有补偿的可能性。

3.1 补偿原理

通过式（5）已经得到地心测量矢量 us，令真实地心矢量为 ue。把 us和 ue的夹角进行分解，分解成滚动误差角φm和俯仰误差角θm（如图2，实线表示理想观测图形，虚线表示实际观测图形，（xs，ys）为拟合几何中心，（xe，ye）为真实地心成像点）

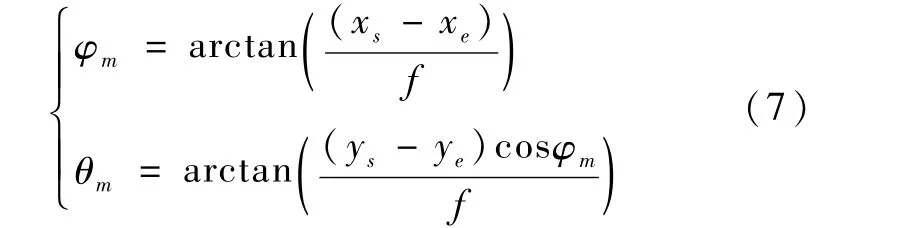
图3中，（a）为滚动角和俯仰角都为0°时，φm和 θm的示意图；（b）为滚动角为 1°、俯仰角为 1.5°时，φm和θm的示意图。

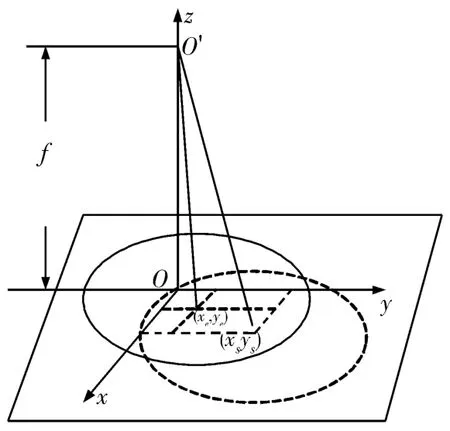
图2 紫外图像几何关系图

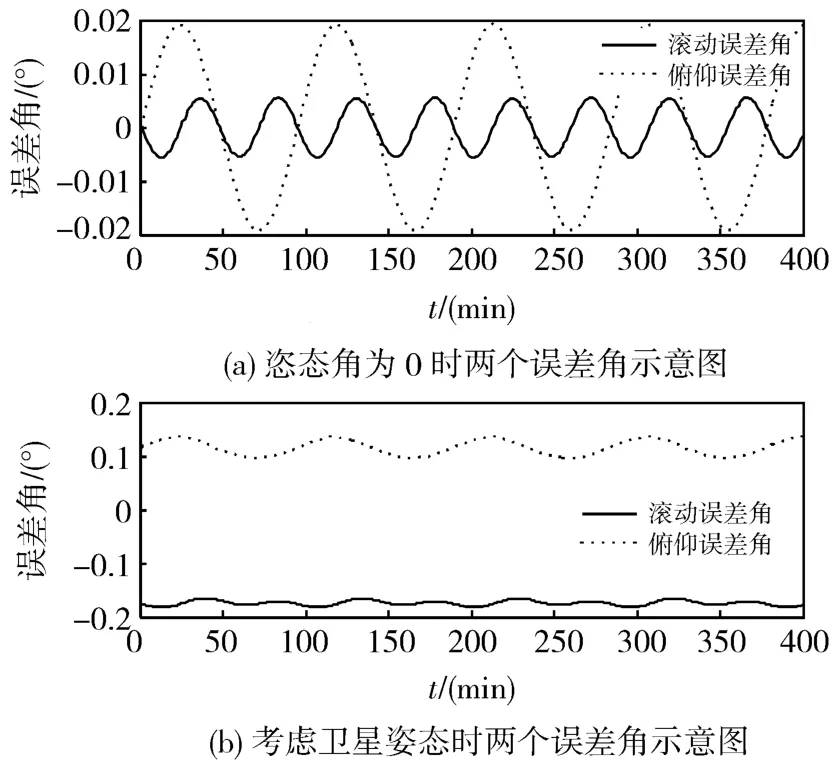
图3 φm和θm示意图

由图3可知，φm和 θm的变化近似为简单的三角函数，所以考虑利用三角函数对两个角进行近似。令近似函数为

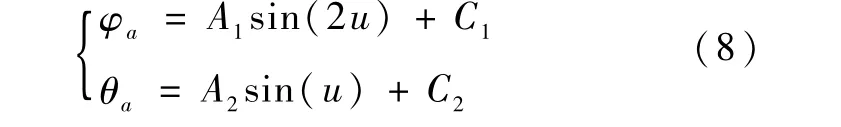
其中，u为近地点幅角与真近点角之和。

通过仿真发现，A1、A2和 C1、C2随滚动角和俯仰角的变化而变化。所以首先以俯仰角为变量，利用拉格朗日插值方法求出、和，然后以滚动角为变量，利用拉格朗日插值方法求出和、。把两组数值按照式（9）计算，就可以求出A1、A2和 C1、C2。系数是通过大量仿真、反复比对和不断调整确定的。

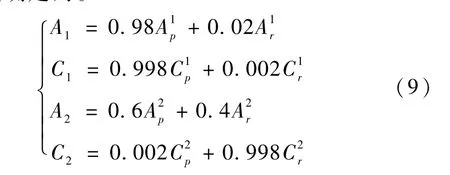
获得 φa和 θa后，就可以求出（xe，ye）

3.2 仿真验证

图4为当滚动角和俯仰角都为0°时，两个误差角的近似示意图及近似误差图（在近似图中，虚线为真实曲线，实线为近似曲线）。

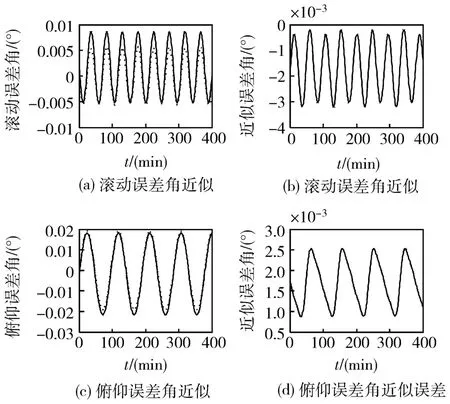
图4 φm和θm近似示意和误差图

图5为补差前与补偿后几何中心与地心真实像点间的坐标误差比较图。

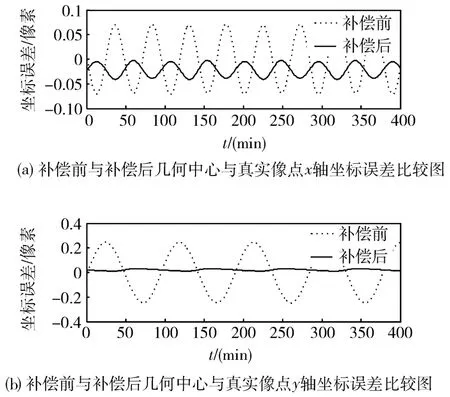
图5 坐标误差比较图

图6为当滚动角为1°、俯仰角为1.5°时，两个误差角的近似示意图及近似误差图（在近似图中，虚线为真实曲线，实线为近似曲线）。

图7为补差前与补偿后几何中心与地心真实像点间的坐标误差比较图。

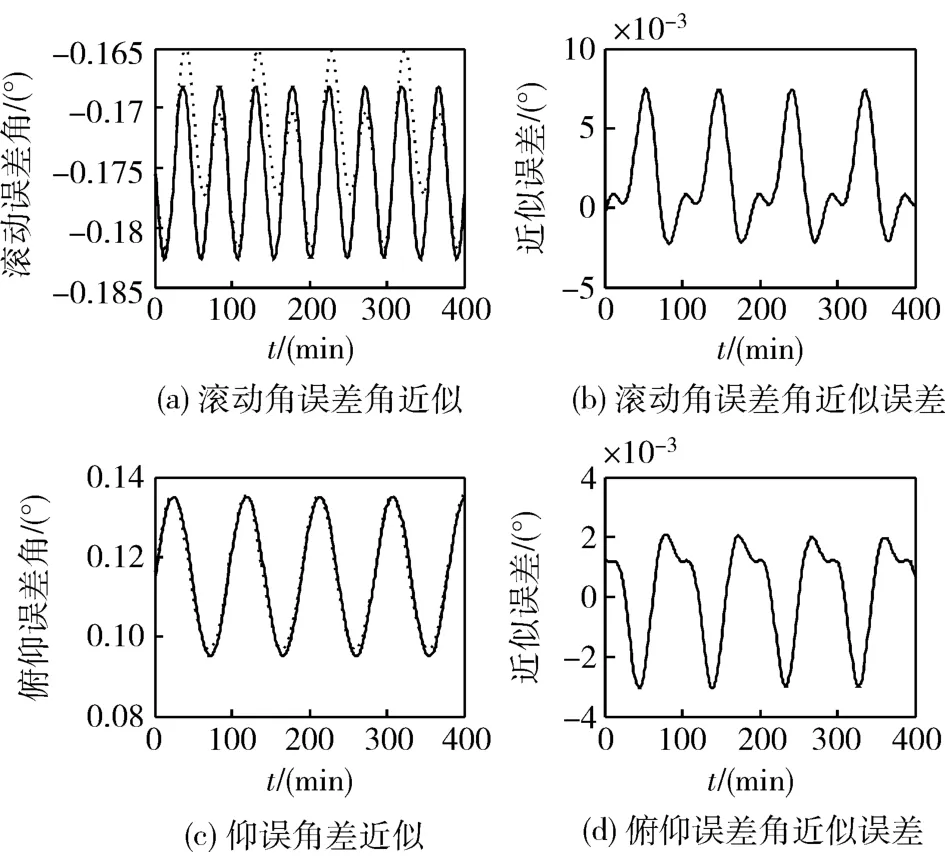
图6 φm和θm近似示意图和误差图

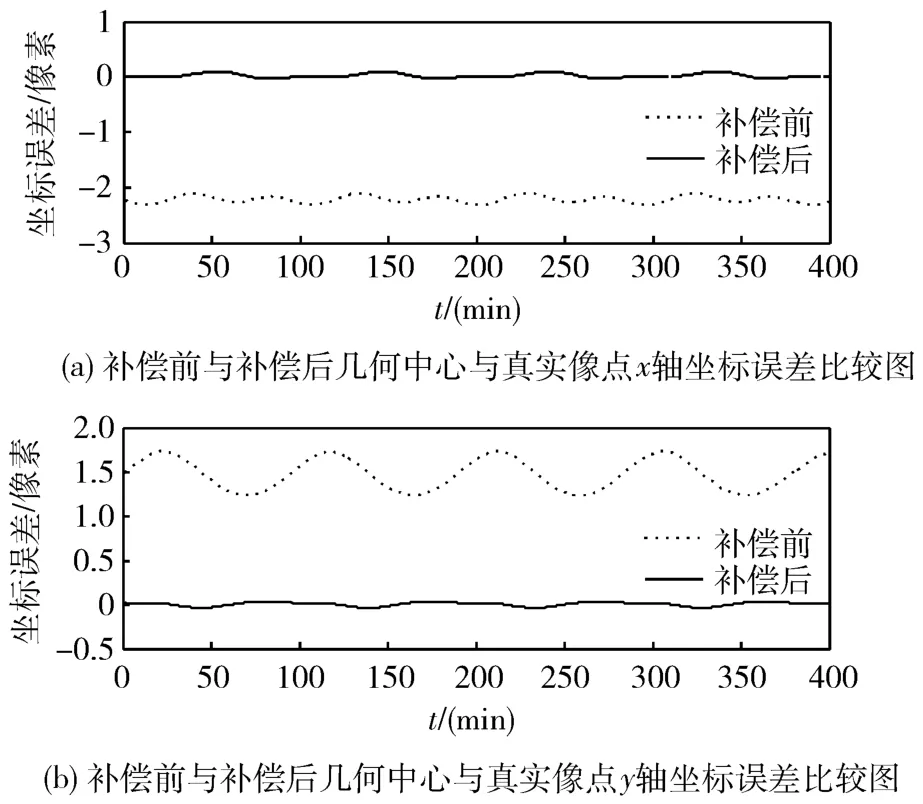
图7 补偿坐标误差比较图

通过以上仿真可见，经过补偿后，几何中心与真实地心像点的坐标误差明显减小，说明了此补偿方法的有效性。

4 滤 波

4.1 卡尔曼滤波

卫星轨道动力学可由如下微分方程描述［5］

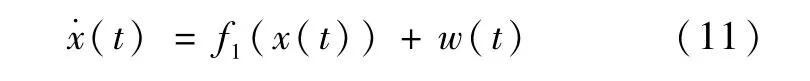
其中，x为状态变量，其6个元素由地心赤道惯性坐标系中的3个位置分量和3个速度分量组成（暂不考虑大气阻力系数校正）；w（t）为各摄动项的建模误差。

卫星轨道动力学模型中除中心引力项外，仅考虑J2项摄动，其分量形式为

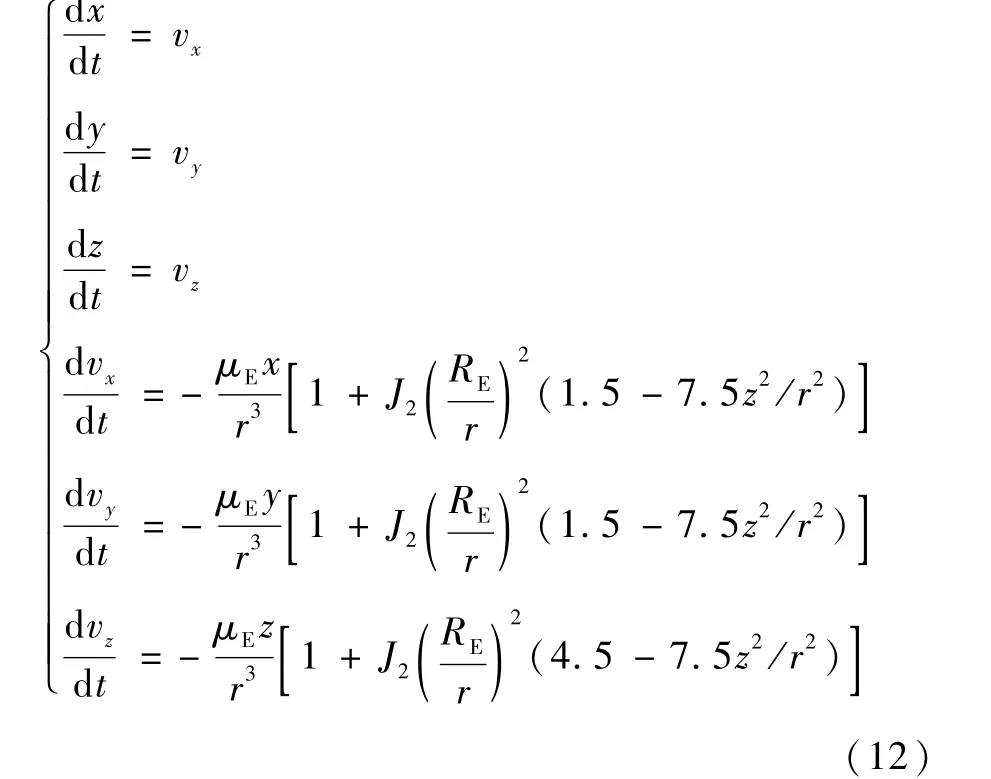
观测量为地心方向矢量和地心距，离散形式的测量方程可以写成

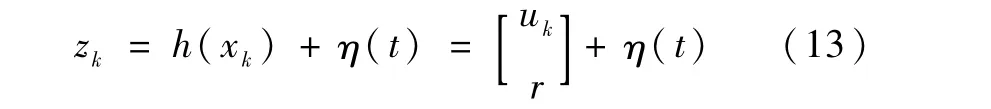
其中，η（t）为观测噪声。

在仿真中取：

1）仿真程序通过龙格库塔法获得轨道数据，在龙格库塔法中，卫星轨道动力学模型除地球的中心引力项外，还包括高阶引力项J2，J3和 J4，而导航滤波器的轨道预报模型除地球的中心引力项外只包括J2项。

2）地心方向在惯性系三轴分量的测量噪声均方差均取为0.02°。

3）在导航坐标系（地心惯性坐标系）中位置矢量的3个分量和速度矢量的3个分量的初始误差分别为5 000 m和30 m/s；仿真时间为20 000 s，统计最后的5 000 s。

4）导航精度定义为

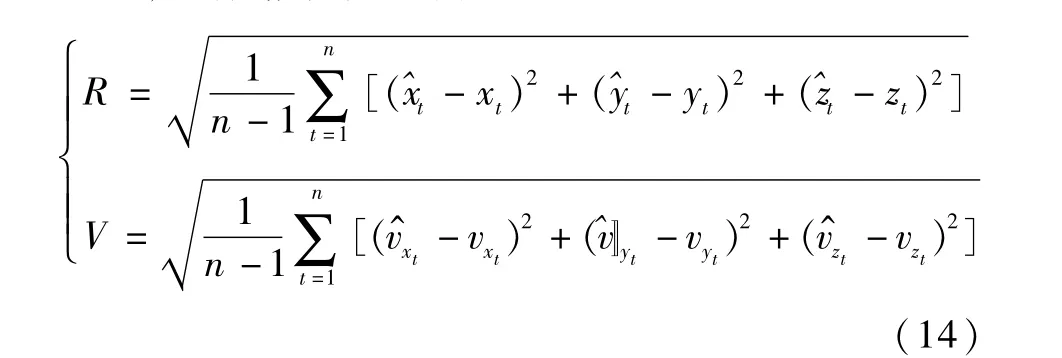
5）滤波误差图中位置误差和速度误差定义为

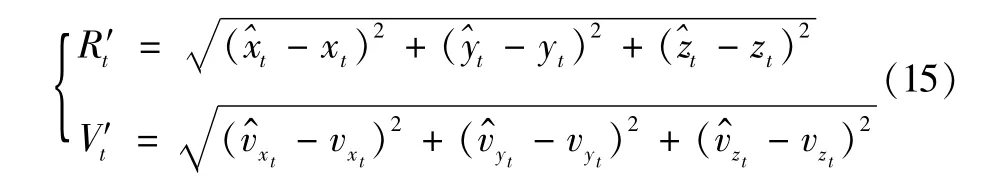
其中，R′t和 V′t为 t时刻的位置误差和速度误差，t=1，2，…，20000。

4.2 仿真验证

图8为当滚动角和俯仰角都为0°时，补偿前与补偿后滤波误差比较图：

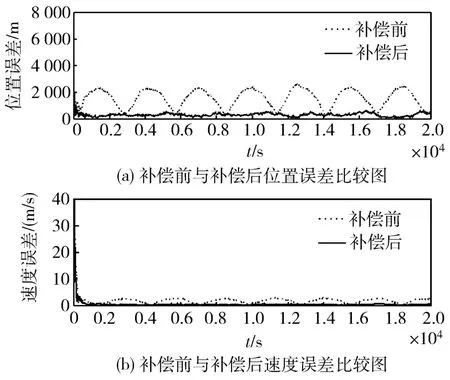
图8 补偿前与补偿后滤波误差比较图

补偿前导航精度为：

位置精度：1 701.617 m；速度精度：1.821m/s。

补偿后导航精度为：

位置精度：339.108 m；速度精度：0.386 m/s。

图9为当滚动角为1°、俯仰角为1.5°时，补偿前与补偿后滤波误差比较图。

补偿前导航精度为：

位置精度：23 195.525 m；速度精度：25.079 m/s。

补偿后导航精度为：

位置精度：351.843 m；速度精度：0.439 m/s。

通过上面的仿真可见，经过补偿后，滤波精度得到较大提高，由此说明了此补偿方法的有效性。

Satellites Autonom ous Navigation Based on U ltraviolet Sensors and Star Sensors

GUAN Yuexin，WEIChunling
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

An autonomous orbit determination method based on ultraviolet sensors and star sensors is presented.The accuracy of the measurements of the geocentric vector plays a key role in satellite navigation，but it is affected by the earth oblateness.With the earth oblateness taken into account，simulations are used todetermine the effect of the earth oblateness on the geocentric vector，and a compensation process based on satellite attitudes is proposed.The results show that the compensation process has high accuracy and canimprove navigation accuracy effectively.

2008-02-15

管乐鑫（1982-），男，吉林人，硕士研究生，研究方向为卫星自主导航（e-mail：davaid19820526@163.com）。

autonomous navigation； geocentric vector；earth oblateness；satellite attitude

V448

A

1674-1579（2008）03-0037-05