三角形角平分线应用例析

刘玉东

三角形的角平分线是三角形的主要线段之一.它在几何的计算或证明中，起着“桥梁”的作用．那么，如何利用三角形的角平分线解题呢？下面举例说明．

一、“以角平分线为轴翻折”构造全等三角形

此情形下可构造两种基本图形，如图1、图2所示.

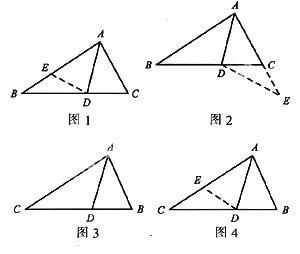
△ABC中，AD是角平分线.如图1，以AD为轴翻折，使点C落在AB上（即在AB上截取AE=AC），得△ACD≌△AED．如图2，以AD为轴翻折，使点B落在AC的延长线上（即延长AC到E，使 AE=AB），得△ABD≌△AED．

例1如图3，在△ABC中，AD平分∠BAC，且AB+BD=AC.求∠B ∶∠C的值．

解法1：如图4，在AC上截取AE=AB，连接DE．

则△ABD≌△AED（SAS）.

∴∠B=∠AED，BD=ED．

又∵AB+BD=AC，

∴CE=BD=ED.

∴∠C=∠EDC.

∴∠B=∠AED=2∠C.

∴∠B∶∠C=2∶1．

解法2：延长AB到E，使AE=AC ，连接DE．请读者一试．

二、“角平分线+垂线”构造全等三角形或等腰三角形

1. 根据角平分线的性质，自角平分线上任一点向角的两边作垂线，得两个全等的直角三角形.

2. 自角的一边上的一点作角平分线的垂线并延长，与另一边相交，则截得一个等腰三角形．

例2如图5，在四边形ABCD中，BC>BA，AD=CD，BD平分∠ABC．

求证：∠A+∠C=180°．

证明：过点D作DE⊥AB，交BA延长线于点E；作DF⊥BC，交BC于点F ．如图6.

∵BD平分∠ABC，

∴DE=DF ．

又∵AD=CD，

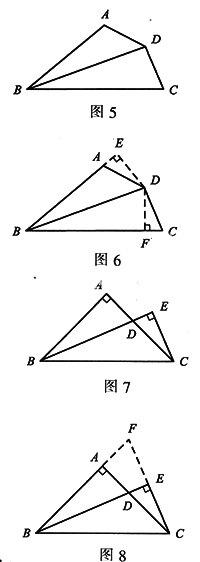
∴Rt△EAD≌Rt△FCD（HL）.

∴∠C=∠EAD．

∵∠EAD+∠BAD=180°，

∴∠C+∠BAD=180°．结论得证.

评注：本题也可通过“以角平分线为轴翻折”的思路解：沿BD翻折△BDC得△BDC′，则△ADC′是等腰三角形，∠C=∠C′=∠EAD.

例3如图7，等腰Rt△ABC中，∠A=90°.∠B的平分线交AC于D，过C作BD的垂线交BD的延长线于E．求证：BD=2CE .

证明：如图8，延长CE交BA的延长线于点F.

∵BE是∠B的平分线，BE⊥CF，

∴∠BCF=∠F.

∴△FBC是等腰三角形．

∴CE=FE．

∴CF=2CE．

∵AB=AC，∠ABD=∠ACF（因在△BAD与△CED中已有两角相等），∠BAD=∠CAF=90°，

∴Rt△BAD≌Rt△CAF．

∴BD=CF=2CE．

评注：上面证法是构造出2CE，也可构造出1/2BD来证：自D作DF∥BC交AB于F.易知△AFD是等腰三角形，AF=AD，故FB=DC.易知△BDF是等腰三角形，FD=FB=DC.作FG⊥BD于G，则DG=1/2BD.由∠CDE=∠BDA=90°-∠ABD，∠DFG=∠BFG=90°-∠ABD，易证△DFG≌△CDE（AAS）.

三、“角平分线+平行线”构造等腰三角形

1. 自角平分线上任一点作角的一边的平行线与另一边相交，得等腰三角形.

2. 自角的一边上任一点作角平分线的平行线与另一边的延长线相交，得等腰三角形．

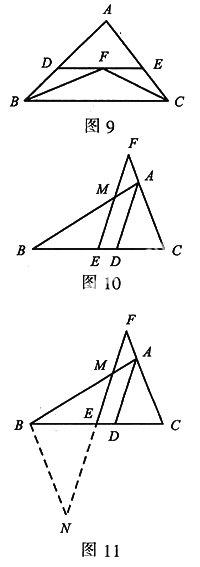
例4如图9，在△ABC中，∠B和∠C的平分线相交于点F.过F作DE∥BC，交AB于D，交AC于E．若BD+EC=9，则线段DE的长为（）.

A. 9B. 8C. 7D. 6

解：∵DE∥BC，

∴∠DFB=∠FBC ．

∵∠FBC=∠FBD，

∴∠DFB=∠FBD.

∴DF=DB．

同理可证EF=EC ．

∵DF+EF=DE，

∴BD+EC=DE，则DE=9. 故应选A.

例5如图10，△ABC中，AD是∠BAC的平分线.E是BC中点.EF∥AD，交AB于M，交CA的延长线于F.求证：BM = CF．

证明：作BN∥FC交FE的延长线于N．如图11.

∵E是BC中点，

∴△BEN≌△CEF（ASA）.

∴CF=BN.

易知△AFM为等腰三角形，从而△BMN也为等腰三角形（∠BNM=∠MFA=∠FMA=∠BMN），BM=BN.

∴BM = CF．

总之，涉及三角形角平分线问题的辅助线的添加，一般不外乎以上三种情形.只要根据题目所给的条件，灵活选用上述三种构造方法，问题一般不难获得解决．