和全等三角形有关的和差式的证明

作者简介 郑俊哲，中国数学奥林匹克一级教练，硕士，1995年毕业于山东曲阜师范大学，中学数学一级教师.所辅导的学生在全国初中数学竞赛中多次获得一等奖，本人也多次被评为“全国数学竞赛优秀辅导员”.制作的多媒体课件多次在山东省课件评比中获得一等奖.

全等三角形是证明线段相等、角相等的一个重要工具.随着学习的深入，出现了证明一些线段的和（差）等于某条线段的题目，让学生感到困难.这时，通过恰当添加辅助线，将线段的和差问题转化为线段的相等问题，同时构造全等三角形，成为解决问题的主要手段.

一、与三角形、四边形有关的线段和差问题

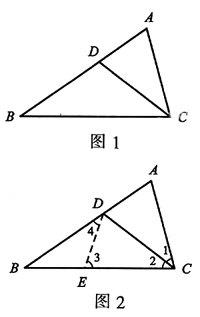
例1如图1，△ABC中，∠A=2∠B，CD平分∠ACB.

求证：BC=AD+AC.

思路1：（截长）在BC上截取CE=CA，连接DE.如图2.

易证△ACD≌△ECD（SAS）.

∴∠3=∠A=2∠B.

∵∠3=∠B+∠4，

∴∠B=∠4.

∴BE=DE=AD.

∴BC=BE+EC=AD+AC.

思路2：（补短）延长CA到E，使得EC=BC，连接DE.如图3.

由条件推出△CED≌△CBD（SAS）.

与思路1相仿，由∠E=∠B，∠BAC=2∠B，得∠4=∠E.AE=AD.下略.

点评：对于线段之间的和差关系，常采用“截长”、“补短”等添加辅助线方法，构造全等三角形，从而转化为两线段间的相等关系.

例2如图4，△ABC中，∠B=2∠C，AD垂直BC于D.

求证：CD=AB+BD.

思路：如图5，在DC上截取DE=DB，连接AE.

易知△ABD≌△AED（SAS）.

∴AB=AE，∠2=∠B.

又∠B=2∠C，得∠1=∠C，AE=CE.

∴CD=CE+DE=AE+DE=AB+DE=AB+BD.

点评：本解法是截长的方法.也可用补短的方法去证：延长DB到E，使BE=BA，连接AE.读者不妨自己试试.

例3如图6，等边△ABC中，延长BA到D，延长BC到E.若DC=DE，求证：AD=AC+CE.

思路：如图7，延长BC到F，使EF=BC，连接DF.因EF=BC=AC，故只要证CF=AD即可.

易证△DCB≌△DEF（SAS）.

∠F=∠B=60°.

故△DBF是等边三角形.

∴BD=BF.

而BA=BC，故AD=CF=CE+EF=CE+AC.证毕.

点评：本题还可以作以下辅助线证明：作EM∥AC交BD于M.证明△ACD≌△MDE（AAS）.

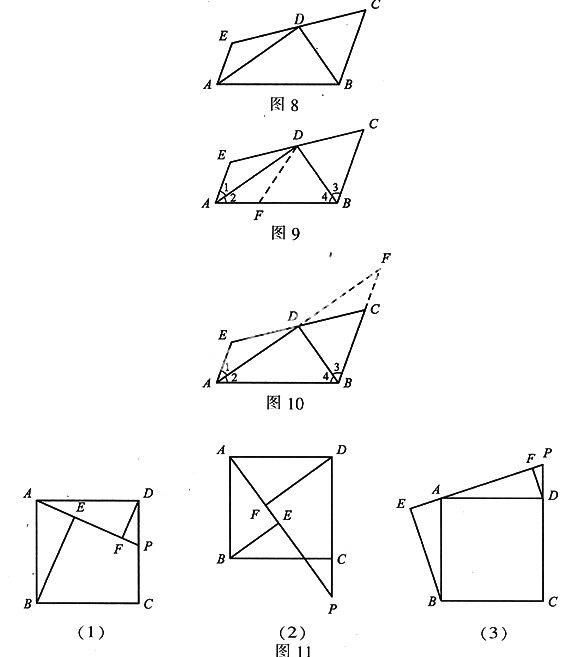
例4如图8，AE∥BC，AD、BD分别是∠EAB、∠CBA的平分线.过点D的直线EC交AE于点E，交BC于点C.求证：AE+BC=AB.

思路1：（截长）在AB上截取AF，使AF=AE，连接DF.如图9.

易证△ADE≌△ADF（SAS）.

∴∠E=∠AFD.

∵AE∥BC，

∴∠E+∠C=180°.

又∵∠AFD+∠BFD=180°，

∴∠C=∠BFD.

∴△BDF≌△BDC（AAS）.

∴BF=BC.AE+BC=AF+BF=AB.

思路2：（补短）如图10，延长BC交AD的延长线于F.要证AE+BC=AB，只需要证明AB=BF和AE=CF.

由题设∠1=∠F=∠2，△ABF是等腰三角形.

∴AB=BF.

又BD是∠FBA的平分线，由等腰三角形“三线合一”知AD=FD.

∴△ADE≌△FDC（ASA）.AE=CF.

∴AE+BC=CF+BC=BF=AB.

二、运动型线段和差问题

例5如图11（1），在正方形ABCD中，点P是CD上一动点，连接PA.分别过点B、D作BE⊥PA，DF⊥PA，垂足分别为E、F.

（1）请探索BE、DF、EF这三条线段长度具有怎样的数量关系，并说明理由.

（2）若点P在DC的延长线上（如图11（2）），那么这三条线段的长度之间又具有怎样的数量关系？请说明理由.

（3）若点P在CD的延长线上（如图11（3）），那么这三条线段的长度之间又具有怎样的数量关系？请说明理由.

简解：（1）结论是：BE-DF=EF.

注意同角的余角相等，易证△ABE≌△DAF（AAS）.

所以EF=AF-AE=BE-DF.

（2）结论是：DF-BE=EF.

与（1）类似，易证△ABE≌△DAF（AAS）.

所以EF=AE-AF=DF-BE.

（3）结论是：DF+BE=EF.理由略，请读者自行探究.

点评：本题是典型的运动型线段和差问题.在运动过程中，图中某些线段保持相似或相同的数量关系.本题的证明中应用三角形全等的性质，“化解”了线段间的和差关系.一般来说，这类题目的证法基本相同或类似.但在个别情况下，线段间不保持原有的关系.

练习

1. 如图12，在△ABC中，AB=AC，∠A=108°，∠1=∠2.求证：AC+CD=BC.

提示：在CB上截取CE=CD，连接DE.证明△ABD≌△EBD（AAS）.

2. 如图13，△ABC中，AD为∠BAC的平分线.M为BC的中点，ME∥AD交BA的延长线于E，交AC于F.求证：CF=BE，AB+AC=2BE.

提示：延长EM到G，MG=FM，连接BG，证△BMG≌△CMF.

3. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

（1）当直线MN绕点C旋转到图14（1）的位置时，求证：DE=AD+BE.

（2）当直线MN绕点C旋转到图14（2）的位置时，求证：DE=AD-BE.

（3）当直线MN绕点C旋转到图14（3）的位置时，试问：线段DE，AD，BE具有怎样的关系？请加以证明.