流体中弹性板声辐射阻尼研究

1 引 言

结构振动声辐射是航空航天、舰船等国防领域的重要研究课题[1]。现代舰船多是由钢质加筋结构组合成的复杂结构[2],船上各种动力设备在舰船航行时,不可避免地发生振动和噪声。噪声通过舰船结构传递的现象常称作“结构噪声”。结构噪声辐射到空气中转化为空气噪声；辐射到水中就形成水下噪声[3]。这些噪声不仅使舰船适居性变坏，而且还影响舰船的隐蔽性。

阻尼是振动系统主要特征，对结构的振动与声辐射有重要的影响。很多学者试图通过对阻尼的研究与探索来改良工程中的振动与噪声问题。徐雪英[4]介绍了振动阻尼机理、阻尼结构以及阻尼应用设计，对振动阻尼技术及其应用作了较为详细的论述。许士桐研究了舰船阻尼措施以及结构中阻尼处理的特点，概述阻尼技术在国内外舰船上的应用。伏同先探讨了阻尼技术以及在舰船减振降噪中的应用。

早期的声辐射主要是从板架结构在超音速与亚音速流动环境中发展起来的。Muhlstein[5]对超音速流动中面板声辐射阻尼提出了实验测量方法。Lyle和Dowell[6-7]对亚音速流动中矩形板的声辐射阻尼与结构阻尼进行了比较研究。随后声辐射阻尼研究扩展到无流动状态下，Wallace[8]给出了有限形状矩形板模型的声辐射阻尼，并研究了激励频率在低于、高于和等于板的临界频率等不同条件下的声辐射阻尼情况。Kriegsmann和Scandrett[9]从结构与声耦合的角度对声辐射阻尼进行了估算。板式结构声辐射阻尼在国内的研究还比较少，郭新毅[10,11]对含损伤结构振动的声辐射阻尼问题进行了探讨。

针对无限障板中弹性板，本文从能量角度，定义声辐射阻尼为振动一周内系统以声波辐射的形式,耗散能量与系统总能量之比值，并推导出声辐射阻尼的计算表达式。首先，计算在流体中弹性板流固耦合面上的法向振动响应，基于Reyleigh积分关系得到相应的辐射面的声压，继而依据本文提出的方法对声辐射阻尼进行了数值模拟，比较了空气中与水中弹性板的声辐射阻尼、不同板厚以及不同板边长尺寸下，弹性板声辐射阻尼随频率变化情况。

2 结构声系统的有限元/边界元分析

2.1 声振耦合的FEM/BEM方法

弹性结构在流体介质中受激振力作用引起的声辐射，为弹性体与流体耦合的问题。在结构振动方程中，除了结构所受的已知载荷外，还需要考虑声场对结构的作用力，从而形成一个耦合方程[12]。对于结构振动与声场耦合的数值求解方法，存在有限元法(FEM)[13]、边界元法(BEM)以及有限元与边界元结合的方法(FEM/BEM)[14，15]。本文结构采用有限元法近似，声场采用边界元法近似。

首先，利用有限元法建立结构的自由振动方程，同时利用边界元法得到流体对结构表面的作用力，将两者组合即建立了结构流体耦合方程。通过对耦合方程的求解，即可得到结构表面振速，进而根据Reyleigh积分关系利用边界元法得到声压以及其它声辐射特性。

考虑小振幅声波，进行线性化处理后，根据运动方程、连续性方程和物态方程，三维声场波动Helmholtz方程为：

2P+k2P=0

(1)

式中，P为介质中声压力；k为波数，k=ω/c；ω为声波频率；c为介质中声速。

流固交界面上边界条件满足：

(2)

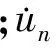
考虑理想流体介质，其Helmholtz波动方程可以转化为Rayleigh积分形式：

(3)

由式(3)可得流体动压力为：

(4)

对流固耦合交界面进行离散，将流体面力转换到节点上的节点力，有：

(5)

再将式(5)代入结构振动方程：

(6)

可以得到流体固体耦合运动方程[16]：

(7)

式中，[MA(ω)]为流体附加质量矩阵：

式中，[A]为流固交界面面积对角矩阵。

对耦合方程式(7)进行求解，得到结构表面振速，利用边界数值积分得到声压以及其他声辐射特性。

2.2 结构与流体数值模拟单元

在耦合系统数值模拟中，本文结构采用4节点四边形板壳单元，每个节点考虑5个自由度(u,v,w,θx,θy)，单元坐标和节点编号如图1所示。

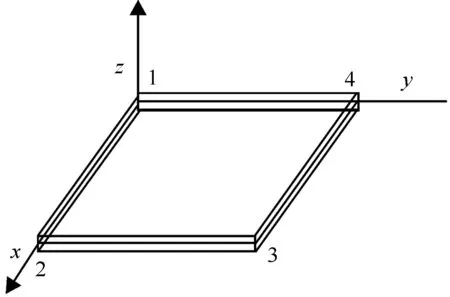
图1 单元坐标及节点编号图

根据Mindlin假设的板一阶剪切理论，采用双线性Lagrange插值。板内任意点的位移场和等参单元插值函数可分别表示为：

(8)

(9)

式中，u0、v0和w0分别表示所在板中面X、Y和Z轴方向位移；θx和θy分别表示所在板中面绕X和Y轴方向转角。

在利用式(3)计算流固耦合边界流体动压力时，需要对整个流场进行数值模拟，经过变换处理，使用边界元法可以使积分空间降低一维，由三维转换为二维。在进行流固耦合边界划分时，也采用4节点四边形单元。利用式(4)可以进行流固耦合交界面的数值模拟。

采用边界元方法,在利用式(4)计算结构表面声压时，式(4)中含有格林函数：

(10)

式中，r为场点S与源点Q之间的距离。

进行流体数值模拟时，为了和交界面上结构离散相一致，流体单元也是采用4节点二维线性单元。在单元循环计算的过程中，当场点S与源点Q重合时，即r=0处，积分存在奇异性，本文所采用的是蜕化单元法处理的奇异单元。近场和远场采用不同的积分阶数，保证计算精度的同时减少计算量。

3 声辐射阻尼

3.1 结构振动阻尼

结构振动特性受影响于结构的质量、刚度及阻尼。系统振动过程就是显现为系统动能与势能的连续不断转化，在转化过程中，部分能量以热能或其他形式耗散掉。动能含量与惯性有关，势能含量与刚度有关，而耗散能的大小取决于阻尼。所谓结构阻尼就是结构系统发生振动时，以热能方式耗散机械能的属性。阻尼描述方法常见的包括：

1) 阻尼的对数衰减率法，即自由振动系统中，采用对数衰减率，第n次波振幅Xn对第n+1次波振幅Xn+1比值的对数，作为结构阻尼值的一种度量；

2) 频响函数中阻尼描述方法也叫半功率法，适于描述受迫粘性阻尼系统或滞迟阻尼系统的阻尼；

3) 振动系统能量与耗散能量的阻尼表示方法，采用阻尼因子，即结构在振动一个周期中，能量的损耗与系统总能量之比，来衡量阻尼的大小与振动能损耗的多少[17]。

3.2 声辐射阻尼

当结构发生振动时，结构会对周围的流体介质进行压缩产生声波，声波通过流体介质向远场辐射，即形成了声辐射。与此同时，结构的一部分能量可以声能的形式传递到远场，这样结构的振动能量就发生了耗散现象，声辐射阻尼就产生了。声辐射阻尼往往大于结构振动阻尼。

结构的振动响应总是与它周围的流动介质有关。这些介质会改变结构的响应特性，在一定情况下，这个改变是值得考虑的，它能导致噪声向流体介质辐射，有时也会使结构的固有频率和振型产生明显的变化。

本文采用能量法，将声辐射阻尼定义为振动一周内系统以声波辐射的形式耗散的能量与结构振动能量的比值。

3.3 声辐射阻尼的数学描述

按照本文上节对声辐射阻尼的定义，声辐射阻尼可以写为：

(11)

式中，ER为周期内辐射能量；ES为周期内结构最大动能；W为辐射声功率；T为结构振动周期；ω为结构振动源频率。

将振动的弹性板表面分割成有限个振动面元，面元的最大几何尺寸应远小于声波波长，若每个振动面元可以看成独立声源的假设成立，根据线性叠加原理，设第i个面元上的复声压和复振速分别为pi和vi，则第i个面元的净辐射声功率为：

(12)

式中，ΔSi为第i个面元的面积。

将弹性板剖分成N个面元，如果每个面元是均匀的，且声压和法向振速组成的N阶列矢量分别为P和V，则板总的声功率为：

W=(ΔS/2)Re(VHP)

(13)

式(13)中上角标H表示对矢量实行共轭转置。声压和结构表面振速存在如下关系：

P=ZV

(14)

式中，Z为N×N阶传输阻抗矩阵。

对于无限大障板上的矩形平板，传输阻抗矩阵的第(i,j)元素为第j个面元上的声压比上第i个面元上的法向振速为：

zij=(jωρ0ΔS/2πrij)e-jkrij

(15)

整理之后有：

W=(ΔS/2)Re(VHZV)=VHRV

(16)

式中，R=(ΔS/2)Re(Z)。

这种计算声功率的方法表达式简洁，适合用于数值计算，而且便于求解不规则结构振动声辐射功率。本文的算例就是依据这种方法来计算结构的辐射声功率，结构振动最大动能可由下式计算得到：

(17)

式中，ρS为板结构密度；h为板厚；ui为i单元形心处振动速度。

将式(16)与式(17)代入式(11)，即可得到声辐射阻尼的计算表达式：

(18)

4 声辐射阻尼数值算例

根据上述结构和流体的物理模型，编制了相应的计算机程序，并且对典型算例进行了声辐射阻尼数值分析。

取一嵌于无限障板中的四边简支弹性板，分别考虑空气和水介质的影响。弹性板长度为0.8 m，板宽度为0.6 m，板厚度为4 mm，结构的材料密度为7 850 kg/m3，结构材料的弹性模量为210 GPa，泊松比0.3；水密度取1 000 kg/m3，水中声速为1 500 m/s；空气密度取1.29 kg/m3，空气中声速340 m/s。结构有限元单元和流体边界单元取同样的网格，如图2所示，分别对板处在半无限轻流体与重流体环境中的声辐射阻尼进行计算。

图2 弹性板有限元划分网格图

4.1 轻流体/重流体中板声辐射阻尼比较

弹性板分别处于轻流体与重流体中，选取激励大小为1 N，方向为垂直板面方向，作用位置为板的形心(0.4,0.3)处。通过对例板进行声辐射阻尼计算，得出重流体与轻流体中弹性板声辐射阻尼随频率变化,如图3所示。

图3 水中与空气中弹性板声辐射阻尼曲线

通过上图可以看出，随着激励频率的逐渐增大，板在水中与空气中振动的声辐射阻尼均为先增大然后趋于平稳。在外界激励相同的情况下，板在水中振动的声辐射阻尼远大于板在空气中振动的声辐射阻尼大小，这说明在相同激励作用下，弹性板在水中振动时的能量耗散能力远强于板在空气中时的能量耗散能力。

4.2 板厚对声辐射阻尼的影响

为了探讨弹性板板厚对声辐射阻尼的影响，本文选取与上节相同的激励，在板的其他参数不变的前提下，取板厚为3 mm、4 mm与5 mm，分别计算得出水中与空气中不同板厚下板的声辐射阻尼结果如图4与图5所示。

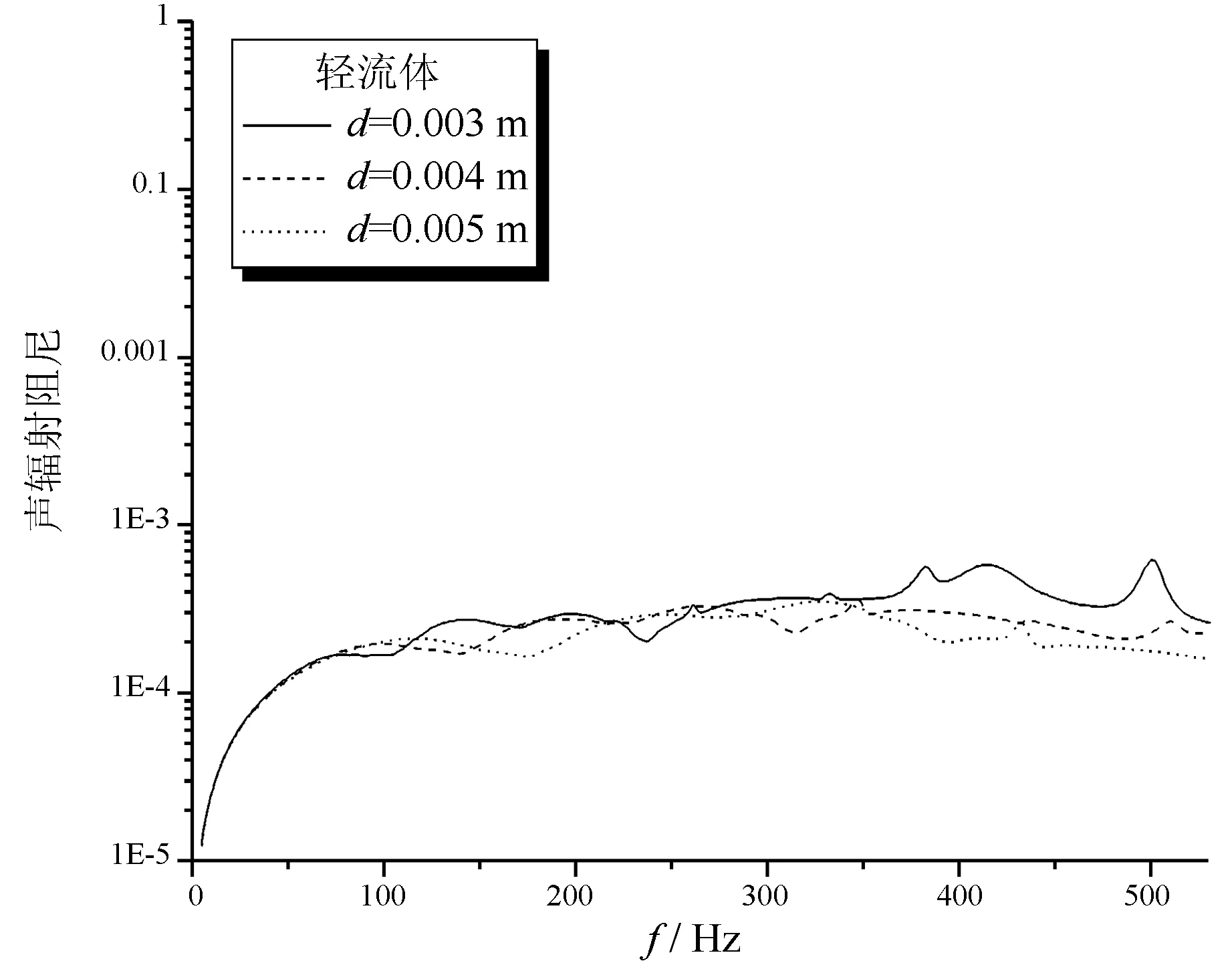
图4 空气中不同板厚下板的声辐射阻尼曲线

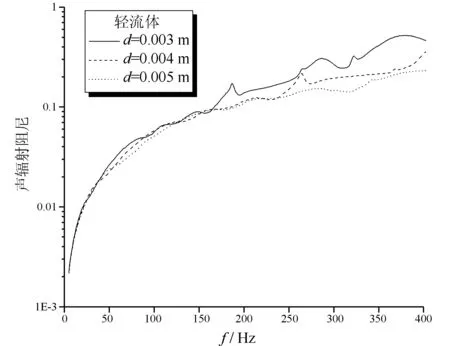
图5 水中不同板厚下板的声辐射阻尼曲线

通过图4与图5对空气中与水中弹性薄板在取不同厚度时的声辐射阻尼曲线的比较看出，在激励频率较小时，板厚对声辐射阻尼几乎没有影响；当激励频率较大时，板的声辐射阻尼随板厚的不同而稍有差异。总的来说，相同尺寸的弹性薄板的板厚对相应声辐射阻尼几乎没有影响。

4.3 板的尺寸对声辐射阻尼的影响

接下来探讨弹性板的尺寸对声辐射阻尼的影响，并选取与上节大小与方向相同的激励。在取板厚为4 mm，板的其他参数不变的前提下，取相同长宽比的3块弹性板，1号板长为0.8 m，宽为0.6 m；2号板长为1.2 m，宽为0.9 m；3号板长为1.6 m，宽为1.2 m。激励位置均为板的形心处，分别计算3块板在水中和空气中振动的声辐射阻尼，得出水中与空气中不同尺寸板的声辐射阻尼结果如图6与图7所示。

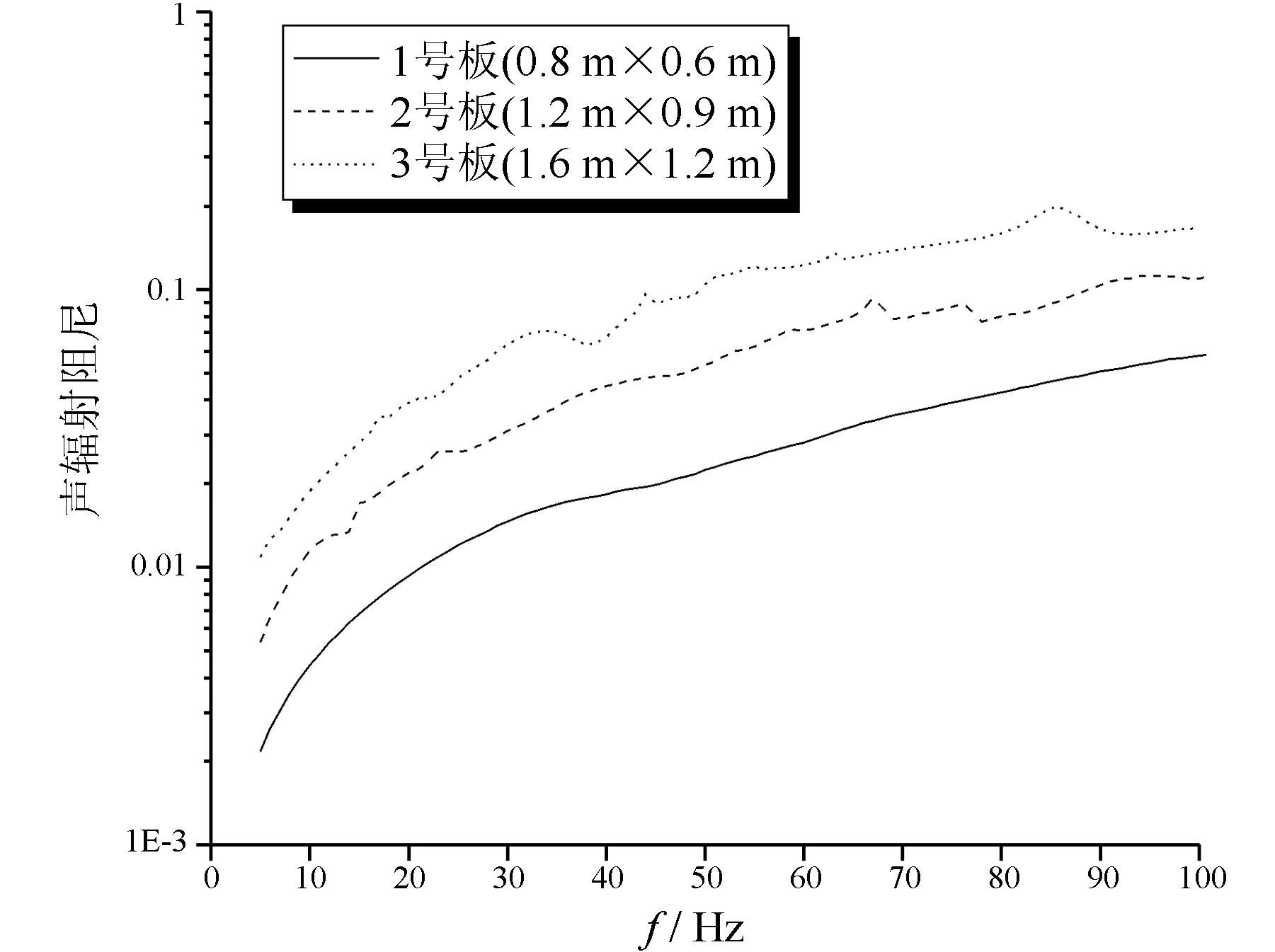
图7 水中不同尺寸板的声辐射阻尼曲线

通过图6与图7对空气中与水中弹性板在取不同尺寸时的声辐射阻尼曲线的比较看出，其他参数相同的弹性板取不同尺寸时，对相应声辐射阻尼是不同的。在相同激励频率下，弹性板的声辐射阻尼具有随板尺寸的增大而增大的变化趋势。

4.4 激励位置对声辐射阻尼的影响

上文讨论的均为激励位置一定时，弹性板不同厚度与不同尺寸时，声辐射阻尼随频率变化的情况。本节探讨声辐射阻尼因激励位置的变化而改变的规律。选取如图1所示的弹性板，激励大小为1 N，方向为垂直板面方向，位置分别选为点(0.1,0.1)、点(0.2,0.2)、点(0.3,0.2)与板的形心(0.4,0.3)处，对相应激励点下空气中与水中弹性板的声辐射阻尼进行计算，得出不同激励位置情况弹性板声辐射阻尼比较图，如图8与图9所示。

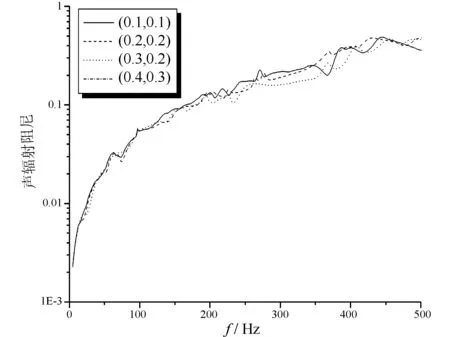
图9 水中不同激励位置时板声辐射阻尼比较图

相同的弹性板在激励位置不同时，其辐射能量不同，同时板结构所具有的最大动能也不同，然而，其两者相比得到的声辐射阻尼大小基本相同。通过图8与图9对空气中与水中弹性板在取不同激励位置时的声辐射阻尼曲线的比较看出，在激励频率较小时，激励的位置对弹性板的声辐射阻尼影响甚微；当激励频率较大时，不同激励位置弹性板相应的声辐射阻尼差异也是很小的。通过上述实践，说明激励的位置对弹性板声辐射阻尼几乎没有影响。

5 结 论

本文通过相应算例的计算分析，得出了弹性板声辐射阻尼随板的不同厚度、板的不同尺寸以及不同激励位置的变化规律：

1) 弹性板在水中的声辐射阻尼远大于在空气中的声辐射阻尼；

2) 相同尺寸的弹性薄板的板厚对相应声辐射阻尼几乎没有影响；

3) 在相同激励频率下，弹性板的声辐射阻尼具有随板尺寸的增大而增大的变化趋势；

4) 弹性板的声辐射阻尼不随激励的位置变化而变化。

[1] 孙庆鸿,等.振动与噪声的阻尼控制[M].北京:机械工业出版社,1993.

[2] 许士桐.船舶结构阻尼处理技术[J].造船技术. 1990 (1):21-25.

[3] 伏同先．阻尼技术及其在舰船减振降噪中的应用[J]．噪声与振动控制,1985(9):97-104.

[4] 徐雪英.振动阻尼技术[J].国外导弹技术,1991(1):62-93.

[5] MUHLSTEIN L,Jr. Experimental evaluations of the aerodynamics damping of skin panels at low supersonic Mach numbers,in proceedings of the 13thstructures[C]. Structural dynamics and materials conference.AIAA.，1972: 72-402.

[6] LYLE K H,DOWELL E H.Acoustic radiation damping of flat rectangular plates subjected to subsonic flows. PartⅠ: Isotropic[J].Journal of fluids and structures, 1994(8):711-735.

[7] LYLE K H,DOWELL E H.Acoustic radiation damping of flat rectangular plates subjected to subsonic flows.PartⅡ: Composite[J].Journal of fluids and structures. 1994(8): 737-746.

[8] WALLACE C E.The acoustic radiation damping of the modes of a rectangular panel[J]. Acoust. Soc. Am，1987，81(6):1787-1794.

[9] KRIEGSMANN G A,SCANDRETT M A.Assessment of a new radiation damping model for structural acoustic interactions[J]. Journal of the Acoustical Society of America.1989.86:788-794.

[10] 郭新毅.含损伤加筋板结构振动与声特性变异研究[D].大连:大连理工大学,2004.

[11] 郭新毅,洪明.含损伤加筋板结构声辐射阻尼变异研究[J].船舶力学.2007,11(4):628-636.

[12] 柯兵.基于ANSYS二次开发实现结构体声辐射数值计算及其主动控制[D].武汉:华中科技大学,2002.

[13] 詹伟东.加筋板流固耦合振动分析及几何非线性研究[D].武汉:武汉交通科技大学,1999.

[14] 周健.板结构的声辐射与隔声性能研究[D].武汉:华中科技大学,2002.

[15] 童宗鹏.船舶结构的流固耦合振动与声辐射研究[D]. 华东船舶工业学院,2004.

[16] 付喜华,洪明,等.舰船加筋结构声辐射数值模拟方法研究[C].第十一届船舶水下噪声学术讨论会,2007.

[17] 周端国.阻尼技术及其应用[J].电讯技术,1985(1):47-51.