内部含基座的加筋双层壳振动与声辐射计算

1 引 言

有限长加筋双层圆柱壳是潜艇舱段结构的主要形式，研究其在流场中受激振动后的声辐射对潜艇隐身技术有着重要意义。Evseev[1]研究了流场中无限长纵向加筋圆柱壳的声辐射问题，纵骨沿周向等间距分布，把纵骨处理为反力和反力矩作用，在与壳体连接处，反力和扭矩的表达式用纵骨的机械阻抗乘以连接处的纵骨的振速，声压也用辐射阻抗表达，用Fourier变换展开壳体的位移函数。Yoshikawa[2，3]研究了无限长不加筋双层壳在流场中的声辐射性能，通过傅氏变换在K空间中求解内外壳体的径向位移。文献[4]提出共振声辐射理论，并分别以球壳和有限长圆柱壳体的水下耦合振动问题为例验证了该理论，并分析和阐述了壳体结构的声振特性及声辐射产生机理。目前,大多数的研究均忽略了壳体内部结构的存在，直接将激励力施加在壳体内壁。在实际工程问题中，壳体内部总是存在某种结构，如基座，而产生激励的机械安装在基座上，激励力通过基座再作用到壳体上。壳体内部基座相当于一个机械滤波器，它对振动和声辐射有着重要影响。

Achenbach[5]曾研究了具有内部简单子结构(弹簧振子系统)的柱壳的声辐射特性。由于所考虑的结构十分简单，仍可能用解析方法处理。在一般情况下，只要结构稍微复杂一些解析方法就无能为力。数值方法(有限元+边界元方法)原则上能够处理任意复杂的结构，但计算工作量大、速度慢，且难以直接进行机理分析。本文结合数值、解析方法[6]，利用两种方法各自的优点，采用有限元数值方法计算基座对壳体的激励力，而壳体的振动及声辐射由解析解给出，从而能对具有复杂内部结构的双层加筋壳体声辐射特性进行研究。本文基于数值/解析的方法，讨论了内部含有基座的复杂加肋双层圆柱壳的振动及声辐射问题，这对于水下壳体结构的减振降噪设计具有重要实际意义。

2 基本理论

2.1 计算模型及坐标系

本文的计算模型简化为浸没在无限流场中的有限长加筋双层圆柱壳，坐标系和壳体的几何参数如图1所示。

图1(b)为坐标系，径向坐标向外为正。假设流场是均匀无粘无旋的无限流场，满足线性声学条件，并认为结构变形在线弹性范围内。

图1 双层壳几何模型及坐标系

2.2 运动方程

双层圆柱壳运动采用Flügge壳体理论描述，把托板视为动反力作用在壳体上，其振动方程[7]为：

{-{F}T-{fr}T-{ft}T-{qi}T}

(1)

式中[Lijk] (i=1,2分别代表内、外层壳体，j,k=1,2,3)为采用Flügge理论的壳体微分算子，惯性项和静水压力项均包含在内，壳体、环肋、纵骨、托板和实肋板采用相同的材料；E为壳体杨氏模量；v为泊松比；Ri为内、外壳体的半径；hi为壳板的厚度；{ui}T={uiviwi}T表示壳体轴向、周向和径向位移；{F}T为作用在壳体上的激励力；{fr}T为环肋的反力；{ft}T为托板的反力；{qi}T={0 0qir}T为辐射声压。两层壳间充满流体，双层圆柱壳位于无限外流场中，各反力具体的求解过程可参考文献[7]。

方程(1)的形式解如下(略去时间因子e-jωt)：

(2)

式中，α=0,1分别对应壳体周向对称及非对称振动;m,n分别为轴向半波数和周向波数。

声压满足Helmholtz波动方程

(3)

式中，x为声场中任意一点;ω为激励力频率;C为流体中的声速。

2.3 边界条件

为了便于分析，在研究其振动声辐射问题时，假设双层圆柱壳两端连接着无限长刚性障板，满足简支边界。

1) 位移边界条件

v=w=Nx=Mx=0 (x=0,L)

2) 流固交界面条件

式中，ω为激励力频率；ρw为流体介质密度。

2.4 激励力

假定激励力作用在内壳上，壳体受到的激励力分解为:

(4)

(5)

将上式代入式(4)中并对所有节点叠加，可得到

(6)

式中,εn是Neumann因子，当n=0时，εn= 1；n≠0时，εn= 2。将上述各式代入Flügge壳体运动方程，即可进行水中双层圆柱壳耦合振动方程的求解。

2.5 方程的求解

令

(7)

式中

用[A]乘以方程(1)的两边，并沿壳体表面积分，利用壳体固有模态的正交性和δ函数的性质，壳体的运动方程即可化为：

(8)

具体求解过程可参考文献[7]。

2.6 壳体声辐射性能的表示

辐射声功率是声源机械功率中的有功部分，壳体表面的辐射声功率大小反映了壳体表面辐射声波本领的高低，壳体表面的径向均方速度表示壳体在流场中的结构响应，同时也表示声源振动的平均速度。

(9)

(10)

式中，Znmm是双层壳n,m阶振动的自辐射阻抗；S是壳体外表面；*表示共轭复数。

声功率级、径向均方速度级分别定义为：

(11)

上式中，声功率级和速度级的基准为：

W0=10-12(W)；V0=5×10-8(m/s)。

3 壳体激励力的计算

本文采用有限元数值解法求解基座对激励力的传递。在计算基座对力的传递作用时，为了节省计算时间，可忽略壳体向流体中的声辐射的影响，而只考虑结构的振动问题，这是因为壳体因振动产生的声辐射能量与振动自身的能量相比是很小的，下文将对此进行数值验证。本文对外壳体外的水介质进行简化，在双层壳模型外添加少量流体声单元，同时内外壳间充满流体，以此来进行结构中基座传递力的计算。

双层壳尺寸为：R1/h1=125，R1/l1=5.83，R1/L=0.583，R2/h2=466.7，R3/l2=3.267，R2/L=0.653，其中L为双层圆柱壳的长度，R1,h1,l1分别为内壳体的半径、厚度和内壳环肋间距；R2,h2,l2分别为外壳体的半径、厚度和外壳环肋间距;托板沿轴向等间距分布，间距为l3=l2，厚度为h3=2.67h2，基座面板厚度为t，基座轴向长度为lF，且lF/L=0.164。使用ANSYS软件对整个壳体模型建模并划分网格。双层壳采用壳单元建模，材料为钢，且E=2.1e11 N/m2，ρ=7 850 kg/m3，v=0.3。结构阻尼取为0.02，集中激励力为100 N。壳体有限元网格模型见图2。

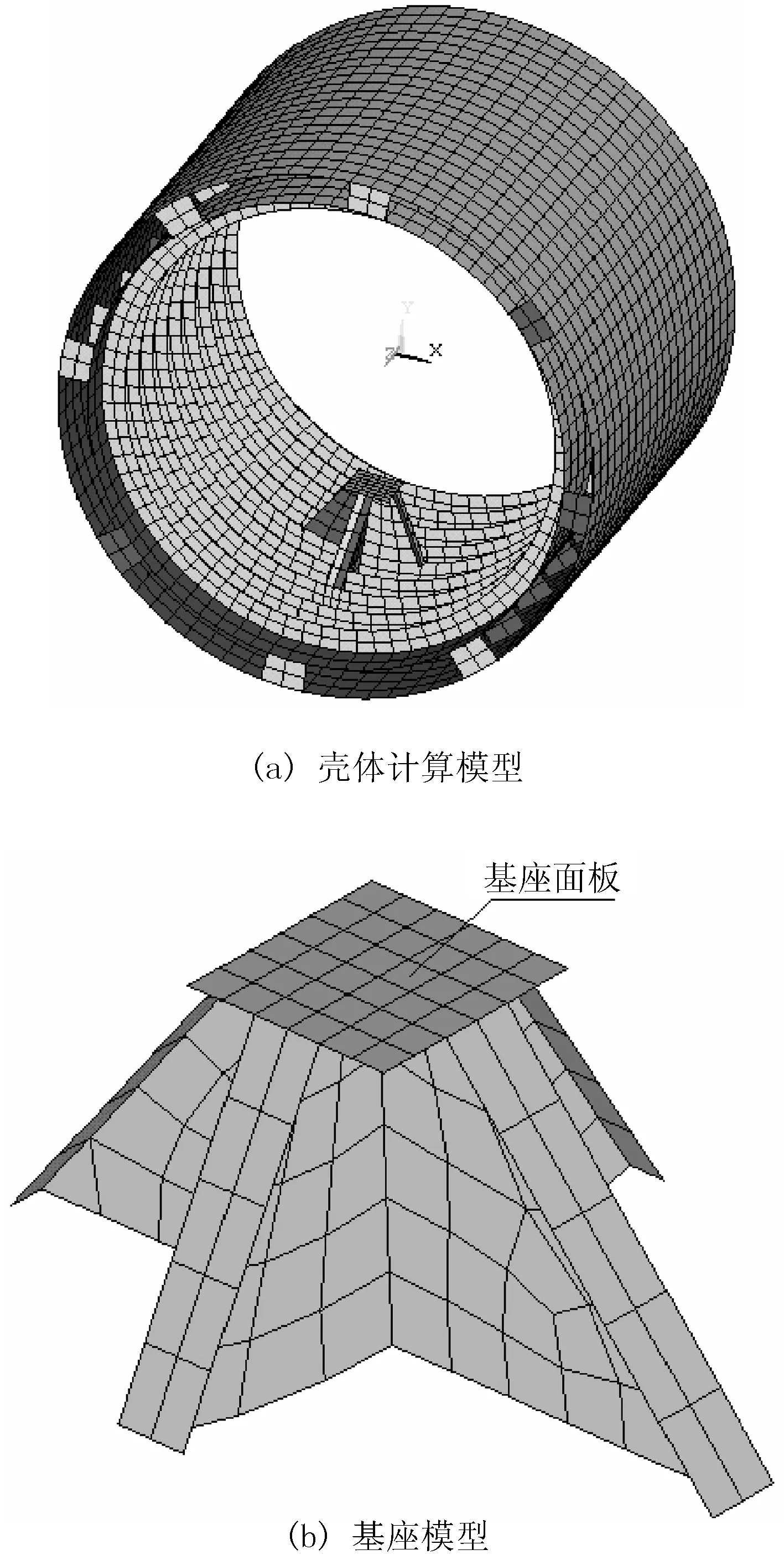
图2 壳体有限元网格模型

通过数值计算可得到基座对壳体作用力的频谱图，计算频率范围为0～500 Hz。图3给出了节点力随z轴位置变化曲线；图4给出了节点力随频率的变化曲线。可以看出，各节点轴向力相对其它方向激励力较小，由于壳体的对称性，径向力沿z轴方向呈现对称性，而切向力沿z轴方向呈现反对称性。将计算得到的壳体节点作用力代入式(6)中，即可进行壳体在水介质中声辐射计算。

图3 节点力随z轴位置变化曲线

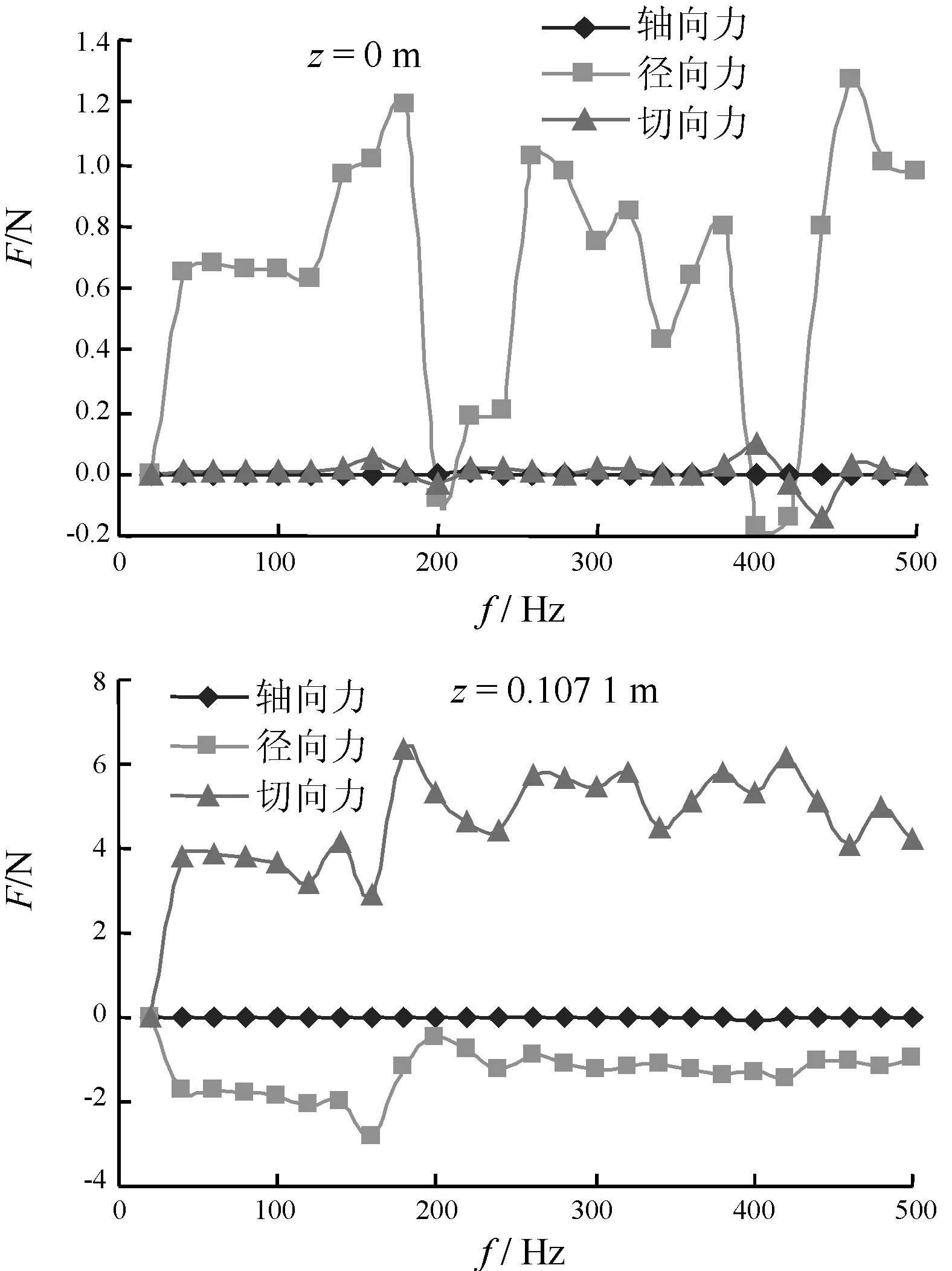
图4 节点力随频率的变化曲线

4 壳体振动声辐射计算

4.1 基座对壳体声辐射的影响

本文中采用有限元法计算基座对壳体振动传递力时，对壳体外部水介质进行了简化，为了验证此方法的合理性，图5给出了是否考虑壳体外部水层对基座传递力影响时，计算所得到的壳体辐射声功率对比曲线。图中“壳体外无水层”即进行基座对壳体的作用力有限元计算时忽略了外部水介质对激励力的影响。从图5中可以看出两种方法计算得到的双层壳辐射声功率几乎是相同的，这说明当基座的尺寸相对壳体较小时，用解析的方法估算壳体振动声辐射可以忽略外部水介质对壳体激励力数值计算的影响。

图5 激励力数值计算中水层对壳体辐射声功率的影响

图6 均方速度级对比曲线

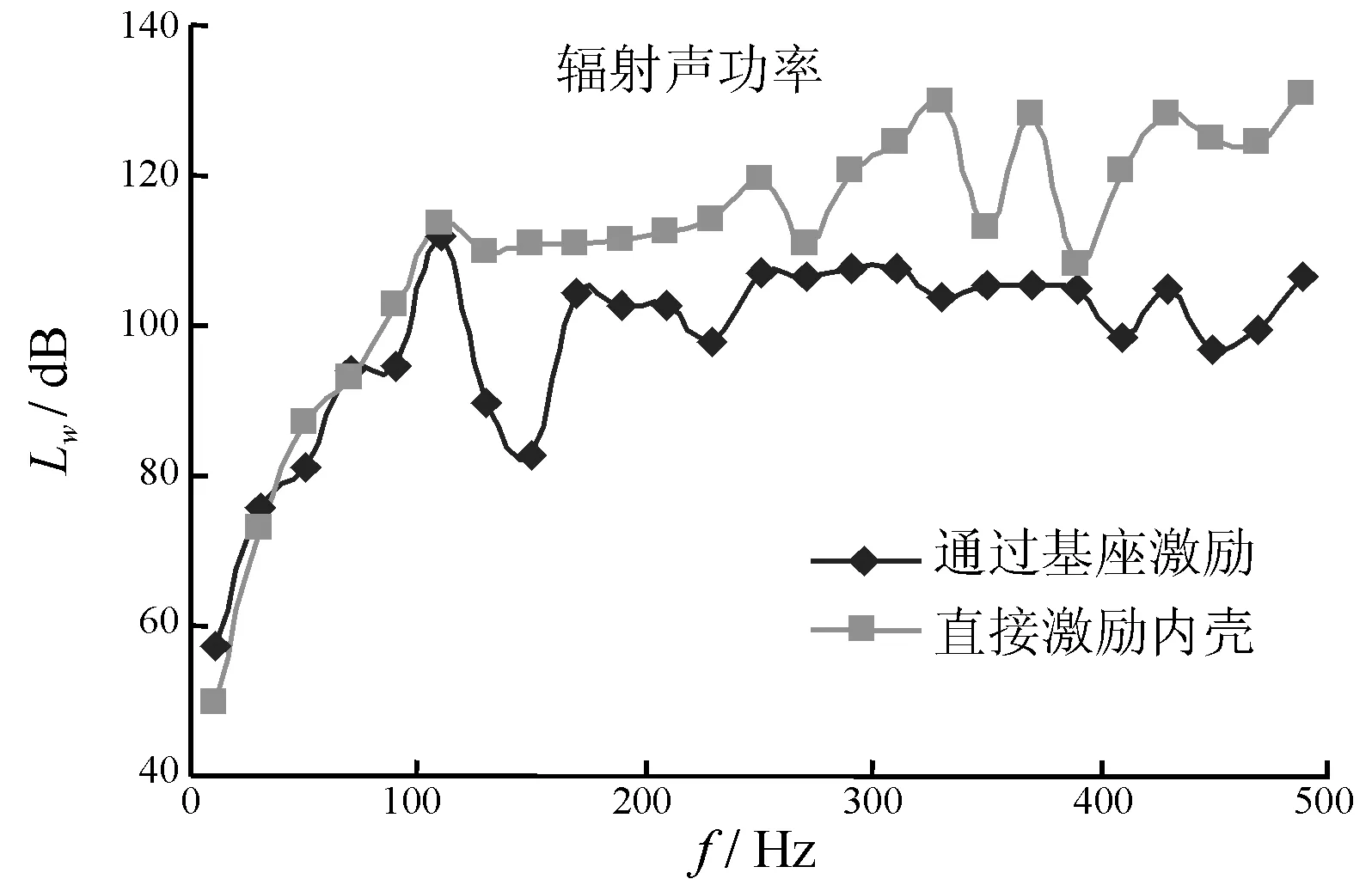
图7 辐射声功率对比曲线

图6、图7给出了集中力直接径向激励内壳、内壁与基座时，外壳均方速度级对比曲线以及结构辐射声功率对比曲线。从图6可以看出，当激励力通过基座作用到壳体时，外壳振动均方速度级在0～500 Hz范围内均有明显的降低，即基座的存在有效降低了壳体的振动。这是因为增加基座后，圆柱壳系统的总质量增加，导致壳体的振动强度减弱。从图7可以看出，100 Hz以下两条曲线几乎重合；100 Hz以上，基座的存在有效降低了双层壳的辐射声功率。由此可以得出，壳体内部基座的存在，相当于壳体内增加了一个机械滤波器，其有效降低了壳体振动声辐射，在进行水下航行体声辐射特性研究时，必须将壳体内部结构考虑在内。

4.2 基座尺寸对壳体声辐射的影响

接下来讨论基座尺寸变化对双层壳声辐射性能的影响。图8、图9给出了基座面板加厚为2t时(t为原基座面板厚度)，外壳振动均方速度级及结构辐射声功率曲线。可以看出，基座面板厚度加厚后，外壳振动均方速度级以及结构辐射声功率均有所降低。这是由于面板加厚后，增大了板的抗弯刚度，使得结构的机械阻力增加，基座振动激励度降低，导致双层壳结构振动声辐射下降。另外还可以看出，曲线中共振峰的位置没有改变，因为它们是由壳体的固有频率特性决定的。

图8 均方速度级对比曲线

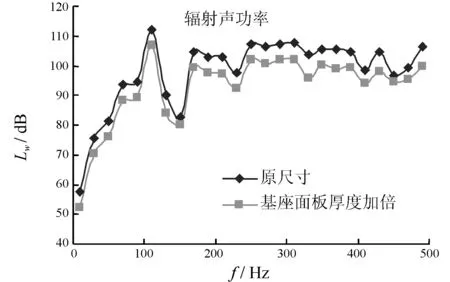
图9 辐射声功率对比曲线

图10、图11给出了基座轴向长度变为原长度1.5倍时，外壳振动均方速度级及结构辐射声功率曲线。可以看出，当基座尺寸增大，即其质量增大，壳体总体振动声辐射水平有所降低。

图10 均方速度级对比曲线

图11 辐射声功率对比曲线

4.3 激励力作用位置对壳体声辐射的影响

在实际水下航行体建造过程中，由于各种各样的原因，动力设备的安装难免会有所偏离基座中心位置，因此，研究激励力作用位置对壳体振动声辐射的影响具有重要的意义。图12、图13给出了激励力位置沿纵轴水平偏离基座中心1/4a时(a为基座面板长度)，外壳振动均方速度以及圆柱壳辐射声功率曲线。从图12可见，当激励力偏离基座面板中心时，外壳振动均方速度曲线共振峰位置发生变化，这是由于激励力偏离壳体中心位置后，激起了壳体的非对称模态，引起共振峰位置发生变化。总之，除部分峰值增大外，均方速度变化不是很大。从图13同样可见，除部分共振峰值发生变化外，结构辐射声功率总体变化不大。

图12 均方速度对比曲线

图13 辐射声功率对比曲线

5 结 论

本文基于数值/解析的方法，讨论了内部含有基座的复杂加筋双层圆柱壳的振动及声辐射问题，主要得出以下结论：

1) 采用本文计算方法分析内部含基座结构的壳体振动声辐射问题是完全可行的。并且,当基座尺寸相对壳体较小时，采用有限元法对基座传递力进行计算时，可以忽略外壳外部的水介质所产生的影响；

2) 壳体内部增加基座降低了壳体的振动及声辐射，并且增加基座面板厚度或者基座长度均能有效降低壳体的振动声辐射，这对水下航行结构减振降噪设计具有重要的指导意义；

相同结构尺寸下，当激励力偏离基座面板中心位置后，除共振频率及部分共振峰值发生变化外，结构的振动均方速度及辐射声功率总体变化不大。

[1] EVSEEV V N. Sound radiation from a shell reinforced with longitudinal stiffeners [J]. Sov. Phys. Acoust, 1989, 35(6):624-627．

[2] YOSHIKAWA S, WILLAMS E G, WASHBURN K B．Vibration of two concentric submerged cylindrical shells coupled by the contained fluid[J]．J Acoust. Soc. Am.，1994，95 (6): 3273-3286．

[3] YOSHIKAWA S. Fluid-structure coupling by the entrained fluid in submerged concentric double-shell vibration [J]. J Acoust. Soc. Jp.(E), 1993, 14(2): 99-111．

[4] 汤渭霖,范军.水中球壳的共振辐射理论[J]．声学学报, 2000, 25(4)：308-312．

[5] ACHENBACH J D, BJAMASON J, IGUSA T. Effect of a vibrating substructure on acoustic radiation from a cylindrical shell[J]. Transactions of ASME, 1992, 114: 312-318.

[6] 刘涛,汤渭霖,何世平.数值/解析混合方法计算含复杂结构的有限长圆柱壳体声辐射[J].船舶力学, 2003, 7(4)： 99-104.

[7] 陈美霞．有限长加筋双层圆柱壳声辐射性能分析[D]．武汉：华中科技大学博士学位论文，2003.