不对称型双体船初稳性研究
2008-04-24贾敬蓓,宗智,师华强等
1 引 言
近年来,多体船型一直广受人们的关注,有关多体船方面的研究也成为人们研究的热点。然而不管是以前的单体船还是目前人们广泛关注的多体船,它们都是属于对称型的船体。对于不对称船型,公开报道的也只有2003年由中国烟台莱佛士船厂制造完成的一艘名为Asean Lady的大型游艇[1],如图1所示。虽然人们已经开始注意到不对称船型,甚至已经制造出不对称型的游艇,但是对于不对称船型的理论研究,目前,还鲜见公开发表的研究结果或论文。

图1 Asean Lady 游艇
所谓不对称船型概念是相对于传统的对称船型而言的,是指船体水线下横剖面形成不对称形状的船型。单体船和双体船甚至多体船都可能出现不对称船型。为了研究方便,我们选择不对称双体船型进行研究,如图2所示。
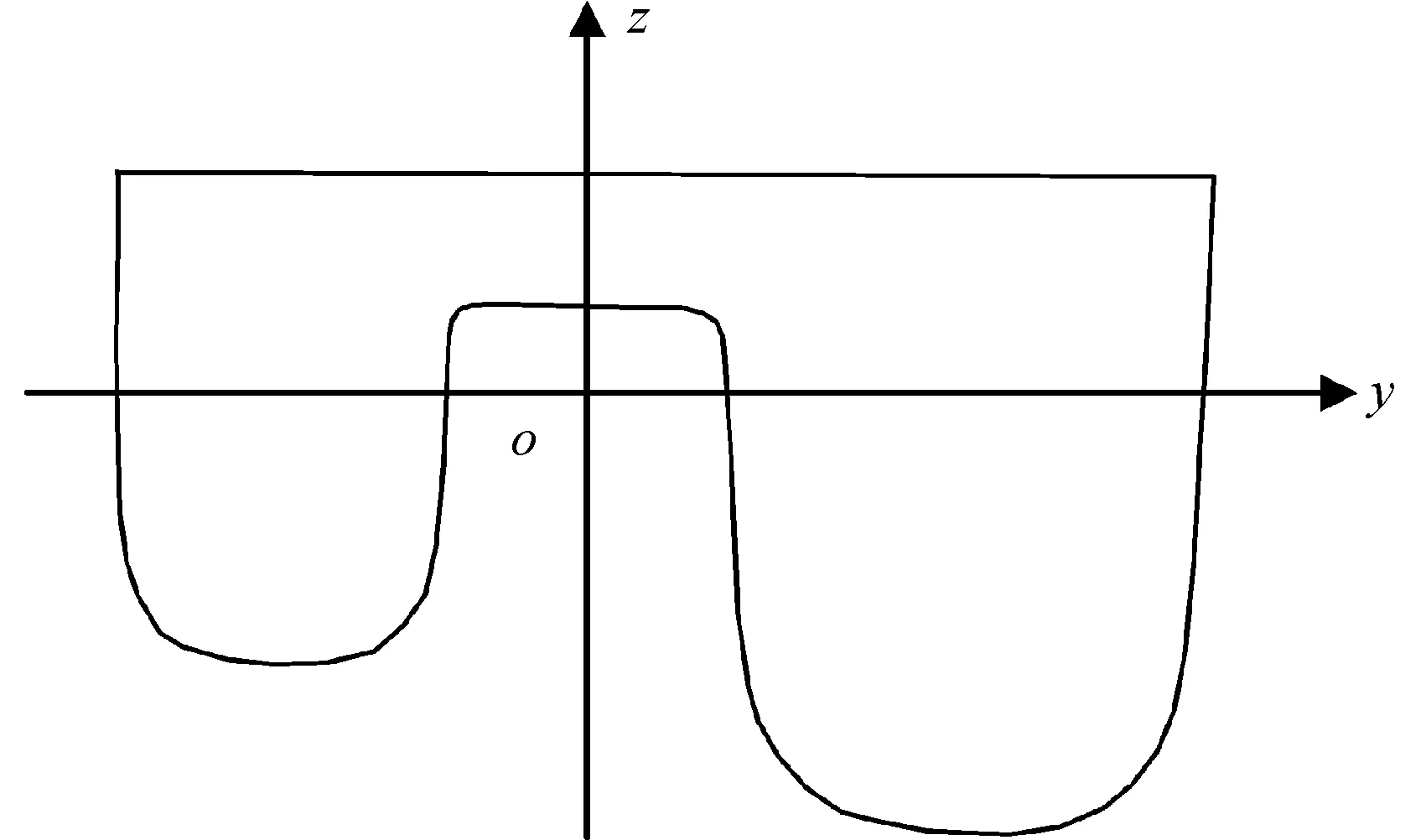
图2 不对称双体船横剖面示意图
船舶稳性是评价船舶性能好坏最基本的指标之一,因此有必要对这种新船型进行这方面的研究。本文仅仅讨论了不对称船舶的初稳性,亦称小倾角稳性。由于水线下船体横剖面的不对称性,传统中计算船舶初稳性的公式将不再完全适用于不对称船体,所以应该重新推导适用于不对称船体的初稳性计算公式[2,3]。
2 理论模型及公式推导
2.1 理论模型的建立
根据船舶静力学知识可知,船舶的初稳性可以由初稳性高GM的值来衡量。初稳性高GM可以由公式:GM=BM+ZB-ZG求得,其中的B,G,M各点如图3所示,它们分别表示船舶水下体积的形心、船舶重量重心和船舶稳心;公式中的BM是船舶的稳性半径,ZB是船舶水下体积形心的垂向坐标;ZG是船舶重量重心的垂向坐标;这一公式同样适用于不对称船舶。

图3 船体小倾角时各参数示意图
由于ZB可以通过数值计算很简便地计算得到,ZG一般可以通过经验公式估算或根据装载状态计算得到。因此,求初稳性高的关键就是要求出稳性半径BM的值。由船舶静力学可知BM=BB1/φ。对于传统对称船型,因为有BB1=(IT/)·φ,即可得BM=IT/,再通过水线面半宽做简单的积分数值运算就可以算出IT和,从而得到稳性半径BM的值。但是对于不对称船舶,由于水线面左右是不对称的,不能直接利用水线面各半宽值直接积分得到IT和,所以就必须重新推导用于不对称船体的BM计算公式。
初稳性高是一个物理量,它的数值结果和所选取的坐标系位置无关。为了研究方便,选取如图2所示的坐标系,即坐标系原点O取为船舯横剖面上的设计水线处主侧体间隔的中点;z轴沿竖直方向,向上为正;y轴沿船宽方向,指向右舷为正;x轴沿船长方向,指向船首为正。
不对称型船的左倾和右倾初看起来不同,但是,我们的研究表明左倾和右倾的初稳性公式却是一样的。其原因是在小倾角情况下,左右是等体积倾斜的,所以,初稳性对于左倾和右倾是一样的。下面我们只针对右倾进行研究。
2.2 初稳性高公式推导
2.2.1不对称船体的等体积倾斜
设船体平浮时水线为WL,在外力作用下的横倾小角度φ后的水线为W1L1,在此种情况下,船舶仅仅受到倾斜力矩的作用,排水体积保持不变。因此,倾斜后的水线W1L1是等体积水线,此时的倾斜为等体积倾斜,即出水体积=入水体积。由此可确定出倾斜水线W1L1的位置。
但是,对于不对称船型来说,等体积倾斜水线并不是将原平浮水线绕着坐标系的原心偏斜小角度φ后的水线W′L′,在左右船体不对称的条件下,为保证出水和入水体积相等,就必须要求等体积水线应该在水线W′L′的基础上平移一段距离,以满足等体积倾斜的条件。如图4中的水线W1L1。
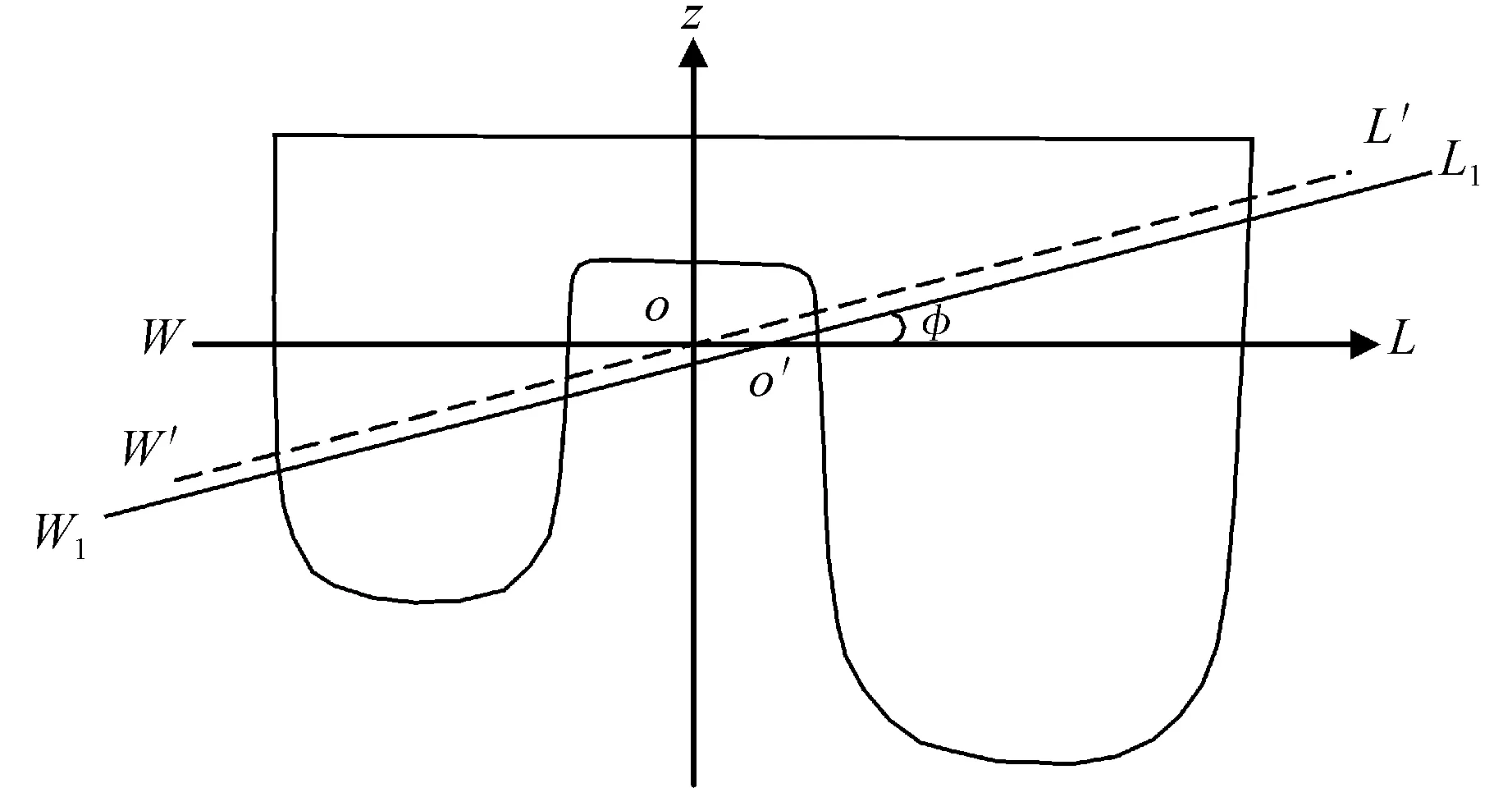
图4 等体积倾斜示意图
设两侧船体间距的最大值为b,左侧船长设为l,右侧船长设为L。图5中,ym表示右侧船体的船宽,yw表示左侧船体的船宽,yL表示以z轴为基准左侧的船体宽,yR是以z轴为基准右侧的船体宽。h是等体积倾斜水线在水平方向偏移的距离。v1,g1,v2,g2分别表示出水体积、入水体积及其重心位置。
从图5可以看出,等体积水线偏移的距离在小于b/2和大于b/2两种情况下,船体出水体积和入水体积的表达式是不一样的。因此,等体积水线的偏移距离应该分成这两种情况分别计算。

图5 偏移距离h≤b/2
2.2.2等体积水线偏移距离的计算
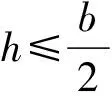
(1)
经推导可得:
(2)
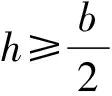
(3)

图6 偏移距离h≥b/2
此时,式中参数S1,S2的表达式为:
经推导可得:
(4)
由最终推导出的h的公式可以看出,在h≤b/2和h≥b/2这两种情况下,h的表达式是一致的,只是出水体积及入水体积的表达式在这两种情况下是不同的,所以只需要计算出h的值,然后将其与b/2比较,在h≤b/2和h≥b/2时,分别使用对应的出水体积、入水体积和重心公式进行计算即可。
2.2.3初稳性高公式
假设已经求出h的值,现在分情况讨论:
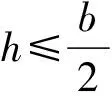
yL-yw+h
(5)
yR-ym-h
(6)
由于g1g2=g1o′+g2o′,v1=v2=v,φ在微小角度时tanφ≈φ,所以有:
g1g2·v=(g1o′+g2o′)·v=g1o′·v1+g2o′·v2
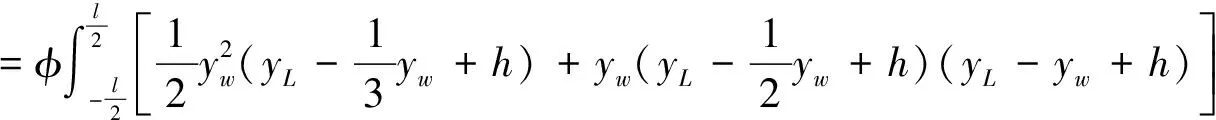

(7)
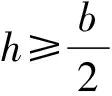
(8)
(9)
同理可得:
dx+
(10)
至此,g1g2·v的表达式也已经推导完毕。
由重心移动原理可知:
(11)
则由关系式:
(12)
即可导出BM的表达式:
(13)
(14)
dw,dm分别为左右侧船体吃水。
3 不对称双体船分析讨论
依据上述推导得出的公式,作者编制了一个计算不对称双体船初稳性高的FORTRAN程序。只需要输入相应的船体参数,即可以运行计算出船体的初稳性高。
下面首先以两艘单体船为例来验证此程序的可行性和精确性。一艘单体货船的主尺度是:L=74.0 m,B=13.0 m,T=4.5 m,根据船体具体型值按照静力学公式BM=IT/可以计算得到BM=3.15 m;通过运行编制的程序得到结果BM=3.12 m。同理,对一艘主尺度为L=31.0 m,B=6.6 m,T=2.5 m的单体渔船进行计算,由公式BM=IT/计算的结果为BM=1.75 m,运行程序所得结果为BM=1.74 m。通过上面两个算例可以看出,此程序具有可行性和足够的精确性。
下面本文将就不对称双体船的初稳性进行某些分析讨论,不妨将两个船体中较大的一个称作主体,另一个较小的称作侧体。所选用的不对称双体船主尺度如表1所示,剖面示意图及各种参数表示如图7所示。
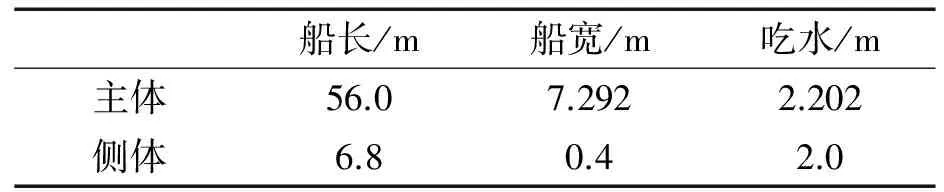
表1 不对称双体船主尺度
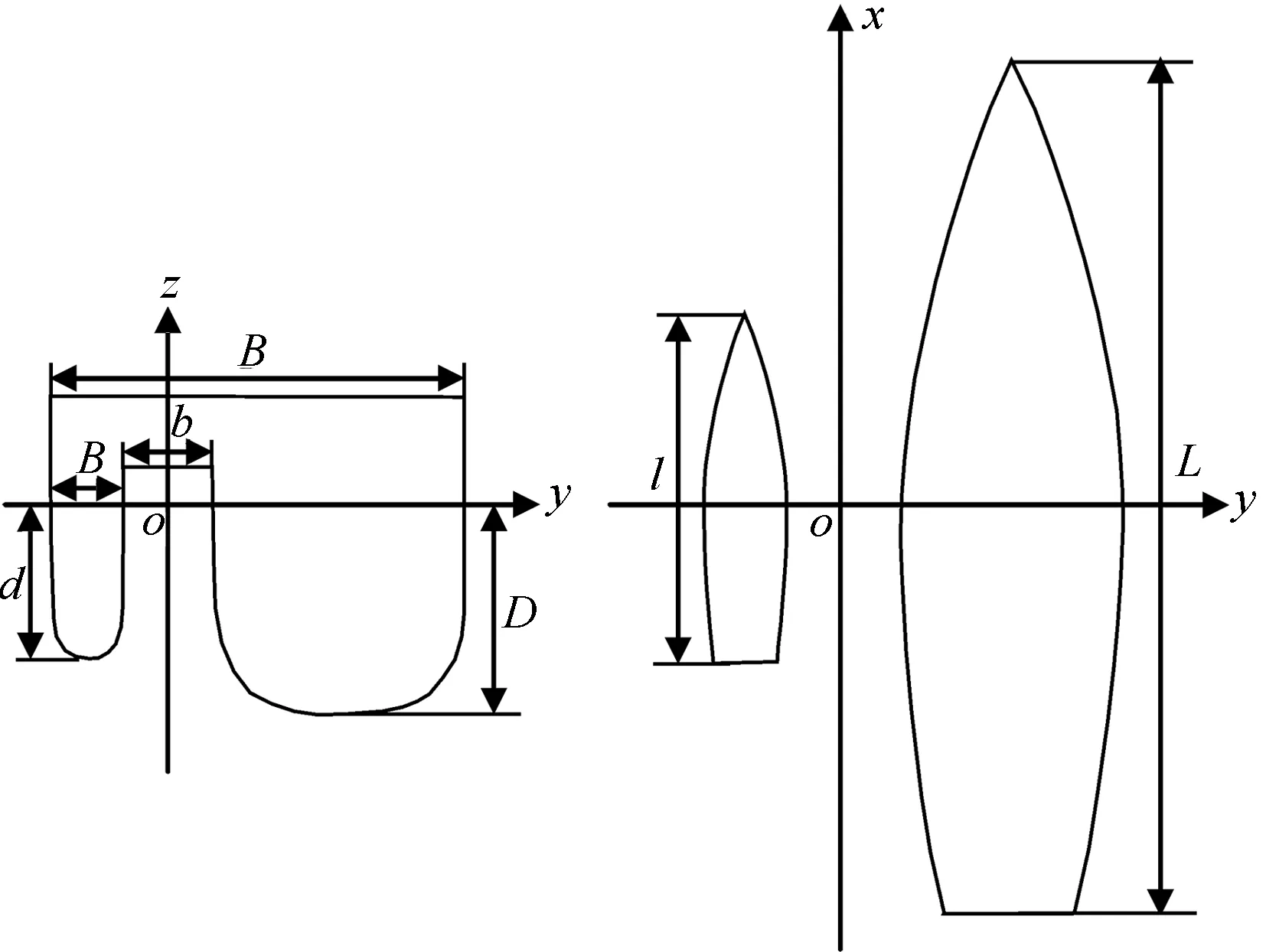
图7 不对称双体船剖面示意图
本文在假定不对称船主体固定不变的前提下,详细讨论了侧体的几个主要参数对初稳性高的影响。这些参数分别是:侧体与主体之间的跨距b,侧体船长l,侧体船宽B1,侧体吃水d。为了更直观地表示上述参数的变化情况,不妨将这几个参数分别转换成以下变量:间距b与总船宽B的比值b/B,侧体船长l与主体船长L的比值l/L,侧体船宽B与总船宽B的比值B1/B,侧体吃水d与船体总吃水D的比值d/D。下面将分别讨论这4个变量对初稳性高GM的影响,并假定一个变量变化时,其余变量都是固定不变的。具体结果如图8~图11所示。
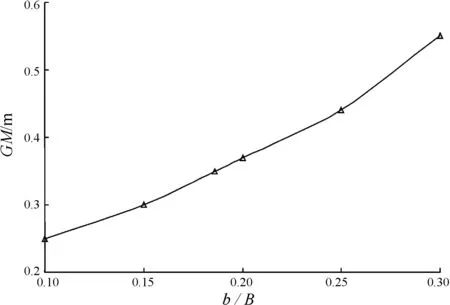
图8 初稳性高GM随b/B变化曲线

图9 初稳性高GM随l/L变化曲线
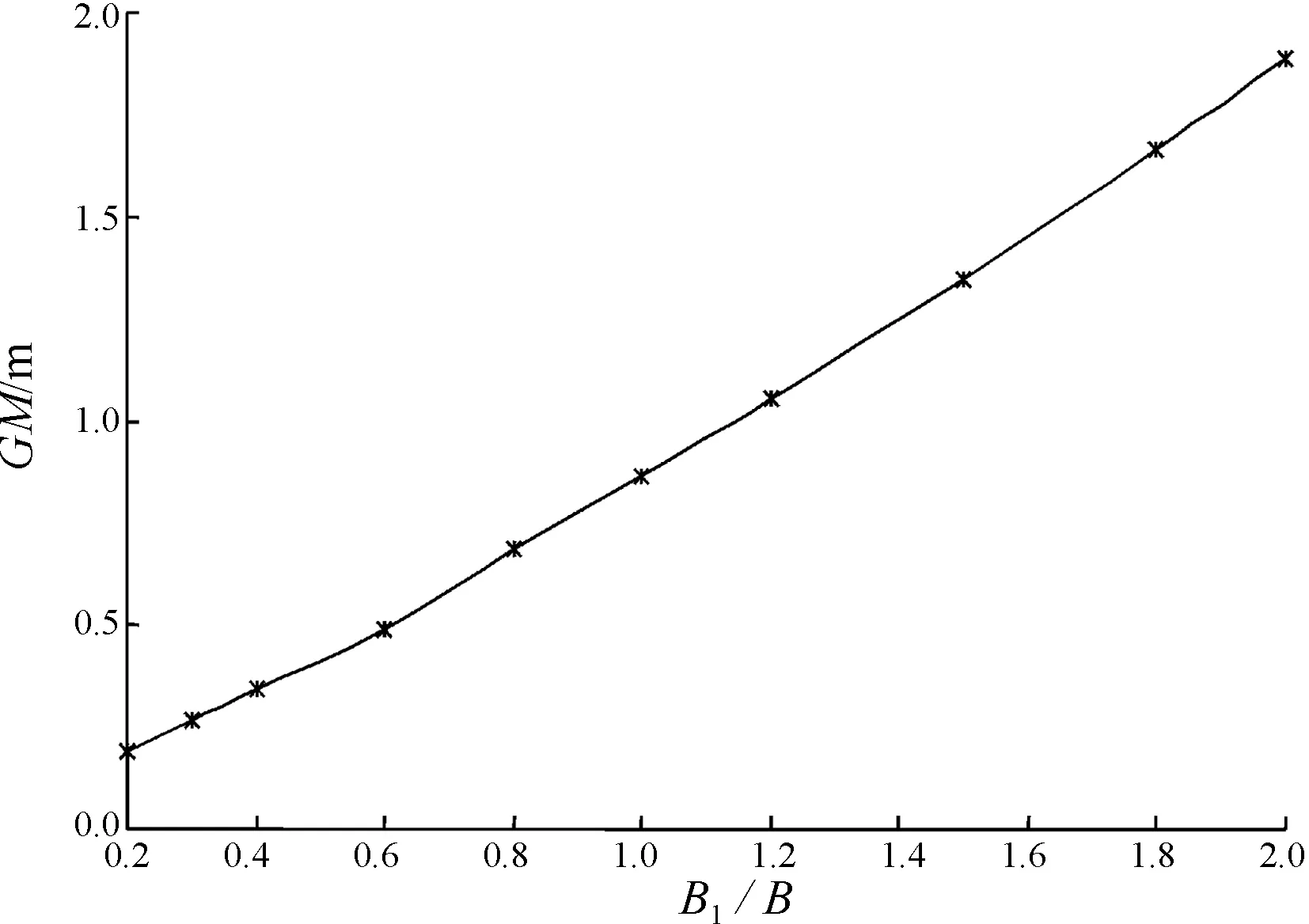
图10 初稳性高GM随B1/B变化曲线
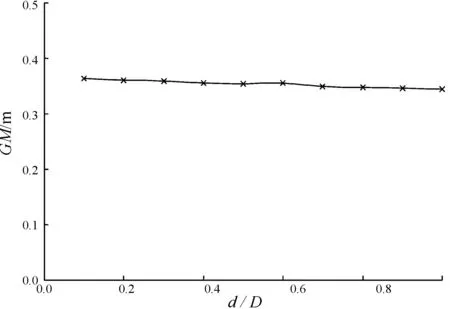
图11 初稳性高GM随d/D变化曲线
4 结 论
1) 本文对不对称船舶初稳性进行了初步研究,所编写的FORTRAN程序可以计算出不对称船的初稳性高,为不对称船初稳性的判断提供依据。同时,本程序还适用于计算对称船型的初稳性高。
2) 由本文的分析可以看出,对不对称双体船初稳性影响较大的参数是:主侧体之间的距离、侧体船宽和侧体船长,而且,随着这些参数值的增大不对称船体初稳性高也在增大。而侧体吃水对初稳性高的影响不大。
[1] News Singapore. Asean lady sea trials in September. http://www.rafflesyacht.com/images/news-update/Yachts%20Asia-Pacific.pdf.
[2] 盛振邦,杨尚荣,陈雪深.船舶静力学[M].上海:上海交通大学出版社, 1992.
[3] 李培勇,裘泳铭,顾敏童,许统铨.多体船型完整稳性计算[J].上海交通大学学报, 2002, 36(11): 1560-1563.
