基于模糊神经网络和D-S证据理论的故障诊断方法研究

1 引 言

20多年来，基于解析模型的故障诊断方法在理论研究及应用领域引起广泛重视[1]。但随着科学技术的发展，设备结构日趋复杂，故障的非线性更强，很难获得精确完善的系统模型。无模型的故障诊断方法回避了抽取对象的数学模型，日益受到国内外学者的关注。目前，基于无模型的故障诊断技术主要有Kullback信息准则故障诊断[2]、故障树分析诊断[3]、专家系统[4]、基于神经网络的故障诊断[5]等。由于神经网络具有处理非线性和自学习以及并行计算等方面能力，在非线性系统的故障诊断方面具有较大的优势，但它对系统具有“黑箱”特性，没有明确的物理意义。同时，这种方法只能利用原始数据，无法吸收人类的宝贵经验。而模糊逻辑的结构参数具有明确的物理意义，系统可以充分利用前人的经验知识，不过针对复杂系统，许多可调参数的确定是一项非常复杂的过程。

文中将模糊逻辑与神经网络融合起来构造的模糊神经网络，具有模糊逻辑和神经网络各自的优点[6]，再用D-S证据理论进行全局融合，使融合结构从信号的有效组合出发，充分利用各种信息，提高了诊断的精度[7-8]，并通过算例验证了方法的有效性。

2 基于模糊神经网络和D-S证据理论故障诊断方法的实现

从故障征兆空间提取信号，然后将信息向子模糊神经网络分配；诊断模块中的子模糊神经网络为并联结构，分别从故障发生的不同侧面进行故障诊断；输出结果经过归一化处理，满足基本可信度分配函数的条件，进行信息融合，即可得到最终故障诊断结果。

故障诊断的具体流程见图1。

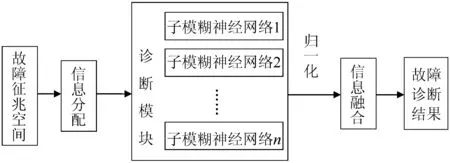
图1 故障诊断流程

2.1 模糊神经网络的结构

文中构造如图2所示的网络结构。整个网络由4层组成，分别是输入层、模糊化层、模糊推理层和输出层。

1) 输入层。将故障征兆参数作为模糊神经网络的输入。

2) 模糊化层。其作用是对输入量进行模糊化处理，即根据隶属函数求出每一输入的模糊变量值。

3) 模糊推理层。该层实现输入量模糊变量值到输出量模糊变量值的映射。

4) 输出层。输出量为故障发生的置信度。

图2 模糊神经网络的结构

网络训练采用改进的反向传播算法：

设有学习样本(x1p,x2p,…，xmp;tp)(p=1，2，…，p；p为样本数)，在随机给出网络连接权向量W后，按反向传播法得出网络的输出值为yp，对于样本p，网络的输出误差为：

dp=tp-yp

(1)

误差函数为：

(2)

其学习过程就是不断地调整向量W的值，逐步降低误差dp，提高网络计算精度。学习过程采用的是优化计算中的梯度下降法，即沿着误差函数ep随W变化的负梯度方向对W进行修正。设ΔW为W的修正值，则：

(3)

式中,η为学习效率，取0∶1间的数。

当能量函数对应的误差曲面为窄长型时，这种算法在谷的两壁跳来跳去，需要对其增加附加动量项，则修正值ΔW得迭代公式为：

(4)

式中,α为动量因子，一般取接近1的数。

根据公式(4)不断进行迭代，当输出误差达到要求时，结束网络训练。

2.2 D-S证据理论全局融合

D-S证据理论[9-10]有以下基本定义：

定义1 在证据理论中，一个样本空间称为一个辨识框架，用θ表示，它是对某些问题的可能答案的一个集合，但其中只有一个是正确的。若辨识框架θ中的元素满足互不相容的条件，命题A对基本概率赋值函数m赋值，m(A)是集合2θ到[0,1]的映射，m(A)称为事件A的基本可信度分配函数。

满足条件：

(5)

定义2 如果辨识框架的一个子集为A，且m(A)>0，则称θ的子集A为信任函数Bel的焦元。信任函数Bel定义为：

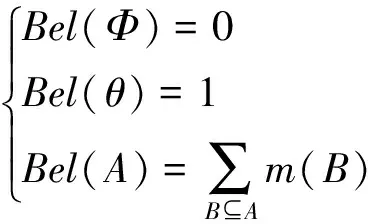
(6)

合成法则 假设m1和m2是两个相同辨识框架θ上的基本可信度分配函数，如果Bel1的焦元是A1,……，Ak，Bel2的焦元是B1，……，Bn。对于各种证据，来源不同具有不同的基本可信度分配函数，Dempeter提出利用正交和合并数据组合输出：

(7)

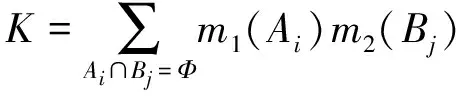
(8)

K反映出对于同一假设每个证据相互之间的矛盾程度。

3 算 例

设某艇导航设备有4种典型故障类型F1～F4， 通过传感器1能够获得征兆1、2的参数X1、X2， 且对故障F1、F2、F3的诊断有效；通过传感器2能够获得征兆3、 4的参数X3、X4， 且对故障F2、F3、F4的诊断有效。采用两个子模糊神经网络，网络1以X1、X2为输入，网络2以X3、X4为输入，F1、F2、F3、F4的置信度作为子网络的输出。训练样本如表1所示。

表1 训练样本

用表1的数据对网络进行训练，训练好后，就可以利用实际采样数据对故障诊断系统进行仿真。由一次采样得到的故障征兆参数(x1,x2,x3,x4)=(0.281，1.235，1.367，0.589)，进行仿真得到诊断模块的两组输出是(0.133，0.768，0.253，0.031)和(0.054，0.815，0.139，0.128)，归一化后得到表2。利用公式(7)进行信息融合。

表2 归一化后故障置信度

m(F1)=0.011m(F2)=0.931
m(F3)=0.052m(F4)=0.006

比较看出：最可能发生的故障为F2,置信度为0.931。融合后得到的诊断结果比任一子模糊神经网络的结果都可信。

4 结束语

由于模糊逻辑与神经网络两种系统的优势互补，使得模糊神经网络方法具有较强的自适应性、容错性、鲁棒性。文中提出的故障诊断方法既利用了模糊神经网络的优势，又利用了信息融合技术有效组合信号，从而提高了故障诊断的准确率。经算例验证了该方法的可靠性、有效性，对于复杂装备的故障诊断有一定意义。但由于反向网络结构的本质特性，使模糊神经网络的应用范围限制在只能处理静态问题。需应用于动态映射时，可考虑选择模糊递归神经网络。

[1] GARCIA F J，IZQUIERDO V，LUIS M J.de，et al.Faultdiagnostic system using analytical fuzzy redundancy[J].Engineering Application of Artificial Inteligence，2000，13(2)：441-450.

[2] KUMAMARU K.Robust fault detection using index of Kullback discrimination information[J].Proc.of IFAC World Congress，1996(14)：205-210.

[3] ANTIONIOC F G，NELSON E F.Fuzzy FTA：a fuzzy fault tree system for uncertainty analysis[J].Annals of Nuclear Energy，1999(26)：523-532.

[4] QIAN Yu，LI Xiuxi，WEN Yanrong，et al.An expert system for real-time fault diagnosis of complex chemical processes[J].Expert Systems with Applications，2003，24(4)：425-432.

[5] VEMURI A T，MARIOS M P.Neural network-based robust fault diagnosis in robotic systems[J].IEEE Trans.on Neural Netwoks，1997，8(6)：1410-1419.

[6] 丛爽.几种模糊神经网络系统关系的对比研究[J].信息与控制，2001，30(6)：486-492.

[7] 何友，王国宏.多传感器信息融合及应用[M].北京：电子工业出版社，2000.

[8] 李自荣，郭磊.基于信息融合的多层次故障诊断研究[J].航空兵器，2006，3，49-52.

[9] 魏雪云，廖惜春.一种基于证据理论的数据融合新算法研究[J].传感技术学报，2006，19(6)，2702-2706.

[10] 张淑清，邓红，王艳玲.D-S证据理论在数据融合中的应用及改进[J].传感技术学报，2003(1)78-81.