二维周期性结构的声波带隙研究
2008-04-24陈源,周明刚,周敬东
1 引 言
近年来,具有一定周期结构的复合材料的能带特性的研究越来越受到人们的关注,这是由于这种复合材料对经典波(光波、电磁波、超声波和声波等)具有良好的带通和带阻特性,在声学领域,能带之间出现的带隙称为声子带隙(phononic band gap),相应的这种复合材料称为声子晶体( phononic crystal)。最近10年,通过对大量复合材料的理论和实验研究,声子晶体已经取得很大的发展,根据声子晶体的带隙特性,可以看出该材料在工程中有着很好的应用前景。声子晶体的声子禁带,即处于声波带隙频率范围内的振动或声波被禁止在声子晶体中传播。晶体的拓扑结构是影响声子禁带的产生和大小的因素之一[1-5]。
2 二维二元无限周期结构的弹性波带隙
假设二维二元无限周期结构是由圆柱体A以正方点阵形式排列于基体B中组成的二维双组分复合材料体系,如图1所示。图中圆形黑点是圆柱体A,其原子质量为M,其它部分是基体材料B,其原子质量为m。周期长度矢的方向为X轴和Y轴方向。a为相邻A原子间距离;b为相邻B原子与A原子间的距离;c为相邻B原子间的距离。
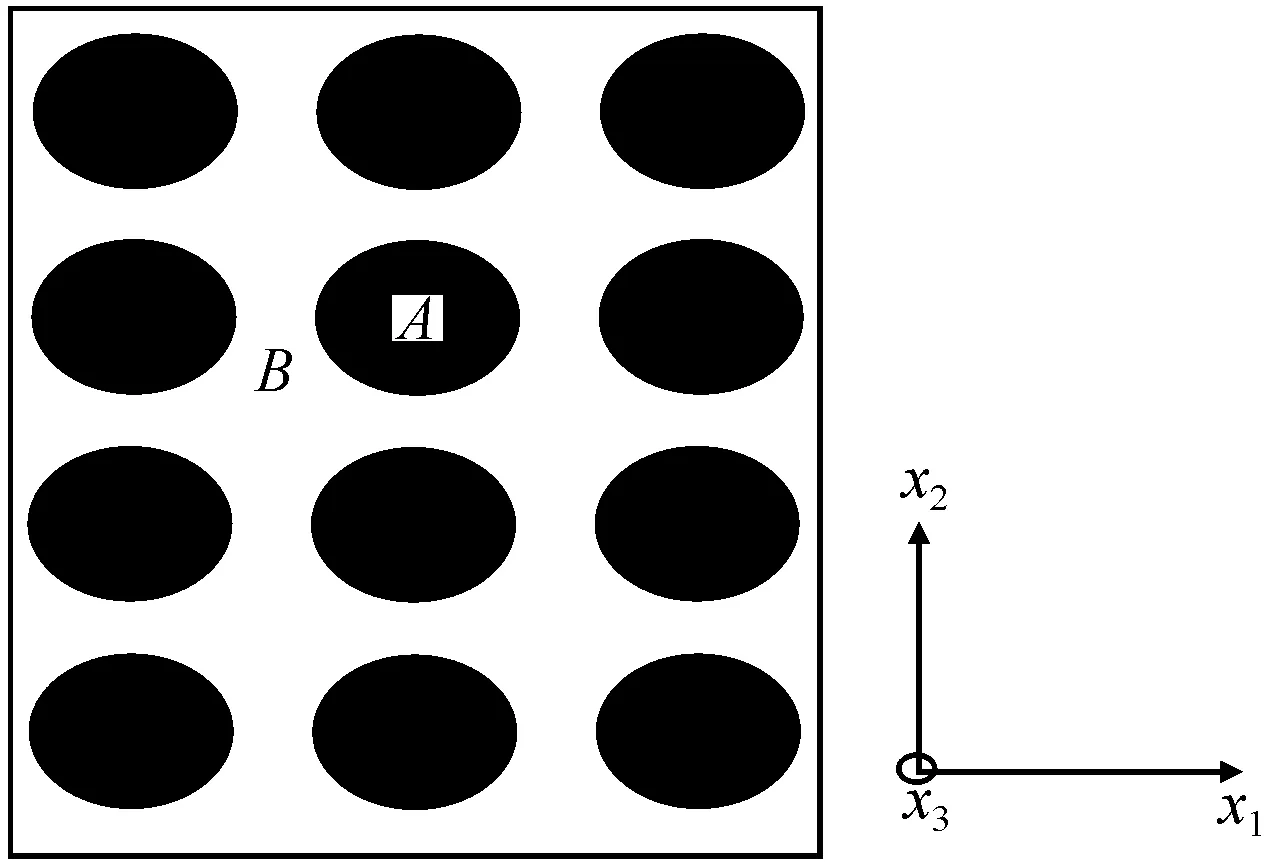
图1 二维二元无限周期结构的排列图
由于该结构原子的振动是极其复杂的,当波同时沿X任一方向传播时,相邻X轴和Y轴方向的原子的振动会受到干涉,也即X轴方向的原子偏离平衡位移时会受到Y轴方向相邻原子的作用,同时Y轴方向的原子偏离平衡位移时也会受到X轴方向相邻原子的作用。在X轴方向上同种M原子的力常数为β1,同种m间的力常数为β2,而相邻的M和m间的力常数为β3;在Y轴方向上同种M原子的力常数为k1,同种m间的力常数为k2,而相邻的M和m间的力常数为k3。为了便于建立二维二元无限周期结构模型的振动方程,可以把图1简化,二维二元无限周期质点加弹簧的结构如图2所示。图中棱形黑点为基体材料B的原子,圆形黑点为材料A的原子。

图2 二维二元无限周期质点加弹簧的结构示意图
由于该结构是周期性的结构,所以在X轴方向可以理解成图3(a)所示结构。我们来分析质量为M的第n0号和第n0+1号及质量为m的第1号原子和第n1号原子的振动模型。由图3(a)我们不难得出周期性结构在X轴方向的任意原子的运动图,见图3(b)。

图3(a) X轴方向结构示意
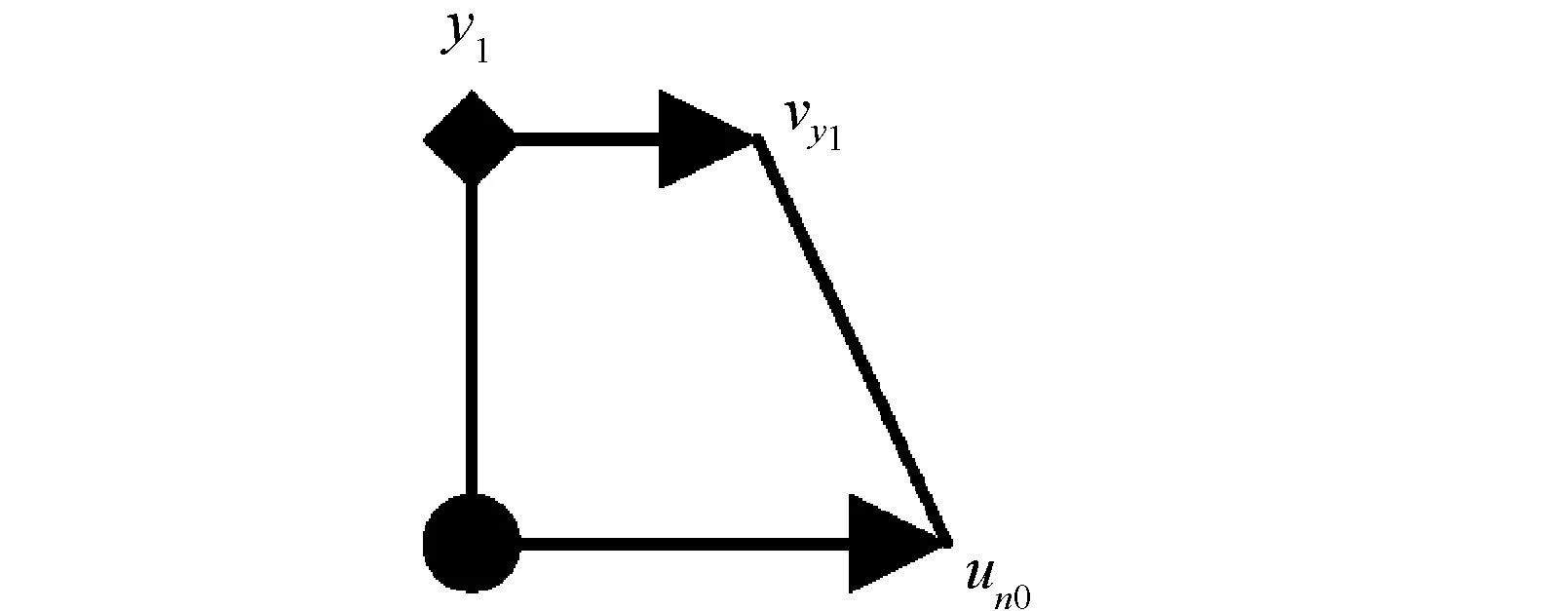
图3(b) 任意原子的运动
所以,可以得出第n0个材料A原子运动方程:
(1)
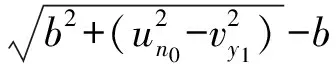
(2)
同理,可得出X轴方向其它原子运动方程为:
(3)
(4)
(5)
上述式中,vj表示X轴方向序号为j的基质材料B原子在t时刻偏离平衡位置的位移;ui表示X轴方向序号为i的材料A原子在t时刻偏离平衡位置的位移。
同理,在Y轴方向我们可以理解成图4(a)所示结构,主要分析为M的第n0号和第ny0+1号及质量为m的第1号原子和第n1号原子的振动模型。由图4(a)我们不难得出周期性结构在Y轴方向任意填充原子的运动图,见图4(b)。

图4(a) Y轴方向结构示意
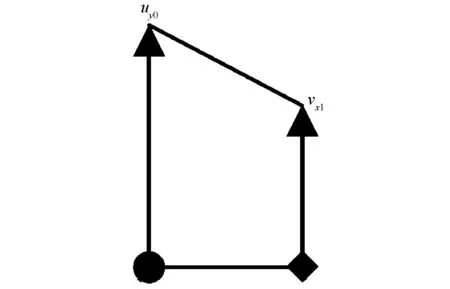
图4(b) 任意填充B原子的运动
所以,我们容易得出第ny0个填充B原子的运动方程:
(6)
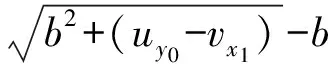
(7)
同理,可以得出Y轴方向其它原子的运动方程为:
(8)
(9)
(10)
上述式中,vyj表示Y轴方向序号为j的基质材料B原子在t时刻偏离平衡位置的位移;uyi为表示Y轴方向序号为i的材料A原子在t时刻偏离平衡位置的位移。
根据一维无限周期性结构声子晶体的带隙不难得出,在二维结构的两个周期矢方向上的弹性波带隙为:
ωx1max≤ωXD≤ωx4min
ωy1max≤ωYD≤ωy4min
式中
3 二维二元有限周期结构的振动传输特性
3.1 理论方法
根据无限周期结构,不妨假设有限周期二元二维结构的质点加弹簧的结构示意图为图5。由无限周期二维二元结构的分析可知:在微幅振动的前提下,二维周期结构可以近似看成独立的两条一维链结构,所以,也把有限周期结构看成X轴方向和Y轴方向上的两条独立的一维有限链结构。设X轴方向上的周期数为2N1,Y轴方向上的周期数为2N2。每个周期内有n1个材料A原子和n2个材料B原子。图6是第j周期的原子结构图。
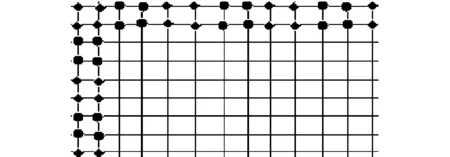
图5 有限周期二元二维结构的质点加弹簧结构示意图

图6 第j周期的原子结构
X轴方向第j周期时域离散的差分方程为:
(11)
(12)
式中,i=2,3,…,(n1-1)
(13)
(14)
(15)
式中,i=2,3,…,(n2-1)
(16)
同理,Y轴方向的差分方程可以写成:
(17)
(18)
式中,i=2,3,…,(n1-1)
(19)
(20)
(21)
式中i=2,3,…,(n2-1)
(22)
利用上述的式(11)~式(22)递推差分方程,当在已知u1(ux,uy)信号的激励下,可以求出任意时刻的输出信号v(v2N1n2,v2N2n2) 。把u1(ux,uy)和v(v2N1n2,v2N2n2)进行Fourier变化,两者频域的比即为频响曲线。
3.2 实例计算
下面以弹簧加非常薄质量块组成的二维二元结构为例。设X轴方向上的周期数为2,Y轴方向上的周期数为4。每个周期内有1个材料薄质量块A和1个材料薄质量块B,如图7所示的结构图。
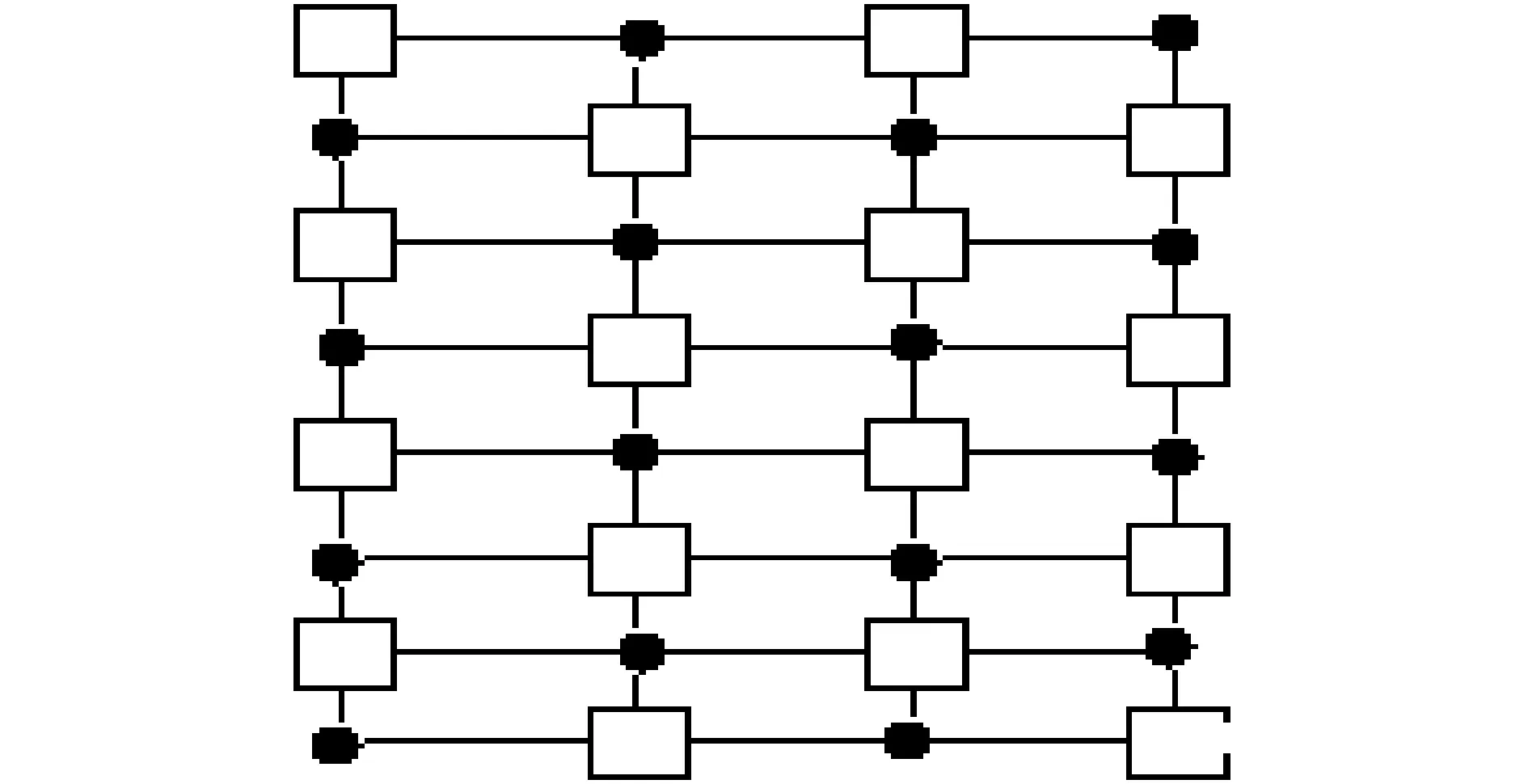
图7 非常薄质量块组成的二维二元结构示意图
图中方块为材料薄质量块A,其质量为M=2 kg;图中圆黑点为材料薄质量块B,其质量为m=1 kg;假设X轴方向的弹簧弹性系数为β=2 000 N/m,而Y轴方向的弹簧弹性系数为k=3 000 N/m;利用上述有限周期的二元二维周期结构的差分方程,我们可以得出图7结构的频响曲线为图8。
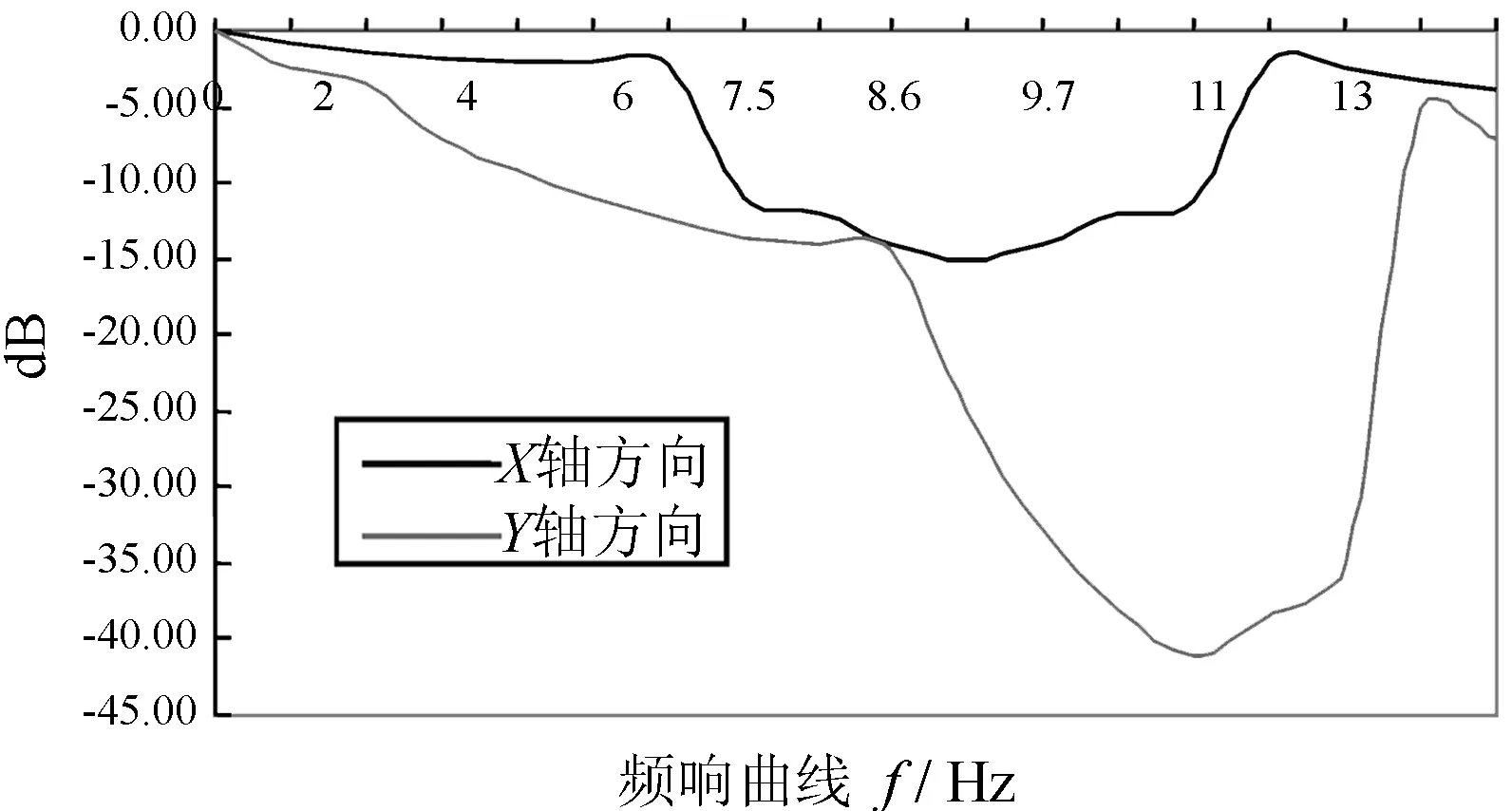
图8 X、Y轴方向的频响曲线
无限周期的二维二元周期结构的理论带隙X轴方向为7.1~10.1 Hz;Y轴方向的带隙为8.7~12.3 Hz;而对于图7的有限周期结构,其传输特性曲线由图8知,在X轴方向为6.9~10.2 Hz;而Y轴方向为8.5~12.1 Hz上有较大的衰减。所以不难得出:有限周期结构有较大衰减的频率范围与无限周期结构的弹性波带隙相一致,也就是说有限周期结构在弹性波带隙上,弹性波受到了明显衰减作用。
4 小 结
本文在一维声子晶体的基础上,着重研究了无限周期二维二元结构的弹性波带隙计算,并从实际需要出发,利用时域差分法计算了有限周期二维二元周期结构的振动传输特性曲线即频响曲线。通过实例计算本文得出如下成果:
1) 在满足微幅振动的条件下,无限周期二维二元周期结构可以简化成独立的两条无限周期结构的一维链来计算;
2) 时域差分法能够很好解决有限周期二维二元周期结构的振动频响曲线的计算;
3) 有限周期结构有较大衰减的频率范围与无限周期结构的弹性波带隙相一致;
4) 周期数越多在无限周期结构的弹性波带隙频率内,弹性波的衰减越明显。
[1] 王矜奉. 固体物理教程[M].济南:山东大学出版社,2004.
[2] KUSHWAHA M S. Giant acoustic stop bands in two-dimensional periodic arrays of liquid cylinders[J]. Appl.Phys. Lett, 1996,69(1): 31-33.
[3] ZHANG Xin, LIU Youyan, et al. Large two-dimensional band gaps in three-component phononic crystals[J]. Physics Letters A, 2003, 317(2):144-149.
[4] WU Fugen, HOU Zhilin, et al. Point defect states in two-dimensional phononic crystals[J]. Physics Letters A, 2001, 292(3): 198-202.
[5] ZHANG Xin, LIU Zhengyou, et al. Elastic wave band gaps for three-dimensional phononic crystals with two structural units[J]. Physics Letters A, 2003, 313(6): 455-460.
