基于小波包—时间序列分析的水位调节器故障诊断方法

1 引 言

传统的信号(如FFT、WDT等)是在频率域中分析信号，它不能给出信号在某个时间上的变换情况，使信号在时间轴上的任何一个突变都会影响信号的整个谱图。而小波包分析可以同时在时域和频域中对信号进行分析，所以它能有效地区分信号中的突变部分和噪声，实现信号的消噪。

经典功率谱估计方法的方差性能较差，分辨率较低。时间序列分析主要是指采用参数模型对所观测到的有序的随机数据进行分析与处理的一种数据处理方法。时间序列分析也称时间序列方法。其最常用的参数模型是AR模型[1]。

2 小波包分析

在Mallat多分辨率分析[2,3]中，由于高频部分的频窗较宽，频率分辨率较低导致许多频率相差很远的频率成分“捆绑”在一起而无法区分，这就是小波变换在高频范围内的低分辨率现象。

20世纪90年代初，通过推广信号的多分辨率分析与正交小波之间的联系， Coifman、Meyer与Wickerhauser引入了小波包。小波包分析能够为信号提供一种更为精细的分析方法，它将频带进行多层次划分，对多分辨率分析没有细分的高频部分进一步分解，从而提高了频率分辨率。图1为一个两层小波包分解树。分解后关系为：s=aa+ad+da+dd。

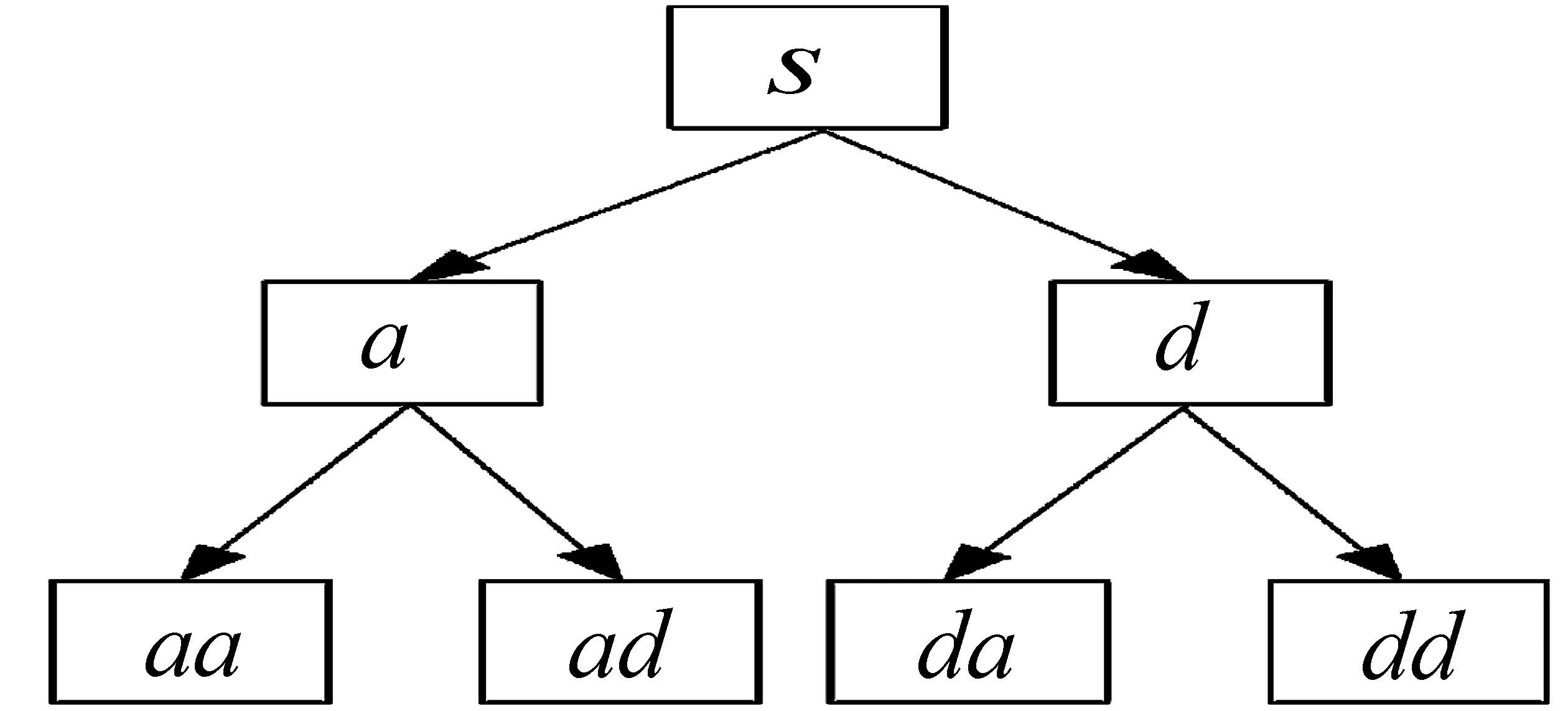
图1 两层小波包分解树

在实际应用中，小波包分解通过下面的递归式实现[4-6]：

(1)

小波包重构递归式：

(2)

小波包分解的实质是让信号通过hk和gk这对高、低通组合滤波器，同时进行二抽一的采样，从而把信号逐层分解到不同的频段上。频段宽度Δf与分解层数j及采样率fs满足如下关系式：

(3)

可见，选择适当的分解层数可以得到所需的频段宽度以及各频段起止频率，从而可以分离原始信号中的有用成分和干扰噪声。

3 基于小波包分解消噪

前面已经提到，小波包相对于小波的主要优点是小波包可以对信号的高频部分做更加细致的刻画，对信号的分析能力更强，因此提出了利用小波包分解进行信号的消噪[7]。应用小波包进行消噪步骤如下：

1) 分解

对信号X采用给定的小波进行N层小波包分解。

2) 计算最佳(优)树

根据给定的熵标准计算初始树的最佳子树。通过Matlab工具可以快速而容易地计算出最佳子树。

3) 对小波包系数进行阈值处理

对每一个小波包系数(除低频部分)，选择一个阈值对其进行阈值处理。如当采用SURE熵标准来选择阈值进行消噪时，设信号长度为l，则阈值s为

(4)

4) 重构

在初始信号第N层低频系数和经过阀值处理后的高频系数的基础上进行小波包重构。

4 随机信号的参数模型

本实验中，采集到的流量信号经小波包分解消噪后成为特征时间序列，可以看作是平稳、零均值的。

对于一个平稳、零均值的时间序列{x(t)},t=1,2,…,N，AR模型如下形式：

(5)

已知AR模型中有a1,a2,…,ap,σ2共p+1个参数。由于自回归参数a1,a2,…,ap反映了系统的固有特性，模型的方差σ2与系统输出特性密切相关。因此，可以用a1,a2,…,ap,σ2这p+1个参数构成判别函数以识别系统的状态。并利用AR模型参数递推估计法中的Burg算法计算出a1,a2,…,ap,σ2。

4．1 AR模型阶次的选取

AR模型阶次升高，则模型逼近真实系统的准确性提高，这是有利的一面。然而，模型阶次升高意味着模型参数增多，则导致计算机误差增大，这又是不利的一面。因此，综合两方面的影响，应该选择一个较为合适的阶次。

本文采用了最终预测误差准则[8](FPE准则)：

式中,N为数据xN(n)长度，当阶次k由1增加时，FPE(k)将在某一个k处取得极小值，将此时的k定为最合适的阶次p。

4.2 模式向量和判别函数的构造

在故障诊断中，系统的不同状态表现出不同的模式，而要进行“识别”即诊断，首先要确定系统的各种参考模式，再将待检模式与参考模式比较，最后确定待检模式属于哪一种参考模式，如图2所示。

图2 模式识别

在应用时序方法时，本文依据AR构造模式向量，借助Euclide距离判别函数，进行模式识别与故障诊断。

4.2.1构造模式向量

由于AR模型中的自回归参数a1,a2,…,ap反映了系统的固有特性，所以可以用这些参数构造成模式识别的模式向量：

ξ=(a1a2…ap)

设系统的某个参考状态对应于参考模式向量ξR：

ξR=(a1Ra2R…apR)

由这种状态的k组数据可以得到k组自回归参数aiR,j(j=1,2,…,k)，由aiR,j排成的矩阵为：

所以参考状态的模式向量[8]为：

4.2.2构造判别函数

式中，j表示第j种待检模式。显然，对一确定的待检模式，它应属于某一参考模式向量的Euclide距离最近的那一个参考状态。

5 小波包—时序方法故障诊断实例

按照上述信号分析方法和故障诊断方法，设计了相应的舰用主冷凝器水位调节系统[9]，进行故障实验。该调节系统设置了4种状态，分别如下：

状态1——调节器正常工作；

状态2——接受喷管被堵；

状态3——测量机构顶针磨损；

状态4——伺服器活塞泄漏。

分别对每种状态进行信号采集，采样频率为100 Hz，采样点数为2 500点，如图3所示。

图3 4种状态下相应的流量信号

从图3中可以看出，4种状态下的流量信号没有有用的特征信息，故分别对这4种状态下所采集到的流量信号进行小波包分解降噪。小波包基函数采用db 4级小波，分解层次为3层。分解降噪的结果如图4所示。

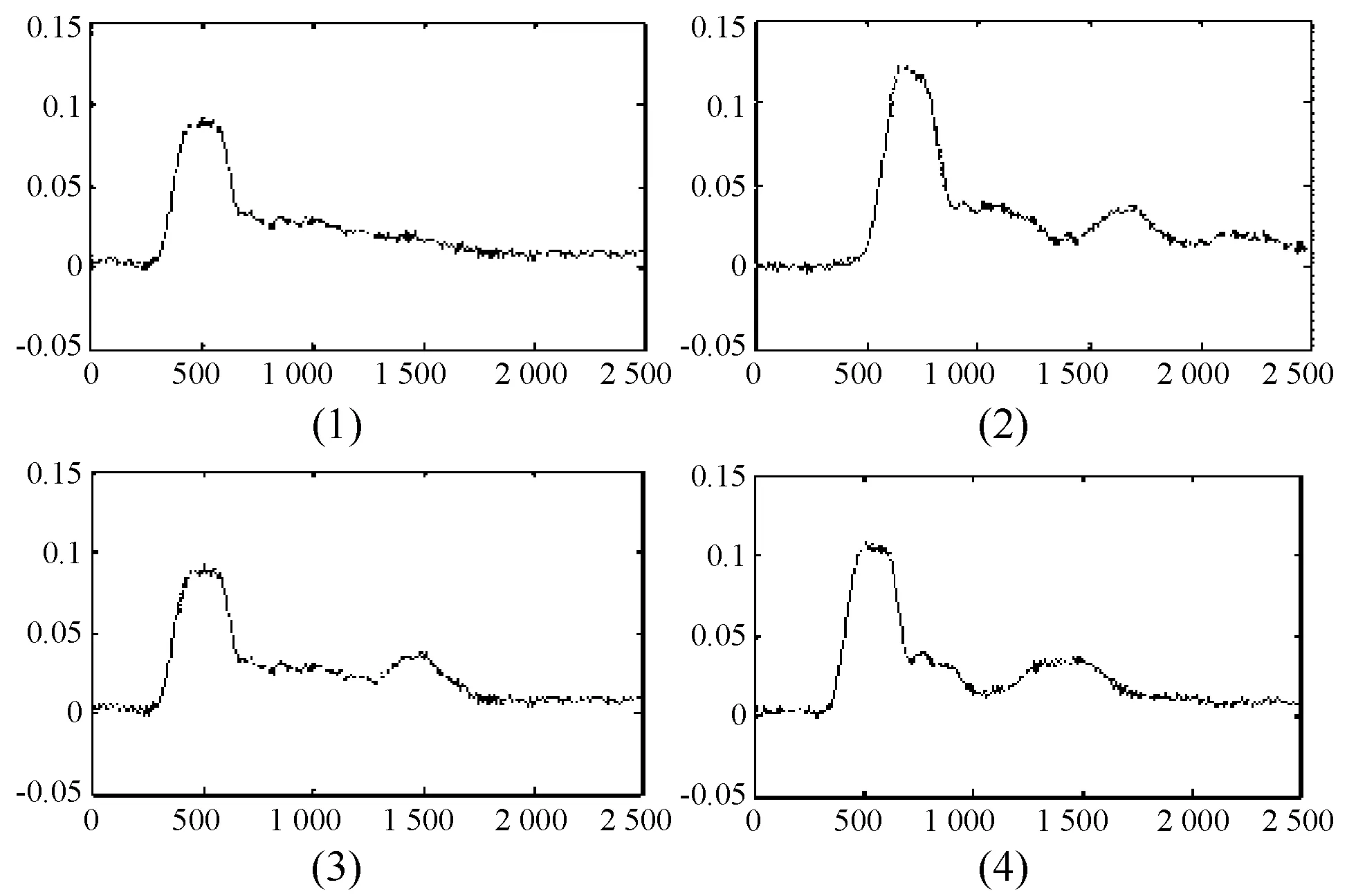
图4 消噪后的流量信号

对于本文实验，取其时间序列模型阶数为6，进行故障诊断时，再取12组调节器工作状态的流量信号，其中正常状态、喷管被堵状态、测量机构顶针磨损和伺服器活塞泄漏状态下各3组，并采用相同的方法对12组信号进行消噪，总共16组信号数据，经过计算得出参考模式向量如表1所示。

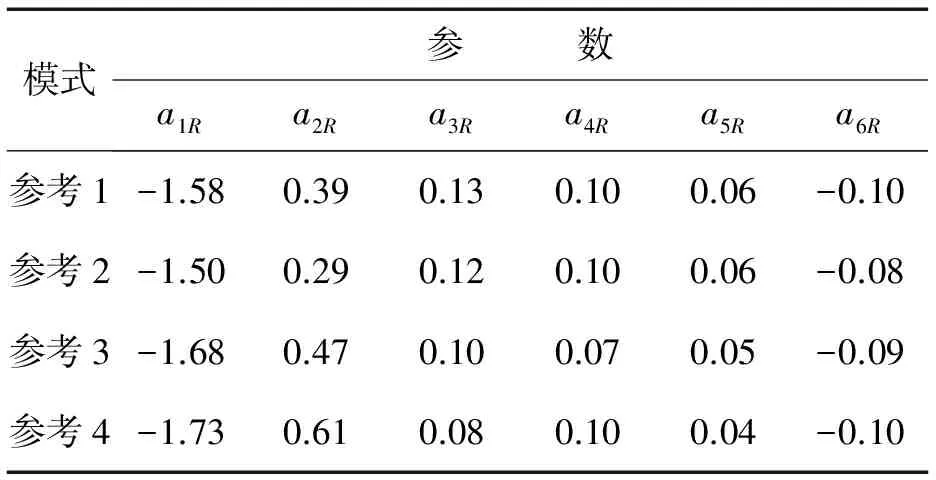
表1 参考模式向量

实验中再取一组待检流量信号，并同样进行小波包分解消噪，结果如图5所示。

图5 待检流量信号

对待检数据进行同样的处理，构造出待检模式向量如表2所示。

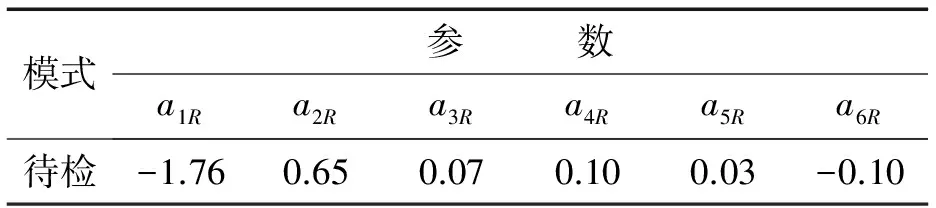
表2 待检模式向量

根据Euclide距离判别函数公式，计算得如表3所示。

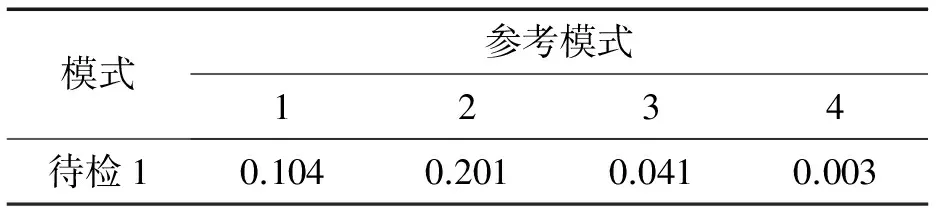
表3 Euclide距离

由表3已知，该待检状态向量与参考模式4(即伺服器活塞泄漏)之间的Euclide距离最小，故判定该待检状态为伺服器活塞泄漏，与实际情况吻合良好。

6 结束语

本文主要是通过主冷凝器水位调节器的实验，采集到各种工作状态下的流量信号，首先利用小波包进行分解消噪，然后再利用时间序列分析方法，通过计算Euclide距离，实验表明该方法可以较好地判断主冷凝器水位调节系统的故障。

实际上，在水位调节系统中任一故障征兆的产生，往往并非单一因素造成的，所以为了更为有效、准确地进行系统的故障诊断，除了流量信号外，在实验中同时可以采集压力信号、振动信号等用来作为辅助诊断。

[1] 胡广书.数字信号处理[M].北京：清华大学出版社，2003.

[2] 罗守华．基于小波分析的液压系统故障研究[D]．南京：东南大学，2003．

[3] 姜万录，张淑清，王益群．液压泵故障的小波变换诊断方法[J]．机械工程学报，2001，37(6)：34-37．

[4] ZBIGNIEW R S. Wavelet methods in (financial) time-series processing[J]. Physica A, 2001(296): 307-319.

[5] 刘威，刘飞，刘丹丹，等．小波变换在时间序列信号长程预测中的应用[J]．黑龙江工程学院学报，2006，20(2)：75-78．

[6] 王国锋，王子良，王太勇，等．Matlab在时间序列分析中的应用[J]．应用科技，2003，30(5)：36-38．

[7] 罗守华，颜景平，王积伟．基于小波包分析的液压系统泄漏故障诊断新方法[J]．制造业自动化，2004，26(3)：70-72．

[8] 刘诗垠.液压元件故障诊断技术研究[D].武汉：武汉理工大学，2001.

[9] 徐基豫,等.汽轮机自动调节[M]. 北京：中国工业出版社,1961.