不同工作状态下增压锅炉的抗冲击特性分析

1 引 言

随着现代水中兵器的发展，水下非接触爆炸对舰船的威胁越来越大。水下爆炸不仅对船体结构威胁，对船用设备的冲击破坏更是一个关系到舰船生命力的问题。船用增压锅炉是船舶蒸汽动力装置中的主要设备，许多学者对其静载下的力学性能进行了研究[1-4]，但是目前并没有考虑水下爆炸的冲击作用，相关的抗冲击分析的资料较少。而在船用锅炉的设计阶段，进行必要的冲击响应数值计算，对提高增压锅炉的抗冲击能力，具有重要的意义。

同时，当增压锅炉处于工作状态，不同空气压力使得结构存在着一定的预应力，此时分析增压锅炉的冲击响应是一个新而复杂的问题。本文采用非线性有限元软件ABAQUS对增压锅炉进行抗冲击数值试验，分析其结构响应，考虑不同工作状态下，内压对增压锅炉的冲击响应影响，以及增压锅炉抗冲击能力极限值的变化规律，从而对增压锅炉抗冲击设计提供参考依据。

2 舰用设备抗冲击分析方法

2.1 设备抗冲击计算方法

舰载设备的冲击理论研究、数学模型、计算方法及冲击仿真研究等在不断发展完善。对设备的抗冲击分析经历了静态等效法、动态设计分析方法和时域模拟法3个阶段。

静态等效法只考虑了受冲击结构的质量效应，当一阶响应是设备的主要破坏因素时尚可用。动态设计分析方法基于动力分析理论，是正则模态响应谱分析法的一种，用于分析舰船设备结构的最大线性动态响应，但只能分析线弹性安装设备与设备线弹性破坏，不能考虑冲击载荷在设备中的瞬态波动效应等；而时域模拟法可采用实测的时间历程曲线，或标准的基础输入时程曲线作为设备的输入载荷，对设备进行瞬态动响应分析，可分析设备的非线性响应。相比之下该方法可以提供更详细的结果，更精确的外部载荷，分析设备的结构属性(如阻尼、非线性、间隙等)更灵活。

为研究舰用增压锅炉在不同工作状态下的冲击响应特性，本文选取时域模拟法对其进行数值冲击试验，以得到更精确的响应信息[5]。

2.2 设备冲击载荷

在进行冲击试验时，增压锅炉受到的冲击载荷可采用实测时间历程曲线，或者标准输入时间历程曲线。当舰船受到水下爆炸冲击时，增压锅炉的基础处会因此得到随时间变化的基础冲击，但其冲击环境极其复杂，实测曲线一般不具备代表性，故本文参照德国军标中的组合三角波法对增压锅炉进行加载[6]。

在该规范中，冲击载荷以设计冲击谱的形式给出，对应于设备的不同安装部位与所受冲击载荷方向，利用简化方法将标准冲击响应谱(SAS)转换成为等效时域加速度曲线。典型的设计冲击谱曲线(图1)由等位移、等速度和等加速度3个曲线组成。最大位移谱为D0，速度谱值为V0，加速度谱值为A0，等速度谱从频率f1～f2。

图1 典型设计冲击谱

按照德国军标的规定，可将用图1所描述的设计冲击谱简化等效为三角形变化历程进行验证计算(图2)，由正负两个三角形脉冲组成。第一个正三角形的加速度峰值，可根据SAS，约为最大加速度的0.6倍。第一个正三角形的面积根据SAS，约为最大速度的3/4。第二个负三角形的面积应与第一个三角形面积大小相同，致使基础最终速度为0。

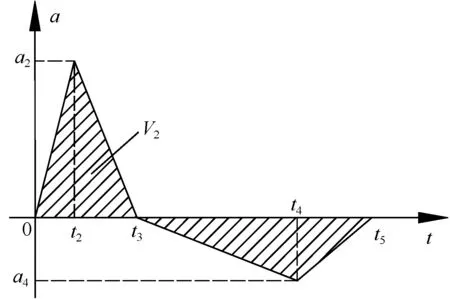
图2 等效加速度时历曲线

此加速度历程的两次积分便得到位移，此位移比SAS的最大相对位移要大1.05倍。另外，选择了t2和t4，使t2=0.4×t3和t4-t3=0.6×(t5-t3)比较合适。上述关系满足下列公式：

a2=0.6·a0

t3=2·V2/a2

a4=-a2t3/(t5-t3)

t4=t3+0.6(t5-t3)

3 增压锅炉数值冲击试验

3.1 增压锅炉有限元模型

增压锅炉几何模型如图3(a)所示。作为薄壳结构，增压锅炉的有限元模型将主要用板壳来模拟。在ABAQUS中模拟冲击和爆炸载荷引起的结构非线性动态响应时，宜选用一阶单元模拟，故用一阶壳单元S3R和S4R对增压锅炉进行网格划分。同时用质量单元MASS模拟某些简化掉的结构惯性作用。划分完毕的增压锅炉有限元模型如图3(b)所示。

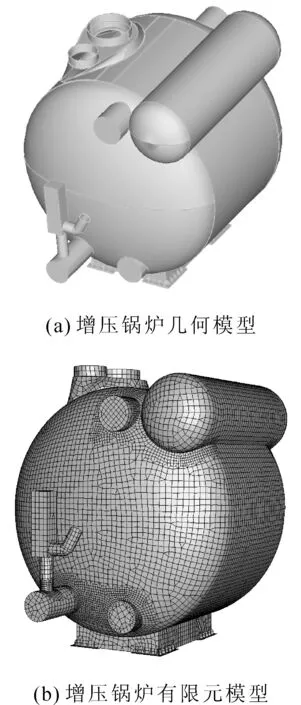
图3 增压锅炉计算模型

3.2 材料模式及失效准则

在空中爆炸等产生高应变率现象的数值试验中，为准确模拟材料在高应变率下的屈服极限提高效应，增压锅炉材料采用PLASTIC-KINEMATICM模式，并考虑材料应变率影响，应变率影响采用Cowper-Symonds模型[7]描述，应变率影响系数为：

该增压锅炉所用具体材料性能：材料密度为7.8×103kg/m3，弹性模量为2.01×1011N/m2，屈服应力为235×106N/m2。

判断设备是否破坏按照德国军标关于A级设备的规定，在已知材料静态屈服极限σs的情况下，求得t时刻的动态屈服应力σ，当σ≥σs时，即认为该A级设备失效破坏，其中动态应力评估是基于Von Mises破坏准则的。而本文所研究的增压锅炉属于A级设备，故采用该方法来评判增压锅炉在冲击载荷下的失效情况。

3.3 工况设置及加载方法

按照上述的冲击输入载荷设置试验工况，为描述方便，第一个正三角波持续时间t3称为脉宽，第一个正三角波峰值a2为加速度峰值。在本文研究中，为定性分析冲击载荷参数对冲击响应的影响，仅分析垂向冲击载荷。表1给出了设计脉宽与加速度峰值，冲击载荷共计5×5=25种。

表1 工况设置列表

同时，本文将考虑设备工作状态对冲击响应的影响。在不同的工作状态下，增压锅炉内外壳之间的空气压力不同，但炉膛内工作压力随工作状态改变，也就是说外壳压力随工作状态改变而内壳承受压力则基本不变。本文计及4种工作状态，对应的内外壳空气压力分别如表2所示。

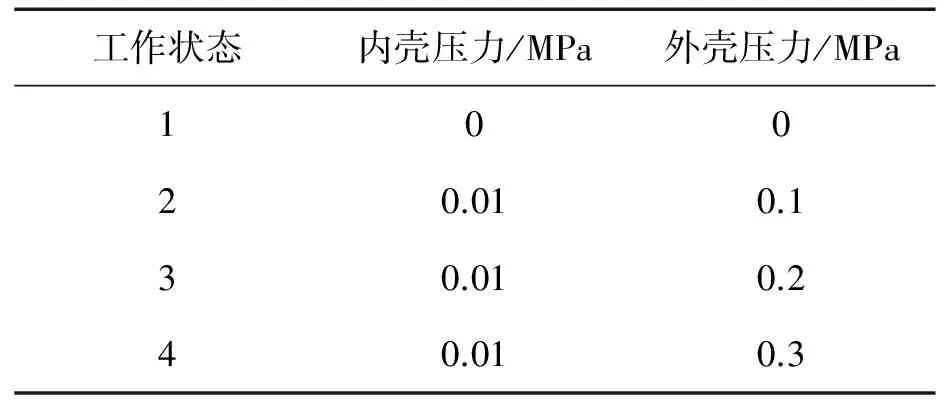
表2 增压锅炉工作状态

在进行冲击计算时，将不同工作状态与冲击载荷组合进行加载，则工况将共计4×25=100种。

根据实际情况，增压锅炉与设备基座之间无弹性抗冲装置，故在抗冲击计算中认为刚性边界条件，冲击加速度载荷将直接施加于底座。当考虑工作状态的空气压力时，即当设备在承受空气压力作用的基础上进行冲击载荷的加载。

4 工作状态的预应力分析

在工作状态下，增压锅炉受到空气内压作用产生一定预应力，可以看作静力问题，一般可以用隐式求解器分析。而后受到冲击载荷作用的结构瞬态、非线性响应则须用显式动力求解器分析。对于本文分析的不同工作状态下设备的冲击动响应问题，尽管该问题可以联合隐式分析和显式分析进行多步骤求解，但在ABAQUS中两种分析模式的接口不是无缝的，单元类型不通用可能导致过多的用户干预，将不便于工程应用。

为高效、方便地分析这个问题，本文用大阻尼显式方法进行处理[8]，即采用的两步计算载荷，都用显式方法求解。第一步引入动态振荡阻尼使增压锅炉在空气压力作用下尽快达到平衡；第二步去掉动态振荡阻尼，加载冲击载荷。

图4给出了在4种工作状态下增压锅炉内壳的预应力平衡云图。内壳在空气压力作用下整体的应力分布不均匀，内壳与上下集箱、上锅筒等具有较厚的圆柱壳相交的部位，以及内壳尖角部位压力产生的预应力较大，存在应力集中现象，而其余部位应力较小。外壳由于厚度较大，在空气压力作用下应力相对较小，且应力集中没有内壳明显。

图4 工作状态4下内壳预应力云图

为给出采用隐式方法与显式方法分析增压锅炉在工作状态4的内压作用下的预应力对比，表3列出了增压锅炉内、外壳某部位分别的Von. Mises应力以及位移量。两者计算的结果偏差在0.7%以内，可见两种方法得到增压锅炉的预应力相差很小，故采用显式方法加动态振荡阻尼求解静力问题是可信的。

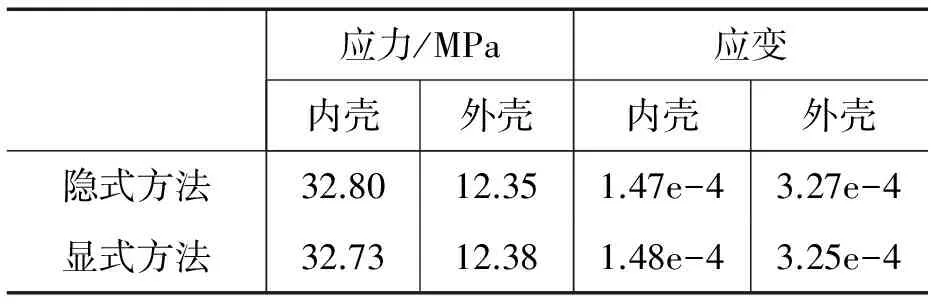
表3 隐式方法和显式方法求解结果对比

在施加适当的阻尼后，在最短的时间内使增压锅炉在内压作用下达到平衡，在此基础之上再进行冲击响应分析：去掉在第一步载荷中施加的阻尼，此时增压锅炉将同时受到空气压力载荷和冲击载荷的作用。取增压锅炉外壳单元的整个分析过程Mises应力响应曲线如图5所示。可见，在适当阻尼的作用下，增压锅炉迅速达到平衡，几乎没有经过振荡，且冲击响应是在预应力基础上发生的，整个过程兼容无缝。

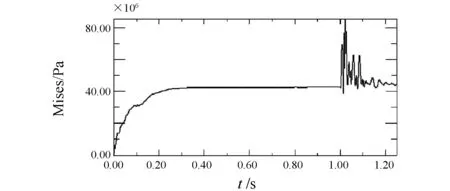
图5 外壳单元在整个过程中的Mises应力时历曲线

5 数值试验结果分析

5.1 结构响应随冲击载荷参数的变化规律

为了寻找增压锅炉冲击响应随着载荷参数的变化规律，除了利用无量纲系数n之外，需要将应力及载荷参数、加速度、脉宽进行无量纲化，具体方法如下：

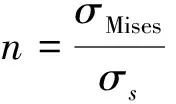
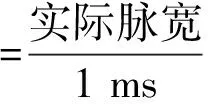
式中，σMises为考核部位单元Mises应力峰值，MPa；σs为材料静态屈服极限，MPa。

为分析结构响应随加速度变化规律，图6、图7给出了工作状态1以及工作状态4下，内外壳某两考核点在脉宽为10 ms下的冲击响应随加速度峰值变化规律，其中纵轴为Mises应力失效系数n，横轴分别为无量纲加速度峰值。

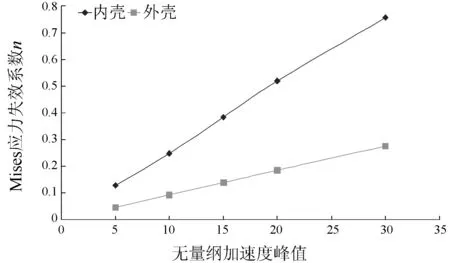
图6 工作状态1的Mises应力失效系数n与无量纲加速度峰值的关系曲线

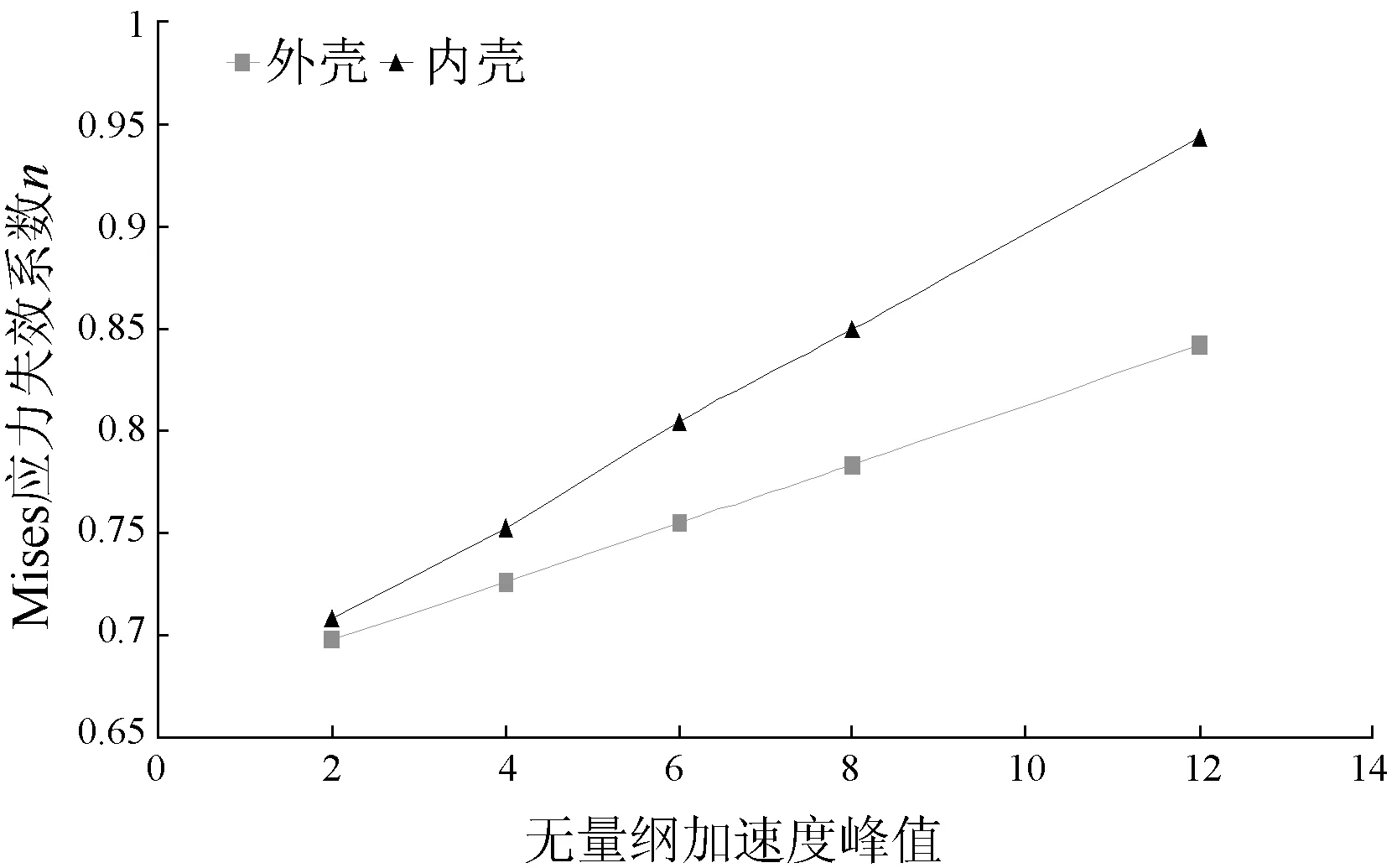
图7 工作状态4下的Mises应力失效系数n与无量纲加速度峰值的关系曲线

可以看出，即使在不同的工作状态下，无论对外壳还是内壳，保持冲击载荷的脉宽不变，增加加速度峰值，内外壳考核单元的响应程度基本上呈线性增长趋势。

为分析结构响应随脉宽变化趋势，图8、图9给出了工作状态1及工作状态4下，内外壳冲击响应在加速度峰值为15 g情况下随纲脉宽的变化规律，其中纵轴为Mises应力失效系数n，横轴为无量纲脉宽。

图8 工作状态1下的Mises应力失效系数n与无量纲脉宽的关系曲线

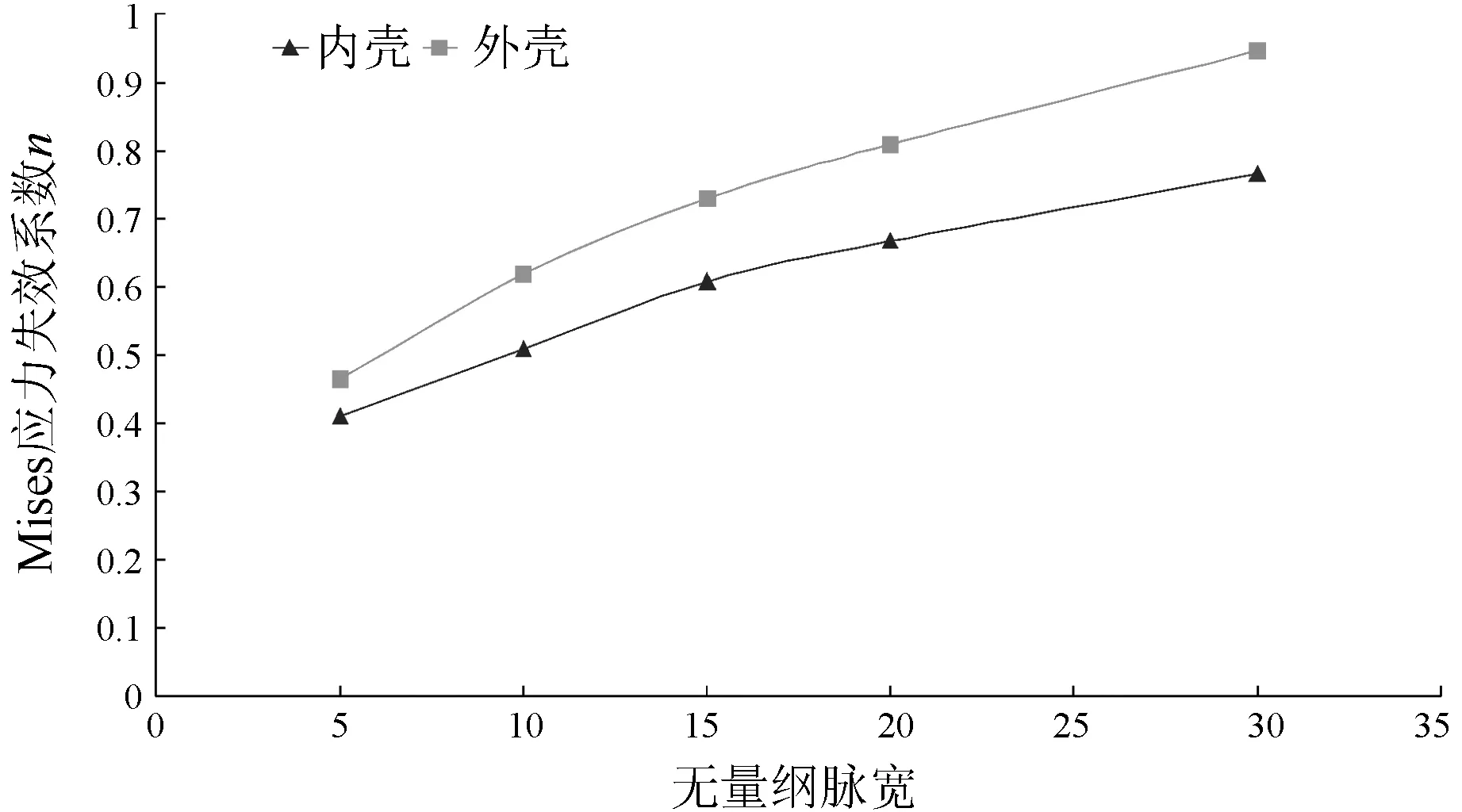
图9 工作状态4下的Mises应力失效系数n与无量纲脉宽的关系曲线

在不计内压时，若保持加速度峰值不变，增加载荷脉宽，内外壳响应增加，并且冲击载荷脉宽值小于15 ms之前，结构响应对脉宽变化敏感，冲击响应随脉宽呈线性增加，脉宽在15 ms与20 ms之间是过渡阶段，当脉宽大于20 ms之后，结构响应对脉宽变化不敏感，增加脉宽，结构响应增加幅度较小。而当计及内压后，内外壳冲击响应随着脉宽均匀增加。

5.2 冲击响应随工作状态的变化规律

由于增压锅炉结构预应力的存在，结构的刚度会随之发生变化，结构的冲击响应会受到影响。图10～图13给出了在10 ms、15 g冲击作用下，同一时刻增压锅炉内壳的响应云图。

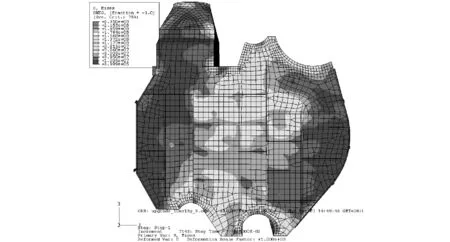
图10 工作状态1下内壳冲击响应应力云图

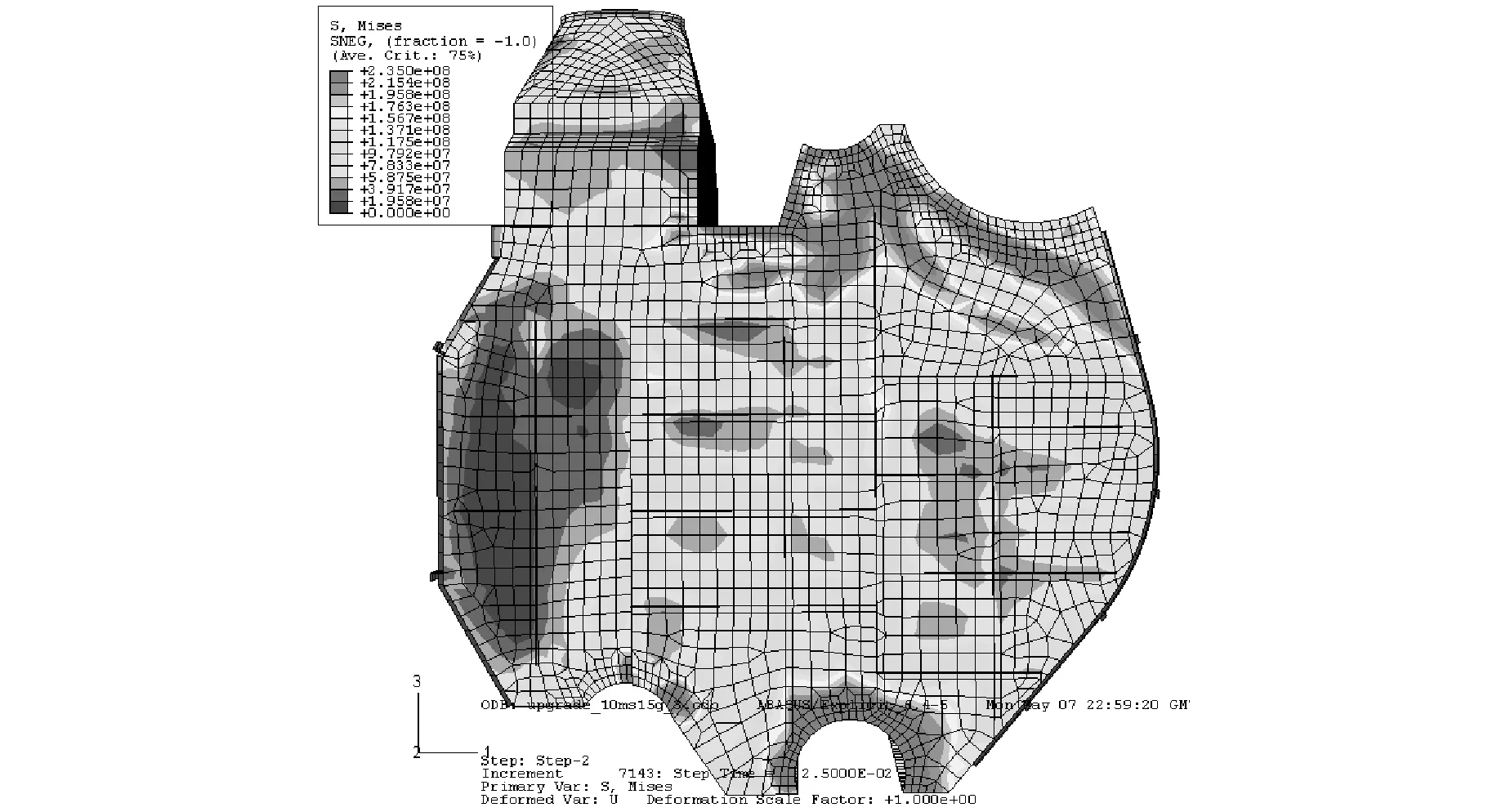
图11 工作状态2下内壳冲击响应应力云图

图12 工作状态3下内壳冲击响应应力云图

图13 工作状态4下内壳冲击响应应力云图

可以看到，工作状态1下的响应最小，其余工作状态下响应都比较剧烈，并且应力分布范围比较相似。增压锅炉的应力值比较大的部位主要出现在内、外壳与具有较大厚度的圆柱体相交处，即与上锅筒、集箱相交的部位。危险的部位较多存在内壳。

为说明压力作用对冲击响应的影响，图14、图15选取了位于内壳上的某一考核单元的在不同工作状态下Mises应力响应，其中横轴为Mises应力，纵轴为时间。

图14 不计内压时某考核单元冲击阶段应力时历曲线

图15 不同内压时某考核单元冲击阶段应力时历曲线

空气压力在增压锅炉冲击响应中起到了阻尼的作用，使得其结构振荡受到阻滞[9]，增压锅炉振动的能量随时间损耗，响应也由于这种空气静压的阻尼作用衰减。对比该考核单元在不同工作状态下的响应，发现考虑内压后，不同工作状态下结构的Mises应力响应比较相似，随时间变化趋势比较一致，并且衰减项对于无内压时变化更快。

经过分析，发现内外壳上都存在着压力敏感部位与压力非敏感部位。压力敏感部位分布于增压锅炉结构应力集中部位，如内壳与集箱、锅筒相交位置及内壳尖角，在冲击作用下该部位处响应较无内压时剧增；压力非敏感部位在受到冲击作用时，内压所起到的阻尼作用在一定程度上将冲击响应峰值降低，导致其响应较无内压时增长很小，甚至减小。

于是本文在外壳、内壳的压力敏感部位与压力非敏感部位分别选取考核点。图16～图19分别给出了同样冲击载荷下这些考核点的冲击响应随压力值的变化曲线。横轴为无量纲压力，纵轴为失效系数n，其中：

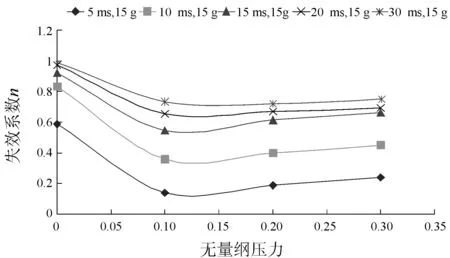
图16 外壳压力非敏感部位的冲击响应随压力变化曲线

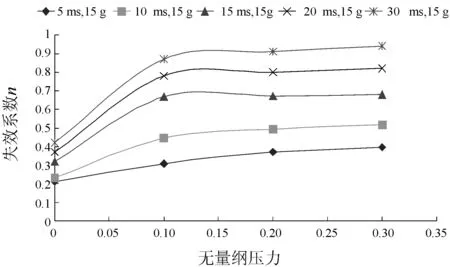
图17 外壳压力敏感部位的冲击响应随压力变化曲线

图18 内壳压力非敏感部位的冲击响应随压力变化曲线

图19 内壳压力敏感部位的冲击响应随压力变化曲线

从图中可以发现，不同冲击载荷作用下，对于压力非敏感部位，当内压从0 MPa变为0.1 MPa，冲击响应值变小，对于压力敏感部位，冲击响应则增大。当从0.1 MPa增长至0.3 MPa，各部位响应都随压力增大而增大。可见，对于增压锅炉的压力非敏感部位，空气压力的阻尼作用能够提高该部位的抗冲击能力，而对于增压锅炉的压力敏感部位,大大降低了该部位的抗冲击能力。

而增压锅炉的压力敏感部位位于外壳与集箱、底座相交处，内壳尖角、内壳与上下集箱、上锅筒相交的地方，而这些位置也是在冲击作用下应力较大的地方，压力作用使得该处的冲击响应急剧变大，则可知压力对结构整体的抗冲击能力是有削弱作用的。

5.3 增压锅炉极限抗冲击能力变化规律

根据有关规范对于增压锅炉该级设备的相关规定为：由冲击载荷引起的应力不得超过静态屈服极限(若动态应力提高出现安全值，可以提高屈服极限),则增压锅炉抗冲击能力极限值是指该设备所能承受的最大冲击载荷而不产生破坏的载荷值。

按照上述规定，对上述工况分析得到不同脉宽下的增压锅炉抗冲击极限值，并进行无量纲化，可得到图20所示的极限值随脉宽变化的规律，其中横轴为脉宽，纵轴为无量纲加速度峰值。

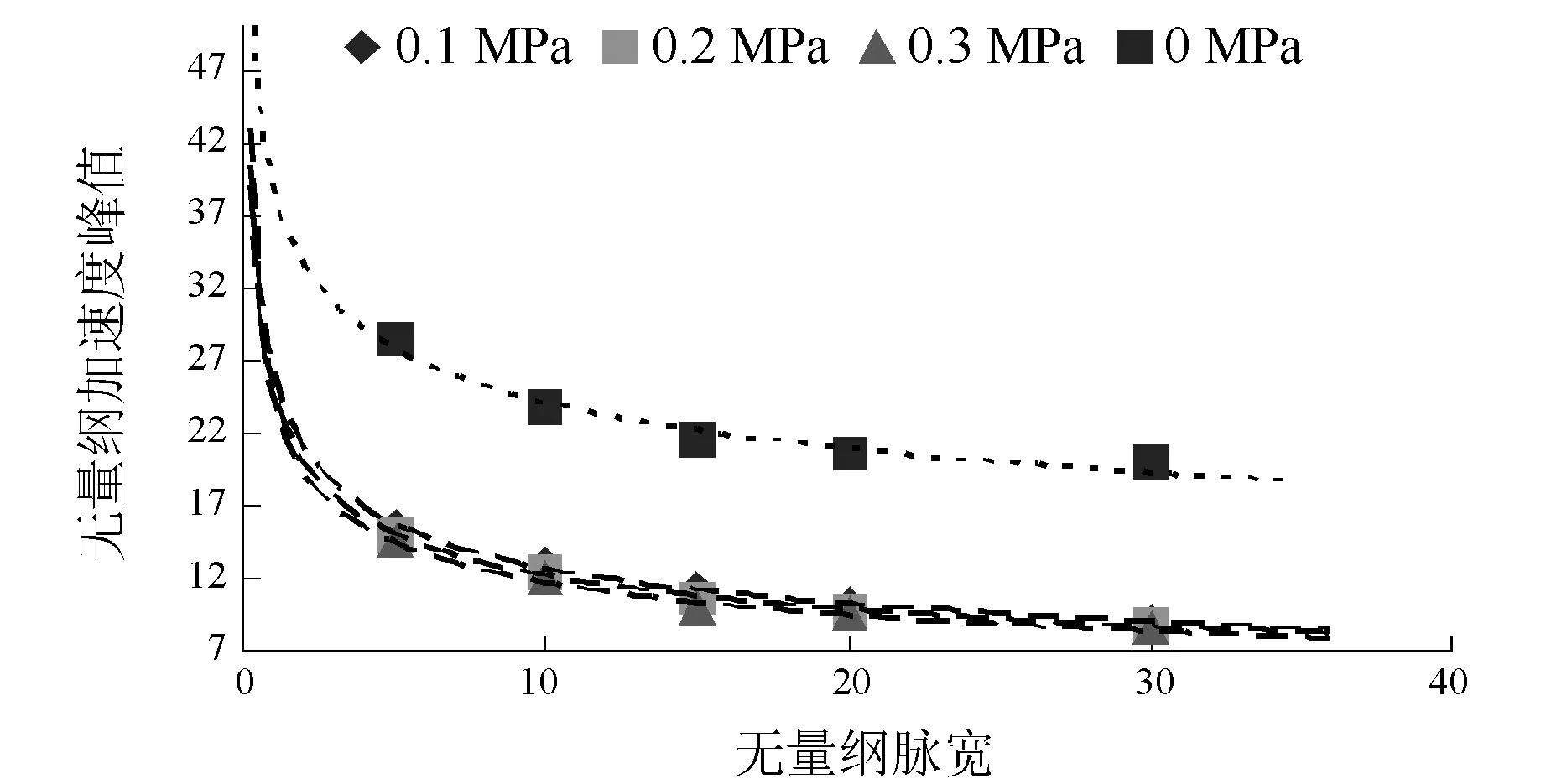
图20 不同工作状态下增压锅炉抗冲击极限值随脉宽变化规律

在各个工作状态下增压锅炉抗冲击加速度峰值，随着冲击载荷脉宽的增加而增加。当脉宽趋于∞时抗冲击加速度峰值趋于0；当脉宽很小时，抗冲击加速度峰值趋于∞，这也与上文中分析增压锅炉的抗冲击特性相吻合。

计及工作内压之后，增压锅炉的抗冲击极限值有了明显的降低，这说明工作压力对结构的抗冲击能力有削弱作用。在以后的锅炉抗冲击设计中应该对压力敏感部位进行优化设计，降低该处在压力作用下的应力集中现象，从而可以大幅提高结构的抗冲击能力。

抗冲击加速度峰值随脉宽的变化趋势线，相当于设备抗冲击安全限值曲线，低于该曲线的冲击值不会对设备造成破坏。

6 结 论

文中按照相关标准中的载荷设置方法，采用ABAQUS对增压锅炉在不同工作状态下进行了时域冲击计算，并得到了一些有益的结论。

1) 由于预应力的存在，增压锅炉结构在空气压力作用下，冲击响应与不计内压有很大不同，空气压力的阻尼作用使得结构响应迅速衰减；

2) 不同的工作状态，即本文中不同内压的作用， 对于增压锅炉不同部位的抗冲击影响是不同的。对于压力非敏感部位，内压提高结构抗冲击能力越大；而对于压力敏感部位，内压降低结构的抗冲击能力越弱。由于压力敏感部位多位于抗冲击薄弱环节，也就是说工作内压削弱了增压锅炉的抗冲击能力；

3) 不同工作状态下锅炉的抗冲击极限加速度峰值随着载荷脉宽增加而降低，脉宽越小，抗冲击加速度峰值越大，反之亦然；

4) 在将来的增压锅炉抗冲击设计中，可对压力敏感部位进行优化，从而提高在工作状态下的增压锅炉抗冲击极限能力。

[1] SPENCE J, NASH D H. Milestones in pressure vessel technology [J]. International Journal of Pressure Vessels and Piping, 2004,81(2):89-118.

[2] HOLLINGER G, HECHMER J. Three-dimensional stress criteria-summary of the PVRC project [J]. Journal of Pressure Vessel Technology, 2000,122(1): 105-109.

[3] 赵在理.压力容器的结构分析与安全评估研究[D].武汉：武汉理工大学，2006.

[4] 梅林涛，杨国义，寿比南.有限元在压力容器设计中的应用现状和展望[G]. ABAQUS 2004年度用户大会论文集，2004.

[5] THOMAS L, CARTER. Correlation of the DDAM and transient shock analysis methods using the MK 45 LFSP shock test results[G]. Shock and vibration bulletin,1989.

[6] BV0430-85德国国防军舰建造规范-冲击安全性[S],2004.

[7] 王儒策，赵国志主编.弹丸终点效应[M].北京：北京理工大学出版社，1993.

[8] 张阿漫.水下爆炸载荷作用下的船体总强度计算方法研究[D].哈尔滨：哈尔滨工程大学,2006.

[9] 姚熊亮.舰船结构振动冲击与噪声[M].北京：国防工业出版社， 2007.