典型舰船舱室大气环境仿真
2008-04-24曹红波,谢伟
1 引 言
目前在舰船舱室大气环境设计中,安装有大功率发热设备和动力设备的重要舱室由于设备布置密集,在通风调节的过程中,极可能形成局部区域温度、压力梯度较大等设计不足,从而造成局部通风效果较差,不能达到所要求的舱内大气环境。为解决以上设计中出现的问题,传统的射流理论可以简单、快捷地预测机械通风室内沿射流方向各个位置的速度或温度分布,从而了解室内空气分布情况。但是用射流公式预测室内空气分布有很大的局限性,依赖于确定射流公式的经验参数。另外,射流公式揭示的多为射流主体段的流动特性,对于送风口相对空间尺寸较大、送风射流不能充分发展的情形,如果仍采用射流理论分析,势必带来较大的误差,使射流公式预测的结果可信度偏低。并且,射流理论分析方法只能给出室内的一些集总参数(即平均参数)性的信息,不能给出流场分布所需的详细资料。随着数值计算技术的发展,利用计算流体力学(CFD)技术对各种流场进行仿真是近年来普遍采用的一种新的方法,该方法在船舶工程领域也得到越来越多的应用。借助CFD数值模拟,设计人员可以对气流流场进行形象化图形演示,显示出温度场、压力场、速度场等详细的分布,可以形象直观地为设计人员提供理论依据,帮助工程设计人员进行优化设计,提高工程设计质量,节省实验所需的人力、物力和时间。针对典型舰船舱室大气环境系统的优化,本文考虑用CFX软件对典型舰船舱室大气环境进行仿真,将数字仿真技术与舰船舱室大气环境系统相结合,初步探索一种提高舱室大气环境系统设计的方法。
2 典型舰船舱室大气环境仿真及对比
2.1 数学模型
2.1.1模拟过程中的假设
1) 典型舰船舱室内气流流动为紊态流动;
2) 舱室气体是低速不可压缩牛顿流体,作定常流动;
3) 忽略能量方程中由于粘性作用所引起的能量耗散;
4) 舱室内热源均匀,表面温度为定值。
2.1.2 RNGk-ε模型
本文仿真的典型舱室属于高Re数的湍流流动,所以选择RNGk-ε模型,它是由YAKHOT及ORZAG[1]提出的,该模型中的RNG是英文“Renormalization group”的缩写,译为“重正化群”。在RNGk-ε模型中,通过在大尺度运动和修正后的粘度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除[2]。该仿真包含的控制方程如下:
连续性方程:
(1)
动量方程:
(2)
(3)
(4)
能量方程:
(5)
湍动能k方程:
+Gk-ρε
(6)
湍动耗散率ε方程:
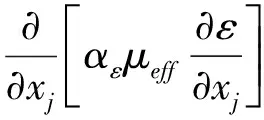
(7)
2.2 物理模型简化
典型舰船舱室大气环境仿真选择的对象是动力机舱。下面是对模型进行简化处理的介绍:
1) 壁面的肋骨、加强结构等不进行建模处理,并将舱壁处理成光滑的壁面结构。
2) 复杂的曲面船体采用近似的圆弧型壁面代替,减少建模的难度。
3) 对舱室内的小构件、小发热体等不作建模处理,突出仿真建模的主要方面,忽略次要方面。
4) 动力机舱较大,且舱内设备布置基本对称,为便于仿真建模及计算,只对动力机舱的一半(即右舷部分)进行建模仿真计算。
5) 舱内设备用近似的长方体或圆柱等来代替其外形轮廓,为利于网格的划分,将代表大设备的长方体边缘进行倒圆角处理。
6) 动力机舱的进/回风管路、进风口等也较多较复杂,为了仿真计算的准确性,将风管及风口也在模型中建立起来。
建模后的物理模型及进出风口如图1所示。

图1 动力机舱物理模型及进出风口图
2.3 进出口模型
2.3.1动量方法
1991年,陈清焰提出了用动量方法描述风口入流边界条件[3]。动量方法用一个与原风口或散流器外形相同的矩形开口代替该风口或散流器,而将入口动量置为实际的空气入口动量Jm,定义如下:
(8)
式中,vr为实际入流速度,L为实际入流风量,Ae为风口有效面积,A为风口外形总面积,f为风口有效面积和外形总面积之比,称为有效面积系数,反映了风口或散流器有质量流入的面积(开口面积)占其外形总面积的比例,它可作为表征风口或散流器的面积出流特征的一个参数。藉此,动量方法可理解为“基本模型[4]”的极端:即用无数个“小的”矩形开口来代替实际的风口或散流器。
2.3.2仿真中丝网风口的处理
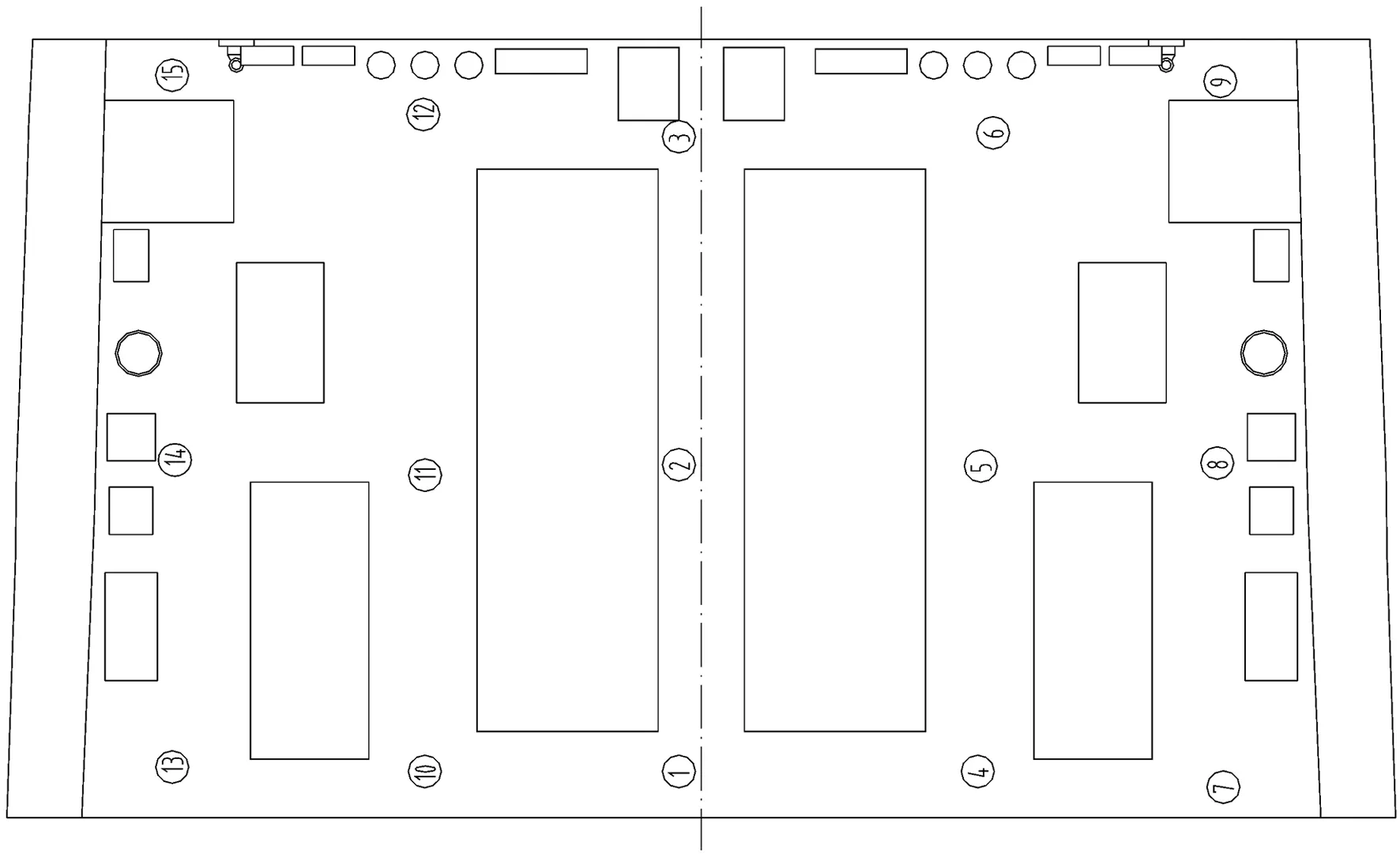
所建模型中的进、出风口由间距为10 mm×10 mm,直径为1 mm的金属丝网构成。进出风口丝网有效面积计算如图2所示。

图2 金属丝网有效面积计算示意图
有效面积系数f计算式:
(9)
按照风口的动量模型方法,各风口的风口面积、有效面积和风口速度见表1。

表1 各风口面积、有效面积及理论风速
2.4 物理边界条件设置
2.4.1壁面函数
壁面函数法实际是一组半经验公式,它将壁面上的物理量与湍流核心区内待求的未知量直接联系起来,与高Re数k-ε模型配合使用能达到较理想的效果。
当y+<5时,所对应的区域是粘性底层,这时速度沿壁面法线方向呈线性分布,即:
u+=y+
(10)
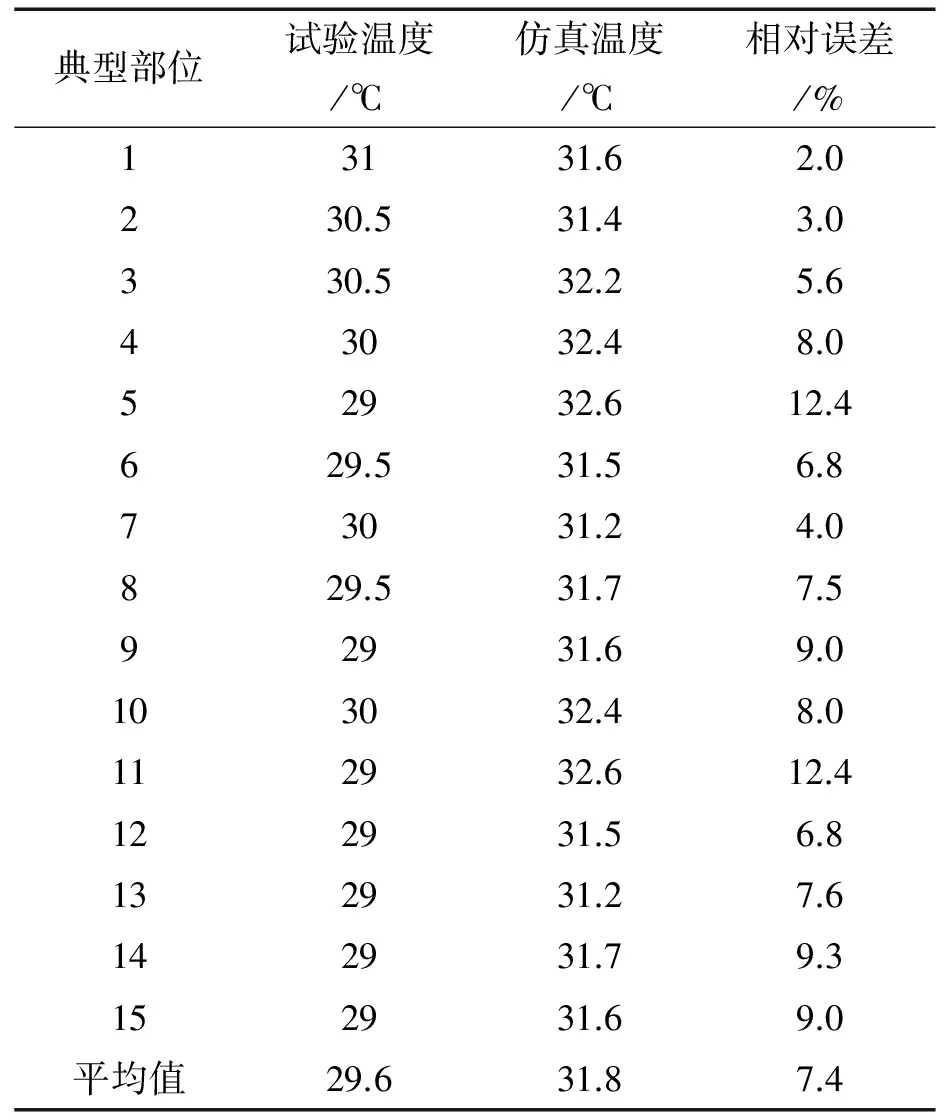
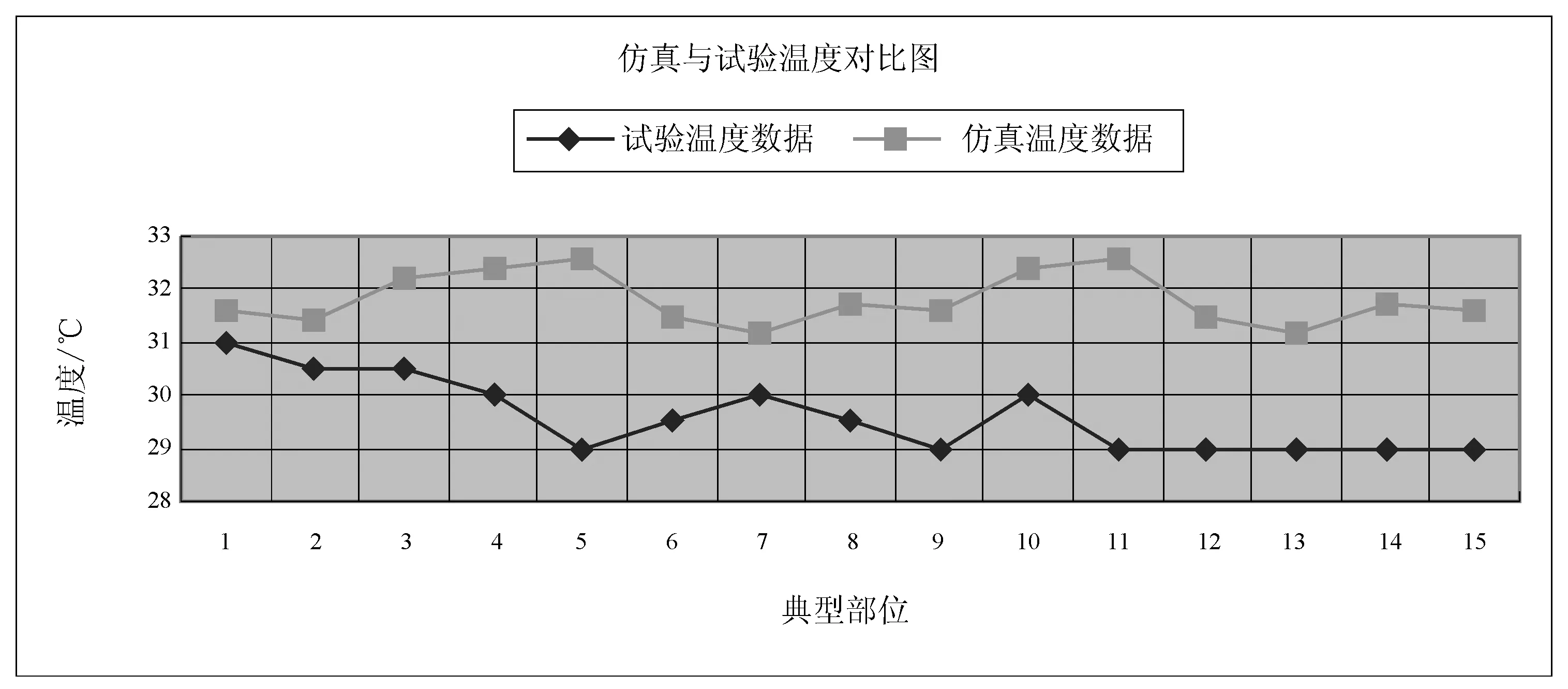
当60 (11) 式中,κ为Karman常数;B和E是与表面粗糙度有关的常数,对于光滑壁面有κ=0.4,B=5.5,E=9.8。文献[5]推荐将y+=11.63作为粘性底层与对数律层的分界点。 2.4.2进、出风口边界 进风口边界按表1所列的进风速度取值作为输入边界条件。 κ值按文献[5]取来流进口的0.5%~1.5%计算,入口截面上的ε则可按下式计算: ε=Cμρk2/μt (12) 式中, 常数Cμ=0.09。 入口处μt按下式估算: ρuL/μt=100~1 000 (13) 出口处的边界取为出口流量L=1.975 kg/s。 2.4.3固体壁面 仿真后的结果经过可视化处理,取Z=0.5 m处的平面温度等值线、面图如图3所示。舰船试验时,动力机舱典型部位测量点如图4所示。 图3 Z=0.5 m处平面温度等值线、面分布图 图4 典型部位温度测点位置示意图 在正常工况下,外界环境温度为31 ℃,湿度为83%时,动力机舱大气环境系统运行1小时,舱室环境达到稳定后,试验测点温度值与仿真测点温度值如表2所示。其中,试验测点温度值来自试验记录表,仿真测点温度值来自图3中相应典型部位的等值线、面的温度值。 表2 试验测点温度与仿真测点温度对比表 为便于分析比较,将表2转化成图5典型部位测点温度对比图的形式。 图5 试验测点温度与仿真测点温度对比图 图5中各测点处的仿真温度值均大于试验温度值,原因在于:仿真中,舱内设备外表面均设为不工作时的初始环境温度t=31 ℃,在仿真的过程中,该固定表面温度成为热源不断地向舱室散发热量,导致仿真测点处温度普遍升高。从图5温度对比中可以看出,仿真的温度场值大致反映了典型舱室大气环境的运动趋势,其中,大部分的温度误差在10%左右。由此推之,在对仿真对象进行细致的建模,并对其网格进行细化之后,仿真的结果可以达到工程实际应用所需的要求。 在仿真结果处理时,利用流线处理进风口1的出风路线时发现:靠近出风口处的进风口1出现了空气短路现象。原因在于:出风口处的风量较大,出风速度很大,由伯努利原理可知该处压力较低,进风口1距离出风口近,导致进风后直接流向出风口。该现象不利于能量的充分利用,并造成空气组织不合理分布,在设计中应尽量避免。图6显示了进风口1的流向出风口的出风路线图。 图6 进风口1的短路现象 本文对典型舰船舱室大气环境的温度场进行了仿真,并提取了该舱室典型部位的仿真温度场数据,将其与试验数据进行了对比分析,分析结果表明:仿真的结果与试验的结果之间的相对误差≤12.4%,仿真结果和实验结果比较吻合。同时,通过仿真的流线显示了离出风口较近的风口送风短路的现象。因此,由以上结论可知,典型舰船舱室大气环境仿真验证了舱室大气环境流动趋势的正确性和参与工程实际设计的可行性,从而为设计和校验舰船舱室大气环境系统找到了一条可行的数值化途径。 [1] YAKHOT V,ORZAG S A.Renormalization group analysis of turbulence:basic theory[J].J Scient Comput,1986,1:3-11. [2] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004. [3] CHEN Q,MOSER A. Simulation of a multiple-nozzle difuser. Proceedings of the 12th AfVC Conference on Air Movement and Ventilation Control Within Buildings, Vol. 2[C].The IEAAir Infiltration and Ventilation Center, Ottawa, Canada, Semptember,1991. [4] 章梓雄,董曾南.粘性流体力学[M].北京:清华大学出版社,1998. [5] 陶文铨.数值传热学(第二版)[M].西安:西安交通大学出版社,2001.
3 结果对比分析与讨论
3.1 仿真温度图数据处理

3.2 典型温度对比
3.3 气流短路现象分析

4 结 论
