结合均值导纳法的声呐腔自噪声统计能量分析
2008-04-24张娟,严谨,吴光林
1 引 言
统计能量分析方法(SEA)的核心是统计能量分析参数(模态密度、耦合损耗因子以及内损耗因子)的确定。一直以来,耦合损耗因子的计算都是依赖于以保守弱耦合为基础的经验公式。在复杂结构声和振动响应预测中的应用受到限制。利用均值导纳法预测结构间的振动响应可以克服经典统计能量分析关于模态密度和弱耦合假设引起的缺陷,从而扩大统计能量分析法的应用范围,提高统计能量分析的预测精度。
孙进才[1-3]等人在这方面做了大量的工作,利用均值导纳法推导了点连接结构、线连接结构耦合损耗因子的计算公式。本文在此基础上,利用均值导纳法推导湍流边界层激励下复杂结构—声耦合系统——板—柱壳—板—声呐腔的耦合损耗因子,预测声呐腔的自噪声。
2 声呐罩统计能量分析模型
俞孟萨[4,5]等人对均匀湍流边界层激励声呐罩模型进行了分析。本文采用的声呐罩模型为两端封闭的圆柱壳模型。圆柱壳半径为R,长为L,厚度为hs,两端圆形封板半径为R,厚度为hp,两者密度均为ρ。相应的统计能量分析模型如图1所示。此模型的能量平衡方程为:

(1)
式中,ηit=ηi1+ηi2+ηi3(i=1,2,3)。
确定了所有的参数后,根据式(1)求出E2,再根据下式即可计算得到声呐腔的自噪声:
(2)

图1 声呐罩统计能量分析模型
式中,pi、ρ0、C0、Vi分别为声子系统均方根声压、介质密度、声速、体积。
3 统计能量分析参数的确定
1) 模态密度
柱壳的环频率为:
fr=Cl/(2πR)
(3)
式中,Cl为柱壳材料中的纵波速。
柱壳的模态密度为[5]:
(4)
式中,A为圆柱壳表面积。
壳内声场的模态密度[5]近似计算公式为:
(5)
式中,V0为声场的体积;Aa为声场的表面积。
圆板的弯曲模态密度为:
n4(ω)=0.5Ap(m/D)0.5=n3(ω)
(6)
式中,Ap=πR2为板的面积;m=ρhp为板面密度;D为板弯曲刚度。弹性壳体在受流体负载作用后,其模态频率会向低频移动,相应的模态密度也会产生变化。Blake给出了有流体负载的平板的模态密度,其表达式为:
n4(ω)=0.5A3(mL/D)0.5/a
(7)

2) 内损耗因子
根据文献[6],组合结构中1个结构子系统的内损耗因子是由3个部分组成的:结构损耗因子、连接边界损耗因子、声辐射损耗因子。在给定频率,结构损耗因子仅与材料有关。结构损耗因子的数量级为10-3~10-4。连接边界损耗因子则与连接的形式有关。连接形式的不同而导致的声压级的差异通常在0~3 dB。因此,此处不具体计算连接边界损耗因子,而是在最终的声压级计算结果上加上修正值。结构的声辐射为双面声辐射。因此有:
η1=η1s+η1r,η3=η3s+η3r,η4=η4s+η4r
(8)
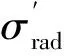
声场的内损耗因子可从声场的混响时间T60得到[6]:
(9)
式中α,Af分别为非透声界面的吸声系数、非透声界面的面积。
3) 耦合损耗因子
本文利用均值导纳法计算圆板—柱—圆板耦合损耗因子。其计算矩阵如下:
(10)

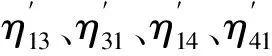
(11)
式中,Y1、Y4、Y3分别为子系统1、3、4的平均输入导纳,y1、y3分别为子系统1、3的平均传递导纳。且据文献[7]有:
(12)
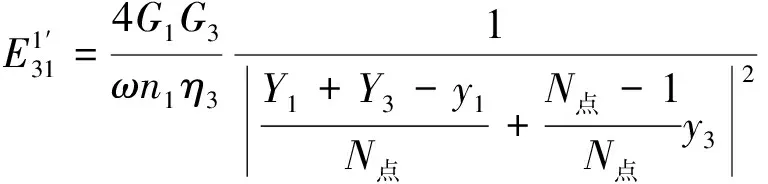

利用式(12)求得经典耦合损耗因子,然后代入式(11)求得振动能量比,将所得各数值代入式(10)中,即可得结构子系统间的直接耦合损耗因子和间接耦合损耗因子。
4) 输入功率
声呐罩一般为水翼截面的柱壳,本文为便于讨论采用圆截面柱壳。仅圆柱壳均受到湍流边界层脉动压力激励。湍流边界层脉动压力为空间分布的随机力。如图2所示,平行于组合结构对称轴的无穷远处均匀来流流经结构表面,在结构表面形成湍流边界层。

图2 声呐罩物理模型
柱壳表面两点X(x1,θ1)、X′(x2,θ2)。利用导纳法计算输入功率。Han研究了导纳与输入功率的关系。稍做推导,得出均布随机脉动压力对柱壳的输入功率的计算公式:
ds
(13)
式中,Sxx′(ω)为柱壳表面压力互谱密度函数;Mpxx′*(ω)为柱壳的传递导纳函数Mpxx′(ω)的共轭;s1为柱壳的面积。
SXX′=φpp(ω)e-γ1|ωα1/Uc|e-γ2|ωα2/Uc|e-jωα1/Uc
f0=U0/(3.68δ),δ=0.37L(U0L/ν)-0.2
(14)
式中,φpp(ω)为脉动压力的自功率谱密度,γ1、γ2为周向和轴向的衰减因子;α1、α2为X、X′两点周向和轴向的距离;Uc为外部流体的对流速度;L为所考虑位置至回转体顶端距离。对于未分离的湍流边界层,这些参数的取值如下:
Uc=0.65U0,γ1=0.32,γ2=0.7
文献[8]中推导了圆柱壳的传递导纳函数:
MpXX′(ω)=M10(ω)(Π(Kr)+Π(Kr′))
(15)
式中,M10(ω)为柱壳的输入点导纳,文献[8]中也给出了计算公式;Π(Kr)为柱壳传播函数,Π(Kr′)为绕柱壳一周后到达被激励点的响应。它们为第二类零阶Hankel函数之差:

圆板和内部声场由于没有外部激励,因此:
P2=P3=P4=0
4 计算分析
根据前面建立的计算模型计算给定参数下的声呐腔自噪声。本文柱壳、圆板都选用不锈钢材料。相关几何参数以及外部流场参数见表1。

表1 计算参数
图3为用波动法、均值导纳法计算得到柱壳到圆板的直接耦合损耗因子的比较。均值导纳法比波动法的计算简便。柱壳到圆板的直接耦合损耗因子的波动法的计算值根据文献[9]中给出的公式进行计算。从图中可以看出,波动法、均值导纳法两者能给出基本一致的结果。这与文献[9]中的结论一致。图4为湍流边界层柱壳的输入功率的图谱。图5为声呐腔的自噪声声压级图谱。
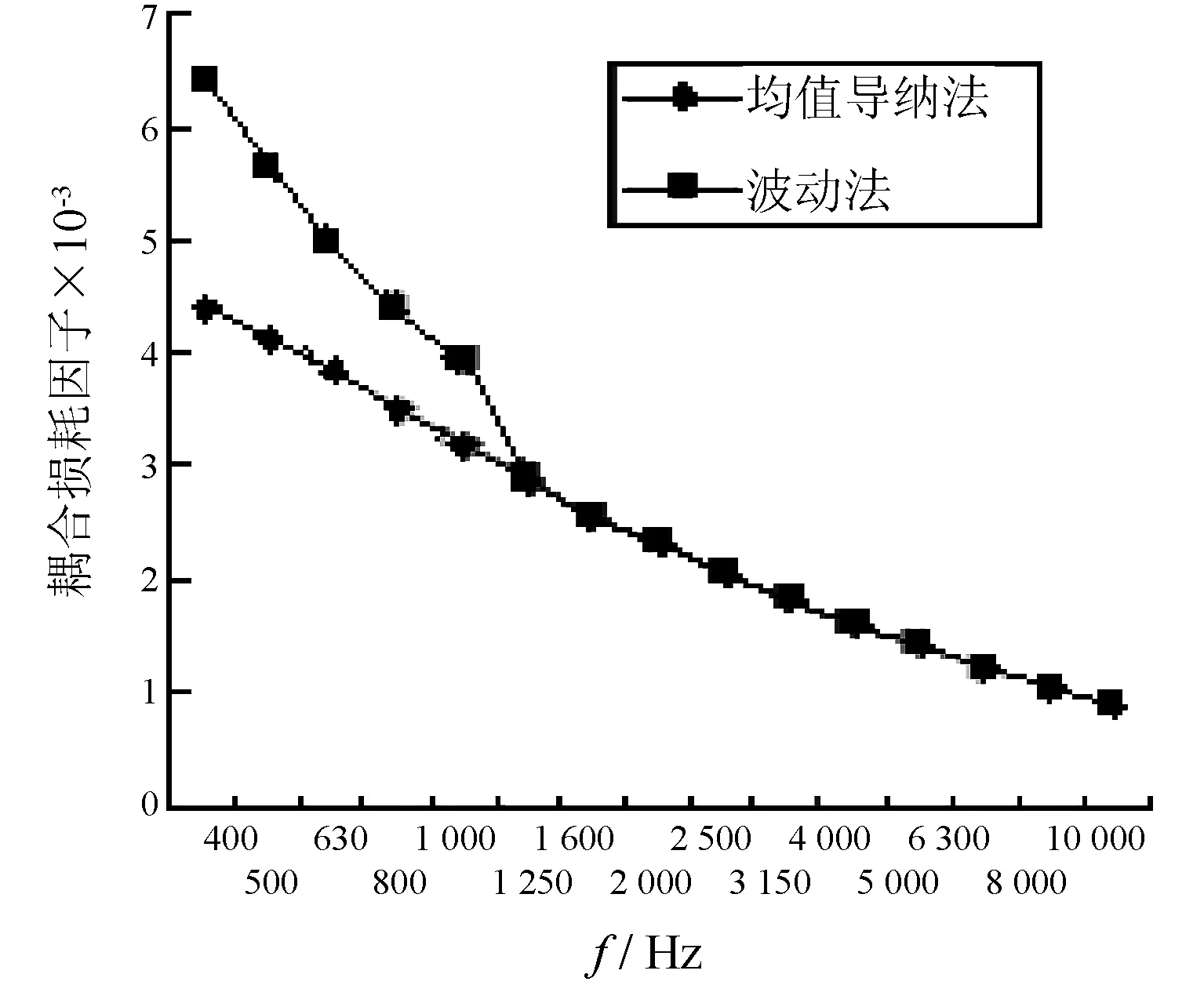
图3 模型一柱壳到圆板的CLF的比较
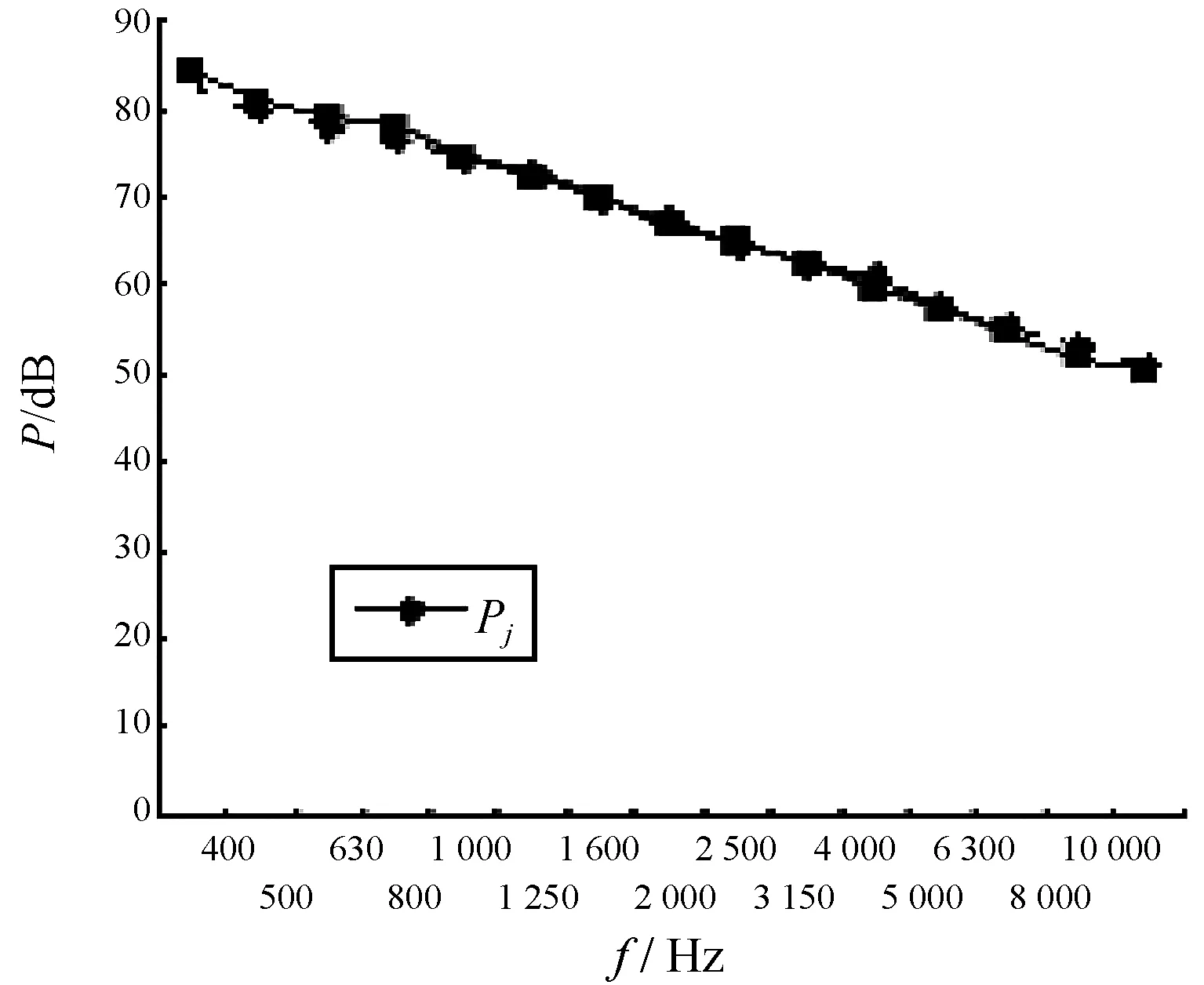
图4 湍流边界层对柱壳的输入功率级
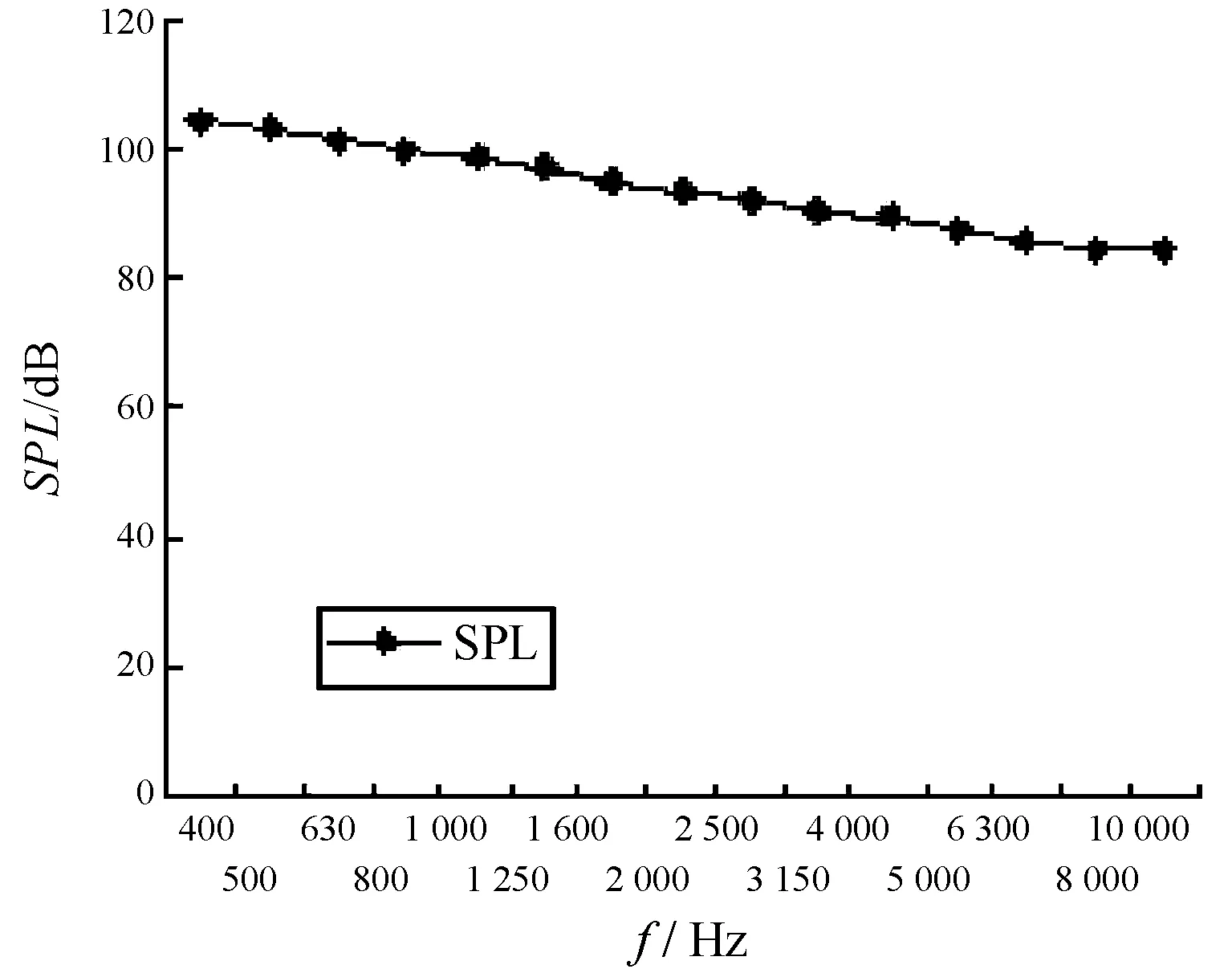
图5 声呐腔自噪声声压级
图3~图6中横坐标的频率为1/3倍频程中心频率,图4中纵坐标为功率级,基准值Po=10-12W,图5中声压级的基准值为10-6Pa。
为了更好地比较波动法与均值导纳法计算耦合损耗因子的结果,此处再给出一个算例。参数如下:半径R=1 m,L1=2 m,外部流场参数与上相同。柱壳到圆板的直接耦合损耗因子计算结果比较如图6。图6的结果比较更进一步地说明了波动法与均值导纳法在计算耦合损耗因子上的一致性。

图6 模型二柱壳到圆板的CLF的比较
5 结 语
本文着重介绍了利用均值导纳法计算耦合损耗因子,计算过程中利用到了经典统计能量分析参数,并与利用波动法得到的耦合损耗因子的值进行了比较,两者基本相同。另外,计算了复杂结构湍流边界层的输入功率,推导出了沿柱壳对称轴方向均匀来流对柱壳的输入功率的表达式。给出了一具体的算例,计算结果与有关文献结果相符。实际的声呐罩罩壁多为正交异性材料玻璃钢,对于正交异性材料壳的SEA参数的计算还在研究当中,也是以后统计能量分析研究的重点。
[1] 盛美萍,孙进才,王敏庆,等.直接和间接耦合损耗因子的计算方法[J].噪声与振动控制,1997(6):1-6.
[2] 盛美萍,王敏庆,孙进才.多点连接结构振动响应的均值导纳法预测[J].西北工业大学学报,1999,17(2):171-175.
[3] 张娟,李天匀,刘敬喜,等.空间不均匀湍流边界层激励下声呐腔自噪声统计能量分析[J].中国舰船研究,2007,2(6):24-29.
[4] 俞孟萨,叶剑平,等.船舶声呐部位自噪声的预报及其控制技术[J].船舶力学,2002,6(5):80-94.
[5] 俞孟萨,李东升.统计能量法计算声呐自噪声的水动力噪声分量[J].船舶力学,2004,8(1):99-105.
[6] 姚德源,王其政.统计能量分析原理及其应用[M].北京:北京理工大学出版社,1995.
[7] 钱斌,杨世兴,盛美萍,孙进才.封闭圆柱壳的振动响应特性研究[J].机械科学与技术,2002,21(1):122-126.
[8] 钱斌,汪源源,盛美萍,等.距离对板壳结构传递点导纳得影响[J].西北工业大学学报,2005,23(2):156-160.
[9] 杨晓华,姚德源.有限长圆筒壳与圆板连接的耦合损耗因子研究[J].战术导弹技术,2002,3(2):34-37.
