舰船概念设计多目标优化和多属性决策研究

1 引 言

在舰船概念设计中，设计者经常要完成的工作是生成多个船型方案，并从中筛选出1个或者多个综合性能较好的方案。这实际上是一个多目标优化和决策的问题。

多目标优化问题可以描述为：一个由满足一定约束条件的决策向量组成的向量，使得一个由多个目标函数组成的向量函数最优化。目标之间通常是相互冲突的。优化意味着要找到一个使所有目标函数都可接受的解。由于舰船本身技术性能的复杂性，采用传统的设计方法获得多目标优化的最佳船型概念是相当困难的。对于多目标优化问题，随着优化技术和计算机技术的发展，从20世纪80年代开始，进化算法开始应用于解决多目标问题。目前涌现出很多种多目标进化算法，已经形成了一个热门的研究领域[1]。

对于多目标优化问题，当Pareto最优解集求出来之后，还需要根据决策者的偏好，挑选出最后的折中解或最优解。这是一个综合评价问题，即对多属性体系结构描述的对象系统做出全局性、整体性的评价[2]。多属性决策方法作为运筹学的一个分支，具有对评价对象描述精确的优点，能够处理多决策者和多指标的对象。它通过化多为少和分层处理，直接给出排序。它是一种应用广泛的决策方法[3]。

本文将多目标进化优化技术与多属性决策方法结合起来，讨论了舰船设计中的优化和决策问题。对于多目标优化问题，采用改进的非支配解排序的多目标进化优化算法(NSGA II)[4]求出Pareto最优解，由这些Pareto最优解构成决策矩阵，使用基于信息熵和层次分析法组合赋权求得权值，然后用逼近理想解的排序方法(TOPSIS)[3]进行多属性决策(MADM)研究，对Pareto最优解给出了排序。文中讨论了1艘水面舰船概念设计的实例。

2 模型和求解

舰船概念设计需要考虑作战、技术、经济、安全等性能，这是一个多目标优化和决策的问题。在多目标优化的Pareto解集求出后，设计者还需要在多个优化方案中寻求一种综合性能最优的结果。以追求两个目标函数最大为例，图1显示了这种优化和决策的过程。

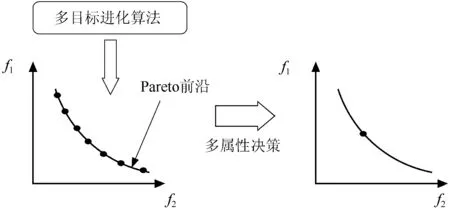
图1 Pareto最优解和决策过程示意图

2.1 多目标优化

一个多目标优化问题可以表述为如下形式：

minF(x)=[f1(x),f2(x), …,fn(x) ]

(1)

x=[x1,x2,…,xl]

s.t.hi(x)=0i=1,2,…,I

gj(x)≤0,j=1,2,…,J

式(1)表示了n个优化属性准则，l个决策变量，I个等式约束和J个不等式约束的多目标最小化优化问题。

在多目标优化中，由于目标之间相互冲突，很难找到一个真正意义上的最优解，而存在一系列解，其特点为至少存在一个目标优于其他所有的解，这样的解称之为非支配解，或Pareto解，这些解的集合即为Pareto最优解集。求解多目标优化问题的主要任务是求得该优化问题的Pareto最优解集。

在众多多目标优化算法中，多目标遗传算法的应用研究最为广泛。遗传算法通过对一个种群进行运算操作，在一个进化代中可以得到多个Pareto最优解，因此，它是求解Pareto最优解集的一种有效算法。NSGA II算法最早由印度研究人员SRINIVAS和DEB提出[5]，他们将非支配排序思想引入遗传算法，把多个目标函数的计算转化为虚拟适应度的计算，用于求解多目标优化问题。NSGA的基本原理是基于对个体的几层分级实现种群的非支配排序，在选择操作执行前，群体根据支配与非支配关系排序，所有非支配个体被排成一类，这些个体共享虚拟适应度值，依此逐步对剩余的个体进行分级并赋予相应的虚拟适应度。NSGA II是以NSGA为基础进行改进的非支配排序遗传算法，采用快速非支配排序过程、精英保留策略和无参数小生境操作算子，克服了传统NSGA的计算复杂度高、非精英保存策略和需特别指定共享半径的缺点。

2.2 多属性决策

实际上，多目标问题的求解还是一个决策问题，而不仅仅是一个优化问题。当Pareto最优解集求出来之后，还需要根据决策者的偏好，挑选出最后的折中解或最优解。决策是基于方案的，决策者更希望通过对多个方案进行权衡后做出选择。

HWANG和YOON[6]开发的逼近理想方案的序数偏好方法(TOPSIS)建立在所选择的方案应与理想方案的差距最小，并且和负理想方案差距最大的理论上。可以将关于m个方案n个属性的多属性决策问题看成在n维空间中m个点构成的几何系统中进行处理。此时，所有的方案可以作为该系统的解。TOPSIS通过和理想解的相近程度，同时考虑到理想解和负理想解的距离来判断方案的优劣。这种方法简单，可以产生清楚的解的偏好顺序。

TOPSIS方法使用属性的偏好信息，即需要属性的权重集。它的解依赖决策者的赋权方法。在多属性决策中，有很多的赋权方法，大致可以分成主观赋权、客观赋权和组合赋权3种[7]。主观赋权方法是决策者给出偏好信息的方法，主要有特征向量法、最小平方和法和层次分析法等；客观赋权方法是基于决策矩阵信息的方法，如主成分分析法、信息熵法和多目标优化方法等；组合赋权是主观和客观赋权相结合的一种赋权方法。本文将层次分析法和信息熵法组合起来，以期得到更加合理的综合权重，然后再用TOPSIS方法得到最后的Pareto最优解排序。

3 算例和讨论

采用上述过程，讨论了1艘水面舰船概念设计的实例[8]，该舰船的数学模型采用美国麻省理工学院水面船设计综合模型[9]。优化模型简述如下。

3.1 已知参数

持续速度30 kn，续航速度20 kn，续航距离6 400 km，自持力45 d，士兵58人，有效负载247.65 t。

3.2 优化设计变量

该优化问题共有45个变量，其中16个离散变量。基本设计变量8个，即水线面长度LWL，船宽B，甲板层数Ndecks，菱形系数CP，最大横剖面系数CX，船体平均甲板高度HDKh，舱底高度BILGE和舱室甲板高度HDKd。

推进系统参数包括推进器数量、效率、润滑油重量、螺旋桨数量、桨直径、推进轴长度。船舶控制系统参数为导航系统重量、稳定翼数量；作战系统的参数为阻力系数、声呐面积、重量、重心高度等。

3.3 约束条件和目标函数

1) 变量约束条件：

LWL/B=7.5～10

B/T=2.8～3.7

(2)

性态约束条件

排水量/LWL=45～65

GM/B=0.09～0.122

(3)

2) 目标函数一共取6个：

(4)

前5个目标函数为相对偏差。其中，kWG为发电机功率；kWGREQ为要求功率；PI为安装的轴马力，PIREQ为达到持续速度所需要的轴马力；VTR为需要容积；VTA为实际具有的容积；ATR为需要面积；ATA为实际面积；DELTAFL为全排水量；WT为总重量。

从舰船设计的角度看，前5个指标必须都大于零。因此，它们也是约束条件的一部分。电机功率、轴马力的误差以及建造费用越小越好，容积、面积和重量偏差越大越好。表1给出了NSGA II方法的参数设定情况，一共得到875个最优解。

表1 NSGA II方法参数设定

图2～图6给出了6个目标之间的Pareto最优解的散点图，横坐标均取为重量相对偏差。图中用实线给出了Pareto前沿。

针对这6个属性，根据层次分析法[10]给出判断矩阵P：

(5)

图2 重量偏差和功率偏差间的散点图

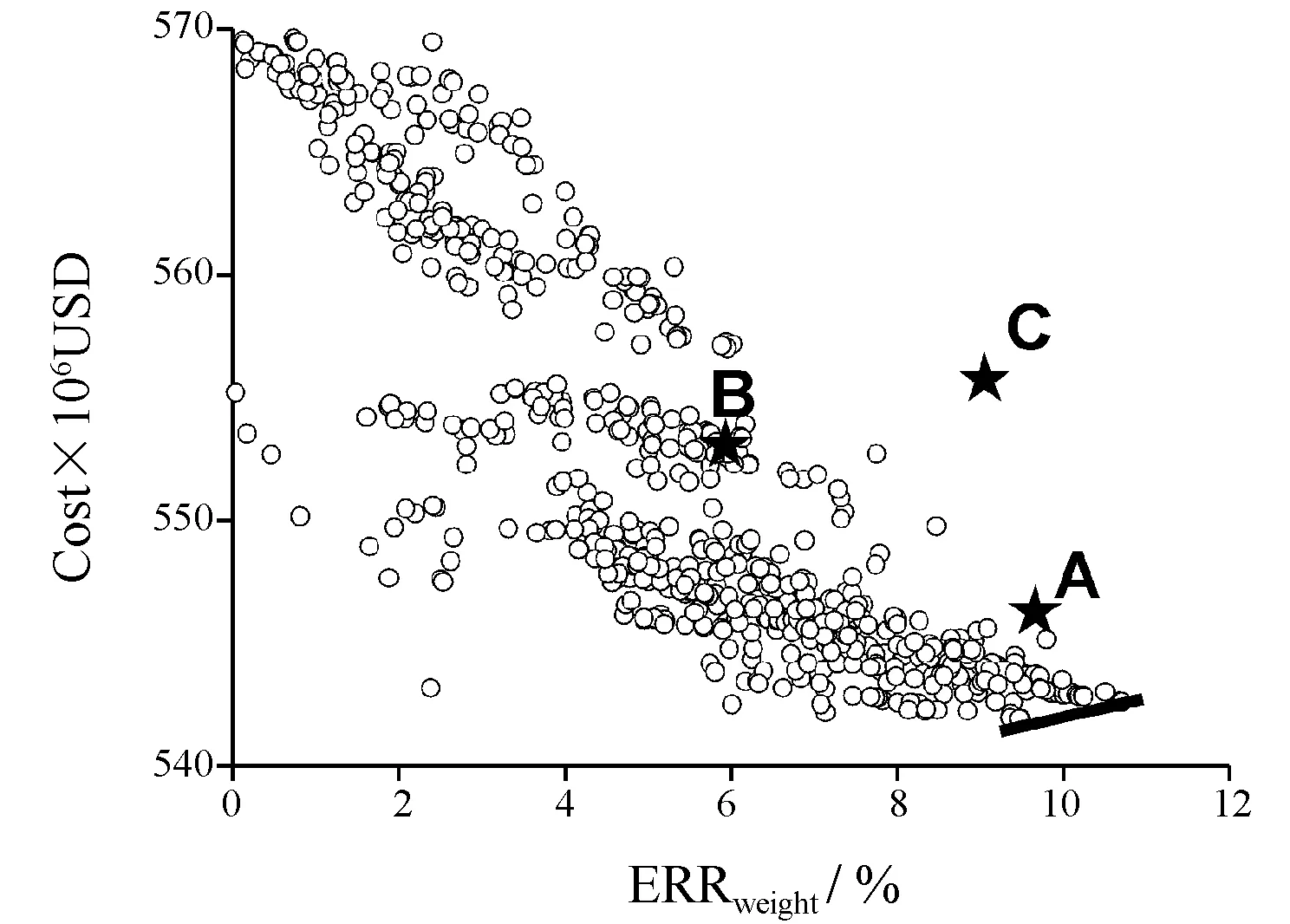
图3 重量偏差和费用间的散点图

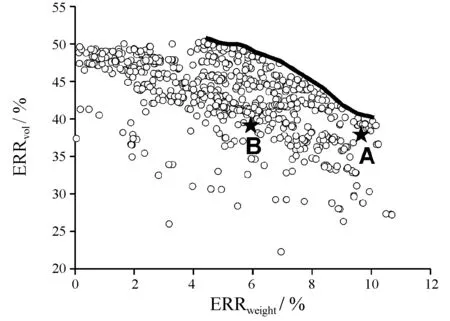
图4 重量偏差和容积偏差间的散点图

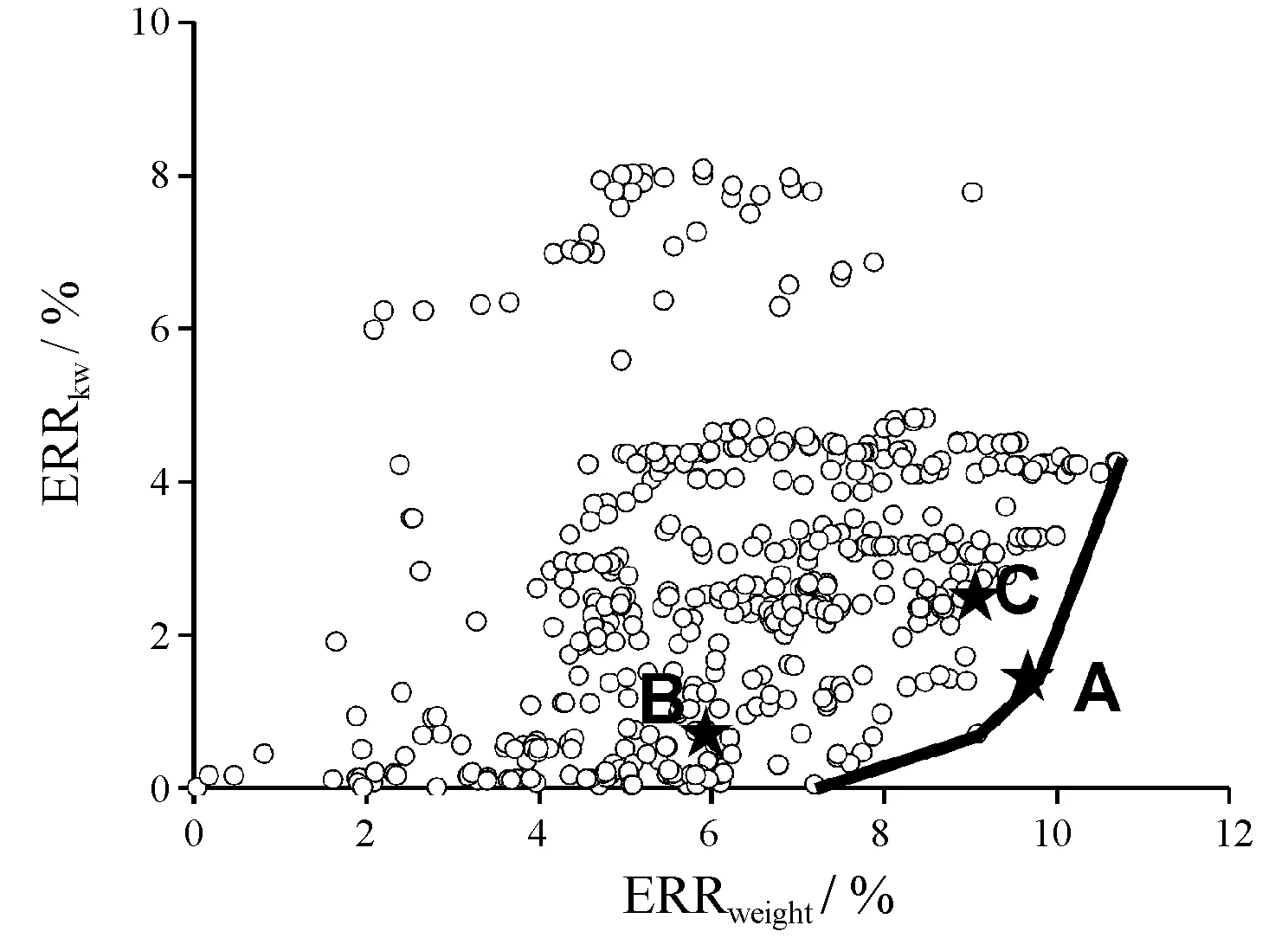
图5 重量偏差和功率偏差间的散点图

图6 重量偏差和面积偏差间的散点图

求得P矩阵的最大特征值为λmax=6.467 3，一致性指标C.I.和一致性比例C.R.分别为：

(6)

当C.R.<0.1时，即要求决策者判断的一致性与随机生成判断的一致性之比小于10%，认为判断矩阵的一致性是可以接受的。求解用λmax构成的关于属性权重的线性方程组，得到权重集(即主观偏好信息)：

λ={0.325 0,0.156 4,0.173 8,0.135 4,

0.117 4,0.092 0}

(7)

根据信息熵法，得到的权重集(客观赋权)为:

w={0.689 3,0.160 9,0.007 6,0.007 1,

0.135 0,0.000 1}

(8)

利用偏好信息λ对客观赋权w进行修正：

(9)

得到比较准确的权重：

w0={0.838 0,0.094 13,0.004 941,0.003 596,

0.059 28,3.441 4×10-5}

(10)

可见，建造费用的权重非常小，它对决策的影响最小。

为了在875个Pareto最优解中挑选最终解，先构成875×6的决策矩阵D(即6个目标函数构成决策矩阵的列)，再运用TOPSIS方法计算综合排序指数，以此指数的从大到小排列，得到最优解从优到劣的排序。

表2给出了是否计及偏好时，排序第1的方案结果。

表3 考虑偏好与否后排序结果及比较

这3个方案分别标识为A，B，C，它们用★号表示在图2～图6中。从图5中可以得知，基于客观赋权和TOPSIS方法得到的结果(方案A)位于Pareto前沿中部位置。考虑了决策者的偏好信息后的方案B，前5个指标都是优于方案A的，但是费用稍高一些。从决策的角度来看，通过费用的少许增加(1.24%)，能够换来其他指标的提升，特别是前两个指标提升更加明显。这种选择是可行的。依据AHP的偏好信息进行修正后，决策结果更加合理一些。

从多目标优化的角度来看，文献[8]给出的方案A和B是一个劣解(在图4和图6中，因C方案的函数值太小，未表示出来)。

4 结束语

本文采用多目标进化优化算法求出Pareto最优解，使用组合赋权及TOPSIS方法对Pareto最优解给出了排序。数值算例表明，多目标进化优化算法得到的最优解分布比较均匀，采用组合赋权方法能够将客观赋权和决策者的经验结合起来。将多目标优化方法和多属性决策方法综合运用，能够迅速获得船舶的最优概念设计方案，结果合理。这种综合方法，也可用于其他舰船的设计中。

[1] 崔逊学.多目标进化算法及其应用 [M].北京：国防工业出版社, 2006.

[2] 陈衍泰,陈国宏，李美娟.综合评价方法分类及研究进展 [J].管理科学学报, 2004, (2):69-79.

[3] 徐玖平,吴巍.多属性决策的理论与方法 [M].北京：清华大学出版社, 2006.

[4] DEB K, PRATAP A,ARGRAWAL S,MEYARIVAN T. A fast and elitist multi-objective genetic algorithm: NSGA II [J]. IEEE Trans. Evolutionary Computation, 2002, 6(2):182-197.

[5] SRINIVAS N,DEB K. Multiobjective optimization using non-dominated sorting in genetic algorithms[J]. Evolutionary Computation, 1995, 2:221-248.

[6] HWANG C L ,YOON K. Multiple attribute decision making- methods and applications: a state-of-art survey [M]. New York: Springer-Verlag, 1981.

[7] 江文奇.多属性决策的组合赋权优化方法 [J].运筹与管理, 2006, 15(6):40-43.

[8] ANIL K A. Multi-criteria analysis in naval ship design [D]. MS Thesis, Naval Postgraduate School, Monterey, California, 2005.

[9] SHAHAK S. Naval ship concept design: an evolutionary approach [D]. MS Thesis, MIT, 1998.

[10] SATTY T L. The Analytic Hierarchy Process[M]. New York:McGraw-Hill, 1980.