水下翼型水动力学与声学研究进展
2008-04-24董仁义,吴崇健
1 引 言
翼型在工程中应用广泛,最初关于翼型的研究集中在航空领域,针对翼展为无限长的等剖面直升机翼的空气动力特性做了大量研究。翼型是研究翼面空气动力特性的基础,飞机机翼、尾翼,导弹翼面,直升机旋翼叶片和螺旋桨叶片都是常见的翼面。翼型也是各种水下螺旋桨设计的基础,国内多采用50年代以前美国NACA(后称NASA)为飞机设计研制的NACA6或NACA16系列翼型[1],通常也能满足船舶工业的要求,后来也采用了国外根据50年代翼型设计及利用边界层计算新发展而设计出的水下新翼型[2]。
2 板壳体的力学特性
目前板壳和板壳体的力学特性研究已经发展得很成熟了。尽管空气中结构声辐射和声传输的主动控制研究在国内外已经取得了一系列的进展[3-15],但对水下结构声辐射和声传输的主动控制研究尚属少见。由于空气中结构声辐射和声传输的主动控制研究主要是以飞机和汽车为研究背景,未涉及水的加载效应对结构振动声辐射的影响,也没有考虑空气和水两种流体介质间特性声阻抗失配对结构声传输的影响。水的加载效应会改变结构的固有频率和阻尼,进而对结构的振动和声辐射产生影响[16,17]。
2.1 板壳的力学分析方法
水下翼型一般由板壳组成。目前板壳结构的二维计算模型主要基于以下理论:经典层合板理论(Classical Laminated Plate Theory)、一阶剪切变形理论(First-order Shear Deformation Theory)、高阶剪切变形理论(High-order Shear Deformation Theory)和分层理论(Layer-wise theory or Discrete-layer theory)[18]。其中一阶剪切变形理论通常又称为Mindlin板弯曲理论(Mindlin plate theory)。
基于一阶剪切变形理论的Mindlin板(壳)单元由于对横向剪切效应较显著的中厚板以及复合材料板壳的总体行为的计算是可以满足工程精度的,且只需C0连续性,推导方便且易于程序实现,在工程分析中受到了广泛的重视。此理论认为:原来垂直于板中面的直线在变形后仍保持为直线,但因为横向剪切变形的结果,不一定垂直于变形后的中面。基于此理论的板单元中,挠度w和法线转动θx及θy为各自独立的场函数。而w和θx及θy之间应满足的约束条件,根据变分原理的方法引入能量泛函。通常认为Mindlin板单元适用于中厚板壳的计算[19-22]。但在应用Mindlin板(壳)单元计算薄板(壳)时,很容易产生剪切闭锁。产生这一问题的根源在于对挠度和转动采用了同阶的插值表达式,使得剪切应变的约束条件未能精确满足,在板壳很薄时导致不确定地夸张了剪切应变能项的量级而造成的。避免剪切闭锁的方法目前主要有以下3种[23]:减缩积分方法、假设剪切应变方法和替代插值函数方法。此外,当用板单元分析壳体时,如某点处各单元共面(或近似共面),会使结构刚度出现奇异性。另外,在面内引入了垂直单元平面的旋转自由度,研究带旋转自由度的平面元的起因就是为了避免使用板单元在拟合壳体时结构扁平处极易出现的方程病态[24]。文献[25]推导了基于Mindlin板弯曲理论的四结点等参板壳单元,为避免剪切闭锁,利用域内一致和边界一致概念,以最小二乘法求出对剪应变的单独插值函数。
2.2 水下壳体结构—流体耦合的声学特性
船舶水下的许多结构,如舵叶壳体、耐压壳体都可以用板壳结构来模拟。对结构的振动声辐射计算可分为两类:结构—流体耦合计算和无耦合计算。 耦合计算适用于结构—流体耦合问题,如结构在水中的振动声辐射问题,即必须考虑流体加载对结构响应的影响。在耦合计算中,结构和声场响应是同时求解的。无耦合计算中适用于不需考虑流体加载对结构响应影响的问题,如结构在无限域空气中的振动声辐射问题,计算时可先求出结构响应,再从结构响应求出声场响应。
对结构声学的数值分析方法可以分为两大类:离散方法和能量方法。能量方法主要是指统计能量分析(SEA)和能量有限元法(EFEA)。能量方法适用于中高频激励作用下模态密集结构振动与声的计算分析。离散方法主要是指有限元法FEM和边界元法BEM。离散方法适用于中低频激励作用下的复杂结构振动与声的计算分析。目前数值方法在结构—流体耦合计算中得到了广泛的应用,对结构一般都采用有限元法进行离散,对流体介质的处理可采用有限元法、边界元法和无限元法等。其中,边界元法在处理外部自由声场时是最常用的数值方法。另外,双渐进法(DAA)在结构—声学流体耦合计算中也备受重视,它主要被广泛应用于求解结构在瞬态激励作用下的结构—流体耦合问题[26,27]。
对加筋板的声辐射研究,早期主要是以无限大具有相同加强筋的薄板为研究对象[28,29]。近来,吴文伟[30]也对集中力作用下的无限大具有相同加强筋系平板,采用傅立叶变换技术在波数域求得了辐射声压的解析表达式,并计算分析了平板厚度、加强筋间距和肋骨惯性矩对辐射声压的影响。对实际的有限尺寸的加筋板,张升明等[31]采用有限元和边界元法,以距离中心1 m处的声压级为标准,在相同模态条件下计算分析了无限障板中加筋板的结构参数与加筋板振动噪声的关系,他们的研究结论对分析实际结构的振动声辐射及其控制具有一定意义。
对加筋板的声辐射计算,可采用以结构表面声压和速度为边界量的直接边界元方法,这种边界元方法只适用于具有封闭表面的结构,离散结构表面的边界单元只能有一面与流体介质相接触。这样对加筋板进行振动声辐射计算时,需要对其包含加强筋在内的整个封闭的表面进行离散,也就是沿厚度方向有两层边界单元,其计算工作量是非常大的,也是不经济和不必要的。以结构表面的声压差μ和速度差σ为边界量的间接边界元方法可用于非封闭结构的声辐射计算,其边界积分方程的形式为[32]:
(1)
式中:p为声压;n为结构表面S的内法向单位矢量;Q为S上任意点;P为空间中任意点;G(Q,P)为自由场格林函数。采用间接边界元法计算加筋板的声辐射时,沿厚度方向就只需划分一层边界单元,但为考虑加强筋的声源效应和声障效应,仍需对加强筋也采用二维单元进行离散,计算花费也较大。所以目前对加筋板的声辐射计算基本上都是基于Rayleigh积分进行的[33,34],也就是在计算加筋板的声辐射时实际上是按无限障板中板的声辐射来计算的,仅考虑了加强筋对板的振动响应的影响,即只考虑加强筋的振动效应。另外,在计算时,如不需要考虑流体的加载效应,可在求出结构响应后,直接应用远场Rayleigh积分求出声场响应。如需考虑流体的加载效应,就得采用表面Rayleigh积分,再结合结构的动力方程联合求解[35,36]。
应用成熟的商业软件是进行水下结构(甚至全船模型)振动和声学计算的途径之一。目前已出现了不少较为成熟的商业有限元及边界元软件,如ANSYS, MSC/NASTRAN, SYSNOISE等。其中,SYSNOISE软件既含有有限元技术,又含有边界元技术,可计算一般复杂弹性结构的水下耦合振动问题。其优点是对声场的后置处理功能很强,可计算结构的辐射声功率、激励力的辐射声功率效率、矢量声场、声场的质点振速分布、远场指向性等。但该软件的有限元+边界元的耦合技术并不十分成熟[37]。ANSYS, MSC/NASTRAN软件只含有限元技术,其声场后处理功能较弱,并且需要在流体域划分有限元,结点多,计算量大。文献[38-43]将ANSYS和SYSNOISE结合,用ANSYS计算结构振动响应,而后提取结构表面位移,输入到SYSNOISE计算声场。文献[44-46]将MSC/NASTRAN软件和SYSNOISE软件结合,用MSC/NASTRAN计算结构流固耦合振动响应,而后提取结构表面位移信息,输入边界元程序SYSNOISE计算声场物理量。
曾革委[47]运用有限元+边界元法对潜艇舱段结构水下声辐射进行了数值分析。其基本思路是:1)利用ANSYS计算潜艇水下声辐射;ANSYS具有三维声学单元FLUID129以及FLUID130;由于ANSYS没有声学边界元,舷间流体及舷外流体都采用FLUID129有限单元模拟,对外部流场只能采取截断处理,用一个包围结构外部的有限球体(人工边界)模拟外部流场,在球体外表面附加FLUID130单元,模拟球面波扩散条件;流场球体大小取决于计算的最低频率;2)利用ANSYS+SYSNOISE计算潜艇舱段及尾部结构水下声辐射;先利用ANSYS进行潜艇结构空气中的模态分析,将结构有限元网格以及模态分析结果读入到SYSNOISE中,采用直接边界元(单壳体舱段结构)或间接边界元(尾部结构)耦合方法,计算远场辐射噪声以及壳体表面振动响应。
邹元杰[48]将流体分别视为不可压缩和可压缩两种情况建立了流固耦合方程,探讨了按可压缩流体计算水下结构振动响应对声辐射的影响。结果表明:流体可压缩性与流体边界条件、结构刚度和结构阻尼有关;在计算水下结构声辐射时,结构振动响应应当按可压缩流体计算。
应当注意的是:虽然将两个商业有限元软件结合方便了前处理和后处理,但目前对水下复杂结构流固耦合振动响应的计算主要是用商业有限元软件独立完成的,这就需要对无限大外部流体域也进行有限单元离散,使得计算量大大增加,并且用有限域代替无限域可能引入数值计算误差,也就是说目前应用商业软件在计算流固耦合振动响应时并未发挥边界元法的优势。
由于水中三维复杂结构的流固耦合计算较为复杂,为了降低计算量,工程上在考虑流体(水介质)对结构的作用时常常仅计及流体附加质量(不可压缩流体),而忽略流体阻尼[44-53]。文献[44-46]将MSC/NASTRAN和SYSNOISE结合,预报舰艇的振动声辐射特性,在计算结构响应时对流体的作用仅考虑了附加水质量的影响。这一工程处理的实质是忽略流体可压缩性对流体附加质量的影响,同时,忽略流体阻尼或结构声辐射阻尼[54]。文献[54,55]应用Rayleigh积分计算了无限大刚性障板中的板和加筋板的振动响应,探讨了流体可压缩性对结构振动固有频率及振动响应的影响,指出嵌于无限障板中的板结构振动响应的计算必须考虑流体可压缩性的影响。该文的研究很有意义,但水下结构的环境更多的是具有自由液面的半无限域(如水面舰船)或者无限域(如潜艇),而非Rayleigh积分所描述的具有刚性壁面的半无限域。文献[56,57]探讨了流体可压缩性对无限流体域中的三维复杂形状弹性结构的振动固有特性和振动响应的影响,以及按可压缩/不可压缩流体计算流固耦合振动响应对声辐射计算的影响,并对Rayleigh积分的影响作了讨论。
3 水下各种不同翼型的水动力研究
文献[58]建立了在船舶螺旋桨后部的舵模型,进行了流体结构直接耦合研究,它给出了三维水下结构的流固耦合模型,可模拟势流和粘性不可压缩流体,舵叶结构由壳单元进行有限元建模(图1)。结构和流体部分用虚表面来传递信息(图2),结果和结构实际变形一样,与非耦合的水动力模型实验具有很强的相关性(图3)。

图1 舵叶结构模型—剖视图
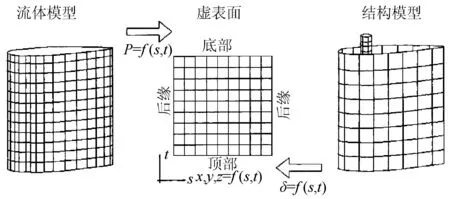
图2 流固耦合通过虚表面来实现

图3 舵和螺旋桨模型的风洞布置
文献[59]建立了三维尾流冲击模型,研究了在文献[58]情况下串列布置的水下振荡翼型(图4),利用建立的尾流冲击模型,根据改变系列参数,包括两翼型间的距离、振荡频率、跨距、俯仰角、垂直位置等,模拟得出布置在后部的翼型体由于尾流涡的冲击产生的压力波动。
国内也深入分析了水下舵叶的水动力。文献[60]对一种带副舵的潜艇尾升降舵建立受力模型(图5),综合分析水动力随主舵和副舵转舵角的变化规律,证明带副舵的潜艇尾升降舵能够提供比普通舵型更灵活和实用的操纵手段。
文献[61]比较了2种典型楔型舵翼型(图6)在不同航行状态下的空泡形态及其升/阻力系数的变化规律,表明随着来流攻角的增大,阻力系数呈现先减小后增大的趋势,且大空泡数条件下2种楔型舵的舵效相当,但有平行后体时的楔型舵在小空泡数条件下具有较高的舵效,需合理选择楔型舵以确保航行体具有稳定的航行性能。

图4 串列布置的水下翼型

图5 带副舵叶的潜艇尾升降舵

图6 楔型舵计算模型
文献[62]设计了一种新型的潜艇首舵——贝壳舵(图7),进行了系统的模型试验、水动力特性分析和操纵性计算,表明贝壳舵能在保持原型艇操纵性的基础上,简化潜艇首舵操舵机构,提高设备的可靠性。
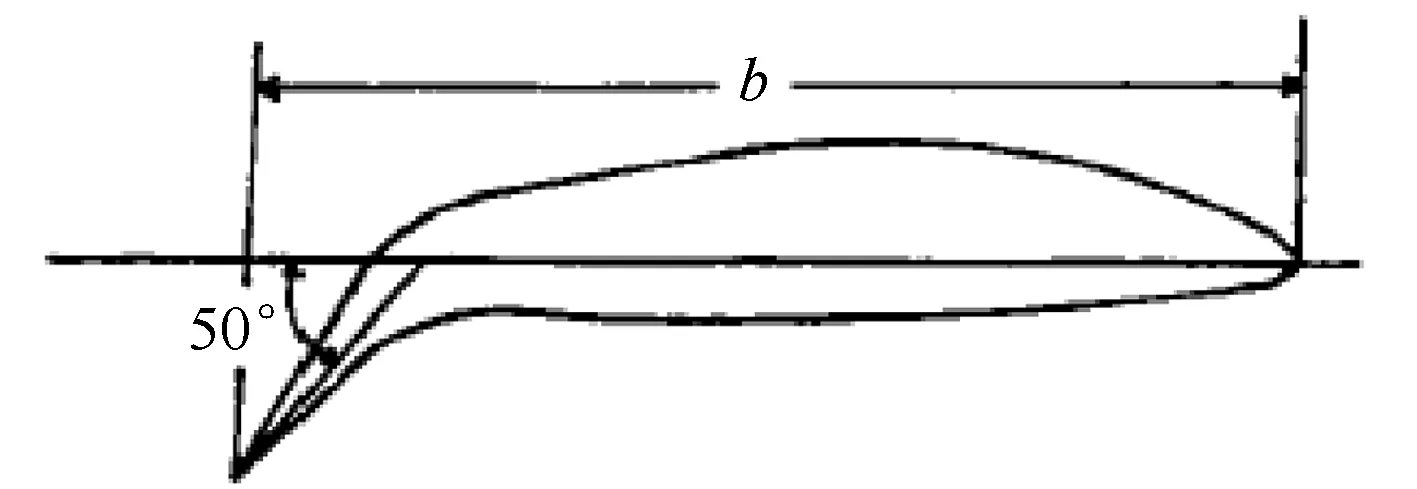
图7 贝壳舵翼型剖面(b为翼型弦长)
文献[63]采用RANS方程为基本方程,应用2层k-ε湍流模型封闭RANS方程,采用有限体积法离散方程,对小展弦比舵翼的三维绕流场进行了数值模拟计算。不同于通常的网格划分,采用了贴体坐标与空度法相结合的方法对舵翼的几何形状及其对流场的影响进行描述,计算结果与实验结果进行了比较,结果表明,可以对小展弦比舵翼三维流动的流体动力性能进行正确的预报,对其绕流场亦能给出合理的描述。
4 水下翼型的声辐射研究
目前,解决运动物体在运动介质中的声场辐射,最成功的方法是声学比拟方法。水下翼型在运动的流体介质中绕轴转动的声辐射问题也可以用声学比拟的方法来解决,国内有学者已经进行了一系列跟进的研究。
文献[64]采用N-S方程数值模拟了二维机翼的流固耦合运动,用弹簧系统代替实际固体变形产生的回复力和力矩。翼型的运动是两个自由度,即垂直于来流的振荡和转动振荡。为了模拟涡激振动,机翼的初始攻角取得比较大,以便产生周期性的旋涡脱落及周期性的流体动力,后者与弹簧系统相耦合,引起振动。
余志兴[65,66]研究了粘性流场中的水弹性计算,在此基础上,文献[67]推导有均流时二维运动物体的声辐射公式,研究了粘性流体通过二维翼型(图8)的声辐射。数值计算结果表明:在不同雷诺数时,声压随时间的变化不同,小雷诺数时,具有规则性,而大雷诺数时,具有非规则性,这是由于多个涡之间的相互作用而引起的;流体通过绕弹性中心的振动翼型引起的声辐射大于流体通过固定翼型的声辐射,单极子项对声场的贡献不容忽略。文献[68-70]对流体通过涡激振动机翼的声辐射进行了研究,首先考虑了机翼的强迫转动,只有一个自由度,进而考虑了更为复杂的机翼振动,有两个自由度,分别是上下振动和绕弹性中心的转动,得出流体绕涡激振动的机翼引起的声辐射大于流体绕固定机翼引起的声辐射,特别是当涡脱频率和机翼的固有振动频率一致时,声辐射达到最大,并且根据翼型的周期性涡发放,需要较大的攻角,而攻角的具体大小与翼型有关系,提出了可以利用改变翼型形状控制涡激噪声的可能性。

图8 机翼结构系统

图9 文献[71,72]的尾部模型
文献[71,72]针对带有舵翼的水下航行器尾部结构模型,研究舵翼(图9)对水下航行器尾部的振动及声辐射的影响,利用有限元和直接边界元法求解模型在流体中的动态特性。其计算步骤共分为4步:1)利用有限元方法对模型进行划分,并得到模型的“干”模态参数;2)根据上一步得到的结果,利用有限元和直接边界元的混合方法得到模型浸没在流体中的“湿”模态参数(图10);3)将得到的“湿”模态参数进行模态叠加获得模型在内部激励下的响应;4)根据模型表面的位移和速度得到周围流场的声压分布。结果显示舵翼结构与周围流体的相互作用很大,改变其尺寸和刚度会使得模型的声压发生很大的变化,同时流固耦合现象的存在使得模型在水中的频率明显下降,并且模态阶数的顺序也发生了改变。

图10 尾部“干”和“湿”频率
5 水下翼型实验研究
文献[73] 在小型循环水槽中进行两维翼(图11)水致振荡显示实验。流场显示以PIV技术为主,辅以染料示踪技术。试验证明了PIV技术可以应用于被动振动非定常复杂流场的测量中,并对两维翼流体旋涡诱发振动响应进行了分析。
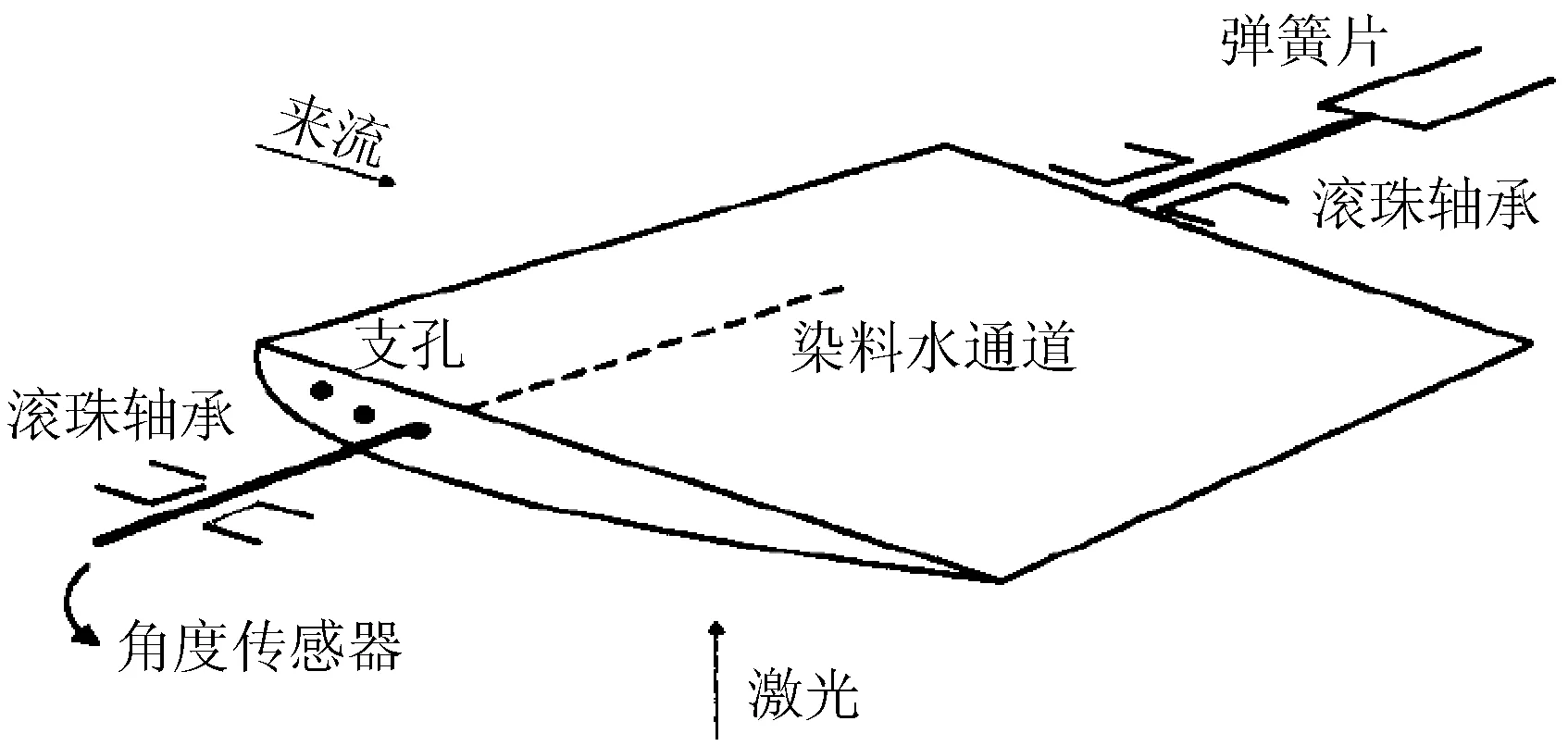
图11 模型安装示意图
文献[74]在重力式水洞中进行了水翼(图12)及半翼(图13)湍流边界层流场与噪声的实验研究。测量了水翼及半翼边界层附近的湍流脉动速度场;测量了半翼翼型表面3点处的压力脉动及其辐射噪声。测量了水翼内部测点的噪声及外部辐射噪声,在不同流速、不同攻角、光滑和粗糙翼面的情况下都进行了测量分析。试验结果发现,上述因素对模型的边界层湍流速度场有显著影响,15°攻角时,翼面附近湍流强度要比0°时大得多,粗糙翼面附近的湍流强度比光滑的大,而湍流强度随来流速度的变化不大,u(来流)方向和v方向的湍流强度量级相当;一般地,翼面压力脉动、翼内部噪声及外部噪声都是随来流速度的增大而增大,随攻角的增大而增大,粗糙翼面时的结果要比光滑翼面的大。从压力脉动与噪声测量结果和相应的流场测量结果比较可知,可以从湍流区域的湍流强度判断出声源强度的定性变化。

图12 水洞试验段与水翼模型

图13 水洞试验段与半翼模型
文献[75]总结了Anderson(1996)博士论文中对振动翼问题的实验,下面概括了水洞中的翼型俯仰试验。
Oshima在水洞中研究了沉浮和俯仰的NACA0012翼型,雷诺数分别从400到1 200和1 600,通过流场显示和涡测量实验跟离散涡方法数值模拟相互比较,研究了一系列频率和大幅度0(c)的运动。
Carr对NACA0012翼型进行了系统的动态失速研究,雷诺数是2.5e6。模型绕1/4长处,平均攻角为15°,作俯仰幅度为10°的正弦振动。他们对速度和压力进行了测量,对失速涡的生成和脱落进行了研究。失速时,随着俯仰力矩减少,升力大幅度增加。当失速涡离开振动翼,升力突然失去并且俯仰力矩出现一个负的峰值。以攻角为自变量,升力、阻力和力矩出现一个很明显的滞后现象。在动态失速中先后出现:1)升力突然升高;2)负力矩增长;3)最大阻力;4)最大前缘吸吮现象;5)吸吮波出现;6)出现力矩负值浮动;7)最大升力;8)最大负力矩。
Gendrich对加速度效应在动态时速涡形成的作用进行了数值模拟。他们得出前缘涡分离过程不是依赖于俯仰加速度,而是依赖于俯仰速度和瞬间攻角。
Robinson研究了动态失速涡沿NACA0015翼型展向和端部的形成,其中翼型俯仰从0°~60°。他们观察到靠近端部涡之间的相互作用阻止了前沿涡的疏运和升力提升,这是前缘局部吸吮导致的结果。第二个前缘涡也被观察到,其依赖于俯仰速度。压力的测量显示其几乎不依赖于雷诺数。
Vishal数值研究了同样的问题,条件同上,NACA0015翼型俯仰从0°~60°。数值模拟显示在翼型的吸吮表面存在两种不同的涡形成过程:动态失速涡和剪切层涡(其形成在动态失速涡之后)。动态失速涡和剪切层涡相互作用并最终合成一个更大的涡结构。这个涡结构接着跟后缘涡作用。这些涡依赖于俯仰速度和旋转轴的位置。当俯仰轴固定、俯仰频率加大时,动态失速延迟直到更大的攻角,这与McAlister结果一致。
近期,文献[76]为了认识吊舱式推进器操舵工况的水动力特性,进行了拖式吊舱推进器模型试验研究。试验测量了拖式吊舱推进器在不同转舵方向角的推力、扭矩及转舵力矩,所获得的流体动力数据能有效地解析实船操纵方式,并能为转舵 机构及吊舱结构的设计提供参考。文献[77]以1 500 t海监船为例,针对不同的舵型舵面积等参数,对单桨单舵船舵设计与操纵性能试验进行了研究;同时,哈尔滨工程大学黄胜教授的研究小组[78-80]系统地进行了多桨多舵水动力干扰研究,螺旋桨与舵副推力鳍相互干扰水动力性能数值计算以及舰船双桨双舵推进系统的水动力研究均采用了CFD数值实验方法,对水下舵与桨的水动力干扰进行了理论实验研究。
6 结 论
本文比较全面地分析了组成水下翼型的板壳体的力学特性,以及水下壳体结构—流体耦合的声学特性,综述了水下壳体的数值研究方法;同时综述水下翼型,主要是船舶中不同翼型结构的水动力研究,着重讨论了流体通过二维振动翼型的声辐射研究,并且对水下翼型的水洞实验给出了主要的实验结果。大部分的研究只是在基于单一水下翼型作周期运动或静止状态下进行分析,实验也是在水洞中用缩放比例的翼型模型进行,这些结果只能作为初步的工程应用基础。为此可开展以下几方面的研究:
1) 开展复杂工况下翼型的水动力研究,以此为基础进行翼型的水动力噪声分析及预报;
2) 探寻翼型非周期非线性运动冲击流体时的声辐射研究方法;
3) 采用理论研究和模型试验相结合的方法,建立对一组或多个翼型同时运动时分析翼型水动力学及声学特性的方法。
[1] 上官云信,周瑞兴,解亚军,等.一种新型低噪声水下动力螺桨翼型的实验研究[J].流体力学实验与测量,1998,12(2):63-73.
[2] SHEN Y T,EPPLER K. Wing sections for hydrofoils part 2: nonsymmetrical profiles[J].Journal of Ship Research,1981,25(3):191-200.
[3] FULLER C R.Active control of sound transmission /radiation from elastic plates by vibrational inputs.Ⅰ analysis[J].J.Sound&Vib.,1990,136(1):1-15.
[4] FULLER C R,HANSEN C H,SNYDER S D.Active control of sound radiation from a vibrating rectangular panel by sound sources and vibration inputs:an experimental comparison[J].J.Sound&Vib.,1991,145(2):195-215.
[5] FULLER C R,ELLIOTT S J,NELSON P A.Active control of vibration[M].San Diego:Academic Press,1996.
[6] HHNSEN C H,SNYDER S D.Active control of noise and vibration[M].London:E&Fn Spon,1997.
[7] NELSON P A,ELLIOTT S J.Active control of sound[M].London:Academic Press,1992.
[8] CLARK R L,SAUNDERS W R,GIBBS G P.Adaptive structures:dynamics and control[M].New York:JohnWileysons,Inc.,1998.
[9] RO J,BAZ A.Control of sound radiation from a plate into acoustic cavity using active constrained layer damping.Samrt Mater[J].Struct.,1999,8(3):292-300.
[10] PAN J,HANSEN C H,BIES D A.Active control of noise transmission through a panel into a cavity,Ⅰ:analytical study[J].J.Acoust.Soc.Am.,1990,87(5):2098-2108.
[11] QIU X J,SHA J Z,YANG J.Mechanisms of active control of noise transmission through a panel into a cavity using a point force actuator on the panel[J].J.Sound&Vib.,1995,182(1):167-170.
[12] 陈克安,马远良,孙进才.弹性结构封闭空间有源消声[J].声学学报,1994,19(6):434-443.
[13] 谢建良,陈南,钟秉林,孙庆鸿.封闭空间中结构声辐射的有源力控制研究[J].振动工程学报,1999,12(1):15-20.
[14] 杨军,李晓东,田静.有源约束层在对结构声辐射控制中的应用:Ⅰ.理论分析[J].声学学报,2000,25(1):56-60.
[15] 杨军,李晓东,田静.有源约束层在对结构声辐射控制中的应用:Ⅱ.数值计算[J].声学学报,2000,25(2):161-165.
[16] 诺顿 M P.工程噪声和振动分析基础(第一版)[M].北京:航空工业出版社,1993.
[17] FAHY F. Sound and structural Vibration: radiation , transmission and response[M]. London:Academic Press,1985.
[18] SAMANTA B, RAY M C, BHATACHARYYZ R. Finite element model for active control of intelligent structures[J]. AIAA Journal, 1996, 34(9): 1885-1893.
[19] 顾元宪,曾庆纲.一种新的四边形层合板与夹层板单元[J].大连理工大学学报,1997, 37(4): 392-397.
[20] 郑罡,朱菊芬.四节点类连续膜板(壳)单元[J].上海力学,1997, 18: 277-283.
[21] 朱菊芬,郑罡.带旋转自由度C0类任意四边形板(壳)单元[J].计算力学学报,2000,17(3):287-292.
[22] PRATHAP G, SOMASHEKAR B R. Field and edge-consistency synthesis of a 4-noded quadrilateral plate bending element[J]. Int. J. Numer. Methods Eng., 1988, 26: 1693-1708.
[23] 王勖成,邵敏.有限单元法的基本原理和数值方法[M].北京:清华大学出版社,1997.
[24] 刘红,唐立民,吕和祥.带旋转自由度的拟协调平面元[J].计算结构力学及其应用,1990, 7(4): 23-31.
[25] 邹元杰.水中阻尼复合壳体结构声振特性的数值分析[D].博士论文,大连理工大学,2004.
[26] GEERS T L,ZHANG P.Doubly asymptotic approximations for submerged structures with internal fluid volumes:formulation[J].ASME Transactions,Journal of Applied Mechanics,1994,69:893-899.
[27] ERGIN A.The response behaviour of a submerged cylindrical shell using the doubly asymptotic approximation method (DAA)[J]. Comput. Struct., 1997, 62 (6):1025-1034.
[28] MACE B R.Periodically stiffened fluid-loaded plates,Ⅱ:response to line and point forces[J]. J.Sound&Vib.,1980,73:487-504.
[29] MEAD D J.Plates with regular stiffening in acoustic media:vibration and radiation[J]. J. Acoust .Soc .Am.,1990, 88:391-401.
[30] 吴文伟,冷文浩,沈顺根.具有等间距相同加强筋板的声辐射[J].中国造船,1999,40(3):72-81.
[31] 张升明,潘旭初.板架结构的振动噪声研究[J].噪声与振动控制,1995,5:9-13.
[32] MOYNE S L,TEBEC J L,KRAEMER J C.Source effect of ribs in sound radiation of stiffened plates:experimental and calculation investigation[J].ACUSTICA,2000,86:457-464.
[33] MAIDANIK G,DICKEY J.Acoustic behavior of ribbed Panels[J]. J.Sound&Vib.,1988,123:293-307.
[34] MACE B R.Sound radiation from fluid loaded orthogonally stiffened plates[J]. J.Sound&Vib., 1981, 79:439-452.
[35] 黎胜,赵德有.流体加载下加肋板结构的声辐射特性研究[J].应用声学,2000,19(6):28-32.
[36] SGARD F,ATALLA N,NICOLAS J.Coupled FEM-BEM approach for mean flow effects on Vibro-acoustic behavior of planar structures[J].AIAA Journal,1994,32(12):2351-2358.
[37] 商德江,何祚镛.加肋双层圆柱壳振动声辐射数值计算分析[J].声学学报,2001, 26(3): 193-201.
[38] 徐张明,汪玉,等.船舶结构的建模及水下振动和辐射噪声的FEM/BEM计算[J].船舶力学,2002, 6(4):89-95.
[39] 徐张明,沈荣瀛,等.利用FEM/IBEM计算流体介质中的壳体的结构声耦合问题[J].振动工程学报,2002, 15(3): 363-367.
[40] 徐张明,汪玉,等.双层壳体的船舶动力舱振动与声辐射的有限元结合边界元数值计算[J].中国造船,2002, 43(4): 39-44.
[41] 童宗鹏,王国治.舰艇结构水下振动和声辐射特性研究[J].华东船舶工业学院学报(自然科学版),2003, 17(2): 18-22.
[42] 彭旭,骆东平.船舶结构建模及水下振动和辐射噪声预报[J].噪声与振动控制,2003,6: 9-12.
[43] 邹春平,陈端石,华宏星.船舶水下辐射噪声特性研究[J].船舶力学,2004, 8(1): 113-120.
[44] 杨德庆,郑靖明,王德禹,等.基于SYSNOISE软件的船舶振动声学数值计算[J].中国造船,2002, 43(4):32-37.
[45] 杨德庆,王德禹,刘洪林,等.舰艇振动声学特性数值分析[J].上海交通大学学报,2002, 36(11):1537-1543.
[46] 杨德庆,王德禹,刘洪林,等.某型艇近场噪声和自噪声数值计算[J].声学学报,2003, 28(5): 421-424.
[47] 曾革委.潜艇结构水下声辐射及其控制研究[R]. 701所博士后工作报告, 2005.
[48] 邹元杰,赵德有.按可压缩流体计算结构响应对声辐射的影响[J].大连理工大学学报,2004(1):85-90.
[49] EVERSTINE G C.Prediction of low frequency vibrational frequencies of submerged structures[J]. J.Vib.Acoust., 1991,113:187-191.
[50] 吴绍亮,金咸定.流固耦合计算方法在船舶局部结构中的应用[J].振动与冲击,2003, 22(4): 26-28,31.
[51] 智勇,吴卫国,翁长检.高速船舱壁加筋板流固耦合振动分析[J].工程力学,2003, 20(2): 159-162.
[52] 夏利娟,吴卫国,翁长俭,金咸定.高速船垂向振动计算的流固耦合分析[J].上海交通大学学报,2000,34(12):1713-1716.
[53] 赵键.薄板和不可压缩流体耦合振动的边界元法研究[J].中山大学学报(自然科学版),1996, 35(1):7-11.
[54] 张升明.流体的可压缩性对弹性结构振动的影响[J].水动力学研究与进展,1994, Ser.A, 9(4):429-436.
[55] 张升明.流体的可压缩性对结构振动特性及响应的影响[J].舰船性能研究,1990(3):93-102.
[56] 邹元杰,赵德有.水下结构声固耦合振动的特征值计算[J].船舶力学,2004,8(2): 109-120.
[57] 邹元杰,赵德有.按可压缩流体计算结构响应对声辐射的影响[J].大连理工大学学报,2004, 44(1):85-90.
[58] TURNOCK S R,WRIGHT A M. Directly coupled fluid structural model of a ship rudder behind a propeller[J]. Marine Structures,2000,13:53-72.
[59] MOQIN H,BRAIN V,NEIL B.A three-dimensional wake impingement model and applications on tandem oscillating foils[J].Ocean Engineering, 2006,2:1-14.
[60] 余贤红,林俊兴.带副舵的潜艇尾舵受力分析[J].航海工程,2005,6:28-30.
[61] 蔡卫军,钱建平,尹韶平,等.2D楔型舵的空泡流场特性研究[J].鱼雷技术,2007,15(4):38-41.
[62] 牟军,许汉珍.潜艇贝壳舵的试验和理论研究[J].中国造船,1998,2:25-31.
[63] 杨俊,潘卫明.小展弦比舵翼三维绕流场的数值模拟计算[J].武汉交通科技大学学报,1999,23(2):119-122.
[64] 缪国平,刘应中,余志兴.二维机翼弹簧系统的涡激振动[J].船舶力学,2002,5:25-32.
[65] 余志兴,刘应中,缪国平.二维机翼弹簧系统的涡激振动[J].船舶力学,2002,6(5):25-32.
[66] 余志兴.粘性流场中的水弹性计算[D].上海:上海交通大学,1999.
[67] 刘晓宙,缪国平,余志新,等.流体通过二维振动翼型的声辐射研究[J].声学学报,2004,29(2):122-130.
[68] 刘晓宙,缪国平,余志兴,等.流体通过涡激振动机翼的声辐射研究[J].声学学报,2005,30(1):56-62.
[69] 刘晓宙,缪国平,唐春权,等.粘性流体通过二维振荡圆柱的声辐射研究[J].船舶力学,2002,6(4):75-88.
[70] 刘晓宙.旋涡运动与涡激噪声的研究[D].上海:上海交通大学,2000.
[71] TONG Z,ZHANG Y,ZHANG Z,etc.Dynamic behavior and sound transmission analysis of a fluid-structure coupled system using the direct-BEM/FEM[J].Journal of Sound and Vibration,2007,299:645-655.
[72] 张丹才,章艺,童宗鹏,等.舵翼结构对水下航行器尾部振动声辐射的影响[J].振动与冲击,2006,5:102-105,195.
[73] 吴有生,杜双兴,司马灿,等.两维翼水动力振动和流场显示的粒子图像测速实验[J].中国造船,2000,01:26-30.
[74] 罗柏华,刘宇陆.湍流边界层流场与噪声实验研究[J].试验力学,2001,16(4):378-386.
[75] 王肇.二维振动机翼的流场测量及数值分析[D].硕士论文,合肥:中国科学技术大学,2004,6.
[76] 谢清程,昌小冬,王根禄,等.吊舱式推进器操舵工况水动力试验研究[J].中国造船,2008,49:19-24.
[77] 周永兴,尤培培,陈海燕.单桨单舵设计与操纵性试验[J].中国舰船研究,2007,2(3):40-43.
[78] 覃新川.短翼水动力计算模型与多桨多舵水动力干扰研究[D].博士论文,哈尔滨:哈尔滨工程大学,2006,5.
[79] 郭春雨.螺旋桨与舵副推力鳍相互干扰水动力性能数值计算[D].博士论文,哈尔滨:哈尔滨工程大学,2006,11.
[80] 王诗洋.舰船双桨双舵推进系统的水动力研究[D].硕士论文,哈尔滨:哈尔滨工程大学,2007,2.
