主机隔振器刚度对船舶推进轴系冲击特性的影响
2008-04-24郭全丽,祝长生,邓轶
1 引 言
船舶推进轴系是船舶动力系统的重要组成部分,轴系的抗冲击性能是评估系统生命力的一个重要指标,船舶主机采用不同的隔振设计,会给轴系的冲击特性带来很大的影响。因此,分析主机隔振器刚度与轴系冲击特性的关系是十分必要的。
本项研究对轴系在冲击载荷作用下的冲击位移响应进行了建模及计算[1],对主机采用不同隔振形式后的轴系冲击响应特性进行了专门研究,研究结果可为轴系的抗冲击设计及主机的隔振设计提供参考。
2 模型的建立
本研究以某推进轴系为例,利用有限元法进行模型的建立[2],模型包括主机及其隔振器。
推进轴系由尾轴,中间轴,前、后支撑轴承,推力轴承,弹性联轴器,主机及螺旋桨等组成,建模说明如下:
1) 弹性联轴器
弹性联轴器的质量按照集中质量来考虑,其余部分按照无质量有刚度的轴段考虑。联轴器左右两端用一个弹簧相连接,弹簧系数的大小表示联轴器对转子位移的限制程度。在这个模型中,联轴器主动端与被动端的节点具有相同的节点坐标。

图1 弹性联轴器模型
2) 螺旋桨、推力轴承与轴段
螺旋桨按照集中质量来计算,螺旋桨轴与推进轴之间的连接按照刚性来处理。
推力轴承的模型只需考虑推力轴部分,其余部分不予考虑。
各轴段材料的弹性模量和密度分别为2.0E+11 N/m及7 800 kg/m3。
3) 主机及隔振器
建模时将主机简化为一个桶体,桶体的两端在轴承位置各有一个集中质量来模拟主机的端盖。电机的定子通过弹簧与基座相连,共用5个弹簧来模拟隔振器的弹性作用。
主机转子材料的弹性模量和密度分别为2.0E+11 N/m及7 800 kg/m3,转子上铁芯的比重为转子材料比重的72%。
简化后得到的推进轴系—联轴器—主机—隔振器系统的模型如图2所示。系统上各支撑轴承的位置同样在图2中标出。
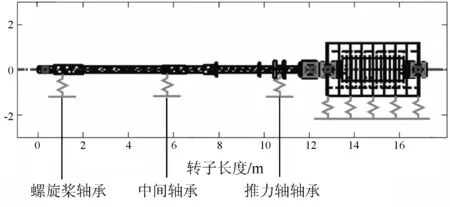
图2 推进轴系—联轴器—主机—隔振器系统模型
3 冲击响应计算的数学模型
本次计算采用半正弦加速度基础激励[3],表达式为:
(1)
由有限元模型得到推进轴系—主机—隔振器系统的冲击模型在基础激励条件下的运动微分方程为:
(2)


(3)
通过对上面的系统微分方程进行数值积分,就可以得到推进轴系—主机—隔振器系统在基础冲击作用下的瞬态位移响应,从而比较准确地估计基础冲击激励条件下轴系的性能。本次计算使用了龙格—库塔法进行计算。
计算的过程为先在给定的稳态转速下计算得到该转速条件下的稳态响应,然后再在原来的系统上增加由于基础冲击加速度所产生的冲击力,一直计算到新的稳态为止。
4 冲击特性计算
由于进行推进轴系—主机—隔振器系统的冲击特性计算的工作量很大,所以下面主要针对150 r/min稳定转速下的系统冲击特性进行分析计算。
计算用半正弦加速度激励的持续时间τ为0.1 s,脉冲幅值分别为50,100和200 m/s2。半正弦加速度激励的时间历程如图3所示。

图3 计算中采用的几种半正弦冲击加速度时间曲线
1) 稳定转速下基础冲击加速度的大小对系统冲击特性的影响
计算中,各支撑轴承刚度取为2.0E+8 N/m,弹性联轴器刚度取为8.4E+6 N/m,隔振器的刚度取为2.0E+6 N/m;螺旋桨处的阻尼系数为2.0E+4 N/m·s-1,轴承处的阻尼系数为2.0E+3 N/m·s-1,主机隔振器阻尼系数为5.0E+3 N/m·s-1。
基础半正弦冲击加速度分别为50,100和200 m/s2条件下(冲击方向为垂直方向),轴段上各支撑轴承(螺旋桨轴承、中间轴承和推力轴承)节点处冲击前(坐标原点处的点或圆)、后的运动轨迹如图 4~图6所示。

图4 冲击加速度为50 m/s2时各支撑轴承节点的冲击响应曲线

图5 冲击加速度为100 m/s2时各支撑轴承节点的冲击响应曲线

图6 冲击加速度为200 m/s2时各支撑轴承节点的冲击响应曲线
图7给出了不同冲击加速度条件下,轴系在垂直方向及水平方向上最大正向振幅和负向最大振幅随冲击加速度的变化曲线。

图7 轴系的最大正向振幅和负向最大振幅随冲击加速度的变化
2) 稳定转速下主机隔振器的刚度对阻尼转子系统冲击特性的影响
计算中,各轴承刚度取为2.0E+8 N/m,弹性联轴器刚度取为8.4E+6 N/m;螺旋桨处的阻尼系数为2.0E+4 N/m·s-1,轴承处的阻尼系数为2.0E+3 N/m·s-1,主机隔振器阻尼系数为5.0E+3 N/m·s-1;基础半正弦冲击加速度为100 m/s2。主机隔振器的刚度为2.0E+9 N/m、2.0E+8 N/m、2.0E+7 N/m和2.0E+6 N/m条件下,轴段上各支撑轴承(螺旋桨轴承、中间轴承和推力轴承)节点处冲击前(坐标原点处的点或圆)、后的运动轨迹如图8~图10和图11所示。
图12给出了在相同的冲击加速度条件下,轴系在垂直及水平方向上最大正向振幅和最大负向振幅随隔振器刚度的变化曲线。

图8 隔振器刚度为2.0E+9 N/m时各支撑轴承节点的冲击响应曲线

图9 隔振器刚度为2.0E+8 N/m时各支撑轴承节点的冲击响应曲线

图10 隔振器刚度为2.0E+7 N/m时各支撑轴承节点的冲击响应曲线
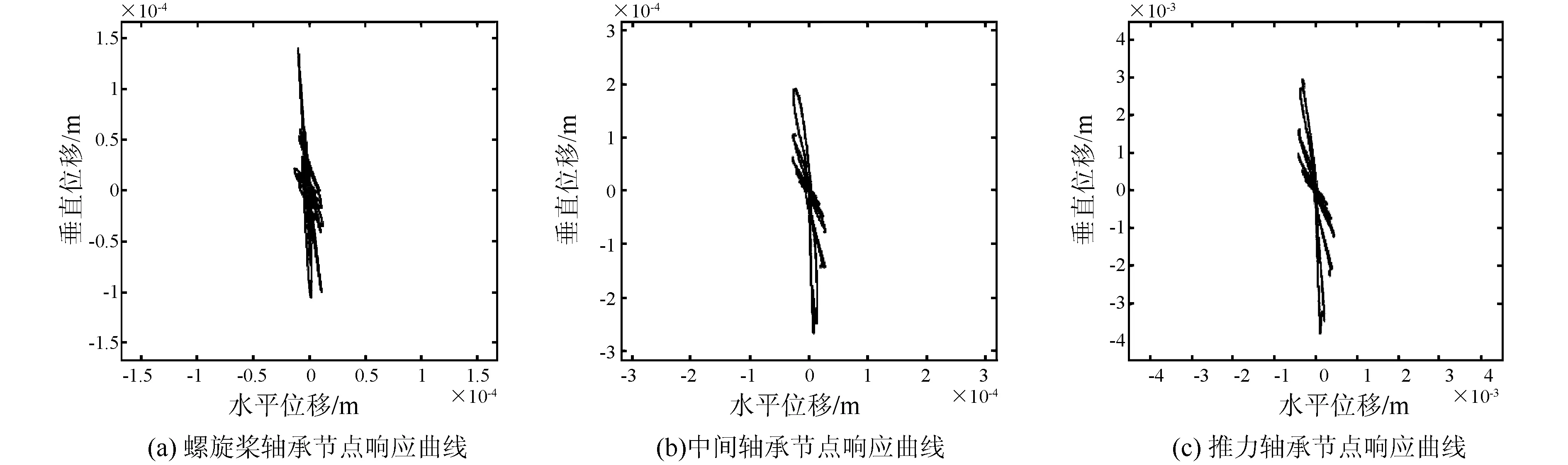
图11 隔振器刚度为2.0E+6 N/m时各支撑轴承节点的冲击响应曲线
需要特别说明的是,隔振器的刚度值具有非线性特征[4-5],冲击时的实际值应比静刚度值大,但由于没有试验数据,本文将其按照线性系统来处理。
上述的冲击响应计算可以说明下列一些基本特性:
1) 由于系统按照线性系统来计算,在冲击时间一定的条件下,基础冲击加速度的幅度越大,轴系的瞬态冲击响应的幅度也越大,冲击响应曲线的变化规律完全一致,不同之处
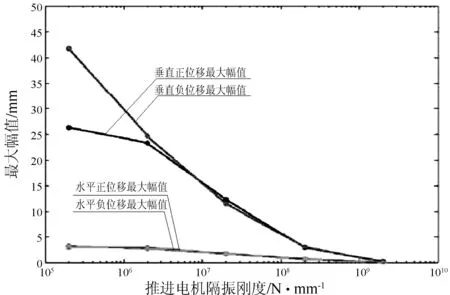
图12 轴系的最大正向振幅和负向最大振幅随隔振器刚度的变化
仅在响应的幅度上。
2) 轴系在冲击方向的瞬态响应远比在非冲击方向上的瞬态响应大。
3) 轴系受到基础冲击激励后的最大振幅随着主机隔振器的刚度按照指数规律迅速减小,为了减小基础冲击对整个轴系的影响,主机隔振器的刚度应选择得大一些。当然,如果能够保证隔振器具有相对大的阻尼效应,主机隔振器的刚度也可以选择得小一些。所以,在选择主机隔振器刚度时,必须对隔振器所能够提供的阻尼引起足够的重视。
5 结束语
在船舶主机隔振系统的设计中,隔振器刚度的选取是一个难点,其隔振性能与轴系的抗冲击性能存在互相抵触的一面,如何平衡两者之间的关系,是其设计的关键,应引起足够的重视。
[1] 汪玉,华宏星.船舶现代冲击理论及应用[M],北京:科学出版社,2005.
[2] 夸克工作室.有限元分析基础篇ANSYS与MATLAB[M].北京:清华大学出版社,2002.
[3] AHLIN K.Shock response spectrum calculation-an improvement of the small wood algorithm[C]:Proceedings of 70thShock and Vibration Symposium.New Mexico,USA,1999,11.
[4] 周文亮,王强,石理碧.隔振器冲击刚度的试验研究[J].噪声与振动控制,2003,23(6):15-17.
[5] 王基,朱石坚.V型橡胶减振器静刚度研究[J].噪声与振动控制,2003,23(1):37-40.
