初中数学例习题教学设计的反思

　　教育部颁发的《基础教育课程改革纲要》中要求，基础教育各门课程在目标设置上，要注重密切联系学生的生活和经验以及社会、科技发展的现实，把结果性目标与过程性目标、体验性目标相结合，实现知识与技能、过程与方法、情感态度与价值观的统一。因此，各门学科的教学都应该以此为标准进行设计。
　　就初中数学而言，例习题教学是初中数学教学中重要的组成部分，是概念类教学的延伸和发展。教材中的例习题都是编者精心筛选的，具有典型性和启发性，它们不仅是对基础知识的巩固，同时对培养学生智力、掌握数学思想和方法，以及培养学生应用数学意识和能力，提高学生的数学素养等都有重要意义。所以，在例习题的教学设计时，教师应该注重反思，不能只简单地给出解题过程，而是要关注它的分析过程和思维过程，使学生逐步掌握分析问题的思维方法。
　　反思之一：在例习题教学设计中，教师应该注重数学思想、方法的传授、理解与掌握。
　　日本著名数学教育家米山国藏认为，学生在学校学到的许多数学知识，如果毕业后没有机会去用的话，不到一年就忘掉了；唯有深深铭刻在头脑中的数学精神、数学思想、研究方法、推理方法等，却时刻发生作用，终生受益。因此，数学思想和方法对人才的培养及人的一生影响非常重要。初中数学有许多常用的、重要的数学思想方法，如转化与化归、猜想与验证、类比、分类讨论、方程与函数、换元、整体、数形结合等等。这些数学思想方法，教师在进行教学设计时，就应加以充分重视，结合具体情境，使学生明确其方法及应用。
　　例1.解方程：
　　
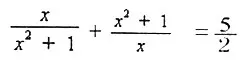
　　在这个方程中，如直接去分母，会得到一个次数高于二次的整式方程，不易求解；但由于互为倒数，故可把它们看成一个整体来进行，通过“换元”的方式就可以巧妙地把这道题解出来了。在教学过程中，可先让学生按常规方法将分式方程转化为整式方程来求解，然后引导学生通过观察，发现其中的代数式之间互为倒数的关系，把它们看成一个整体来进行解题。这样，学生既弄清了“换元”的意义、方法，又通过实例体会“换元”的作用，突出“换元”这种数学思想、方法的重要，学生理解、掌握了数学思想和方法，能达到融会贯通，举一反三之效。
　　反思之二：在例习题教学设计中，教师应该注重数学思维活动过程及方法的指导。
　　在数学例习题的教学设计中，教师不能仅仅只注重结果，把解题过程和盘托出，而应该注重数学思维活动过程的分析及数学思维方法的指导。通常可以从数学知识的发现过程、数学思维的发生过程、方法的探索过程、问题的分析解决过程等几方面去进行。
　　例2.某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽量减少库存，商场决定采取适当的降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天多售出2件，当降价多少元时，商场每天获得的利润最大？
　　此问题涉及到三个量，即利润、降价、销售量，商场每天获得的利润受价格、销售量的影响，在其中起关键作用的因素是降价，利润随降价幅度的变化而变化，由此可联想到建立函数模型，将实际问题抽象成数学问题。
　　面对实际问题，有时学生不知如何把实际问题转化成数学问题。教师在例题教学中，就应该把怎样思考、为什么这样思考的路径展示给学生，对数学知识的发现、概括及应用过程进行揭示和阐释，引导学生积极思维，达到不仅知其然，更知其所以然。当然，教师在教学过程中，也要充分启迪学生的思维，通过巧设“空白”，给予学生更多的思维空间，让学生去“发现”，去“创新”，让学生在思维活动过程中体会到问题解决的整个过程，真正提高分析问题的能力，掌握解决问题的方法；要为他们提供观察、操作、思考、探索、表达的机会，并在学生思维受阻时，给予必要的方法指导，保证学生思维的顺利进行。
　　反思之三：在例习题教学设计中，教师应该注重变式训练，提高基础知识的运用能力。
　　教师在例习题教学设计中，根据实际情况恰当地对题目进行不同的求解、延伸、演变、拓展，适时地创造悬念，通过变式练习， 使学生思维处于积极状态，开拓思路，提高运用基础知识的能力。教学中常用的方法有以下两种。
　　1.条件或结论适当改换或互换
　　通过这种方法，不仅使学生牢固地掌握了所学的知识，理解了例习题目中条件与结论之间的逻辑关系，而且能够引导学生把相关的知识点有机地链接起来，形成良好的知识结构，促进学生分析能力与思维能力的发展。
　　例3.已知正三角形的边长为a，求它的内切圆与外接圆组成的圆环的面积。
　　变式练习一：将此例中的“正三角形”改为“正方形”，圆环的面积是多少？
　　变式练习二：如果改成“正多边形”，圆环的面积是多少？观察你所计算的结果，你发现了什么？
　　2.条件或结论开放
　　
　　例4.如图，可以利用刻度尺和三角板测量圆形工件的直径，说明测量的理由。
　　这样的习题，我们可以把它改换为：根据所学知识，请你设计几种测量圆形工件直径的方法。此题改换成开放题后，学生就能通过做题，使其思维积极地发散，这样既考查了学生综合运用知识的能力，也考查了学生的思维品质。
　　除此之外，还有“一题多解”、“结论引申”等方法，都可以在例习题教学设计中很好的加以运用。总之，对于例习题采取不同方法的变式设计，能开阔学生思维，有利于知识的迁移和能力的培养，有利于学生良好思维品质的培养和形成。
　　（作者单位：安徽省寿县石集初中）