基于四元数分数阶广义拉盖尔图像矩的空间域零水印算法

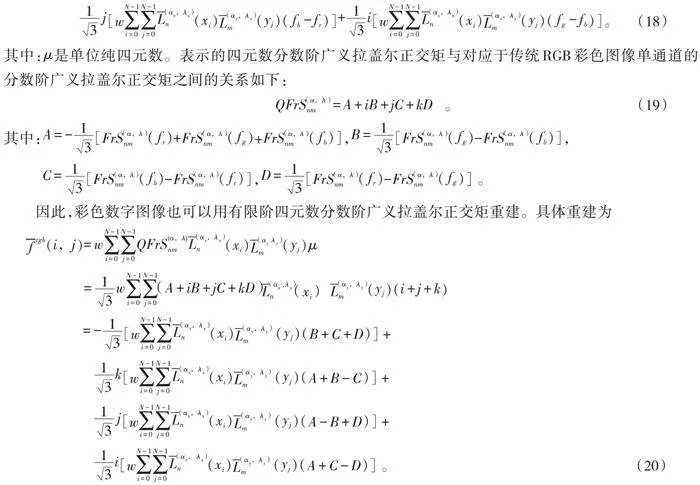
摘" " 要：现有的基于空间域零水印算法缺乏图像内容信息丢失检测的能力，特别是当图像遭受大面积裁切、随机涂抹或图像行列移除等攻击，水印提取算法就会失效。为了提高零水印算法抵抗图像遭受大面积裁切攻击的鲁棒性，提出一种基于四元数分数阶广义拉盖尔图像矩的空间域零水印算法。首先介绍分数阶广义拉盖尔多项式，其次构建四元数分数阶广义拉盖尔矩及不变量，最后设计彩色图像零水印算法。实验结果证明，所提出的零水印算法对常见的几何变换攻击具有一定的鲁棒性，同时对于滤波、有损压缩，特别是对图像大尺度剪切攻击具有较好的检测能力。

关键词：四元数；拉盖尔多项式；零水印；鲁棒性

中图分类号：TP391" " " " 文献标志码：A" " " " "文章编号：1009-5128（2025）02-0087-08

信息化及人工智能时代，数字图像数据很容易被盗用和篡改。因此，图像内容的数字版权保护是保护作者知识产权的关键性问题。［1］数字水印被认为是一种重要的版权保护技术，通过在图像中嵌入数字水印（或消息）来实现。水印嵌入宿主图像中，同时还需具有不可见性及鲁棒性。目前，在数字水印领域，许多学者和研究人员都专注于零水印的研究。［2–5］近年来，零水印技术解决了传统水印技术的不可见性和鲁棒性之间的矛盾，成为信息安全领域的研究热点。温泉等［6］于2003年首次提出零水印的概念，此后，零水印的研究受到越来越多学者的关注，许多相关的研究成果被应用于数字版权保护领域。

正交矩作为一种有效的图像描述子，在图像重建、数字图像水印和目标识别等图像处理和分析领域得到广泛应用。［7–9］正交矩包括连续正交矩和离散正交矩，其中连续正交矩如泽尼克矩、正交傅里叶-梅林矩和贝塞尔-傅里叶矩；离散正交矩如克劳丘克矩、切比切夫矩和哈恩矩。由于图像本身是数字化的，没有数值近似操作，因此，与连续正交矩相比，离散正交矩具有更好的数值稳定性。在图像处理和分析领域，彩色图像能够比灰度和二值图像包含更多的信息。基于四元数代数的彩色图像表示方法将图像视为描述彩色图像各个分量的三维向量，可有效利用彩色图像不同通道的颜色信息。［10］因此，对于彩色图像，可以使用四元数代数来构造四元数图像矩。研究人员通过现有的正交多项式构造出许多四元数图像矩，如四元数极谐-傅里叶矩（QPHFMs）、四元数指数傅里叶矩（QEFM）、四元数泽尼克矩（QZMs）等。为了对图像进行更加稳定和准确的描述，相关学者将整数阶图像矩扩展到分数阶，并提出相关的分数阶正交矩，如分数阶切比雪夫矩（Fr-CMs）、分数阶正交傅里叶-梅林矩（Fr-OFFMs）、分数阶泽尼克矩（Fr-ZMs）和分数阶通用雅可比傅里叶矩等。

本文基于四元数分数阶广义拉盖尔矩（QFr-GLOP）和Radon变换旋转角度检测算法提出一种新的零水印方案，并将其应用于彩色图像的数字版权保护之中。利用QFr-GLOP具有局部特征提取的特性来抵抗图像传输过程中所遭受的大规模裁切和涂抹攻击。另外，由于引入四元数方法，相比基于灰度和单通道的零水印方案，本文所提出的零水印方案在抵抗几何和传统图像处理攻击方面的性能更优。

1" "四元数分数阶广义拉盖尔矩及不变量

1.1" "广义拉盖尔正交多项式

广义拉盖尔正交函数或多项式（简称GLOP）可表示为[L（α）n]（[x]）。当[αgt;-1]时，在区间［0，[+∞]）上满足以下正交关系

[0+∞exp] （[-x]）[xαL（α）n]（[x]）[L（α）m]（[x]）[dx=Γ（n+α+1）n！δnm]。" " " " " " " " " " " " " " " " " " " （1）

设[w（α）]（[x]）[=exp]（[-x]）[xα]为加权函数，[Γ（n+α+1）n！=γ（α）n]为加权归一化系数，[Γ（·）]为伽马函数，则上述方程可修改为

[0+∞w（α）]（[x]）[L（α）n]（[x]）[L（α）m] （[x]）[dx=γ（α）nδnm]" 。" " " " " " " " " " " " " " " " " " " " " （2）

其中：[δnm]是Kronecker函数；[L（α）n]（[x]）可以表示为

[L（α）n]（[x]）[=（α+1）nn！1 F1]（[-n]，[α+1]；[x]）。" " " " " " " " " " " " " " " " " " " " " " " " " " "（3）

其中：（[α]）[k=α] [（a+1）]" [（a+2）][ …（a+k-1）]是Pochhammer函数；[1F1]（[-n]，[α+1]；[x]）是一个超几何函数，可以表示为

[1F1]（[a]，[b]；[z]）[=1+abz+a（a+1）z2b（b+1）2！+…=k=0∞（a）k（b）kzkk！]" 。" " " " " " " " " " " " " " " " "（4）

结合式（3）和（4），GLOP被重新定义为

[L（α）n]（[x]）[=][k=0n（-1）" k（n+α）！（n-k）！（k+α）k！xk]" 。" " " " " " " " " " " " " " " " " " （5）

为了便于计算，GLOP可以通过以下递归算法实现

[nL（α）n]（[x]）[=]［2（[n-1]）[+α+1][-][x]］[L（α）n-1]（[x]）[-]（[n-1+α]）[L（α）n-2]（[x]）。" " " " " " " " " " " "（6）

GLOP初始化的前两个多项式分别是[L（α）0]（[x]）[=1]和[L（α）1]（[x]）[=1+α-x]。

1.2" "分数阶广义拉盖尔正交多项式

分数阶广义拉盖尔正交多项式（Fr-GLOP）可表示为

[L（α，λ）n]（[x]）[=L（α）n]（[xλ]）" 。" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " "（7）

其中：[λgt;0，x∈]［0，[+][∞]），Fr-GLOP在［0，[+][∞]）上满足以下正交性

[0+∞w（α，λ）]（[x]） [L（α，λ）n] （[x]）[L（α，λ）m] （[x]）[dx=γ（α，λ）nδnm]" 。" " " " " " " " " " " " " " " " （8）

其中：[w（α，λ）]（[x]）[=λx（α+1）λ-1exp]（[-xλ]），[γn（α，λ）=Γ（n+α+1）n！]。

根据二项式展开形式，Fr-GLOP可表示为

[L（α，λ）n] （[x]）[=nψnixλi]。" " " " " " " " " " " " " " " " " " " " " " " " " " " " " "（9）

其中：[ψni=]（[-1]）[i] [Γ（n+α+1）Γ（i+α+1）" " " " " " " " " " " ]。

Fr-GLOP也可以通过以下递归方法实现：

[nL（α，λ）n]（[x]）[=]［2（[n-1]）[+α+1-xλ]］[L（α）n-1]（[x]）[-]（[n-1+α]）[L（α，λ）n-2]（[x]）。" " " " " " " " " " " "（10）

其中：[L（α，λ）0]（[x]）=1，[L（α）1]（[x]）=1+[α-][xλ]。

为了提高多项式在实际应用中的稳定性，通常使用归一化多项式来代替常规多项式。因此，归一化分数阶广义拉盖尔正交多项式定义如下

[L（α，λ）n] （[x]）=[L（α，λ）n]（[x]）[w（α，λ）（x）γ（α，λ）n] 。" " " " " " " " " " " " " " " " " " " " " （11）

归一化分数阶广义拉盖尔正交多项式在区间［0，+[∞]）上满足以下正交关系

[0+∞L（α，λ）n]（[x]）[L（α，λ）m]（[x]）[dx=δnm]。" " " " " " " " " " " " " " " " " " " " " " " （12）

考虑到计算复杂性和数值稳定性，归一化分数阶广义拉盖尔正交多项式的计算过程可以通过以下递归算法实现

[L（α，λ）n] （[x]）[=]（[AO+A1xλ]）[L（α，λ）n-1]（[x]）[+A2L（α，λ）n-2]（[x]） 。" " " " " " " " " " " " " " " " " "（13）

其中：[L（α，λ）0]（[x]）[=][w（α，λ） （x）Γ（α+1）]，[L（α，λ）1]（[x]）=（[1+α-xλ]）[w（α，λ）（x）Γ（α+2）]；[AO=2n+α-1n（n+α）] ， [A1=-1n（n+α）]，[A2=-（n+α-1）（n-1）n（n+α）] 。

1.3" "加权径向归一化分数阶广义拉盖尔正交多项式

加权径向归一化分数阶广义拉盖尔正交多项式具体形式为

[L（α，λ）n] （[r]）[=1rL（α，λ）n] （[r]） 。" " " " " " " " " " " " " " " " " " " " " " " " "（14）

加权径向归一化分数阶广义拉盖尔正交多项式在区间［0，+∞）和极坐标空间中满足以下正交性关系

[0+∞L（α，λ）n]（[r]） [L（α，λ）m] （[r]）[rdr=δnm] 。" " " " " " " " " " " " " " " " " " " " " " " （15）

1.4" "四元数分数阶广义正交拉盖尔矩

笛卡尔坐标系中灰度图像的分数阶广义拉盖尔正交矩可以定义为

[FrS （α，λ）nm=wN-1N-1fg]（[i，j]）[L（αx，λx）n] （[xi]） [L（αy，λy）m]（[yj]）。" " " " " " " " " " " " " " " " "（16）

其中：[fg]（[i]，[j]）表示二维数字图像。

为了便于计算，可以将原始二维图像数字矩阵映射到［0，[L]］[×]［0，[L]］的正方形区域。在这里， [Lgt;0]，

[w=（L∕N） 2]，[xi=iLN]，[yi=jLN]，" [i，j=0]，1，2，…，[N-1]。

根据四元数理论，可以在RGB颜色模型空间中使用纯四元数代数表示彩色图像，如

[f（rgb）]（[x，y]）[=fr]（[x，y]）[i+][fg]（[x，y]）[j+fb]（[x，y]）[k]，" " " " " " " " " " " " " " " " " " " "（17）

则笛卡尔坐标系中RGB彩色图像的右侧四元数分数阶广义拉盖尔正交矩（QFr-GLOM）定义如下：

[QFrS （α，λ）nm=wi=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）[frgb]（[i，j]）[μ]

[=13wi=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）（[ifr+jfg+kfb]）（[i+j+k]）

[=-13wi=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）（[fr+fg+fb]）[+13k]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）（[fr-fg]）］[+]

[13j]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）（[fb-fr]）］[+13i]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m]（[yj]）（[fg-fb]）］。" " "（18）

其中：[μ]是单位纯四元数。表示的四元数分数阶广义拉盖尔正交矩与对应于传统RGB彩色图像单通道的分数阶广义拉盖尔正交矩之间的关系如下：

[QFrS（α，λ）nm=A+iB+jC+kD]" "。" " " " " " " " " " " " " " " " " " " " " " " " "（19）

其中：[A=-13]［[FrS（α，λ）nm]（[fr]）[+FrS（α，λ）nm]（[fg]）+[FrS（α，λ）nm]（[fb]）］，[B=13]［[FrS（α，λ）nm]（[fg]）[-FrS（α，λ）nm]（[fb]）］，

[C=13]［[FrS（α，λ）nm]（[fb]）[-FrS（α，λ）nm]（[fr]）］，[D=13]［[FrS（α，λ）nm]（[fr]）[-FrS（α，λ）nm]（[fg]）］ 。

因此，彩色数字图像也可以用有限阶四元数分数阶广义拉盖尔正交矩重建。具体重建为

[frgb]（[i，j]）[=wi=0N-1j=0N-1QFrS（α，λ）nmL（αx，λx）n]（[xi]）[L（αy λy）m]（[yj]）[μ]

[=13wi=0N-1j=0N-1（A+iB+jC+kD）][L（αx ，λx）n（xi） L（αy，λy）m]（[yj]）（[i+j+k]）

[=-13]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m] （[yj]）（[B+C+D]）］ [+]

[13k]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m] （[yj]）（[A+B-C]）］ [+]

[13j]［[w][i=0N-1j=0N-1L（αx，λx）n]（[xi]）[L（αy，λy）m] （[yj]）（[A-B+D]）］ [+]

[13i]［[w][i=0N-1j=0N-1L（αx， λx）n]（[xi]）[L（αy，λy）m] （[yj]）（[A+C-D]）］ 。" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " （20）

2" "几何不变量预处理框架

由于在不同坐标系中构造的正交矩不变量由不同的算法实现，我们假设原始正交矩（而不是不变矩）作为所提出的零水印系统中图像特征的描述子。为了公平比较并正确评估不同正交矩的图像描述能力，我们设计一个统一的几何不变量预处理框架，该框架可处理不同坐标空间中构建的图像矩。在此框架中，几何变形通过以下方法统一处理：

（1）旋转引起的几何变形由RTDO（Radon变换检测方法）来校正旋转角度，然后计算图像矩。

（2）通过计算几何矩、在图像质心处设置坐标系原点以及计算图像矩来校正平移引起的几何失真。

（3）通过对图像进行尺度归一化，然后提取矩特征来校正由尺度引起的几何变形。

3" "零水印注册及检测算法设计

3.1" "零水印注册算法设计

算法通过以下步骤进行：

步骤1：将需要版权保护的原始彩色宿主图像分成W×W块。为了保持图像的细节并降低数字水印中的虚警率，图像中分割的块图像的大小不应太小。根据经验，块图像的大小应超过原始图像大小的1/9。在本文中，彩色宿主图像[I（RGB）M×N]的大小为192×192。因此，将原始图像分成3×3块，并将分割的图像标记为[B（RGB）k]。

步骤2：提取每个块图像对应的彩色主图像的局部特征参数（即[αx，][ αy，][ λx，] [λy]和[L]），并将其设置为关键字符序列[keyi=αix，] [αiy，] [λix，] [λiy，] [Li]，[i=]1，2，…，9，然后提取所提出的QFr-GLOM的多个低阶矩作为特征向量[V（RGB）k]，[k=]1，2，…，9。这里设置[V（RGB）k=]｛[v（1）nm，v（2）nm，…，v（k）nm，k=9]｝，此特征向量在证书颁发机构中心（CA中心，第三方版权保护中心）注册。

步骤3：上述信息带有时间戳，并与用户的签名信息一起在CA中心注册。此时，原始彩色主机图像被宣布受到版权保护。

3.2" "零水印检测算法设计

水印的正确检测或提取是数字水印系统设计中的关键问题。现有的传统水印检测系统在通过信号处理操作（例如主图像的强裁切或涂抹）丢失之后不能正确地提取或检测水印。因此，本文提出一种有效抵抗信息丢失和几何攻击的水印检测方案。实现步骤如下：

步骤1：如果版权认证的宿主彩色图像受到旋转变换的攻击，则通过Radon变换检测方法校正旋转角度，并执行下一操作。否则，直接执行步骤2。

步骤2：完成彩色主机图像的缩放标准化。缩放归一化通常通过以下两种方法之一来执行：（1）将彩色图像映射到笛卡尔坐标系中的正方形区域，（2）在执行插值操作的同时将彩色图像的大小缩放为固定大小的模板。在本文中，图像通过第二种方法进行归一化：让彩色图像[f（RGB）]（[x]，[y]）成为缩放操作之后的目标图像。通过[f（RGB）（x，y）=As]［[f（RGB）]（[x]，[y]）］获得[f（RGB）]（[x]，[y]），其中[f（RGB）]（[x]，[y]）是缩放图像，[As]是变换矩阵

[As=]［[μ00v]］ 。" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " "（21）

在此矩阵中，参数[μ]和[v]分别表示图像矩阵中行和列的缩放因子。图像处理或模式识别也需要插值操作，不同的插值方法会影响缩放图像的视觉质量。基于MATLAB的仿真环境，在[μ≥0.5，v≤1]时采用双线性插值，在[μ≥0，] [v≤0.5]或[μ，] [v≥2]时采用双三次插值。

步骤3：此步骤执行平移。首先，从彩色图像[f（RGB）]（[x]，[y]）计算几何矩[M（RGB）" pq]（[x]，[y]），这些矩指定图像重心的坐标位置：[xa=x-M（RGB）10M（RGB）00，ya=y-M（RGB）01M（RGB）00]。其次，将图像[f（RGB）]（[x]，[y]）转换为[f（RGB）]（[xa]，[ya]）。最后，获得中心化彩色图像。

步骤4：在处理旋转、缩放和平移步骤之后，通过水印注册方案中的步骤1和2处理彩色图像，从而获得新的特征向量[V（RGB）k，] [k=1，] [2]，[…，] [9]。

步骤5：从CA中心提取特征向量[V（RGB）k]，并将在前一步骤中获得的特征向量[V（RGB）k]与在零水印算法的注册阶段获得的特征向量[V（RGB）k]之间的绝对差相加。总额计算如下：

[d=min]｛[1cnt2n=1cntm=1cnt]│[v（k）nm-v（k）nm]│｝。" " " " " " " " " " " " " " " " " " " "（22）

在本实验中，[cnt=10]和[k=1，] [2]，[…，] [9]。当[d≥ε]（其中[ε]是经验阈值，在当前实验中设置为0.02）且时间戳与CA中心提供的信息不匹配时，验证完成，证明水印不存在；否则证明彩色宿主图像包含水印信息。

4" "仿真实验及结果分析

为了验证所提出的QFr-GLOM的零水印算法的有效性，从COIL-100数据库中选择“cat”彩色图像作为原始图像，并将其大小归一化为192[×]192。大小归一化图像被作为宿主图像（如图1所示）并给出了两组实验结果及分析。第一组实验研究本文提出的算法对各种信号处理和几何攻击的鲁棒性。第二组实验检验所提出的零水印算法在强裁切和随机涂抹图像上的性能，并可视化了cat宿主彩色图像上不同裁剪和涂抹比例的结果。通过PSNR测量原始彩色宿主图像和攻击彩色图像之间的相似度，并且通过式（22）判断检测到的特征向量[V（RGB）k]和CA中心中的特征向量之间的相似度。显然，越接近0，零水印方案鲁棒性越强。

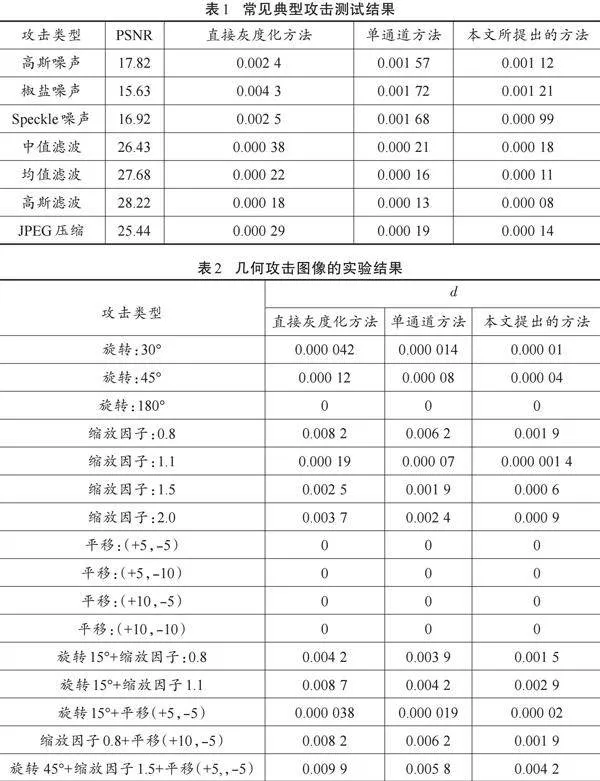
实验1：在网络传输过程中，图像极易受到噪声干扰。在该实验中，原始彩色宿主图像在方差为0.02的高斯白噪声、密度为5%的椒盐噪声和方差为0.04的斑点噪声的攻击下进行了测试。由于噪声干扰通常通过滤波操作来消除，滤波是图像处理和模式识别中另一个经常遇到的攻击。在实验中，用一个窗口对原始彩色宿主图像进行中值和平均滤波。此外，计算机视觉或信号处理中的图像经常通过模糊和JPEG压缩来处理。图像模糊导致部分块失真，JPEG压缩导致像素丢失。在这个实验中，在Matlab 2023a软件环境中，高斯模糊参数被设置为默认值，JPEG压缩比被设置为60。

表1比较了所提出的零水印方案和其他方案（基于直接灰度的方法和基于单信道的方法）的结果，所提出的算法具有较强的鲁棒性，并且优于已有的两种方案。彩色宿主图像上最常见的几何攻击是旋转、缩放和平移。这些攻击改变了图像中的像素位置，增加了水印检测的难度。在抗旋转实验中，将宿主彩色图像旋转30°，45°和180°。在抗缩放实验中，缩放参数变化为0.8，1.1，1.5和2.0。转换参数如表2所示。在某些情况下，彩色宿主图像受到组合几何攻击，例如旋转+缩放、旋转+平移、缩放+平移和旋转+缩放+平移攻击，彩色宿主图像经受组合几何攻击的结果如表2所示。将本文的算法和现有方案的实验数据进行比较，可以发现所提出的方案总体性能优于其他方法。

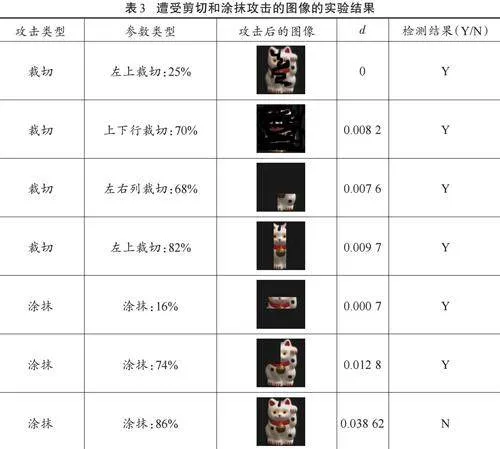
实验2：裁切或涂抹攻击是数字水印中最困难的问题。尽管现有的数字水印算法对小规模裁切和涂抹操作具有鲁棒性，但大多数算法在大规模裁切或涂抹操作下都会失败。在这个实验中，彩色宿主图像在图像的不同区域以不同的比例（25%，70%，68%，82%，）进行裁切，也以16%，74%和86%的比例随机涂抹。表3显示了裁切的图像及其实验结果。结果表明：本文所提出的基于QFr-GLOM的方案能够有效地检测到水印，即使在裁切了82%的图像上也是如此。因此，所提出的方案适用于裁切或涂抹图像的真实图像版权保护。

5" "结语

本文提出了一种针对彩色图像版权保护的优化空间域零水印方案，该方案依托QFr-GLOM图像矩技术，对传统图像处理操作具有高度的鲁棒性，具体包括噪声干扰、平滑滤波攻击，特别是大规模裁切与涂抹攻击等，从而在彩色图像版权保护领域展现出重要的实际应用价值。对于未来的研究方向，将专注于探索与彩色图像紧密相关的其他领域，涵盖图像检索、图像分类、图像匹配及其他相关科研范畴。

参考文献：

［1］" 李吕牧之.基于区块链和零水印的数字图像版权保护研究［D］. 唐山：华北理工大学，2023.

［2］" 林荣胜，柯逍.一种快速的零水印印刷品信息隐藏方法［J］.计算机仿真，2023（4）：189-194.

［3］" 戴夏菁，徐谊程，王馨娅，等.基于Word2Vec的中文文本零水印算法［J］.软件工程，2023（1）：19-23.

［4］" 周绶泉，咸雯雯，石慧.基于多特征和混沌加密的零水印算法［J］.计算机系统应用，2022（12）：147-158.

［5］" 徐依朋，胡坤，王小超，等.基于BEMD和DFT的遥感图像零水印算法［J］.计算机辅助设计与图形学学报，2022（11）：1731-1741.

［6］" 温泉，孙锬锋，王树勋.零水印的概念与应用［J］.电子学报，2003（2）：214-216.

［7］" HOSNY K，DARWISH M.Invariant color images representation using accurate quaternion Legendre-Fourier moments［J］.Pattern Analysis and Applications，2019，22（3）：1105-1122.

［8］" 徐丽云，张敏.极谐波分数傅里叶矩及其零水印算法应用［J］.小型微型计算机系统，2023（4）：1-9.

［9］" LIU Y，ZHANG S，LI G，et al.Accurate quaternion radial harmonic Fourier moments for color image reconstruction and object recognition［J］.Pattern Analysis and Applications，2020（7）：1-17.

［10］" HE B，LIU J，LIN G C，et al.Quaternion Fractional-order weighted generalized Laguerre-Fourier moments and moment invariants for color image analysis recognition［J］.Signal Processing：Image Communication，2023，114：116941.

【责任编辑" " 牛怀岗】

On Spatial Domain Zero Watermarking Algorithm Based on Quaternion Fractional-Order Generalized Laguerre Image Moments

WANG Jing， JIA Xiaoqiang

（School of Computer Science and Technology， Weinan Normal University， Weinan 714099， China）

Abstract：The existing spatial domain zero-watermarking algorithms lack the capability to detect loss of image content information， especially when images suffer from large-scale cropping， random scribbling， or row and column removal attacks， it can cause the watermark extraction algorithm to fail. To enhance the robustness of zero-watermarking algorithms against large-scale cropping attacks on images， this paper proposes a spatial domain zero-watermarking algorithm based on quaternion fractional-order generalized Laguerre image moments. Firstly， the paper introduces fractional-order generalized Laguerre polynomials； secondly， it constructs quaternion fractional-order generalized Laguerre moments and invariants based on these polynomials； finally， it designs a color image zero-watermarking algorithm based on the constructed invariants. Experimental results demonstrate that the proposed zero-watermarking algorithm has a certain level of robustness against common geometric transformation attacks and exhibits good detection capabilities for filtering， lossy compression， and particularly for large-scale image cropping attacks.

Key words：Quaternion； Laguerre polynomial； zero watermark； Robustness

基金项目：陕西省体育局资助项目：智能图像处理及数字版权保护在竞技体育中的应用研究（20240371）；渭南师范学院科学研究计划人才项目：分数阶正交图像矩及其在图像检测中的关键技术研究（2021RC19）；渭南师范学院科学研究计划人才项目：基于超复数分数阶矩的鲁棒性数字图像零水印算法研究（2023RC01）

作者简介：王晶，女，山东德州人，渭南师范学院计算机学院讲师，信息学博士，主要从事数字版权保护、图像水印、人工智能教育研究。