弹塑性接触冲击永久变形与滑移长度的解析求解

摘要：在机械系统的设计与应用中，多体表面之间的弹塑性接触冲击现象是一个重要的力学问题，蕴含复杂的物理力学特性，对接触力等关键参数的解析与表征还存在许多争议与谜团。针对弹塑性倾斜接触冲击事件，根据Brake压陷模型建立瞬时接触力和接触变形的计算式，用接触变形系统地探讨与描述弹塑性接触冲击过程；基于广义动量定理，对冲击持时、永久变形和滑移长度的内在关系进行解析，分别得到以积分形式表示的永久变形和滑移长度表达式，再结合已发表文献中冲击对象在接触冲击前后的运动试验数据进行解析求解；测量接触冲击后被冲击对象的变形区域并进行对比分析。试验与数值结果表明：采用广义动量定理所建立的方法求解永久变形和滑移长度，其计算结果与试验值吻合较好，与采用Brake压陷模型直接积分数学方程相比，该方法计算结果更准确。

关键词：弹塑性；倾斜冲击；冲击持时；永久变形；滑移长度

中图分类号：O343.3；TB122

DOI：10.3969/j.issn.1004132X.2024.08.006

开放科学（资源服务）标识码（OSID）：

Analytical Solution of Permanent Deformations and Sliding Lengths

during the Elasto-plastic Oblique Contact-impacts

WANG Yao1 GUAN Enguang1 ZHANG Qinglei1， 2

1.College of Logistics Engineering，Shanghai Maritime University，Shanghai，201306

2.China（Shanghai） Institute of Free Trade Zone Supply Chain，Shanghai Maritime University，

Shanghai，201306

Abstract： For the design and applications of mechanical systems， the elasto-plastic contact impact phenomenon among the multi-body surfaces was one of the key mechanics problems， which contained complex physical and mechanics properties. There still were many controversies and mysteries regarding the analysis and characterization of key parameters such as contact force. For the elasto-plastic oblique contact-impact events， the calculated formulas of instantaneous contact forces and contact deformations were established based on the Brake indentation model， and the elasto-plastic contact impact process from the contact deformations was described systematically in detail. The internal relationship among impact duration， permanent deformation and sliding length was analyzed analytically based on the generalized momentum theorem， and the permanent deformations and sliding lengths expressed in the integral form were obtained respectively， and then， combined with testing data for the motions of the impact objects before and after contact impact reported in literatures， the analytical solution was obtained. The deformation region of the impacted object after the contact impact was measured， and the comparative analysis was also performed. The experimental and numerical results show that the calculated results of the permanent deformations and sliding lengths solved by using the approach developed by the generalized momentum theorem are found to be in good agreement with the experimental data. And this approach yields more accurate results compared to the direct integration of mathematical equations using the Brake indentation model.

Key words： elasto-plastic； oblique impact； impact duration； permanent deformation； sliding length

0 引言

对于机械系统的设计与应用，接触冲击（或碰撞）现象是一个重要的力学问题，普遍存在于机械装配或组件系统中［1-6］，如螺纹连接、轴承装配、凸轮或齿轮高副机构、车辆碰撞、航天器交会对接、机器人结构等。自1882年赫兹接触（Hertzian contact）理论提出以来［7］，接触冲击问题已经被研究了近一个半世纪，但由于相关接触冲击理论以及影响因素的复杂性［8-10］，学者和工程技术人员对这一问题的认识、理解及拓展依然有局限性。

接触冲击问题通常可描述为不同物体（两个或多体）表面之间的相互接触冲击所产生的复杂局部力学行为［11-12］，如恢复系数、接触区域、接触变形、接触力等，整个过程的冲击持时极短（量级为微毫秒），且伴随有复杂的非线性接触力变化和明显的冲击对象运动学参数变化；同时，这些变量参数又受到诸多因素的影响［13］，如初始条件、材料属性、几何形状、表面质量、应变硬化、摩擦振动等。从材料变形性能角度看，任何接触冲击事件可划分为三种状态：完全弹性、弹塑性和完全塑性。以金属表面之间的接触冲击为例［14-15］，完全弹性状态存在非常小的接触变形且可恢复，弹塑性状态则从接触表面下的某一深度开始（发生屈服），再过渡到完全塑性状态（部分接触变形可恢复），直到产生永久变形。实际上塑性状态可认为是弹塑性状态的一个极限，而完全塑性状态极有可能导致机械故障。因此，大多数接触冲击事件是存在于弹塑性状态的，这也是研究该问题最复杂的一个接触阶段。在弹塑性接触冲击模型的研究方面，主要可分为压陷模型和扁平模型两类，其主要区别在于接触冲击机理不同，前者是刚性冲击对象压入变形的被冲击对象中，代表模型如Brake模型［16］等；而后者是变形的冲击对象压在刚性被冲击对象上，代表模型如Jackson-Green模型［17］等。也有学者认为两个接触对象均发生变形，如Gheadnia模型［18］等；还有学者从阻尼角度建立了黏弹性/黏弹塑性模型［19］等。总体来说，针对不同的应用对象，各个模型所构建的表达式对弹塑性接触冲击的分析各有优劣，并且由于弹塑性状态下应力分布的复杂性以及接触变形与路径相关的依赖性，弹塑性状态没有封闭解。

对于弹塑性接触冲击问题，研究者主要关注接触冲击过程的运动学和动力学参数变化规律，如接触力、接触变形、恢复系数、摩擦类型等。其中，接触力与接触变形的变化规律由所建立的接触冲击模型决定；对于恢复系数［20］，常见的定义有运动恢复系数、泊松恢复系数、能量恢复系数等，均可通过接触力和冲击持时的组合，以冲量形式来建立其表达式，从而在运动学分析时，不必关注接触力瞬态变化的影响；对于倾斜接触冲击事件，摩擦因数起着重要的作用，在不同的初始倾斜角下，其摩擦类型是不同的，关系到冲击对象是否发生滑动摩擦，因此，滑移长度也是一个重要的表征参数。

本文以弹塑性材料为研究对象，针对弹塑性倾斜接触冲击事件，首先系统地探讨和描述其弹塑性接触冲击过程；然后将冲击持时、永久变形和滑移长度联系起来，基于广义动量定理建立彼此之间的内在关系，旨在得到永久变形和滑移长度这两个表征参数的解析表达式；在此基础上，再结合冲击对象在接触冲击前后的运动试验数据对其进行解析求解；最后采用OLYMPUS激光共聚焦扫描显微镜（CLSM）测量变形区的三维轮廓，对所建立的方法进行试验与数值结果对比分析，以验证解析模型的正确性。

1 弹塑性接触冲击

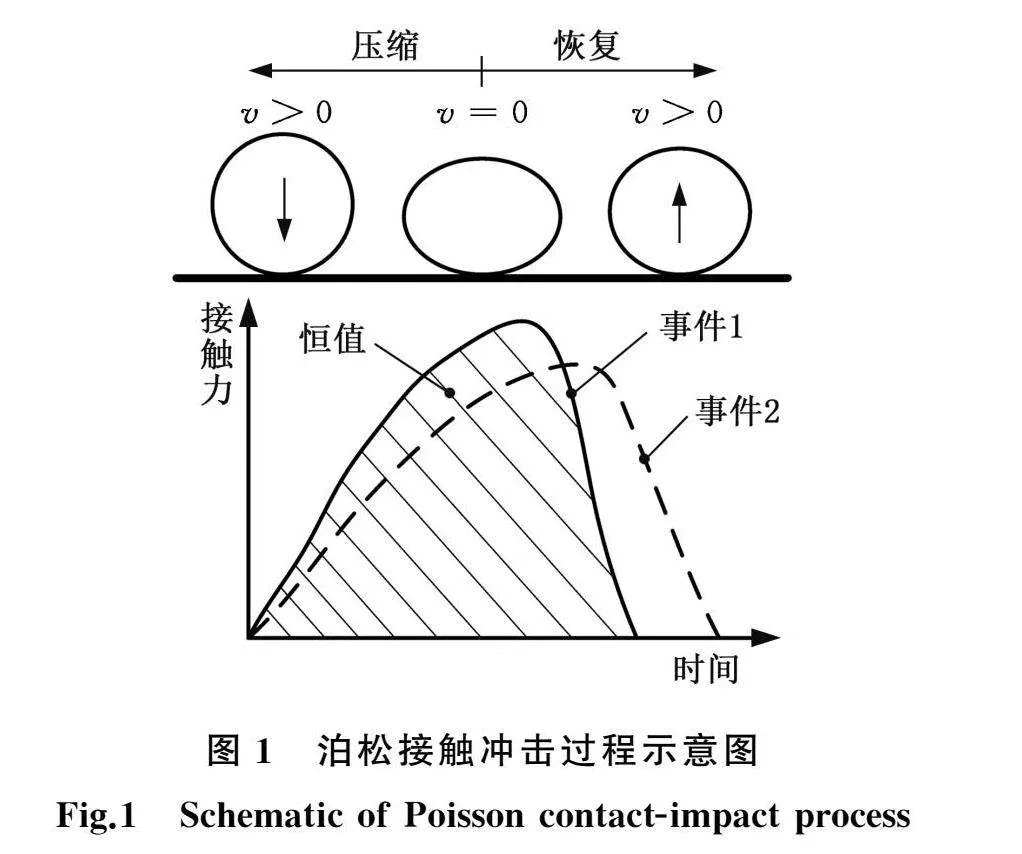
对于接触冲击问题，以球体垂直冲击大质量固体平面为例，根据泊松恢复系数的定义可将接触冲击过程分为压缩和恢复两个阶段。如图1所示，压缩阶段从冲击物体与被冲击物体相互接触开始，直到接触力达到最大值，此时压缩阶段结束、恢复阶段开始，而当接触力为零时，接触冲击结束。该接触冲击过程的描述实际上是关注了接触冲击之后的状态，即恢复系数（或冲量）是一个重要表征参数；由于恢复系数狭义上仅与碰撞物体的材料属性有关［21］，故其整个接触冲击过程的接触力冲量是近似恒值，即接触力时间曲线所围成的阴影面积。

从压陷或扁平接触模型分析［8-9，12-18］，接触冲击过程可分为弹性、弹塑性和恢复三个阶段。其中，弹性和弹塑性两个阶段为加载阶段，而恢复阶段为卸载阶段。如图2所示，弹性阶段从碰撞两物体发生接触冲击开始，直到两物体中的弱材料发生屈服为止，此时弹性阶段结束而弹塑性阶段开始；当冲击物体的接触点法向速度为零时，接触变形和接触力均达到最大值，此时弹塑性阶段结束而恢复阶段开始；在恢复阶段，部分接触变形将反向恢复，当接触力减小到零时，接触变形达到永久变形，接触冲击结束。该接触冲击过程的描述，实际上是关注了整个接触冲击过程中的状态，即接触力和接触变形是两个重要的表征参数。

本文考虑末端圆形杆件B倾斜冲击固体平面S的接触冲击事件。其中，杆件B和平面S是由弹塑性材料构成的研究对象，材质分别为20钢和巴氏合金（牌号ZSnSb11Cu6）；杆件B的尺寸参数：长度L、直径d，两端半球形圆头半径R=d/2；平面S的外形尺寸：长×宽×高为100 mm × 100 mm × 5 mm，表面粗糙度Ra不超过1.6 μm。

1.1 系统动力学模型

杆件B和平面S组成了典型的杆件平面系统。图3为系统运动链示意图，固定坐标系为笛卡儿坐标系，对应正交基矢量为（i，j，k），倾斜冲击角为θ，杆件B质心为C，重力为G，接触点为E，接触力为F。根据力的分解运算，接触冲击过程中接触力的法向分量为Fn、切向分量为Ft。

根据图3所示固定坐标系，从杆件B接触冲击平面S开始，接触点E的位置向量可表示为

rE=xi+δj（1）

式中，x为接触点E的切向位移；δ为接触点E的法向位移，即接触变形，表示接触表面下的某一深度。

质心C的位置向量为

rC=［xi+（δ+R）j］+L－d2（－icos θ+jsin θ）（2）

杆件B的角速度向量和角加速度向量分别为

ω=θ·k" α=θ¨k（3）

对式（1）、式（2）分别求时间t的一阶导数，即可得到质心C和接触点E的速度向量：

vC=drCdt（4）

vE=vC+ω×（rE－rC）（5）

同理，对速度向量求时间t的一阶导数，即可得到质心C和接触点E的加速度向量：

aC=d2rCdt2（6）

aE=aC+α×（rE－rC）+ω×［ω×（rE－rC）］（7）

根据牛顿欧拉（Newton-Euler）方程，得到杆件B的运动方程：

maC=Fti+（Fn－G）j

ICα=（rE－rC）×（Fti+Fnj）（8）

G=mg" Ft=－μkFnvEi|vEi|

式中，m为杆件B的质量；IC为杆件B质心的转动惯量；g为重力加速度；μk为动摩擦因数。

对于初始接触冲击条件，杆件B属于自由落体运动，由质心C的初始坠落高度H决定。

1.2 弹塑性接触冲击

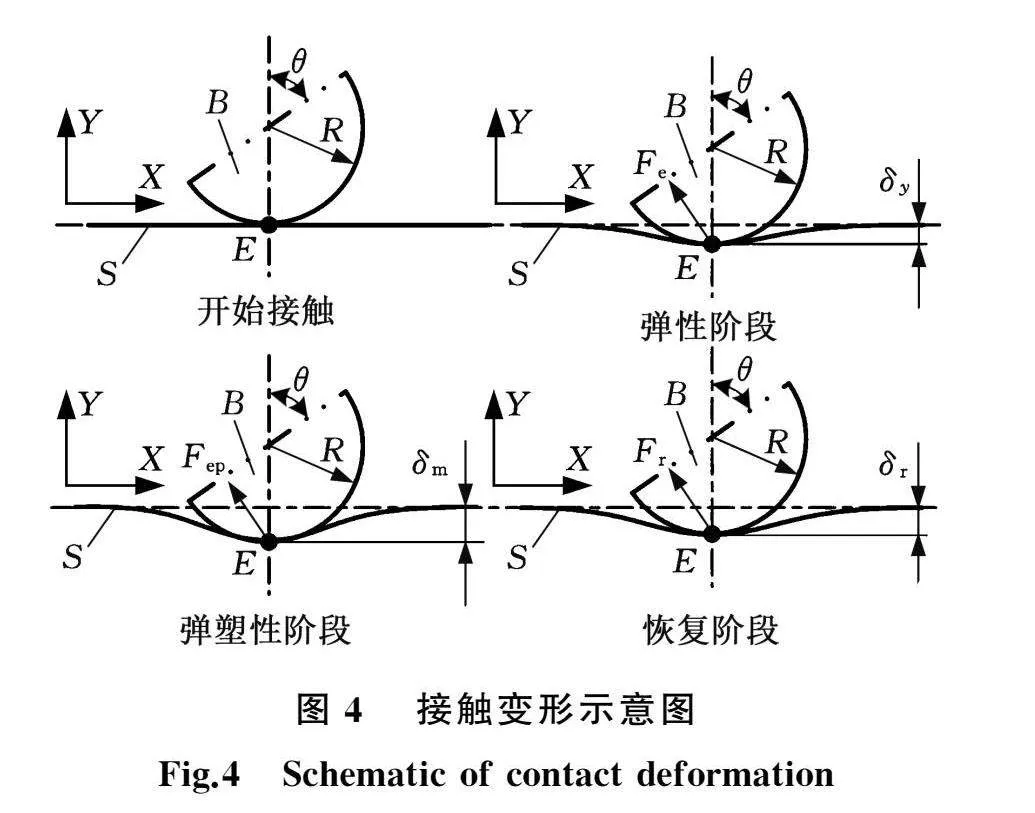
图4为接触变形示意图。从接触变形角度系统地探讨与描述弹塑性接触冲击过程各个阶段的变化规律并建立数学模型。用赫兹接触理论［7］分析弹性阶段和恢复阶段；基于Brake压陷模型［12，16，18，22］分析弹塑性阶段。

等效弹性模量E′和等效曲率半径R′分别为

1E′=1－μ2bEb+1－μ2fEf

1R′=1Rb+1Rf（9）

式中，Eb、Ef分别为杆件B和平面S的弹性模量；μb、μf分别为杆件B和平面S的泊松比；Rb、Rf分别为杆件B和平面S的半径。

由于Rb=R，Rf=∞，故R′=R。对于弹性阶段［7］，接触力Fe和接触半径a分别为

Fe=43E′R0.5δ1.5（10）

a=Rδ（11）

弹性阶段从杆件B与平面S发生接触开始，直到两碰撞物体中的弱材料发生屈服。根据von Mises屈服准则，屈服变形（即临界接触变形）δy为

δy=RFμ（πσy2E′）2（12）

Fμ=maxz≥0［－（μ+1）（1－zaarctanaz）+1.5a2a2+z2］2

式中，Fμ为应力场最大振幅；μ为碰撞两物体中弱材料的泊松比；z为接触表面之下的距离，即接触变形δ；σy为碰撞两物体中弱材料的屈服应力。

当δgt;δy时，弹塑性阶段开始，直到接触变形达到最大变形δm。Brake压陷模型［16，22］认为该阶段弹性效应从近场平滑过渡到远场，并且随着塑性区域的增大，弹性区域呈现衰减变化趋势。弹塑性阶段的接触力Fep和接触半径aep分别为

Fep=sech（（1+nε）δ－δyδp－δy）·43E′R0.5δ1.5+

（1－sech（（1－nε）δ－δyδp－δy））·p0πanan－2p（13）

aep=Rδ［2－sech（（1－nε）δ－δyδp－δy）］（14）

p0=106H′g" H′=（2Hb+2Hf）－1" nε=n－2

ap=［3p04E′2n/2πR（n－1）/2δ（n－3）/2］1/（n－2）

式中，nε为应变硬化指数；n为Meyer硬度指数［23］；δp为塑性变形；ap为塑性变形时的接触半径；p0为不考虑应变硬化且均布的接触压力；H′为等效布氏硬度；Hb、Hf分别为杆件B和平面S的布氏硬度。

恢复阶段从接触变形达到最大变形开始，直到发生永久变形δr，即不可恢复变形。对于恢复阶段［8，10，14-18，22］，假设没有反向屈服发生。在此阶段，其接触力Fr和接触半径ar分别为

Fr=43E′R0.5r（δ－δr）1.5（15）

ar=Rr（δ－δr）（16）

Rr=（3Fm4E′）2·1（δm－δr）3

δr=δm（1－3Fm4E′R0.5δ1.5m）

式中，Rr为恢复阶段的等效曲率半径；Fm为最大变形时的最大接触力。

1.3 直接积分数学方程

采用MATLAB的ODE45函数对上述模型进行数值求解，即可得到冲击持时、接触变形、接触力、杆件运动变量（如位置、速度、加速度、角度、角速度）以及恢复系数等参数的数值解。其中，永久变形δr和滑移长度Ls可通过接触点E的位置变化曲线获得，也可用直接积分数学方程来等价表示，即

δr=∫T0vEjdt（17）

Ls=∫T0vEidt（18）

式中，T为冲击持时。

2 解析求解方法

本文第一作者等的前期工作［8］中：基于数字图像处理方法，通过设计多标识点的冲击试验，描述与跟踪了冲击对象在接触冲击过程中的运动规律，即杆件B任意标识点的位置、速度及角速度变化曲线均可通过实验后处理求得。结合冲击对象在接触冲击前后的运动试验数据，基于广义动量定理对冲击持时、永久变形和滑移长度的内在关系进行解析分析，建立永久变形和滑移长度更为准确的解析求解方法。

在冲击持时T内，基于广义动量定理，可得

∫T0Fdt=m（vCf－vCi）（19）

式中，vCi、vCf分别为杆件B质心C接触冲击始、末速度。

如图3所示，令固定坐标系的原点与接触点E重合，则质心C的位置向量可表示为

rC=－L－d2icos θ+（L－d2sin θ+R）j（20）

设接触点E的初始冲击速度为

vE（t=0）=0i+vij（21）

式中，vi为接触点E的初始法向速度。

则在接触冲击过程中，质心C的速度向量为

vC=vij+1m∫t0Fdt（22）

将接触力进行分解运算，式（22）可改写为

vC=（1m∫t0Ftdt）i+（vi+1m∫t0Fndt）j（23）

设接触冲击过程中杆件B所受力矩为M，根据角动量定理，则杆件B的角速度可表示为

ω=1IC∫t0Mdt（24）

同理，将力矩M进行分解运算，结合式（20），式（24）可改写为

ω=1IC［L－d2cos θ∫t0Fndt－

（L－d2sin θ+R）∫t0Ftdt］k（25）

在接触冲击过程中，接触点E的速度向量为

vE=vExi+vEyj=vC+ω×rCE（26）

rCE=L－d2icos θ－（L－d2sinθ+R）j

接触冲击过程中的摩擦因数μ′可表示为

μ′=∫t0Fxdt∫t0Fydt=vCfi－vCiivCfj－vCij（27）

将式（23）、式（25）和式（27）代入式（26），化简后得

vEx=［（1m－1IC（L－d2sin θ+R）2）μ′+

1IC（L－d2sin θ+R）（L－d2cos θ）］∫t0Fndt（28）

vEy=vi+［1m+1IC（L－d2cos θ）2－

1IC（L－d2sin θ+R）（L－d2cos θ）μ′］∫t0Fndt（29）

定义两个中间量λ1和λ2：

λ1=L－d2sin θ+R" λ2=L－d2cos θ

对式（29）进行积分，可得到永久变形δr：

δr=∫T0vEydt=∫T0vidt+φ1∫T0∫t0Fndt（30）

φ1=IC+mλ22－μ′mλ1λ2mIC

同理，由式（28）可得到滑移长度Ls：

Ls=∫T0vExdt=φ2∫T0∫t0Fndt（31）

φ2=mλ1λ2+μ′（IC－mλ21）mIC

联立式（30）和式（31），可得：

Ls=φ（δr－viT）（32）

φ=φ2φ1=mλ1λ2+μ′（IC－mλ21）IC+mλ22－μ′mλ1λ2（33）

式中，φ定义为比例因子。

结合图3，分析式（32）可得以下关系：① δr≤0，vi≤0且T≥0；② δr－viT≥0。证明如下：因为|vEy|≤|vi|，那么|∫T0vEydt|≤|viT|，即|δr|=|∫T0vEydt|≤|viT|，所以δr－viT≥0。

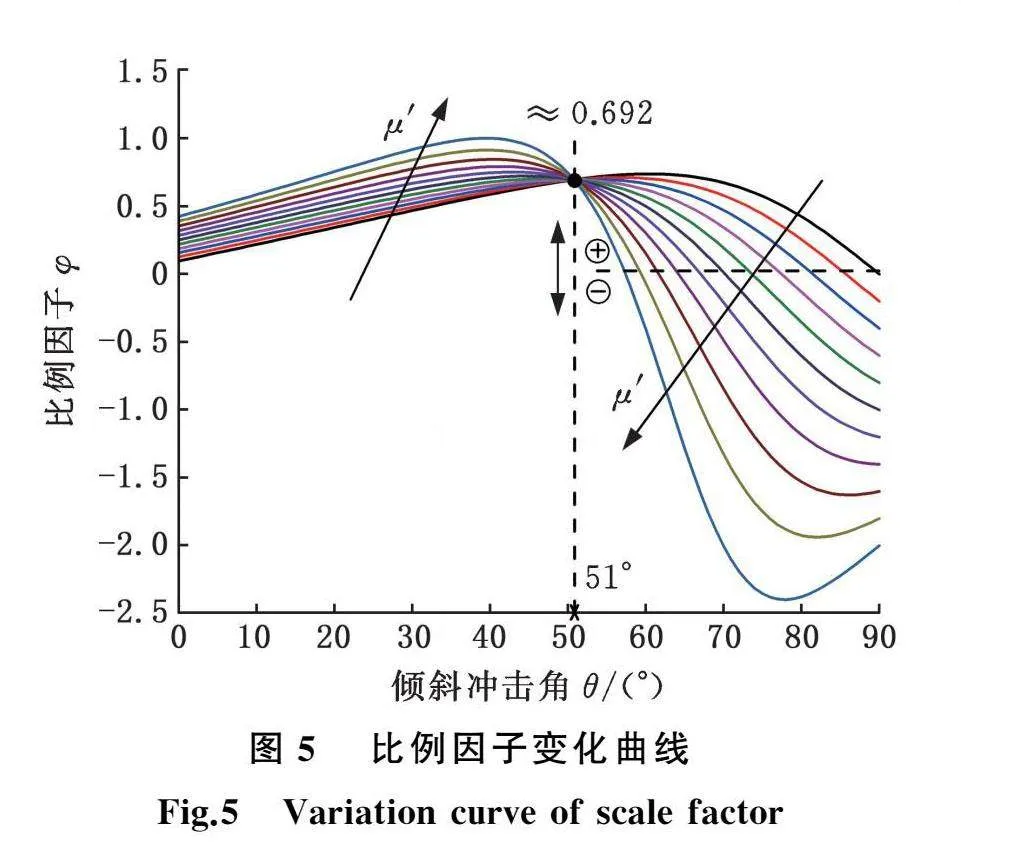
由式（32）和式（33）可知：比例因子φ将滑移长度、永久变形和冲击持时联系起来，其正负实际上决定了滑移的方向；当杆件B的几何参数确定后，比例因子φ是一个关于倾斜冲击角θ和摩擦因数μ′的函数。图5所示为不同摩擦因数μ′∈［0，1］下φ随θ的变化规律。

分析图5可知：①对于任意摩擦因数的比例因子变化曲线，均存在正负号变化的现象，这是因为随着倾斜冲击角的增大，摩擦力矩越来越大于法向力矩，越容易产生黏着摩擦；②不同摩擦因数下的比例因子变化曲线存在一个交点，即当θ=51°时，φ≈0.692；③当0≤θ≤51°时，随着摩擦因数的增大，倾斜冲击角对应的比例因子越大，且曲线形状呈现上凸趋势；而当51°lt;θ≤90°时，随着摩擦因数的增大，对应的比例因子曲线形状越来越呈现V形，即先增大后减小；④随着摩擦因数的增大，比例因子出现符号变化所对应的倾斜冲击角越小。

3 试验数据

本文第一作者等的前期工作［8］中：采用3D高速摄像机跟踪捕获了冲击对象上各标识点的运动学数据，完成了倾斜冲击角θ为45°、坠落高度H为0.05～0.85 m（间隔0.05 m）的倾斜接触冲击试验。其中，杆件B的长度L和直径d分别为150 mm、18 mm。使用数字图像处理方法分析所采集的视频图像，得到冲击对象在接触冲击前后的运动试验数据，如图6～图8所示。

由图6可知：对于接触点E的切向速度，其接触冲击前理论值均为零，冲击前试验值的最大绝对误差与平均绝对误差分别为0.1012 m/s、0.067 m/s；接触冲击后理论值随坠落高度的增加而增大，试验值尽管存在一定的波动，

但变化基本趋势相似，当H≤0.2 m时，其误差值较大，这是因为当坠落高度较小时，杆件B除接触点之外的部分甚至还感觉不到冲击，即受到应力分布速度的影响，而当0.2 m＜H≤0.85 m时，其最大相对误差与平均误差分别为16.84%、10.27%。

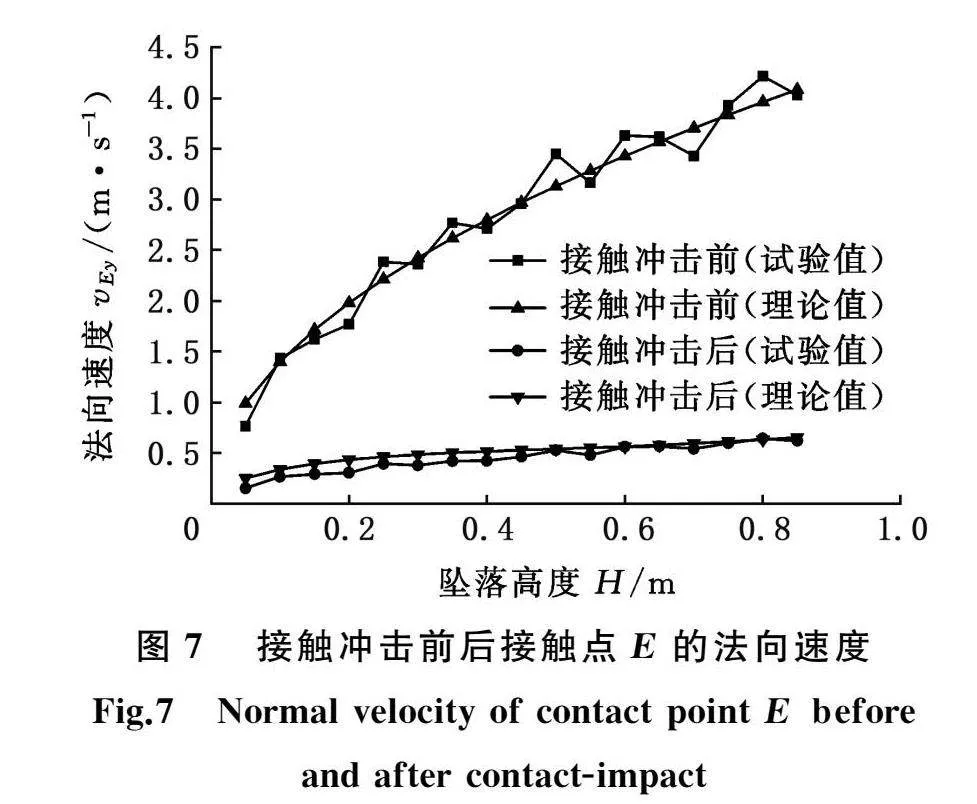
由图7可知：对于接触点E的法向速度，其接触冲击前后的理论值均随坠落高度的增加而增大，相应试验值尽管存在一定的波动，但变化基本趋势相似；接触冲击前试验值的最大相对误差与平均相对误差分别为12.04%、6.23%；受到应力分布速度的影响，与接触点E切向速度冲击后的情况类似，当H≤0.2 m时，接触冲击后的误差值较大；而当0.2 m＜H≤0.85 m时，接触冲击后试验值的最大相对误差与平均相对误差分别为19.36%、10.82%。

由图8可知：对于杆件的角速度ω，其接触冲击前理论值均为零，冲击前试验值的最大绝对误差与平均绝对误差分别为0.2034 rad/s、0.093 rad/s；接触冲击后理论值（负号代表方向）随坠落高度的增加而增大，试验值尽管存在一定的波动，但变化基本趋势相似，其最大相对误差与平均误差分别为20.44%、8.39%。

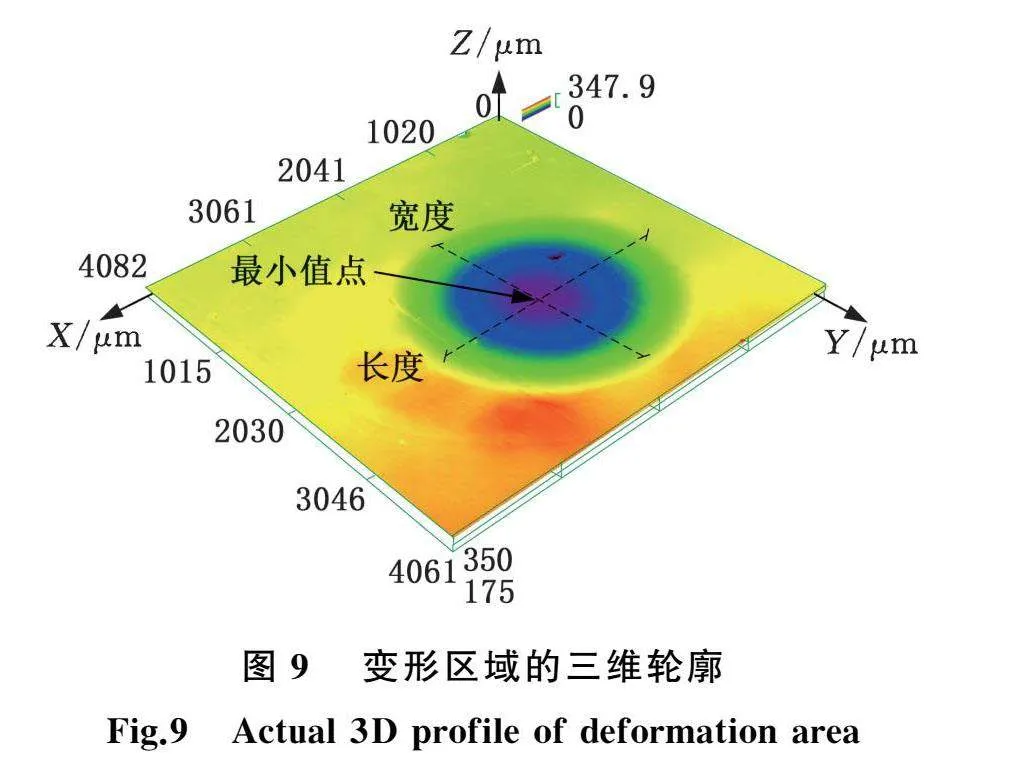
每次接触冲击事件完成后，用记号笔对变形区轮廓进行框选标记，再采用CLSM测量得到变形区域的三维轮廓。由于表面粗糙度（Ra≤1.6 μm）的影响可以忽略，故轮廓区域内距离表面的最小值点即最大深度对应永久变形，而变形区域内最小值点所在的轮廓最大长度与宽度之差对应滑移长度。图9所示为初始坠落高度0.30 m、倾斜冲击角45°下变形区域的三维轮廓，所测得的永久变形δr为347.9 μm，滑移长度Ls为42.8 μm。

4 结果与分析

杆件B和平面S的材料属性参数如下：杆件B的密度7850 kg/m3，弹性模量206 GPa，泊松比0.28，屈服强度248 MPa；平面S的密度7737 kg/m3，弹性模量48 GPa，泊松比0.285，屈服强度66 MPa。本文重点关注永久变形和滑移长度这两个表征参数，分别对基于Brake压陷模型直接积分法和基于广义动量定理建立的解析求解法进行数值求解，并与试验结果进行对比分析。

4.1 摩擦因数

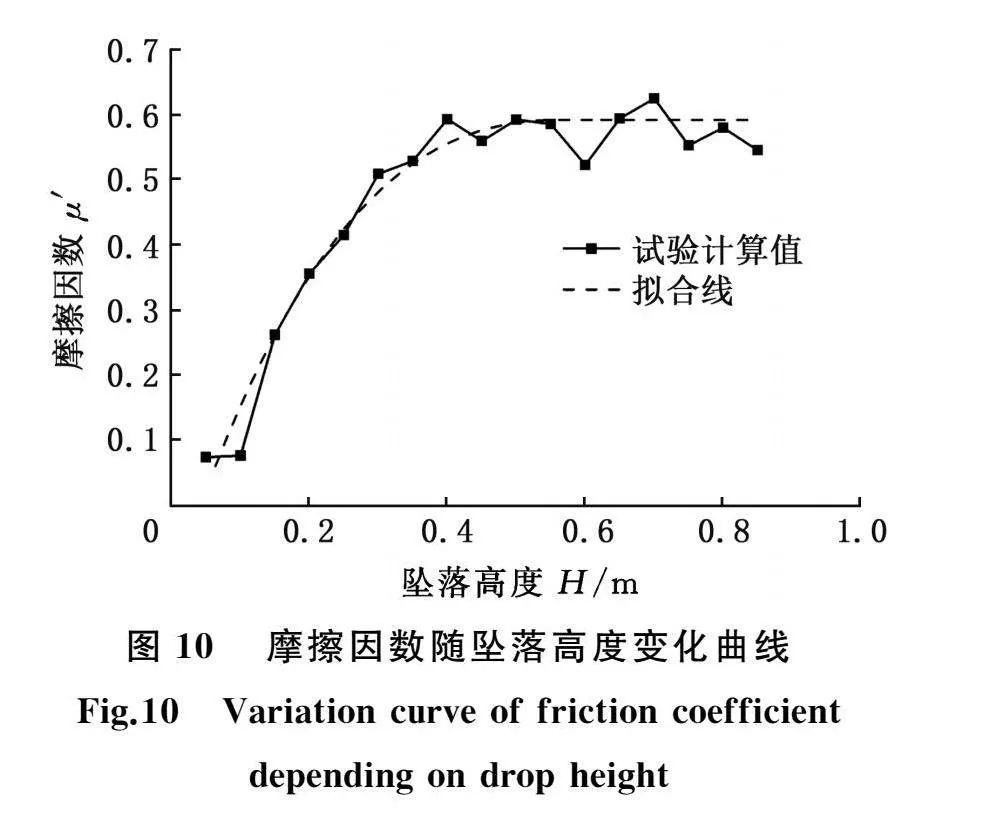
将运动试验数据代入式（27）计算可以得到不同坠落高度H下的摩擦因数μ′，如图10所示。由图10可知：摩擦因数随坠落高度（即初始冲击速度）的增加而增大，且当坠落高度大于0.45 m时，摩擦因数趋于波动稳定，见图10中虚线拟合线。

4.2 比例因子

当倾斜冲击角θ=45°时，由式（33）计算得到不同坠落高度H下的比例因子φ，如图11所示。由图11可知：随坠落高度的增加，比例因子先增大、后趋于波动稳定，见图11中虚线拟合线；结合图10分析可知：不同坠落高度下比例因子与摩擦因数的变化规律呈相似变化趋势，存在正相关关系。

4.3 恢复系数

恢复系数e能够表征接触冲击物体的变形恢复能力。图12所示为Brake压陷模型的恢复系数计算值与试验值的对比分析。由图12中试验拟合线（虚线）可知：随坠落高度的增加，恢复系数先减小、后趋于稳定，即当Hgt;0.45 m时，e≈0.1531；与试验值相比，Brake模型的恢复系数计算值整体上偏大，但变化趋势相一致，且当Hgt;0.65 m时，e≈0.1601，其平均相对误差为3.88%，而当H≤0.65 m时，Brake模型计算值偏差较大，其平均相对误差为19.65%。分析原因如下：由于巴氏合金材料本身具有良好的镶嵌性与减摩性［24］，因而在低速冲击下，其弹性域衰减可能会更快；再者巴氏合金力学性能受制造工艺的影响，那么应变硬化［25］是一个重要的修正量因素。由此，该模型弹塑性阶段的表达式需要进一步分析与验证。

4.4 永久变形

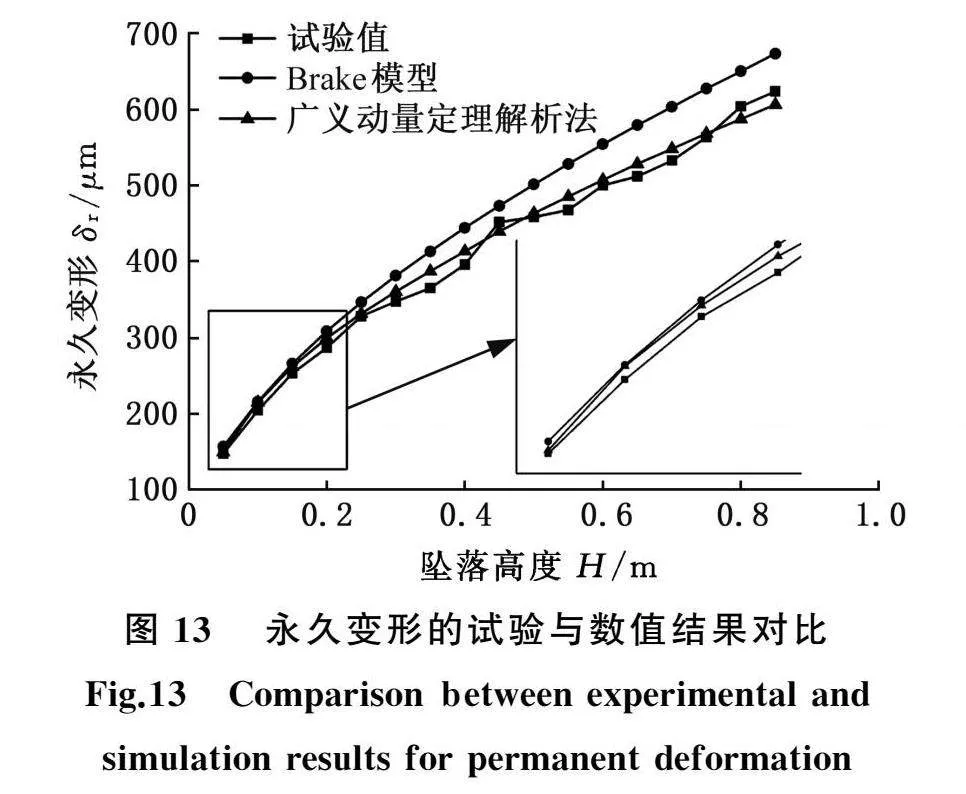
图13所示为永久变形δr的试验值与Brake模型数值解、广义动量定理解析解的对比分析。由图13可知：Brake模型、广义动量定理解析法与试验值的变化趋势一致，即δr的试验值随坠落高度H的增加呈现递增的变化趋势；对于Brake模型，其最大相对误差为13.24%，平均相对误差为9.21%；而广义动量定理解析法的最大相对误差为6.07%，平均相对误差为3.02%，可见，广义动量定理解析法与试验值吻合较好且与Brake模型相比，其计算结果更准确。分析原因如下：Brake模型中忽略了振动响应对运动参数及接触变形的影响［8，14］，随着坠落高度的增加，振动响应越明显，而广义动量解析法与冲击前后质心C的运动参数（实验数据）相关。

4.5 滑移长度

图14所示为滑移长度Ls的试验值与Brake模型数值解、广义动量定理解析解的对比分析。由图14可知：随坠落高度H的增加，Ls的试验值整体呈递增趋势；对于Brake模型，其滑移长度数值解均大于试验值，约为试验值的1.9倍，且曲线变化率逐渐减小，但明显大于试验曲线变化率；而广义动量定理解析法求解的滑移长度变化曲线，则在试验曲线附近存在一定的波动现象。广义动量定理解析法求解的滑移长度变化曲线，其平均绝对误差为10.5 μm，平均相对误差为19.88%，但相比Brake模型，其计算结果与试验值更接近。

分析原因如下：①结合图6～图8的分析，对于采用Brake压陷模型直接积分数学方程求解方法，其接触冲击后运动参数（如接触点E的切向/法向速度、杆件的角速度）与试验值的平均绝对误差约10%，这是造成求解滑移长度误差很大的重要因素，在振动响应的影响研究方面已有发现［8，14］；②采用广义动量定理所建立的求解方法，虽然在求解永久变形上，因为变量参数取自实验数据而呈现较好的表现，但对于求解滑移长度，相较于共识的允许误差仍较大，极可能的原因在于杆件接触点处自身的变形影响（即碰撞两物体均发生变形［18，26］），该变形虽对永久变形的求解有一定影响，但相当于系统误差（接触点E的y向速度），而对于滑移长度，则存在摩擦学要素的影响，例如摩擦类型、摩擦因数、应变硬化、硬度、摩擦蠕变等［27-28］，这都将导致接触力变化的强非线性特征；③研究中的每个实验数据是在不同坠落高度下的独立冲击事件，尽管是同一个冲击平面S，但其接触点局部性质并不完全相同，那么杆件B的运动参数误差会对解析计算产生一定的影响；④由于巴氏合金的力学/摩擦学特性［29-30］，黏着摩擦很可能造成波动。因此，在后续研究中还需进行更多实验设计，如碰撞两物体材料互换、其他弹塑性材料等，修正与完善模型，以提高模型的精度与普适性。

5 结论

（1）本文以杆件B和平面S组成的杆件平面系统（弹塑性材料）为研究对象，首先建立了系统运动学模型，根据Brake压陷模型建立了瞬时接触力和接触变形的计算式，系统地描述了弹塑性接触冲击过程，永久变形和滑移长度可由直接积分数学方程求解；其次结合冲击对象在接触冲击前后的运动试验数据，基于广义动量定理对冲击持时、永久变形和滑移长度的内在关系进行了解析分析，建立了永久变形和滑移长度的解析求解方法；最后通过运动参数、永久变形与滑移长度的试验数据，对比分析了Brake模型数值解和广义动量定理解析解。

（2）提出了比例因子φ的概念，从而将滑移长度、永久变形和冲击持时联系起来，其正负号决定了滑移的方向；φ是一个关于倾斜冲击角θ和摩擦因数μ′的函数，对于任意摩擦因数的比例因子变化曲线，均存在正负号变化的现象，换言之，随着倾斜冲击角的增大，摩擦力矩越来越大于法向力矩，越容易产生黏着摩擦。

（3）对于倾斜冲击角θ=45°、不同坠落高度H下的接触冲击事件：对于摩擦因数μ′和比例因子φ，两变量的变化规律呈现相似变化趋势，存在正相关关系；对于恢复系数e，Brake模型的恢复系数计算值整体上偏大，但变化趋势与试验值相一致；对于永久变形δr，Brake模型、广义动量定理解析法与试验值的变化趋势一致，广义动量定理解析法与试验值吻合较好且与Brake模型相比，其计算结果更准确；对于滑移长度Ls，Brake模型的滑移长度数值解均大于试验值（约1.9倍），而广义动量定理解析法则是在试验曲线附近存在一定的波动现象，相比Brake模型，其计算结果与试验值更接近。

未来的研究方向如下：一方面对Brake模型弹塑性阶段的表达式进行进一步的分析、修正与完善，以优化模型对恢复系数的表征效果；另一方面，考虑相关影响因素，如黏着摩擦判断，优化广义动量定理解析法，提高对滑移长度的求解精度，并且在后续研究中，需要进行更多的实验设计（如碰撞两物体材料互换等），以提高模型的普适性。

参考文献：

［1］ ZHENG Qi， GUO Yacong， WEI Yanpeng， et al. Loosening of Steel Threaded Connection Subjected to Axial Compressive Impact Loading［J］. International Journal of Impact Engineering， 2020， 144：103662.

［2］ PENG Q， YE Xiaoxia， WU H， et al. Effect of Plasticity on Dynamic Impact in a Journal-bearing System：a Planar Case［J］. Mechanism and Machine Theory， 2020， 154：104034.

［3］ JIA Chao， FANG Zongde， YAO Ligang， et al. Tooth Flank Modification to Reduce Transmission Error and Mesh-in Impact Force in Consideration of Contact Ratio for Helical Gears［J］. Proceedings of the Institution of Mechanical Engineers， Part C：Journal of Mechanical Engineering Science， 2021， 235（19）：4475-4493.

［4］ 武和全， 旷世杰， 胡林. 老年乘员在自动驾驶车辆中的碰撞响应研究［J］. 机械工程学报， 2020， 56（12）：144-154.

WU Hequan， KUANG Shijie， HU Lin. Research on Collision Response of Elderly Occupant in Autonomous Vehicles［J］. Journal of Mechanical Engineering， 2020， 56（12）：144-154.

［5］ 刘茜， 程靖， 梁建勋. 混合碰撞建模方法及其试验验证［J］. 机械工程学报， 2022， 58（1）：116-123.

LIU Qian， CHENG Jing， LIANG Jianxun. Novel Hybrid Method for Contact Analysis and Experiment Test［J］. Journal of Mechanical Engineering， 2022， 58（1）：116-123.

［6］ AHMADIZADEH M， SHAFEI A M， FOOLADI M. Dynamic Analysis of Multiple Inclined and Frictional Impact-contacts in Multi-branch Robotic Systems［J］. Applied Mathematical Modelling，2021，91：24-42.

［7］ HERTZ H. Ueber die Berührung Fester Elastischer Krper［J］. Journal Für die Reine und Angewandte Mathematik，1882，92：156-171.

［8］ 王尧， 孟文俊， 项丹， 等. 基于数字图像处理方法的弹塑性倾斜接触冲击动力学试验与数值分析［J］. 机械工程学报， 2019， 55（1）：81-90.

WANG Yao， MENG Wenjun， XIANG Dan， et al. Experimental and Numerical Analysis of the Elasto-plastic Oblique Contact-impact Dynamics Using Digital Image Processing Method［J］. Journal of Mechanical Engineering， 2019， 55（1）：81-90.

［9］ GHAEDNIA H， BRAKE M R W， BERRYHILL M， et al. Strain Hardening from Elastic-perfectly Plastic to Perfectly Elastic Flattening Single Asperity Contact［J］. Journal of Tribology， 2019， 141（3）：031402.

［10］ WANG Hui， YIN Xiaochun， HAO H， et al. The Correlation of Theoretical Contact Models for Normal Elastic-plastic Impacts［J］. International Journal of Solids and Structures，2020，182/183：15-33.

［11］ DONG Xiaoyun， YIN Xiaochun， DENG Qingming， et al. Local Contact Behavior between Elastic and Elastic-plastic Bodies［J］. International Journal of Solids and Structures， 2018， 150：22-39.

［12］ 王尧， 张铁锋， 施韦伊， 等. 杆件与倾斜平面弹塑性接触冲击动力学建模与分析［J］. 中国机械工程， 2020， 31（11）：1261-1269.

WANG Yao， ZHANG Tiefeng， SHI Weiyi， et al. Dynamics Modelling and Analysis of Elasto-plastic Contact-impact of a Rod-like Structure with a Oblique Flat Surface［J］. China Mechanical Engineering， 2020， 31（11）：1261-1269.

［13］ 王尧， 付庄. 杆件平面系统弹塑性接触冲击特性研究进展［J］. 现代制造工程， 2019（9）：141-149.

WANG Yao， FU Zhuang. Research Review on Elasto-plastic Contact-impact Behavior of Rod-flat System［J］. Modern Manufacturing Engineering， 2019（9）：141-149.

［14］ MENG Wenjun， WANG Yao. Comprehensive Analyses of the Elasto-plastic Oblique Contact-impact with Vibration Response［J］. Proceedings of the Institution of Mechanical Engineers， Part K：Journal of Multi-Body Dynamics， 2019， 233（2）：441-454.

［15］ WANG Yao， FU Zhuang. Analytical Study of Babbitt/Steel Composite Structural Bars in Oblique Contact-impact with a Solid Flat Surface［J］. Mechanical Sciences， 2019， 10（1）：213-228.

［16］ BRAKE M R W. An Analytical Elastic Plastic Contact Model with Strain Hardening and Frictional Effects for Normal and Oblique Impacts［J］. International Journal of Solids and Structures， 2015， 62：104-123.

［17］ JACKSON R L， GREEN I. A Statistical Model of Elasto-plastic Asperity Contact between Rough Surfaces［J］. Tribology International， 2006， 39（9）：906-914.

［18］ GHEADNIA H， CERMIK O， MARGHITU D B. Experimental and Theoretical Analysis of the Elasto-plastic Oblique Impact of a Rod with a Flat［J］. International Journal of Impact Engineering， 2015， 86：307-317.

［19］ SKRINJAR L， SLAVICˇ J， BOLTEAR M. A Review of Continuous Contact-force Models in Multibody Dynamics［J］. International Journal of Mechanical Sciences， 2018， 145：171-187.

［20］ LUNDBERG B， RASTEMO T， HUO J. Effect of Pre-impact Waves in an Elastic Rod on Coefficient of Restitution［J］. International Journal of Impact Engineering， 2021， 151：103816.

［21］ ZHANG Xiang， VU-QUOC L. Modeling the Dependence of the Coefficient of Restitution on the Impact Velocity in Elasto-plastic Collisions［J］. International Journal of Impact Engineering， 2002， 27（3）：317-341.

［22］ WANG Yao， LI Shujun， XIANG Dan， et al. Experimental and Theoretical Analyses of the Contact-impact Behavior of Babbitt ZChSnSb11-6［J］. Proceedings of the Institution of Mechanical Engineers， Part L：Journal of Materials：Design and Applications， 2019， 233（7）：1267-1276.

［23］ BIWA S， STOR＼RAKERS B. An Analysis of Fully Plastic Brinell Indentation［J］. Journal of Mechanics Physics of Solids， 1995， 43（8）：1303-1333.

［24］ 李淑君， 王尧， 项丹， 等. ZChSnSb11-6/20钢复合材料结合界面影响因子研究［J］. 稀有金属材料与工程， 2016， 45（10）：2555-2560."" LI Shujun， WANG Yao， XIANG Dan， et al. Impact Factor of Binding Interface on ZChSnSb11-6/20 Steel Composites［J］. Rare Metal Materials and Engineering， 2016， 45（10）：2555-2560.

［25］ GAO Chenghui， PROUDHON H， LIU Ming. Three-dimensional Finite Element Analysis of Shallow Indentation of Rough Strain-hardening Surface［J］. Friction， 2019， 7（6）：587-602.

［26］ GHAEDNIA H， WANG Xianzhang， SAHA S， et al. A Review of Elastic-plastic Contact Mechanics［J］. Applied Mechanics Reviews， 2017， 69（6）：060804.

［27］ WANG Xianzhang， AN Bowen， XU Yang， et al. The Effect of Resolution on the Deterministic Finite Element Elastic-plastic Rough Surface Contact under Combined Normal and Tangential Loading［J］. Tribology International， 2020， 144：106141.

［28］ SALARI S， BEHESHTI A. Asperity-based Contact and Static Friction with Provision for Creep：a Review［J］. Surfaces and Interfaces， 2021， 24：101144.

［29］ ZAINULABDEEN A A， HASHIM F A， ASSI S H. Mechanical Properties of Tin-based Babbitt Alloy Using the Direct Extrusion Technique［J］. IOP Conference Series：Materials Science and Engineering， 2019， 518（3）：032031.

［30］ NI Yuquan， ZHANG Hui， DONG Guangneng. Tribological Performances of Modified Babbitt Alloy under Different Sliding Modes［J］. Journal of Tribology， 2021， 143（6）：061402.

（编辑 陈 勇）