采油单螺杆泵动态力学特性及疲劳寿命预测研究

摘要：针对常规采油螺杆泵定子橡胶疲劳失效的问题，以油田常用的GLB120-27型单螺杆泵为研究对象，开展了50 ℃油浸工况下定子橡胶材料疲劳试验，获取了橡胶材料的疲劳性能参数，并构建了疲劳寿命预测模型。运用ABAQUS软件对螺杆泵进行动态力学特性有限元分析，基于数值模拟得到应力应变响应结果和定子橡胶材料单轴拉伸试验应力应变拟合表达式，计算了疲劳危险位置点应变能释放率的范围。利用构建的疲劳寿命预测模型对不同过盈量条件下的螺杆泵进行了疲劳寿命预测研究。结果表明，随着过盈量的增加，疲劳寿命呈指数函数下降，通过与某采油厂近5年单螺杆泵平均工作寿命的对比，发现基于裂纹扩展方法预测得到的螺杆泵定子橡胶疲劳寿命可以满足工程预测精度要求。

关键词：螺杆泵；动态力学特性；定子橡胶；疲劳寿命预测

中图分类号：TH145.9

DOI：10.3969/j.issn.1004132X.2024.08.003

开放科学（资源服务）标识码（OSID）：

Study on Dynamic Mechanics Characteristics and Fatigue Life Prediction of

Single PCPs

ZU Haiying SUN Jinshan YE Weidong LI Daqi

College of Mechanical Science and Engineering，Northeast Petroleum University，Daqing，

Heilongjiang，163318

Abstract： Aiming at the rubber fatigue failures of the stator of conventional production PCPs， the fatigue test of stator rubber material under 50 ℃ oil immersion condition was carried out with GLB120-27 type single PCP as the research object， the fatigue performance parameters of rubber material were obtained， and the fatigue life prediction model was established. The dynamic mechanics characteristics of PCPs were analyzed by finite element method with ABAQUS software. Based on the stress-strain response results obtained by numerical simulation and the stress-strain fitting expression of stator rubber materials in uniaxial tensile tests， the range of strain energy release rate at fatigue danger points was calculated. The fatigue life prediction of PCPs under different interference conditions was studied by using the established fatigue life prediction model. The results show that the fatigue life decreases exponentially with the increase of interference. Compared with the average working life of a single PCP in recent 5 years， based on crack propagation method the fatigue life of the stator rubber may meet the requirements of engineering prediction accuracy.

Key words： progressing cavity pump（PCP）; dynamic mechanics characteristic; stator rubber; fatigue life prediction

0 引言

采油螺杆泵是广泛应用于油田机械采油工程中重要的人工举升设备，它由摆线型金属转子与橡胶定子过盈配合组成，定转子共轭啮合运动形成密封腔室，实现对油液的举升。橡胶定子在工作过程中长期处于油、气、液三相混合介质的恶劣环境中，受到高温、高压、油液腐蚀等作用，并伴随发生溶胀、温胀，从而导致疲劳失效，影响了螺杆泵的密封性，进而降低了举升效率［1-2］。为了提高螺杆泵的使用寿命，急需开展其疲劳失效机制的研究。

目前国内外学者采取不同研究方法对橡胶材料进行疲劳寿命预测。黄锴等［3］对硅橡胶复合材料进行了单轴、双轴疲劳拉伸试验，采用有限元分析与Python编程软件相结合的方法提出了橡胶的多轴疲劳寿命算法，并进行了实例验证。殷芳等［4］基于以八面体切应变峰值为损伤参量的寿命预测模型和疲劳裂纹扩展理论，开展了橡胶衬套多轴疲劳寿命预测的研究，结果表明以八面体切应变峰值为损伤参量的寿命预测模型拟合精度相对较高。王文涛等［5］基于橡胶线性疲劳累计损伤原理，建立了张量形式的橡胶悬置预测疲劳寿命表达式，模型预测效果良好。Le GAC等［6］采用理论能量方法，在完全松弛条件下，提出了一种将疲劳寿命与橡胶的交联密度联系起来的新的经验关系式。CHOI等［7］考虑材料各向异性和复杂应力状态，提出了增强聚氯丁橡胶半经验应变寿命（ε-N）疲劳模型，采用6种机器学习模型进行疲劳寿命预测，结果表明深度神经网络模型预测精度最高，平均误差为14.3%。BELKHIRIA等［8］基于应变能密度法，针对典型加载情况，预测橡胶材料疲劳裂纹产生及方位，并建立了裂纹角和主应变的函数关系。目前对动态、流体、固体、热耦合状态下橡胶构件疲劳寿命的研究报道较少。为使研究更符合实际工况，本文对螺杆泵进行热流固耦合条件下的动态力学特性有限元分析，并基于裂纹扩展法对螺杆泵定子橡胶疲劳寿命开展预测研究。

1 定子橡胶疲劳失效机理与寿命预测模型

1.1 定子橡胶疲劳失效机理分析

对螺杆泵的工作原理分析后可知，螺杆泵转子在定子内做行星运动，转子与定子接触面运动形式为滚动加滑动，同时产生的离心力使得转子对定子表面不断循环碾压，导致定子橡胶表面极易出现损伤。由此推断定子橡胶的疲劳磨损裂纹是从表层开始发生的，在接触压力作用下，高压油波迅速侵入裂纹，裂纹壁受到强烈的冲击，进而引起裂纹的深度扩展，导致定子橡胶疲劳失效。定子橡胶内表面的疲劳裂纹萌生如图1所示，实际状况下疲劳失效的形貌如图2所示，这与上述理论分析的结果相吻合。

1.2 定子橡胶疲劳寿命预测模型的建立

基于螺杆泵定子橡胶疲劳失效的机理，本文采用裂纹扩展法对螺杆泵开展疲劳寿命预测研究。选取应变能释放率［9-10］为损伤参量。橡胶在疲劳裂纹扩展过程中，材料的裂纹扩展速率和应变能释放率符合幂函数的关系：

dcdN=BGβ（1）

式中，c为裂纹长度；N为疲劳寿命（疲劳周次）；G为应变能释放率；dc/dN 为裂纹扩展速率；β为疲劳特性参数；B为常数。

RIVLIN等［11］对无切口和带有预制切口的橡胶试件进行拉伸疲劳试验，确定橡胶试件切口扩展应变能释放率表达式为

k（λ）=π/λ（2）

式中，W0为无切口试件的应变能密度；k（λ）为比例常数；λ为伸长比。

将式（2）代入式（1），得到在循环载荷作用下试件的应变能与裂纹扩展率的关系：

dcdN=B（2πλ cW0）β （3）

基于断裂力学理论，橡胶材料内部具有初始微裂纹，微裂纹在疲劳载荷作用下逐渐扩展，直至失效。对式（3）从初始微裂纹到疲劳失效时的裂纹尺寸进行积分，得到疲劳寿命表达式：

N=∫cc0B-1G-βdc=1B（β-1）（2πλW0）β（1cβ-10-1cβ-1）（4）

式中，c0为初始微裂纹尺寸。

材料内部的初始微裂纹尺寸远远小于构件失效时裂纹尺寸，即c0＜＜c，则式（4）可化简为

N=1B（β-1）（2πλW0）β（1cβ-10）（5）

式（5）为橡胶疲劳寿命预测模型，模型参数B取2.73×10-13［12］。采用德墨西亚等加速疲劳试验方法，获得定子橡胶材料的疲劳特性参数β和初始微裂纹尺寸c0［13］。对式（5）取对数，得到对数疲劳寿命的表达式：

lg N=-β（lg（2πλ）+lg W0）+

［-lg B-lg（β-1）-（β-1）lg c0］（6）

由式（6）可得无切口的试件与预制切口尺寸cn（n=0，1，2，…）的试件的对数疲劳寿命之差an：

an=lg N0-lg Nn=（β-1）（lg cn-lg c0）（7）

分析式（7）可知，对数疲劳寿命之差与伸长比无关，an与lg cn成线性关系，通过直线an-lg cn的斜率和截距，推导出β和c0的表达式：

β=an-a1lg cn-lg c1+1（8）

lg c0=a1lg cn-anlg c1a1-an（9）

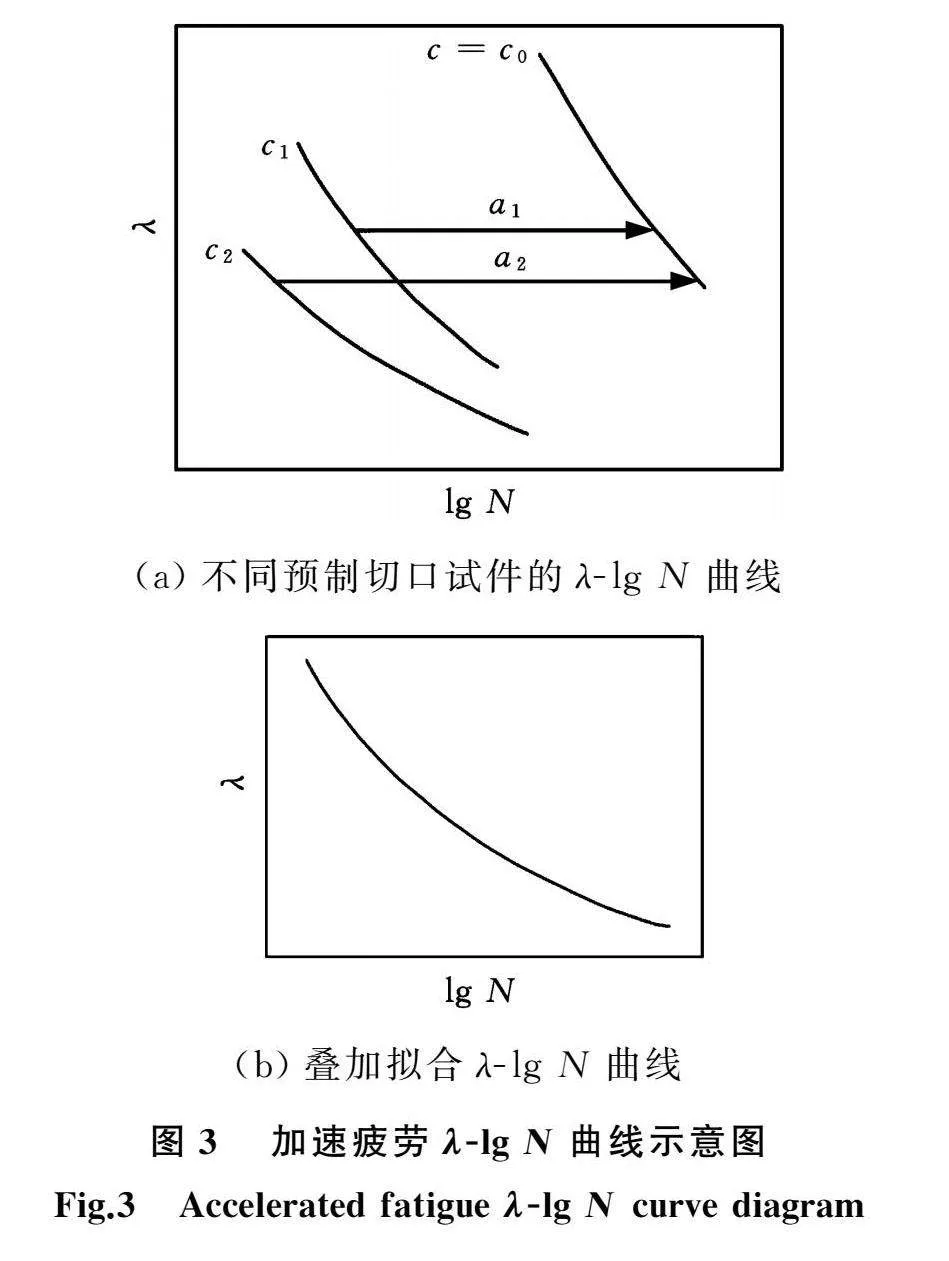
对无切口试件和具有不同预制切口试件进行单轴拉伸疲劳试验，获得不同伸长比下的对数疲劳寿命，依据黏弹行为的叠加原理，确定宽伸长比范围疲劳寿命曲线。试验方案如下：将不同预加切口试件与无切口试件的伸长比对数疲劳寿命曲线叠加，再将曲线平移an，得到宽伸长比范围的疲劳寿命曲线，如图3所示。将平移量和裂纹尺寸代入式（8）、式（9）求解出β和c0。

2 定子橡胶材料疲劳试验

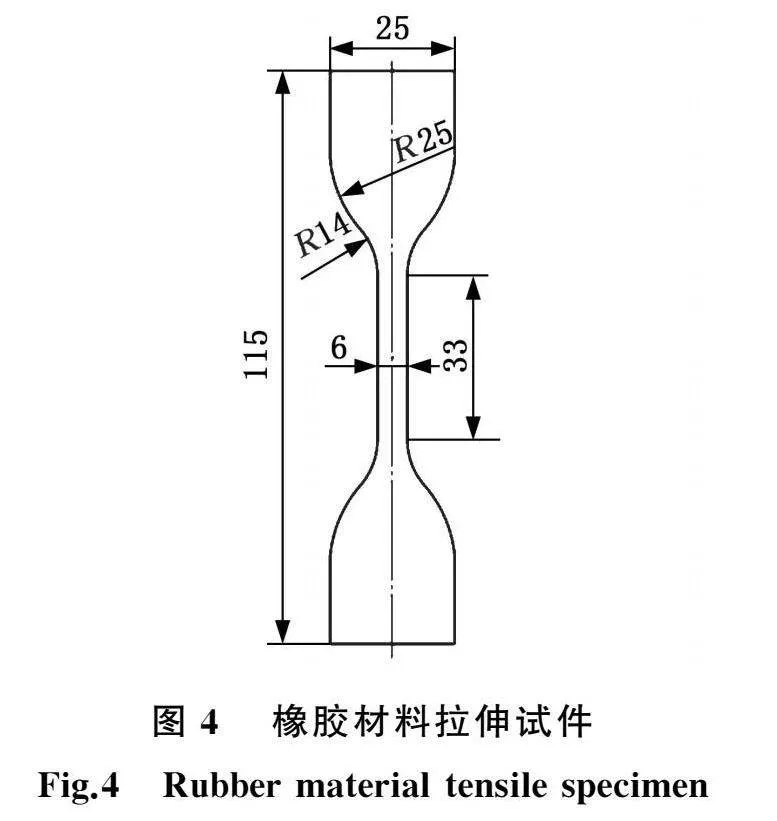
按照国家标准将定子橡胶材料制成标准Ⅰ型哑铃状试件，试件尺寸参数如图4所示。试验前将试件浸泡在50 ℃、0号柴油介质中72 h，利用恒温箱保持温度不变，如图5所示。

2.1 橡胶材料单轴拉伸试验

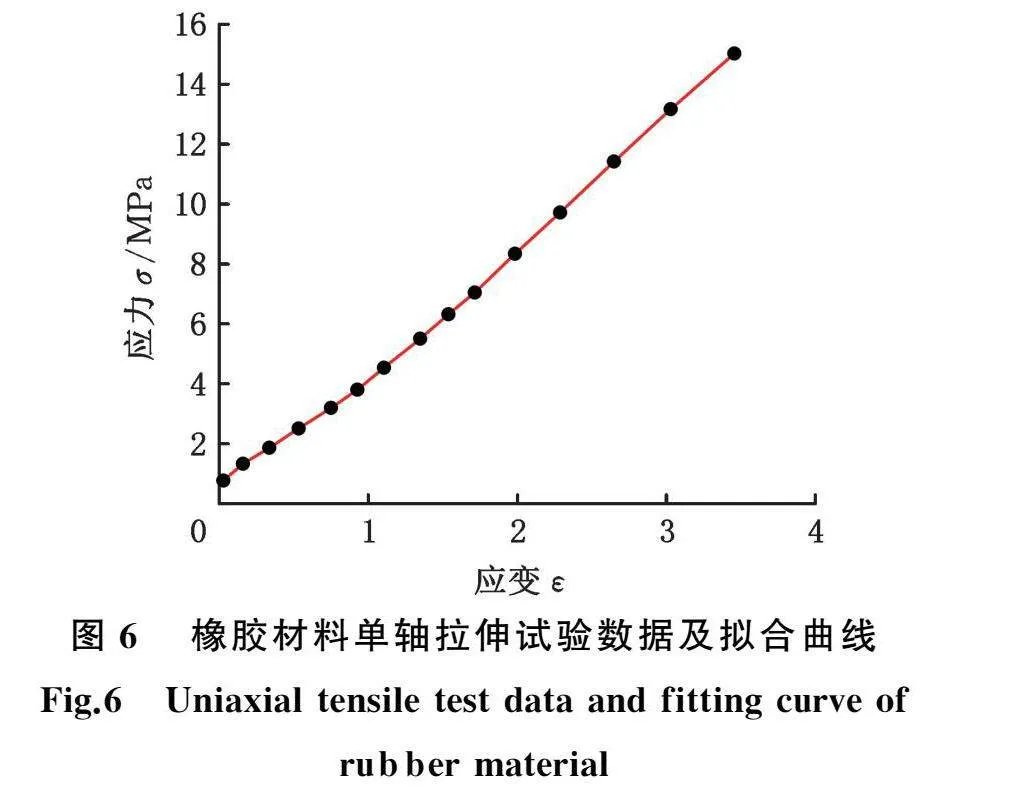
采用岛津公司生产的电子拉力试验机对油浸后的橡胶试件进行单轴拉伸试验，结果取每组试件的平均值，获得50 ℃油浸定子橡胶材料应力应变数据，如图6所示。拟合确定该工况下应力应变关系式：

σ（ε）=-0.124ε3+0.965ε2+2.966ε+0.678（10）

2.2 橡胶材料疲劳试验

将油浸后的橡胶试件分成三组，一组无预制切口试件，两组使用锋利的刀片和专用夹具在试件中心位置分别预制0.2 mm和0.4 mm切口。将橡胶试件自然状态装夹在XP-16型橡胶疲劳试验机上，如图7所示。对三组试件进行单轴拉伸疲劳试验。

橡胶材料进行疲劳试验时，在用力控制的疲劳载荷作用下容易发生蠕变，导致局部应变增加、疲劳寿命降低，因此，本试验采用位移加载方式，按照伸长比计算加载位移。试件原始长度L0为25 mm，拉伸至最大标距长度Lmax，应变ε和试件伸长比λ的计算公式分别为

ε=Lmax/L0-1（11）

λ=Lmax/L0（12）

载荷都从最大位移变化到零，循环加载直至橡胶试件断裂，记录疲劳试验寿命。每个位移下取5个试件进行试验，取其平均值作为结果。

2.3 橡胶材料疲劳试验结果

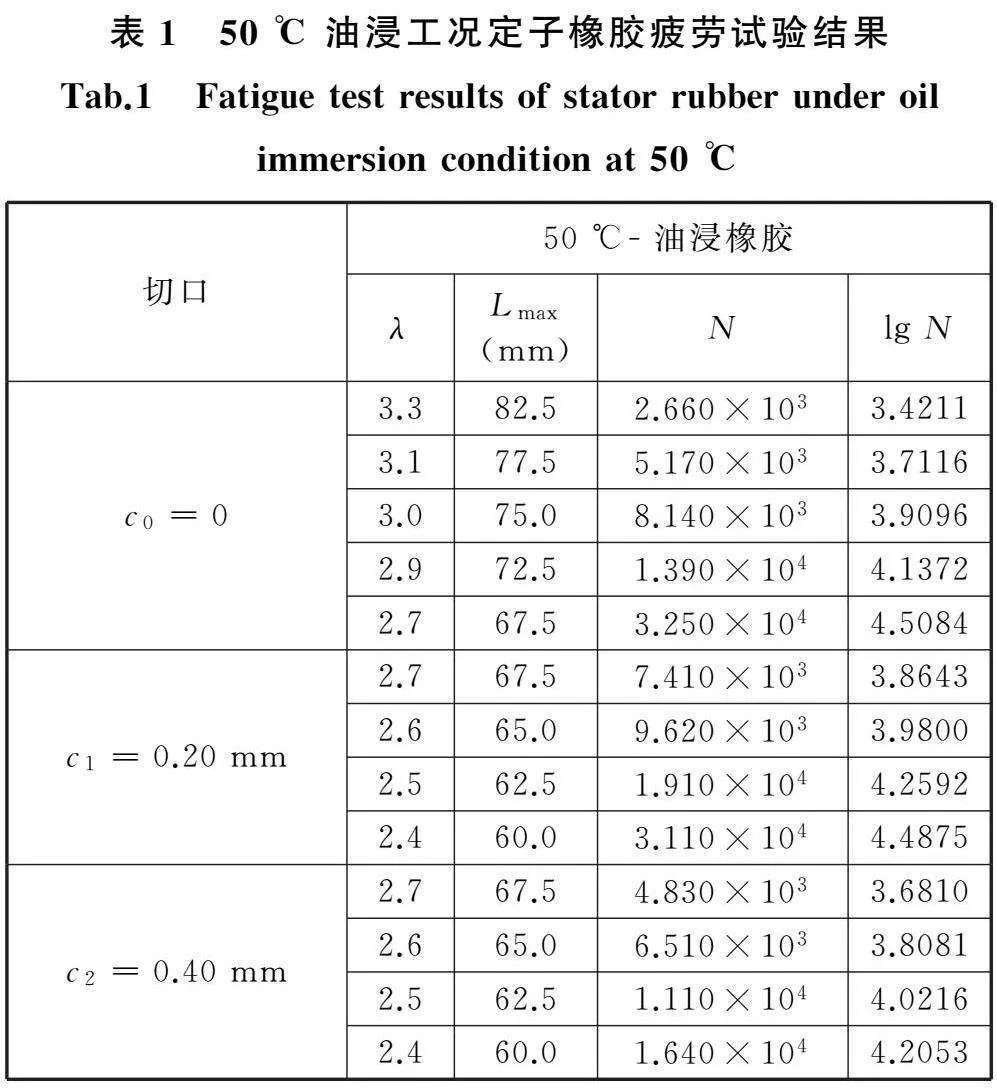
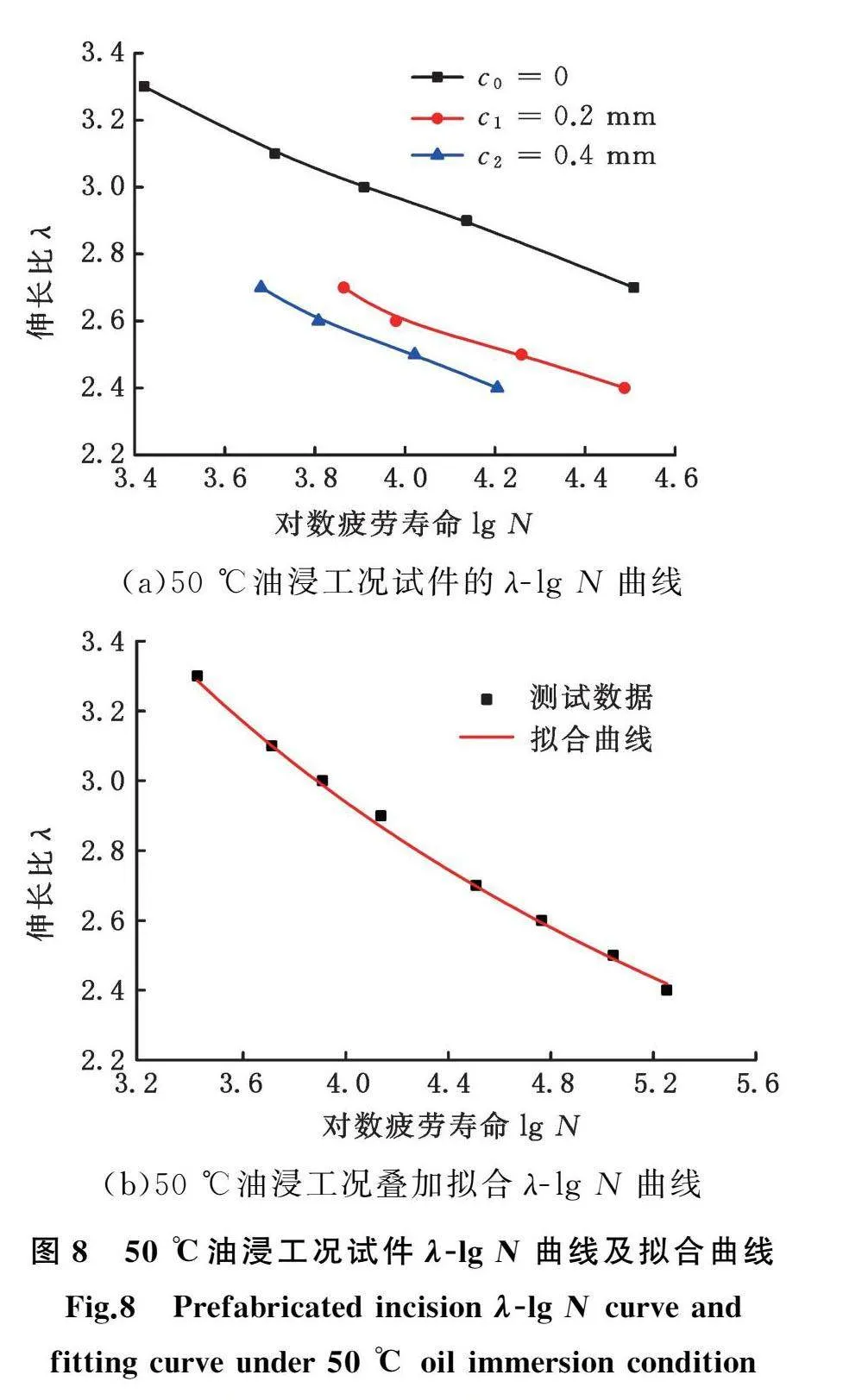
在50 ℃油浸工况下，试件分成无预制切口c0和预制切口c1、c2三组，每组取不同的伸长比进行疲劳试验，试验载荷和寿命结果见表1。将表1中三组试件不同伸长比时平均对数疲劳寿命绘制成三条曲线，如图8a所示。依据黏弹性叠加原理，按照第1节的方法，将预制切口c1、c2疲劳寿命曲线平移a1、a2，与无切口c0疲劳寿命曲线叠加，得到宽应变范围的疲劳寿命曲线，如图8b所示。

将平移量a1、a2和对数疲劳寿命代入式（8）和式（9），计算得到定子橡胶疲劳裂纹扩展特性参数β=2.07和潜在临界损伤等效的裂纹尺寸c0=37 μm。

2.4 试件疲劳断裂位置分析

对比分析试件的疲劳失效断裂位置。工况为无预制切口、50 ℃油浸、伸长比3.0的试件疲劳失效位置如图9a所示。工况为预制切口尺寸0.2 mm、50 ℃油浸、伸长比2.6的试件失效断裂位置如图9b所示。由图9a可知，无预制切口的橡胶试件靠近移动夹持端狭长区域偏上位置发生了疲劳断裂失效，此区域为试件夹持端与狭长部分过渡区域，存在应力集中，且此区域为移动夹持端，位移变化幅度大，因此，无预制切口的试件易在此位置发生疲劳断裂。由图9b可知，有预制切口试件在切口处扩展而发生疲劳断裂，断裂方向与伸长方向有一定夹角。

3 螺杆泵动态力学特性分析

3.1 有限元模型的建立

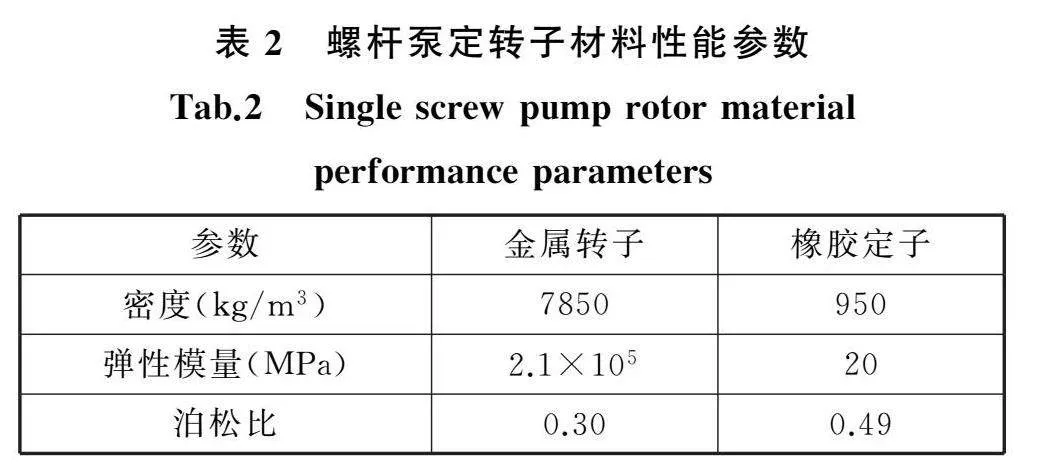
地面驱动螺杆泵，单极举升能力与过盈量密切相关，为满足举升要求，螺杆泵定子与转子间过盈量常用范围为0.2～0.5 mm，最小过盈量一般取0.2 m左右。本文研究对象为油田上广泛使用的GLB120-27型螺杆泵，为分析方便，建立一个导程，过盈量为0.2 mm、0.3 mm、0.4 mm、0.5 mm的四个几何参数模型。将其导入ABAQUS，建立螺杆泵有限元模型，模型采用六面体网格进行划分，如图10所示。在正常工作时，金属转子所产生的变形量远远小于橡胶定子产生的变形量，因此在仿真计算过程中将金属转子设置为刚体。定子橡胶采用Mooney-Rivlin模型，由橡胶材料单轴拉伸试验结果可得模型参数C10为1.840，C01为0.046，定转子材料详细参数见表2。设置模型边界条件如下：设置金属转子横向移动和行星自转，设置定转子的轴向位移以及定子壳体为固定约束，设置整个模型接触属性为通用接触。

3.2 动态力学特性结果分析

在满足精度要求的网格尺寸和较好等效全导程模型计算结果的模型长度的条件下，建立1/4定子导程、网格尺寸为1 mm的GLB120-27型单螺杆泵有限元模型，进行动态力学特性计算。

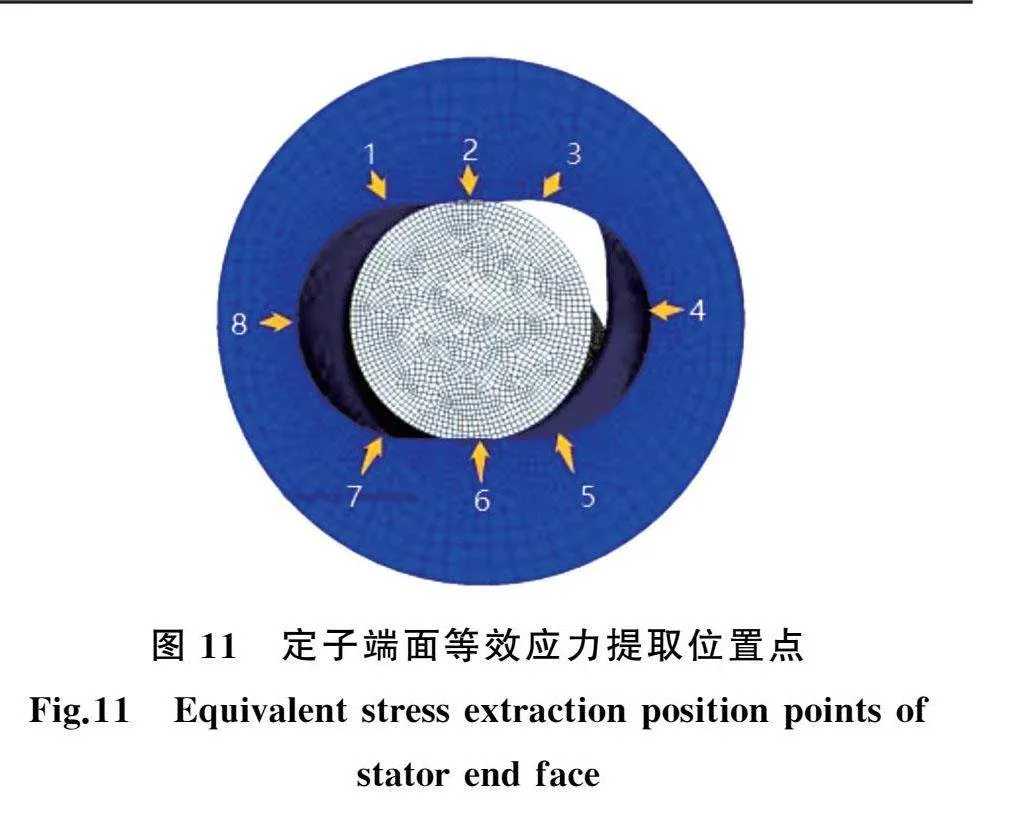
橡胶定子端面由两段圆弧和两段直线段组成长圆形曲线。为了确定橡胶定子最大等效应力位置，沿顺时针方向提取橡胶定子长圆形8个位置点的计算结果进行分析，如图11所示。8个位置点分别记为位置点1～8。

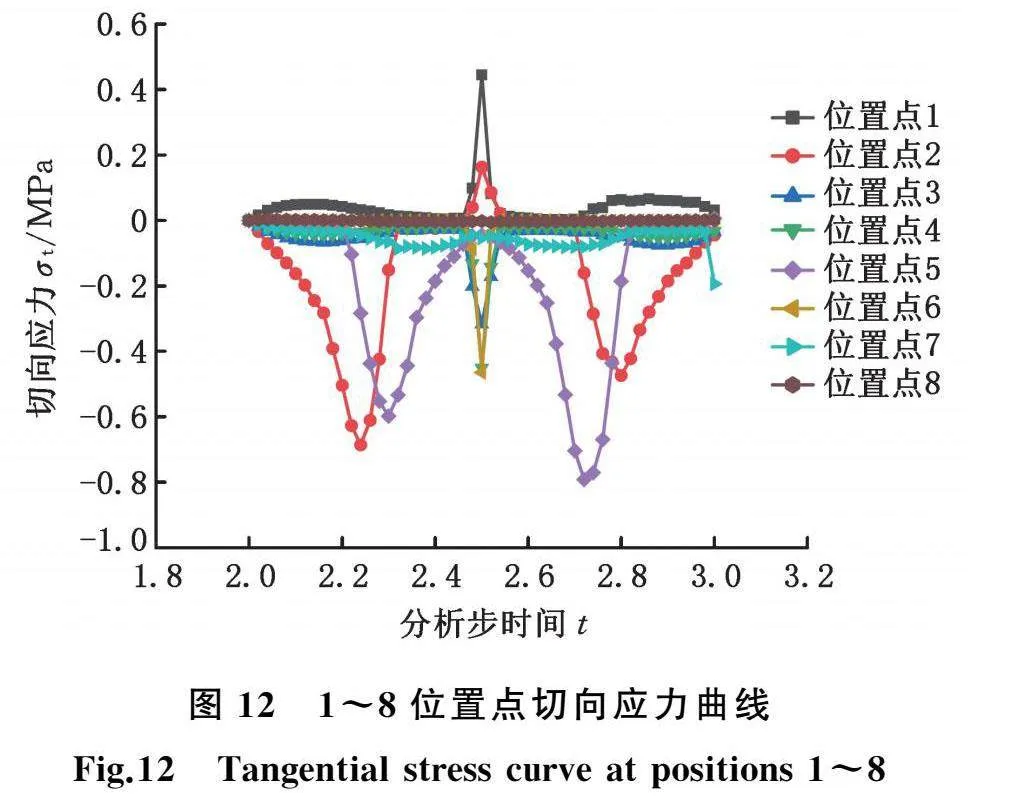
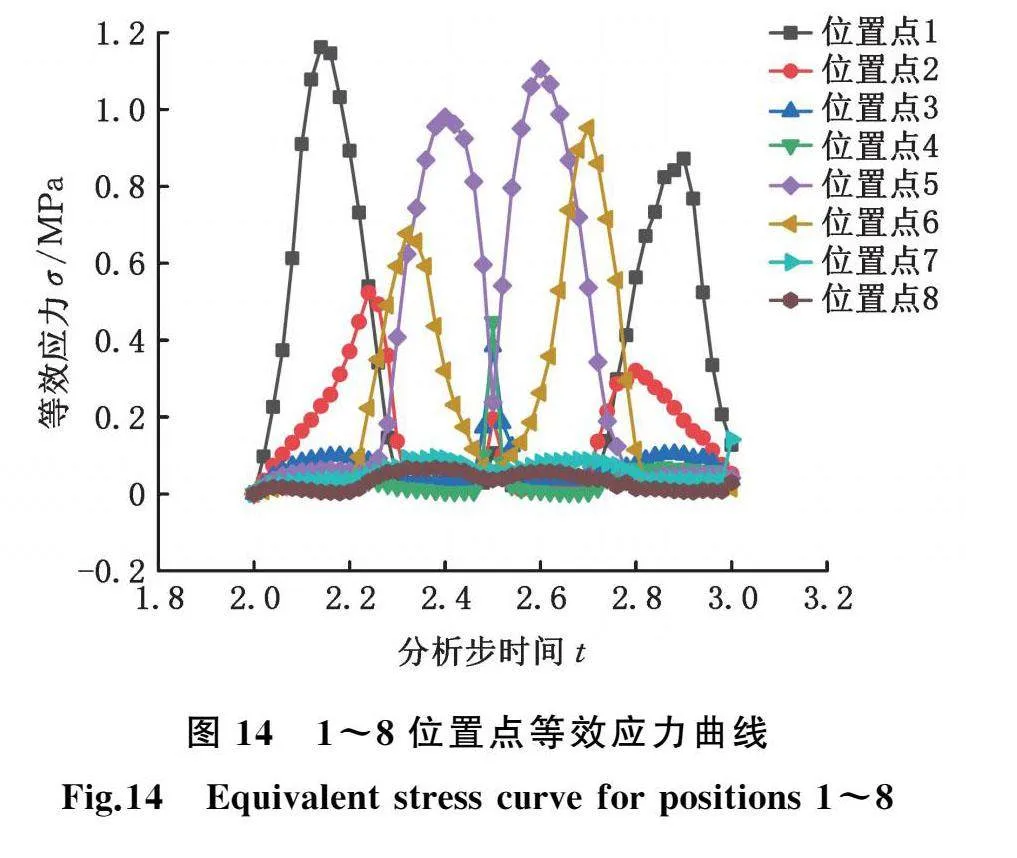
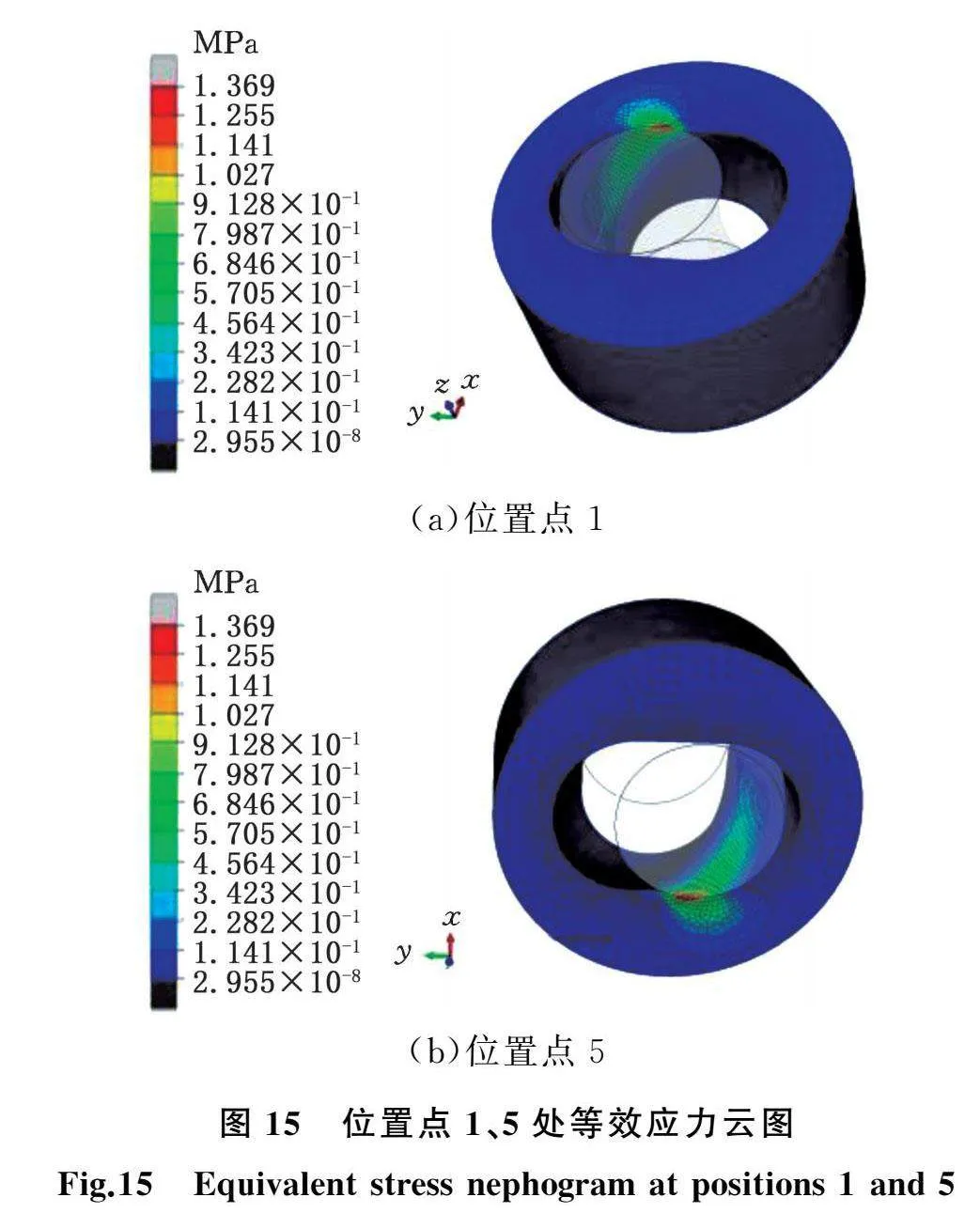
提取8个位置点一个运动周期切向应力、法向应力和等效应力动态力学特性计算结果，并绘制成曲线，如图12～图14所示。可知，切向应力最大峰值位于位置点5处，法向应力和等效应力最大峰值位于位置点1处，次峰值位于位置点5处。由图12可知，位置点1和位置点5处在定子端面长圆形直线段和圆弧段过渡且更靠近直线段位置。列出位置点1和位置点5等效应力云图，如图15所示。

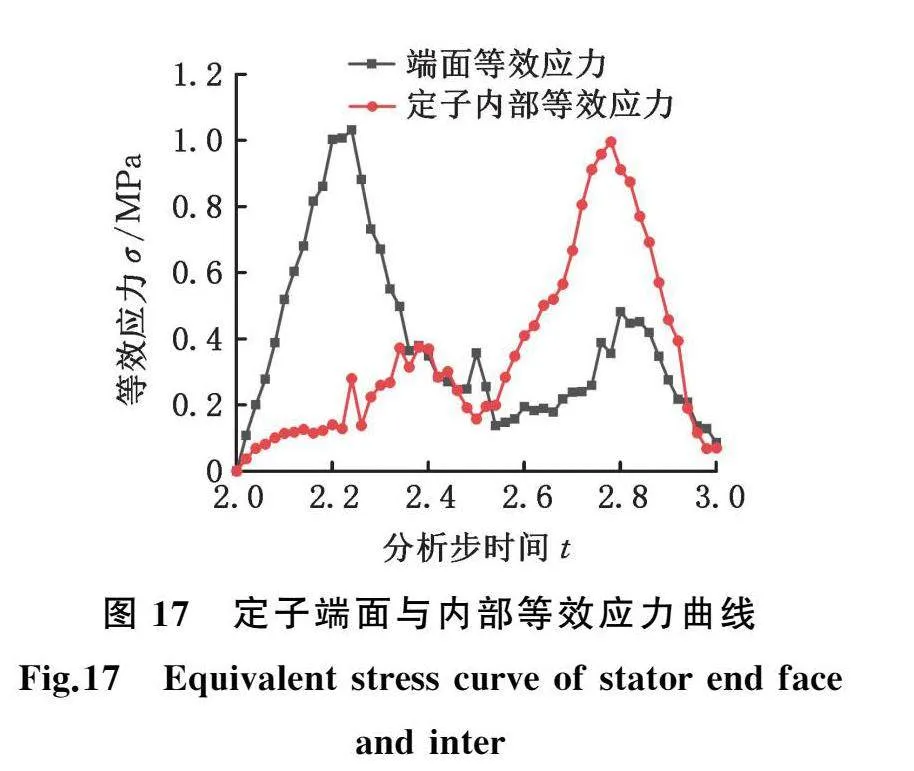
为预测研究螺杆泵疲劳寿命，需确定螺杆泵最易发生疲劳的危险位置。上文已分析了定子端面的力学特性，需进一步研究定子内部力学特性。定子橡胶内部等效应力云图见图16。提取内部最大等效应力位置点一个运动周期的等效应力，与定子端面位置1处等效应力进行对比，如图17所示。

由图17可知，定子内部与端面位置点1处等效应力曲线形状相似，变化趋势一致，两者间仅存在一个相位差。两条曲线最大等效应力峰值基本相同。因此，本文选用定子端面位置点1和位置点5处作为疲劳危险位置点，提取这两个位置的主应力用于后续螺杆泵疲劳寿命的预测计算。同时由动态力学特性仿真分析确定的疲劳危险位置与图1中疲劳裂纹萌生的位置相吻合。

4 定子橡胶疲劳寿命预测与验证

4.1 基于裂纹扩展法的定子橡胶疲劳寿命预测

螺杆泵转子在定子型腔内行星运动且两者之间为过盈配合，工作过程中定子橡胶受到挤压、拉伸、扭转剪切力作用，同时受到高压流体的冲击力作用，受载条件的复杂性使得直接测定应变能释放率变得困难。根据LUO等［14-15］的研究结论，可通过提取橡胶构件疲劳危险位置的主应力计算等效应力，通过等效应力求取等效应变，再由等效应变计算定子橡胶应变能释放率。等效应力计算表达式为

σf=σ21+Aσ22+Cσ23（13）

σ1gt;0" σ1gt;σ2gt;σ3

A=1" σ2gt;0

0σ2≤0

C=1" σ3gt;0

0σ3≤0

式中，σf为等效应力；σ1、σ2、σ3分别为x、y、z方向主应力。

提取不同过盈量螺杆泵数值模拟结果疲劳位置点三项主应力，分别代入式（13）。为模拟螺杆泵实际工况，分析提取施加6 MPa和5 MPa压力高、低压腔室时的应力结果，用来计算最大等效应力和最小等效应力。

通过对定子橡胶材料的单轴拉伸的应力应变拟合表达式式（10）进行积分，获得应变能密度W0，将应变能密度代入应变能释放率表达式式（2），计算出应变能释放率G：

G=2k（λ）cW0=2πc1+ε∫ε0σ（ε）dε（14）

将螺杆泵不同过盈量参数模型计算得到的最大等效应力代入式（10），获得最大等效应变。同理可获得不同过盈量时最小等效应变，再将其代入式（14），计算出最大应变能释放率与最小应变能释放率，两者相减可得到应变能释放率范围。将应变能释放率代入式（5），计算得到50 ℃油浸工况下的预测疲劳寿命，见表3。

4.2 预测疲劳寿命结果分析

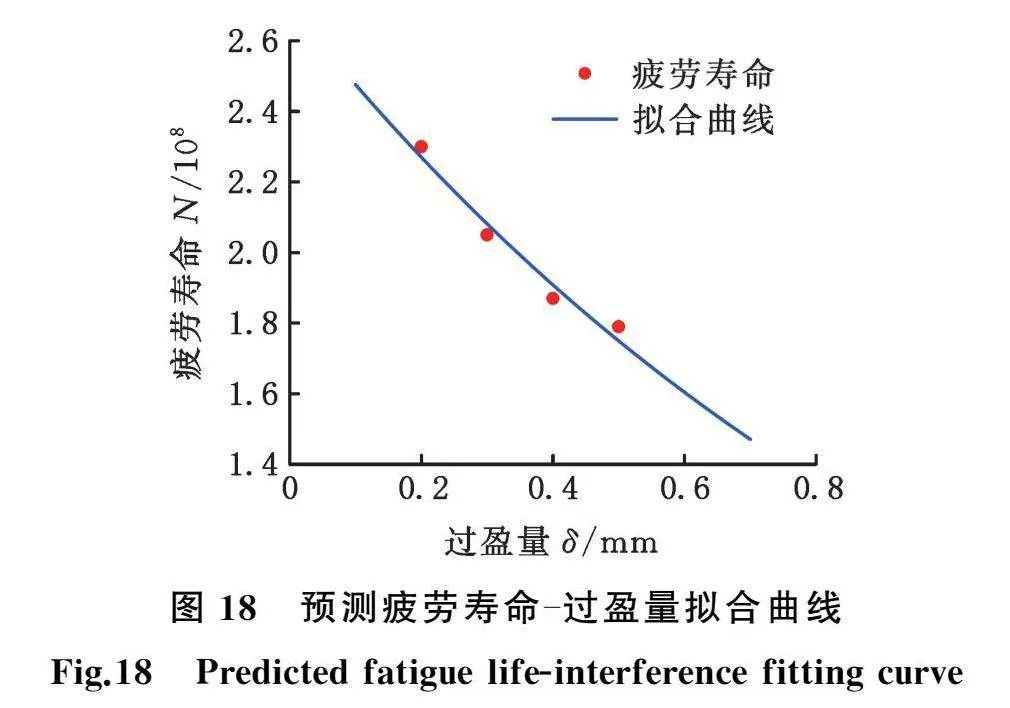
以过盈量为横坐标、预测疲劳寿命为纵坐标绘制散点图，将预测疲劳寿命随过盈量变化进行指数函数拟合，拟合曲线如图18所示。GLB120-27型单螺杆泵偏心距和定子导程一定时，预测疲劳寿命随过盈量变化的拟合表达式为

N=2.6781e-0.844δ×108 （15）

拟合相关系数R2为0.9647，表明拟合精度较高。由表3和图18可知，GLB120-27型单螺杆泵过盈量为0.2～0.5 mm，预测疲劳寿命范围为2.30×108～1.79×108。预测疲劳寿命随过盈量的增加而迅速降低。通过式（15）可以预测其他过盈量的螺杆泵疲劳寿命。

4.3 预测疲劳寿命与实际使用寿命对比验证

为对定子橡胶预测疲劳寿命结果进行验证，将预测疲劳寿命次数结果换算成以天为单位的结果。实际工况下螺杆泵转速约在60～150 r/min范围，一般取100 r/min。按照此转速，采用下式将表3中预测寿命的单位转化为天数：

T=0.6N3600×24（16）

实际生产过程中，螺杆泵采油通常采用过盈量为0.3 mm，因此，将过盈量为0.3 mm时预测的计算结果与某采油厂该型号螺杆泵近5年平均实际使用工作寿命进行对比分析，结果见表4。可以看出预测的疲劳寿命与实际寿命比值为2.31，位于实际寿命2.5倍分散线内，符合橡胶构件疲劳寿命预测的要求。由表4发现，预测寿命比实际寿命偏大，出现这种现象的可能原因如下：采油螺杆泵工作环境为原油、水、天然气等多相介质混合的恶劣条件，预测疲劳寿命时难以模拟螺杆泵实际工作工况。另外，石油中含有砂粒等杂质，定子橡胶易发生磨损，且定子橡胶工作过程有烷、烃、二氧化碳等气体在高压作用下溶入到定子橡胶中，降低了橡胶力学性能。因此，预测寿命与实际寿命产生了一定差距。

5 结论

（1）螺杆泵疲劳失效的机理是定子橡胶表面在循环应力作用下萌生裂纹并不断扩展。本文建立了以应变能释放率为损伤参量的定子橡胶疲劳寿命预测模型。基于德墨西亚等加速疲劳试验方法推导了确定定子橡胶材料的疲劳特性参数和初始微裂纹尺寸表达式。

（2）通过对定子橡胶在50℃油浸条件下的单向拉伸与疲劳实验，拟合出其应力应变关系式，获得了材料大伸长比范围内疲劳寿命曲线，确定了疲劳寿命预测模型的特性参数。

（3）对螺杆泵进行动态力学特性分析，对比了定子端面长圆形8个位置点的周期应力，确定了疲劳危险位置处在直线段和圆弧段过渡且更靠近直线段的位置处。

（4）基于裂纹扩展方法预测了螺杆泵定子橡胶疲劳寿命，结果表明，随着过盈量的增加，疲劳寿命呈指数函数下降。预测寿命与实际使用寿命比值为2.31，预测精度满足工程要求，为螺杆泵疲劳寿命的研究提供了参考。

参考文献：

［1］ 赵艳芳. 螺杆泵故障诊断及预防措施［J］. 化学工程与装备， 2021（7）：182-183.

ZHAO Yanfang. Fault Diagnosis and Preventive Measures of Screw Pump［J］. Chemical Engineering amp; Equipment， 2021（7）：182-183.

［2］ 杨斌. 螺杆泵定子橡胶性能的影响因素分析［J］. 设备管理与维修， 2018（14）：75-76.

YANG Bin. Analysis of Influencing Factors on Rubber Properties of Screw Pump Stator［J］. Plant Maintenance Engineering， 2018（14）：75-76.

［3］ 黄锴， 杨海波， 田明， 等. 硅橡胶复合材料的多轴疲劳寿命计算及优化设计［J］. 合成橡胶工业， 2022， 45（2）：85-90.

HUANG Kai， YANG Haibo， TIAN Ming， et al. Multiaxial Fatigue Life Calculation and Optimal Design of Silicone Rubber Composites［J］. China Synthetic Rubber Industry， 2022， 45（2）：85-90.

［4］ 殷芳， 范让林， 冯程程， 等. 橡胶衬套多轴载荷疲劳寿命预测［J］. 机械强度， 2020， 42（3）：700-707.

YIN Fang， FAN Ranglin， FENG Chengcheng， et al. Prediction of Multiaxial Load Fatigue Life for Rubber Bushing［J］. Journal of Mechanical Strength， 2020， 42（3）：700-707.

［5］ 王文涛， 上官文斌， 段小成， 等. 基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究［J］. 机械工程学报， 2012， 48（10）：56-65.

WANG Wentao， SHANGGUAN Wenbin， DUAN Xiaocheng， et al. Study on Prediction of Fatigue Life of Rubber Mount Based on Linear Cumulative Fatigue Damage Theory［J］. Journal of Mechanical Engineering， 2012， 48（10）：56-65.

［6］ Le GAC P Y， ALBOUY P A， FAYOLLE B， et al. Relationship between Macromolecular Network and Fatigue Properties of Unfilled Polychloroprene Rubber［J］. Polymer Degradation and Stability， 2021， 192：109669.

［7］ CHOI J， QUAGLIATO L， LEE S， et al. Multiaxial Fatigue Life Prediction of Polychloroprene Rubber （CR） Reinforced with Tungsten Nano-particles Based on Semi-empirical and Machine Learning Models［J］. International Journal of Fatigue， 2021， 145：106136.

［8］ BELKHIRIA S， HAMDI A， FATHALLAH R. Cracking Energy Density for Rubber Materials：Computation and Implementation in Multiaxial Fatigue Design［J］. Polymer Engineering amp; Science， 2020， 60（9）：2190-2203.

［9］ 詹江正， 霍佳波， 石世杰. 基于ABAQUS和FE-SAFE的振动疲劳仿真［J］. 桂林航天工业学院学报， 2018， 23（1）：23-29.

ZHAN Jiangzheng， HUO Jiabo， SHI Shijie. Simulation of Vibration Fatigue Based on ABAQUS and FE-SAFE［J］. Journal of Guilin University of Aerospace Technology， 2018， 23（1）：23-29.

［10］ 唐杨. 汽车荷载作用下V形钢桥墩的疲劳分析［J］. 特种结构， 2018， 35（5）：57-62.

TANG Yang. Fatigue Analysis of V-shaped Steel Pier under Vehicle Load［J］. Special Structures， 2018， 35（5）：57-62.

［11］ RIVLIN R S， THOMAS A G. Rupture of Rubber. I. Characteristic Energy for Tearing［J］. Journal of Polymer Science， 1953， 10（3）：291-318.

［12］ 刘兵. 某型飞机作动器密封件密封性能分析及疲劳寿命预测［D］. 哈尔滨：哈尔滨工业大学， 2011.

LIU Bing. The Sealing Performance Analysis and Fatigue Life Predication of the Seals of Certain Type Aircraft Actuator［D］. Harbin：Harbin Institute of Technology， 2011.

［13］ 深堀美英， 徐广源. 弹性体疲劳寿命的预测——由断裂力学引出S-N曲线的理论解析及其应用［J］. 橡胶译丛， 1986， 13（4）：67-76.

SHEN Kumeiying， XU Guangyuan. Prediction of Fatigue Life of Elastomer—Theoretical Analysis and Application of S-N Curve Derived from Fracture Mechanics［J］. World Rubber Industry， 1986， 13（4）：67-76.

［14］ LUO R K， WU W X， COOK P W， et al. An Approach to Evaluate the Service Life of Rubber Springs Used in Rail Vehicle Suspensions［J］. Proceedings of the Institution of Mechanical Engineers， Part F：Journal of Rail and Rapid Transit， 2004， 218（2）：173-177.

［15］ LUO R K， WU W X. Fatigue Failure Analysis of Anti-vibration Rubber Spring［J］. Engineering Failure Analysis， 2006， 13（1）：110-116.

（编辑 陈 勇）