反比例函数与几何综合问题探析

【摘要】反比例函数是中学数学的重要内容之一，与几何知识的综合问题具有较高的难度和综合性．本文通过具体实例进行详细分析，旨在帮助学生更好地理解和掌握反比例函数与几何综合问题的解题思路，提高学生的数学综合素养和解决问题的能力．

【关键词】反比例函数；初中数学；解题方法

反比例函数与几何综合问题不仅考查学生对反比例函数和几何知识的掌握程度，还考查学生的综合分析能力、逻辑思维能力和创新能力．因此，深入研究反比例函数与几何综合问题具有重要的现实意义．

1 已知反比例函数图象和三角形面积求解参数

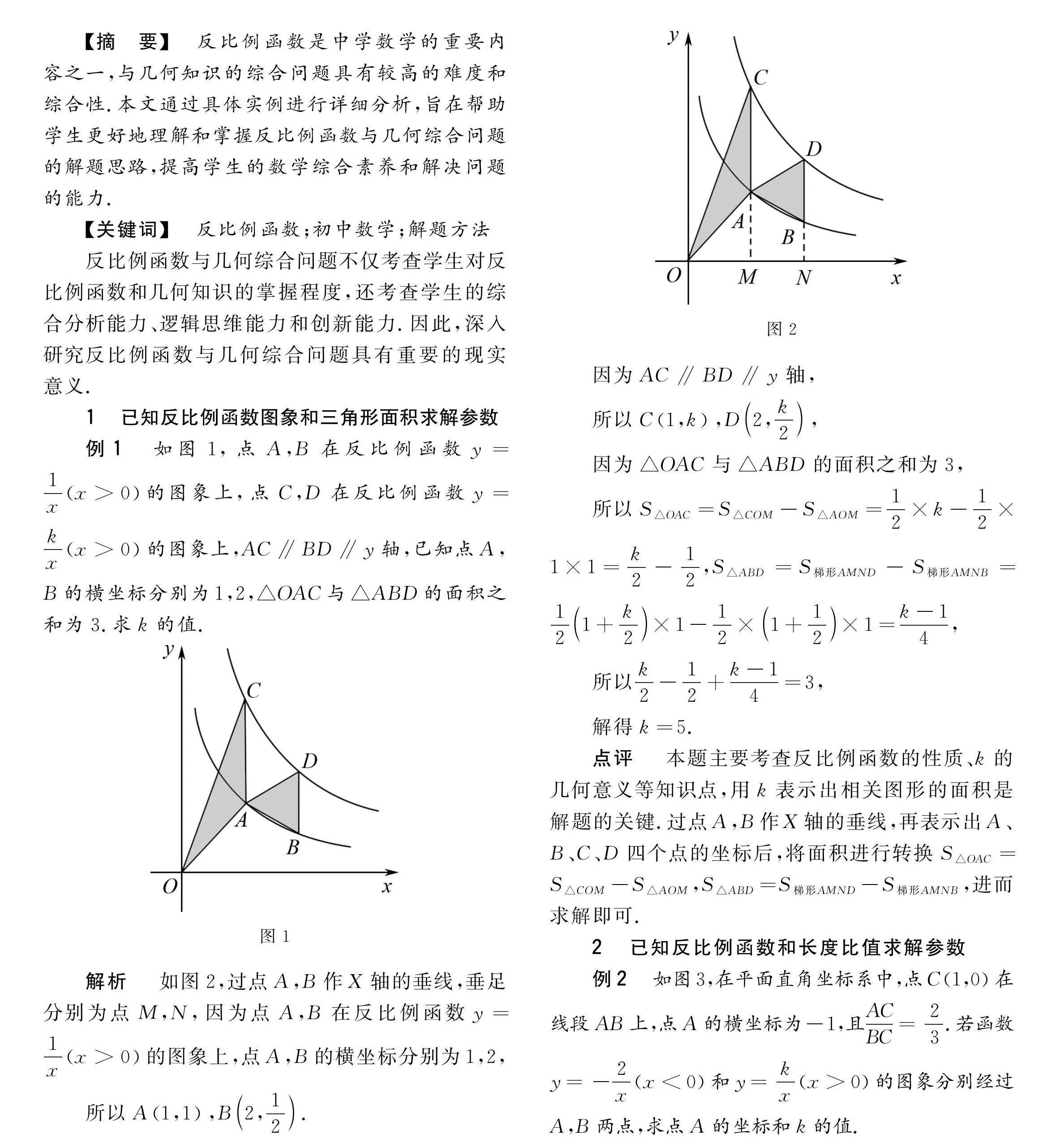
例1 如图1，点A，B在反比例函数y=1xx＞0的图象上，点C，D在反比例函数y=kxx＞0的图象上，AC∥BD∥y轴，已知点A，B的横坐标分别为1，2，△OAC与△ABD的面积之和为3．求k的值．

解析 如图2，过点A，B作X轴的垂线，垂足分别为点M，N，因为点A，B在反比例函数y=1xx＞0的图象上，点A，B的横坐标分别为1，2，

所以A1，1，B2，12.

因为AC∥BD∥y轴，

所以C1，k，D2，k2，

因为△OAC与△ABD的面积之和为3，

所以S△OAC=S△COM－S△AOM=12×k－12×1×1=k2－12，S△ABD=S梯形AMND－S梯形AMNB=121+k2×1－12×1+12×1=k－14，

所以k2－12+k－14=3，

解得k=5．

点评 本题主要考查反比例函数的性质、k的几何意义等知识点，用k表示出相关图形的面积是解题的关键．过点A，B作X轴的

垂线，再表示出A、B、C、D四个点的坐标后，将面积进行转换S△OAC=S△COM－S△AOM，S△ABD=S梯形AMND－S梯形AMNB，进而求解即可．

2 已知反比例函数和长度比值求解参数

例2 如图3，在平面直角坐标系中，点C1，0在线段AB上，点A的横坐标为－1，且ACBC=23．若函数y=－2xx<0和y=kxx>0的图象分别经过A，B两点，求点A的坐标和k的值．

解析 如图4，分别过点A、B作AD⊥x轴于点D，BE⊥x轴于点E，则AD∥BE，

所以△ADC∽△BEC，

所以ADBE=CDCE=ACBC=23，

因为点A的横坐标为－1，

反比例函数y=－2x（x<0）经过点A，

所以点A的坐标为－1，2，

又因为C1，0，

所以AD=2，CD=2，

所以2BE=2CE=23，

得BE=3，CE=3，

所以点B的坐标为4，－3，

因为y=kx（x>0）的图象经过点B，

所以k=4×－3=－12．

点评 本题考查反比例函数图象上点的坐标特征、相似三角形的判定与性质、坐标与图形等知识点，熟练掌握相似三角形的性质是解答的关键．本题中，分别过点A、B作AD⊥x轴于点D，BE⊥x轴于点E，则AD∥BE，根据反比例函数图象的性质即可求出点A的坐标，根据相似三角形的判定与性质以及坐标与图形求得CE和BE，即可求出点B的坐标．

3 已知反比例函数求解三角形面积

例3 如图5，在平面直角坐标系中，已知函数y1=6xx>0，y2=－2xx<0， 点 M 在y 轴的正半轴上，点N在x轴上，过点 M作y 轴的垂线分别交函数y1，y2的图象于A，B两点，连接AN，BN，则△ABN的面积为 ．

解析 过点A，B作x轴的垂线，垂足分别为点G，H，如图6，

因为AB⊥y轴，

所以AB∥x轴，

因为BH⊥x轴，AG⊥x轴，

所以BH∥AG，

所以四边形BHGA，四边形BHOM，四边形MOGA都为矩形，

因为y1=6xx>0，y2=－2xx<0，

所以S矩形BHOM=2，S矩形MOGA=6，

所以S矩形BHGA=S矩形BHOM+S矩形MOGA=8，

所以S△ABN=12S矩形BHGA=4．

点评 本题考查了反比例函数k值的几何意义及反比例函数与几何的综合问题．过点A，B作x轴的垂线，垂足分别为点G，H，易得四边形BHGA，四边形BHOM，四边形MOGA都为矩形，则S矩形BHOM=2，S矩形MOGA=6，进而得出S矩形BHGA=S矩形BHOM+S矩形MOGA=8，最后根据S△ABN=12S矩形BHGA即可得出问题答案．

4 结语

反比例函数与几何综合问题是中学数学中的重要内容，具有较高的难度和综合性．通过对反比例函数的基本性质、反比例函数与几何综合问题的类型、解题方法和策略的分析，可以看出解决这类问题需要学生熟练掌握反比例函数和几何知识，灵活运用各种解题方法和策略．在教学中，教师应注重培养学生的综合分析能力、逻辑思维能力和创新能力，引导学生多思考、多总结，提高学生解决反比例函数与几何综合问题的能力．

参考文献：

[1]刘晓娟.反比例函数的几何综合问题专练[J].现代中学生（初中版），2022（20）：37-38.

[2]段卫华.反比例函数+几何问题例说[J].数理天地（初中版），2019（07）：18-19.

[3]黄晴，贾建宁.巧用平面几何知识来解反比例函数的综合问题[J].数学之友，2023，37（02）：62-63.