大断面隧道爆破施工方案及振动衰减规律

摘 要：本文以实际隧道爆破工程为背景，研究大断面隧道III级围岩上台阶钻爆法及爆破振动衰减规律。在工程实践中，通过现场大量爆破振动监测数据收集，利用非线性回归分析建立大断面隧道III级围岩爆破振动衰减模型，并且得到上台阶爆破施工方案，为后期类似工程提供参考。

关键词：大断面；隧道工程；方案；非线性分析

中图分类号：U 45" 文献标志码：A

国内外的学者很早前就对爆破地震波进行研究，并得出规律。孔宪军[1]分析了矿山爆破振动效应，在现场将矿下监测数据与地表监测数据进行对比，矿下的主频率高但是持续时间短，地表主频率低但是持续时间长。谢烽[2]研究了与爆破点不同距离爆破振动衰减规律。翟渊博[3]认为萨道夫斯基经验公式预测对距离爆破点较远的监测点预测振动速度较慢，不适合预测距离爆破点较远的监测点。贾虎[4]整理分析现场爆破振动数据时发现，距离爆破点较远的爆破振动速度峰值在很大程度上跟最大单段药量密切相关，背向自由面的振动最大，侧向次之，面向自由面最小。朱传统等 [5]对爆破作业时产生的振动进行多次监测，通过监测数据分析得出爆破施工时产生的振动峰值速度表达式。卢文波等[6]基于传统爆破振动预测经验公式，通过现场爆破施工产生的振动进行数据监测，采用回归分析方法得出爆破振动预测公式。

1 工程概况

以分离式布置隧道为背景，其长度为3595m。隧址区属于剥蚀丘陵地貌，区域内山体宽大，连绵起伏，自然斜坡多为20°～40°，峰顶海拔一般多为250～350m。区域内多为林地，地势稍低处多为旱地或水田，种植水稻等农作物。丘陵间冲沟比较发育，多呈条带状分布，局部路段分布比较密集。岩性以粉砂岩、泥质粉砂岩、泥岩、页岩为主。

2 爆破方案设计

2.1 打孔设备及要求

采用气腿式凿岩机YT28直径40mm进行钻孔作业，该型号凿岩机因其高效率、耐用性及适用于硬岩和复杂地质条件而广泛应用于隧道工程领域，并在III级围岩条件下能够高效地完成钻孔工作，同时可以保证孔径满足装药需求和爆破效果设计。

准备阶段：标定炮孔位置，安装并调整气腿式凿岩机YT28，保证其稳定可靠。

钻孔阶段：操作人员按照预定孔位进行钻孔，在过程中需要检查孔深和垂直度，并做好记录。

2.2 循环进尺

循环进尺选择需要考虑岩石硬度和完整性、设备性能、爆破效果、安全要求和施工效率等因素：根据工程经验，循环进尺为3m，即在每次钻孔并进行爆破后，预计可以安全有效地破碎和移除深3m的岩石。

2.3 炮孔深度

炮孔利用率为85%，则孔深L=3/0.85=3.52m，取3.6m。

2.4 掏槽孔

掏槽孔深度设定：根据实际情况及岩石特性，确定掏槽孔的深度为4.0m。

掏槽孔布置位置：掏槽孔位于隧道断面的中下部，这样可以充分利用掏槽孔破裂岩石的力量，引导主爆破区域的岩石向中心部位垮落，有利于提高爆破效率和减少围岩应力集中。

掏槽孔形状与排布方式：采用复式楔形掏槽布局，每对掏槽孔呈对称或近似对称排列，形成一个由浅至深、角度逐渐增加的扇形结构。将掏槽孔与工作面之间的夹角θ设定为60°～80°，便于逐步扩大破碎面积并有效控制爆破能量分布。

钻孔精度要求：为了保证复式楔形掏槽达到预期的良好爆破效果，要尽量缩小钻孔偏差，包括保证炮孔轴线的直线性、垂直度以及相对位置的准确性等，使每个炮孔都能按照预定的角度和深度准确无误地钻设。

2.5 周边孔

周边孔位置设定：周边孔应布置在距离开挖断面边缘0.1～0.2m的位置。当有效破碎围岩时，这样设计可以保证隧道轮廓线附近的岩石结构稳定，减少超挖和欠挖现象。

周边孔倾斜方向与深度控制：要求周边孔的孔底向隧道轮廓线方向倾斜。这样有助于将爆破能量引导至开挖轮廓线上，提高爆破效果并保证断面形状符合设计要求。当遇到坚硬岩体时，为了提高破碎硬岩的能力，周边孔的孔底可以达到或稍微超出轮廓线位置，从而更有效地破碎这些难以处理的岩层。

2.6 单孔装药量

在爆破工程中，需要根据岩体的物理力学性质、裂缝发育状况以及周围环境条件等因素精确计算各炮孔的装药量。单孔装药量的计算过程如公式（1）所示。

Q=r×n×L （1）

式中：n为炮孔装药系数；L为各炮孔孔深，m；r为每米的炸药量，采用2号乳化岩石炸药，r=1.0kg/m。装药量参数见表1。

2.7 爆破网路设计

在爆破方案的起爆系统设计中，采用数码电子雷管起爆技术，保证精准控制，保障安全性。

数码电子雷管应用：在每个炮孔内装入一发数码电子雷管，与传统雷管相比，数码电子雷管具有更高的精度、更高的安全性和更灵活的编程能力。

多段微差起爆设计：设置各段间延时时间为50ms，采用多段微差起爆方式，有效控制爆破能量释放顺序和速度，减少爆破振动对围岩及周围环境的影响。

起爆顺序安排：首先，起爆掏槽孔，利用楔形掏槽的方式引导主爆破区域岩石破碎垮落。其次，起爆辅助孔，进一步扩大破碎范围。再次，起爆底板孔，稳定底部岩石结构，防止下部围岩塌落。最后，同时起爆周边孔，按照“由内向外”的顺序，使爆破效应从中心向四周逐步扩散，对隧道断面进行良好控制。

3 基于非线性回归分析大断面隧道爆破振动

在大断面隧道爆破施工过程中，高度重视振动监测与控制工作。基于现场实际采集的大断面隧道爆破引起的振动数据，采用非线性回归分析方法进行深入研究和精确计算。随着爆破施工的逐步推进，振动监测点的位置也随之动态调整和优化，设置在二次衬砌到洞口区域之间，以便全面获取各个阶段的振动信息，为后续的爆破方案微调提供准确依据。

目前，在我国的爆破振动预测领域，仍然采用国外专家萨道夫斯基提出的经典振动预测公式。该公式是在大量现场爆破试验及丰富的实践经验基础上提炼总结的，对我国爆破工程实践具有重要的理论意义和实用价值。计算过程如公式（2）所示。

（2）

式中；V为监测点爆破振动速度，cm/s，Q为最大单段药量；R为爆破点到监测点的距离，m；K、α为爆破区域以及附近地形有关的衰减系数。

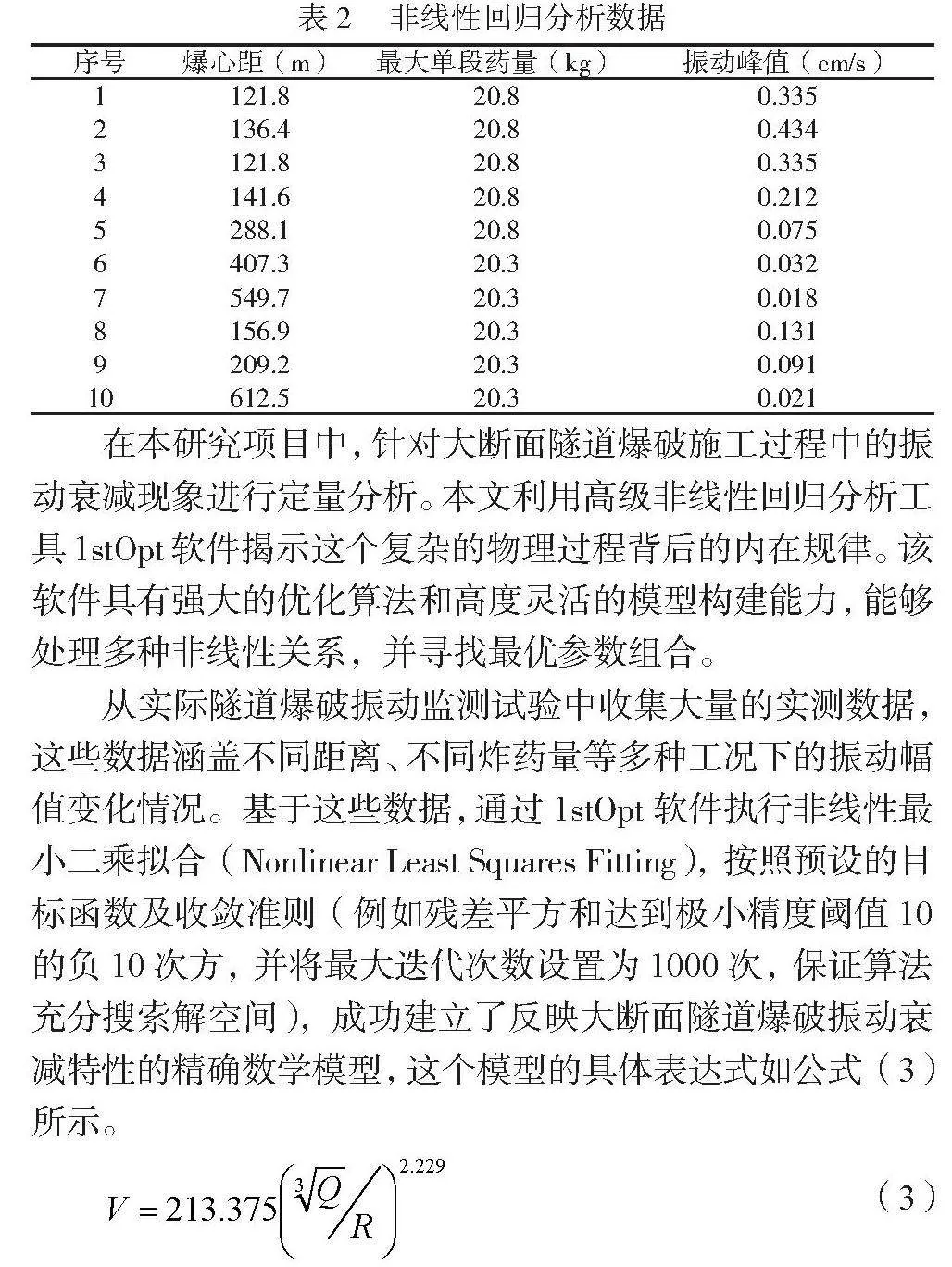
在本次研究工作中，运用专业的1stOpt非线性回归分析软件进行数据处理和建模。为保证模型优化的高效性和准确性，采用了麦夸特法（Marquardt's method）进行计算。在应用该方法的过程中，将收敛判断标准设定为残差平方和降至10的负十次方，同时将最大迭代次数设置为1000次，保证在合理计算资源下充分搜索最优解空间。在实际操作过程中，为了实时监控并控制计算过程，每进行10次迭代便会输出一次当前的控制数信息，以便于观察模型拟合度的变化趋势。此外，所有分析均遵循1stOpt软件的标准模式设置，保证结果的可靠性和可比性。针对爆破振动监测的数据集，选取具有代表性的局部数据进行深入研究，总纳入10组有效数据样本。对这些具体的数据进行整理，整理结果见表2。表中展示了各个炮孔爆破后的振动参数变化情况，将其作为本次非线性回归分析的基础数据来源，通过科学严谨的方法揭示大断面隧道爆破振动衰减规律及影响因素。

表2 非线性回归分析数据

序号 爆心距（m） 最大单段药量（kg） 振动峰值（cm/s）

1 121.8 20.8 0.335

2 136.4 20.8 0.434

3 121.8 20.8 0.335

4 141.6 20.8 0.212

5 288.1 20.8 0.075

6 407.3 20.3 0.032

7 549.7 20.3 0.018

8 156.9 20.3 0.131

9 209.2 20.3 0.091

10 612.5 20.3 0.021

在本研究项目中，针对大断面隧道爆破施工过程中的振动衰减现象进行定量分析。本文利用高级非线性回归分析工具1stOpt软件揭示这个复杂的物理过程背后的内在规律。该软件具有强大的优化算法和高度灵活的模型构建能力，能够处理多种非线性关系，并寻找最优参数组合。

从实际隧道爆破振动监测试验中收集大量的实测数据，这些数据涵盖不同距离、不同炸药量等多种工况下的振动幅值变化情况。基于这些数据，通过1stOpt软件执行非线性最小二乘拟合（Nonlinear Least Squares Fitting），按照预设的目标函数及收敛准则（例如残差平方和达到极小精度阈值10的负10次方，并将最大迭代次数设置为1000次，保证算法充分搜索解空间），成功建立了反映大断面隧道爆破振动衰减特性的精确数学模型，这个模型的具体表达式如公式（3）所示。

（3）

为进一步验证与可视化非线性回归模型的适用性和准确性，本文运用Origin科学绘图与数据分析软件对原始数据进行曲线拟合。在Origin中，导入实际监测到的振动衰减数据点，并采用建立的非线性回归模型进行曲线拟合操作，生成一条紧贴数据趋势且形态稳定的拟合曲线，该曲线生动地展示了爆破振动强度随着传播距离或其他相关变量的变化而逐渐衰减的过程。

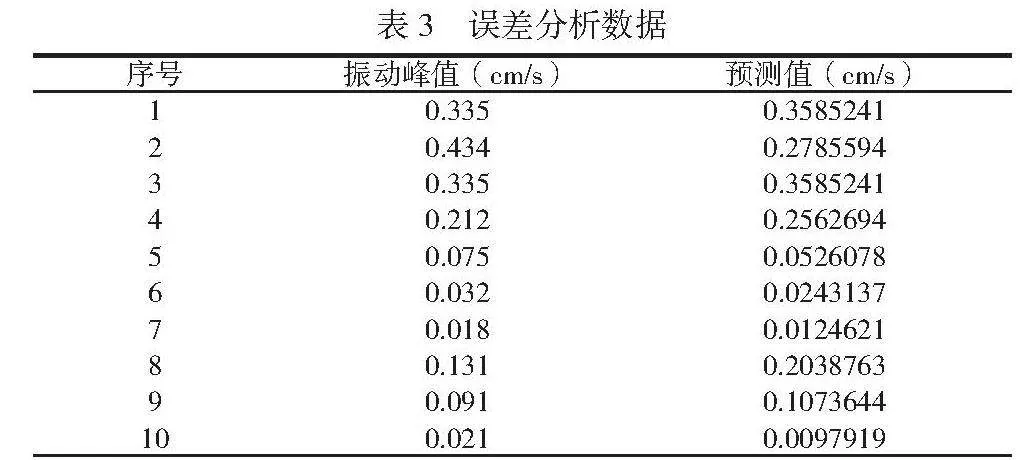
非线性拟合曲线的结果以图表形式呈现，如图1所示，不仅直观证实了使用1stOpt软件建立模型的有效性，还为后续类似工程实践预测和控制大断面隧道爆破引起的振动问题提供了可靠的理论基础和支持。误差分析数据见表3。

在本研究项目中，针对实际隧道爆破施工过程中产生的振动速度数据进行非线性回归分析。运用专业数据分析软件1stOpt对经典的萨道夫斯基公式进行参数优化与模型拟合。经过严谨的计算过程，将关键参数K设定为213.375，而α值为2.229。采用1stOpt软件进行非线性回归分析结果显示，该模型表现出良好的适应性和预测性能：均方根误差（Root Mean Square Error， RMSE）达到了0.0578，说明模型预测值与实际观测值之间的平均偏差度较小；残差平方和（Sum of Squared Errors， SSE）数值为0.033，表明模型整体上对数据集的拟合效果较为理想；相关系数高达0.915，这个结果揭示了模型预测值与实际观测值之间存在显著的正相关联系；决定系数为0.838，说明模型能够解释被观察变量变化的83.8%，具有较高的解释力；卡方系数（Chi-Square）仅为0.066，进一步证实了模型与实际数据之间具备高度的一致性。

表3 误差分析数据

序号 振动峰值（cm/s） 预测值（cm/s）

1 0.335 0.3585241

2 0.434 0.2785594

3 0.335 0.3585241

4 0.212 0.2562694

5 0.075 0.0526078

6 0.032 0.0243137

7 0.018 0.0124621

8 0.131 0.2038763

9 0.091 0.1073644

10 0.021 0.0097919

然而，当深入探讨非线性回归预测数据的误差分布时，尽管总体拟合效果良好，但在个别数据点上的预测误差范围较大，最大单点误差达到55.6%，最小误差为7.02%。

综上所述，对大断面隧道爆破振动监测数据进行非线性回归分析，并结合经典萨道夫斯基公式，得出结论：在一定程度上，萨道夫斯基公式确实可以用于大断面隧道爆破振动数据分析以及对未来爆破振动强度的预测工作。然而，鉴于存在局部预测误差问题，建议在实际应用中，根据现场实际情况进行修正调整或结合其他影响因素构建更为精确的预测模型。

4 结论

以实际隧道爆破工程为背景，根据地质资料提出上台阶爆破施工方案并且通过监测的爆破振动数据采用萨道夫斯基公式进行非线性回归分析，得出以下结论。1）根据实际隧道爆破资料，设计III级围岩爆破上台阶施工方案，炮孔共115个，装药量为220.48kg，单次隧道爆破开挖进尺约3m。2）在实际爆破施工过程中，对现场监测到的振动速度数据进行深入分析。利用专业的非线性回归分析软件1stOpt，对经典萨道夫斯基公式进行参数优化与模型拟合。

通过数据处理和计算，得出以下关键回归分析结果：萨道夫斯基公式的K值为213.375；将α值设定为2.229。

模型预测精度相关指标如下。1）均方差（Root Mean Square Error， RMSE）为0.0578，说明模型预测值与实际观测值之间平均偏差的大小。2）残差平方和（Sum of Squared Errors， SSE）为0.033，表明模型整体拟合度良好。3）相关系数为0.915，证明模型预测值与实际观测值之间的关联程度极高。4）相关系数平方（R²）即决定系数（Determination Coefficient， DC）为0.838，显示模型能解释原始数据变异性的83.8%。5）卡方系数（Chi-Square）仅为0.066，进一步验证了模型与实际观测数据的一致性。

通过上述非线性回归分析，本次研究成功建立反映大断面爆破振动衰减规律的数学模型。然而，当模型预测数据与实测数据进行对比时发现，最大误差达到55.6%，最小误差为7.02%。尽管模型在一定程度上揭示了爆破振动衰减的趋势，并具备较高的预测能力，但鉴于局部误差较大，在实际应用中仍须结合实际情况进行调整和完善，提高预测精确度及模型适用性。

参考文献

[1]孔宪军.基于 MATLAB的爆破震动研究及震动强度的智能预测[D].青岛：山东科技大学，2006.

[2]谢烽.施工隧道内部爆破振动效应研究[D].北京：中国矿业大学，2017.

[3]翟渊博.隧道爆破震动对民房的危害及安全评价[D].西安：西安建筑科技大学，2008.

[4]贾虎.爆破动载下邻近硐室围岩稳定性的研究[D].淮南：安徽理工大学，2006.

[5]朱传统，刘宏根，梅锦煌.地震波参数沿边坡坡面传播规律公式的选择[J].爆破，1988（2）：33-34.

[6]卢文波，张乐，周俊汝，等.爆破振动频率衰减机制和衰减规律的理论分析[J].爆破，2013， 30（2）：1-6.