云南某城市公共供水管网目标优化设计研究

摘 要：本文以城市公共供水管网为目标，探讨多目标优化设计方法在供水管网优化设计中的应用以及管网的总成本、可靠性等优化目标。采用多目标优化设计和蒙特卡洛模拟方法，通过构建目标函数和权重分配，生成备选设计方案，并利用理想点法进行综合评价，确定最优解。研究结果表明，基于多目标优化设计的方法能够全面考虑多个目标和约束条件，克服单目标优化的片面性，同时蒙特卡洛模拟方法能够有效克服优化设计的非线性及离散型。

关键词：多目标优化设计；供水管网；蒙特卡洛模拟

中图分类号：TU 991" " 文献标志码：A

1 工程概况

以云南某市的供水工程为研究对象，进行城市公共供水管网目标优化设计研究。该供水工程由27个供水节点组成，包括水源、泵站、调节水池、用户等。节点之间通过42个管段相互连接，形成一个复杂的供水网络。最高时总供水量为1267.34L/s，最不利点的自由水头为30m。管网的基准收益率为8%，运行维护费率为管网总成本的3.5%。项目计算期为30a，泵站各时段的综合效率为80%。此外，日变化系数为1.2，该数据反映供水需求在一天内的变化幅度。

2 多目标供水管网目标优化模型建立

为实现该城市公共供水管网的目标优化设计，采用一种分步骤的优化思路，包括初步流量分配、管段管径模拟、备选设计方案生成、目标函数计算以及综合评价确定最优解[1-2]。以下是详细的设计思路阐述。1）初步流量分配。采用最短路线法对供水管网中的各管线流量进行初步分配。通过计算各管线的阻力损失，将流量分配到各管线上，从而得到一个初步的流量分配方案。2）管段管径模拟。利用蒙特卡洛模拟方法对各管段的管径进行模拟。通过设定合理的管径范围和模拟次数，生成一系列可能的管径组合，为后续的优化设计提供备选方案。3）备选设计方案生成。根据蒙特卡洛模拟得到的管径组合，结合初步流量分配的结果，生成一系列的管网备选设计方案。4）目标函数计算。在生成备选设计方案后，将计算每个方案的目标函数值。目标函数通常包括多个优化目标，通过建立目标函数模型，对每个备选设计方案进行评估，得出各方案的目标函数值。5）综合评价确定最优解。采用理想点法进行综合评价，以确定最优解。通过比较各方案的综合评价函数值找出最优解。

3 确定最小路径

3.1 模型配置

为实现城市公共供水管网的目标优化设计，采用Dijkstra法计算最短路径，并基于此计算模型进行路径计算。

构建网络图：将供水管网抽象为一个加权有向图，如公式（1）所示。

G=（V，E） （1）

式中：V为节点集合；E为边集合。

节点V代表供水管网中的各个节点，边E代表供水管网中的各个管线。

初始化：设定一个初始节点作为源点，记为s。创建一个优先队列Q，用于存储待处理的节点及其距离。针对图G中的所有节点v，初始化距离d（s，v）为无穷大，源点s的距离为0。同时，创建一个集合S，用于存储已处理过的节点。

Dijkstra算法计算最短路径：利用Dijkstra算法计算从源点s到其他节点的最短路径。算法的主要步骤如下。1）将源点s加入集合S，表示已处理。2）针对集合S中的每个节点v，遍历其邻接节点u，计算从源点s经过节点v到节点u的路径长度alt，如公式（2）所示。3）如果alt小于当前已知的从源点s到节点u的最短路径长度d（s，u），就更新最短路径长度d（s，u）为alt，并将节点u的前驱节点设置为v。4）重复步骤2和步骤3，直到集合S囊括所有节点。

alt=d（s，v）+weight（v，u） （2）

式中：d（s，v）为从源点s到节点v的最短路径长度；weight（v，u）为边（v，u）上的权重。

计算最短路径：在Dijkstra算法计算完成后，可以得到从源点s到其他节点的最短路径长度d（s，v）。这些最短路径长度可以用于后续的流量分配和优化设计。

3.2 数据计算及分析

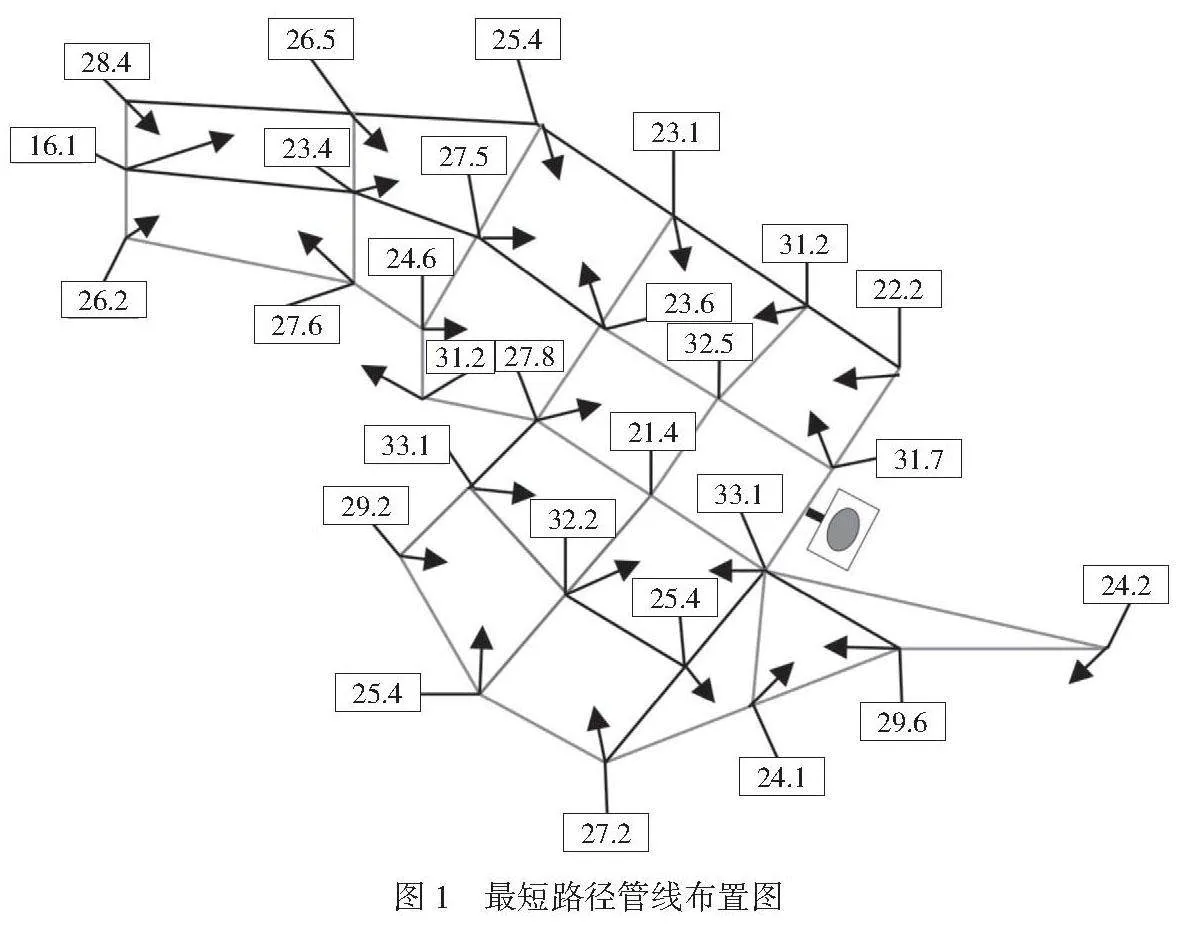
结合考虑供水管网的可靠性以及经济性，因为计算过程烦琐且数据量大，所以采用建模软件Matlab2018a进行模型计算，将供水管网数据进行导入按照公式（1）、公式（2），得出供水路线最短路径规划图（如图1所示）。在此选择部分规划点的数据进行计算。

3.2.1 步骤1

节点集合V={A，B，C，D，E}，边集合E={（A，B，2），（A，C，4），（B，C，1），（B，D，5），（C，D，3），（C，E，2），（D，E，2）}，（（A，B，2）表示从节点A到节点B的管线权重为2）。

3.2.2 步骤2：初始化

设定源点为A，即s=A。初始化距离，d（s，A）=0，d（s，B）=∞，d（s，C）=∞，d（s，D）=∞，d（s，E）=∞。优先队列Q={A（0）}，已处理节点集合S={}。

3.2.3 步骤3：Dijkstra算法计算最短路径

3.2.3.1 处理源点A

将A加入集合S，S={A}，遍历A的邻接节点B和C，更新距离，如公式（3）、公式（4）所示。

dlt=d（s，A）+weight（A，B）=0+2=2，更新d（s，B）=2" （3）

alt=d（s，A）+weight（A，C）=0+4=4，更新d（s，C）=4 （4）

更新优先队列Q={B（2），C（4）}。

3.2.3.2 处理节点B

从Q中取出距离最小的节点B，S={A，B}，遍历B的邻接节点C和D，更新距离，如公式（5）、公式（6）所示。

alt=d（s，B）+weight（B，C）=2+1=3，更新d（s，C）=3 （5）

alt=d（s，B）+weight（B，D）=2+5=7，更新d（s，D）=7 （6）

更新优先队列Q={C（3），D（7）}。

3.2.3.3 处理节点C

从Q中取出距离最小的节点C，S={A，B，C}，遍历C的邻接节点D和E，更新距离，如公式（7）、公式（8）所示。

alt=d（s，C）+weight（C，D）=3+3=6，更新d（s，D）=6 （7）

alt=d（s，C）+weight（C，E）=3+2=5，更新d（s，E）=5 （8）

更新优先队列Q={D（6），E（5）}。

3.2.3.4 处理节点D

从Q中取出距离最小的节点D，S={A，B，C，D}，遍历D的邻接节点E，更新距离，如公式（9）所示。

alt=d（s，D）+weight（D，E）=6+2=8 （9）

因为8大于当前的d（s，E）=5，所以不更新，更新优先队列Q={E（5）}。

3.2.3.5 处理节点E

从Q中取出距离最小的节点E，S={A，B，C，D，E}，节点E没有未处理的邻接节点，算法结束。

3.2.3.6 结果

从源点A到各节点的最短路径如公式（10）～公式（13）所示。

A-gt;B-gt;C-gt;D=880 （10）

A-gt;B-gt;C-gt;E=880 （11）

A-gt;C-gt;D=630 （12）

A-gt;C-gt;E=1120 （13）

4 管网备选设计方案

4.1 蒙特卡洛模拟

采用蒙特卡洛方法模拟各管段管径[3-4]，并生成管网备选设计方案。计算步骤如下。1）确定管径范围和模拟次数。管径范围可以根据管材、设计规范和工程经验来确定。2）生成随机管径样本。在确定管径范围和模拟次数后，采用蒙特卡洛方法生成随机管径样本。针对每个管段，根据预设的管径范围，随机生成一个管径值，如公式（14）所示。3）构建管网备选设计方案。根据生成的随机管径样本，构建一系列的管网备选设计方案。每个方案包括不同管段的管径选择，通过组合不同的管径，可以得到多种可能的管网布局。4）计算目标函数值。针对每个备选设计方案，计算目标函数值。重复模拟和评估，重复步骤2～步骤4，进行多次模拟和评估，以获得足够多的样本和评估结果。5）分析结果和确定最优解。在完成多次模拟和评估后，分析各备选设计方案的目标函数值，找出最优解。

Di～U（Dimin，Dimax） （14）

式中：Di为示第i个管段的管径；Dimin和Dimax分别为第i个管段管径的最小值和最大值；U为均匀分布。

4.2 数据计算及分析

通过蒙特卡洛模拟的计算步骤中公式（14），生成一个0～1的随机数Di。针对管段1，从最小的管径开始，累加被选概率，直到累加的和大于或等于Di。此时，累加到的管径就是被选中的管径。如果R=0.35，那么累加过程为0.032+0.057=0.089，0.089+0.185=0.274，由于0.274gt;0.35，因此选取的管径为600。重复步骤2，直到所有管段的管径都被选取，被选取概率见表1。

根据可供选择的管网管线被选管径概率划分至（0，1），以确定伪随机概率对应各管线管径之间的关系。基于此概念，使用Matlab2018a自带的蒙特卡洛模拟工具箱进行随机性模。

5 最优设计方案确定

5.1 理想点综合评价

采用理想点法进行综合评价，以确定最优解。详细计算步骤如下。1）确定优化目标。优化目标的数量可以根据研究需求和实际情况来确定。2）构建目标函数。针对每个优化目标，构建相应的目标函数，如公式（15）所示。3）计算目标函数值。针对每个备选设计方案，计算各个目标函数值。将决策变量x代入目标函数中，得到各方案的目标函数值。4）确定理想点和负理想点。理想点是指在每个目标函数上取得最优值的点，记为A*；负理想点是指在每个目标函数上取得最劣值的点，记为A-。理想点和负理想点分别如公式（16）、公式（17）所示。5）计算距离。计算每个备选设计方案与理想点和负理想点的距离。距离可以采用欧几里得距离来计算，如公式（18）所示。6）计算相对接近度。计算每个备选设计方案与理想点的相对接近度，如公式（19）所示。7）确定最优解。根据相对接近度Ci的大小，确定最优解。相对接近度最小的备选设计方案即为最优解。

fi（x）=（x-xi*）2 （15）

式中：fi（x）为第i个目标函数；x为决策变量；xi*为第i个优化目标的理想点。

A*=（x1*，x2*，…，xm*） （16）

A-=（x1-，x2-，…，xm-） （17）

式中：m为目标函数的数量。

d（A，B）=sqrt（（x1-y1）2+（x2-y2）2+…+（xm-ym）2）（18）

式中：A和B分别为2个点；xi和yi分别为2个点在第i个目标函数上的值。

Ci=d（Ai，A-）/（d（Ai，A*）+d（Ai，A-））" " " " " " （19）

式中：Ci为第i个备选设计方案与理想点的相对接近度；d（Ai，A*）和d（Ai，A-）分别为第i个备选设计方案与理想点和负理想点的距离。

表1 各管段管径被选取概率

管段编号 可选管径 被选概率

1 400 600 700 500 0.032 0.086 0.185 0.056

500 500 400 800 0.057 0.035 0.054 0.074

400 500 500 600 0.123 0.059 0.027 0.086

2 300 400 600 900 0.048 0.094 0.065 0.057

500 700 400 600 0.165 0.082 0.032 0.086

400 500 800 500 0.096 0.032 0.047 0.062

… 300 500 400 400 0.073 0.165 0.067 0.169

…

100 300 500 300 0.022 0.082 0.113 0.052

27 500 200 400 600 0.146 0.076 0.059 0.084

400 400 600 500 0.006 0.048 0.087 0.115

500 500 500 400 0.047 0.094 0.032 0.081

5.2 数据计算及分析

在理想点计算综合评价得分的基础上，分别选取主观赋权法FAHP法以及客观赋权法CRITIC法确定综合评价得分高的方案，在对比2种权重的基础上，选取年综合费用计算作为实例，对备选设计方案A进行综合评价，目标函数值f1（A）=

（300-250）2=2500。

针对节点水头均值，备选设计方案A的目标函数值f2（A）=

（20-25）2=25，依此类推，得到其他目标函数值。

理想点和负理想点A*=（250，25，…，25）A-=（350，15，…，15）。

针对备选设计方案A，与理想点的距离d（A，A*）=sqrt（（300-250）2+（20-25）2+…+（15-25）2）=100，与负理想点的距离d（A，A-）=sqrt（（300-350）2+（20-15）2+…+（15-15）2）=100，相对接近度CA=d（A，A-）/（d（A，A*）+d（A，A-））=100/（100+100）=0.5。

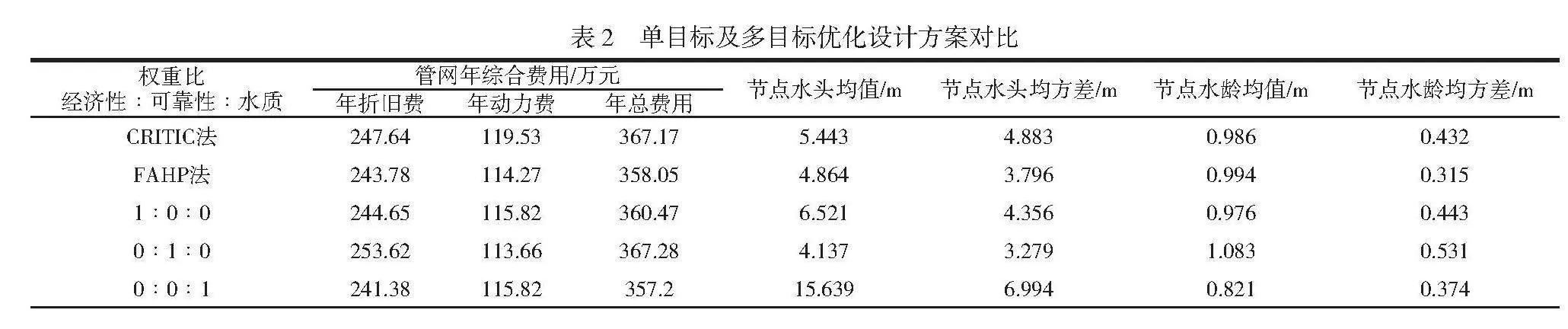
确定最优解：根据相对接近度Ci的大小确定最优解。相对接近度最小的备选设计方案即为最优解。进一步将其与多目标近似最优解进行多重对比确定。对比结果见表2。

根据表2并结合综合评价计算方法确定综合方案评分值为0.0038、0.0021、0.0042、0.0031和0.0033。其中，由主观赋权法FAHP法所确定的非劣解分数最低为最优方案。基于以上优化设计方案必选的方法可以有效避免因项目指标值的某一分项得分过高而造成忽略其他评价目标值过差的情况。

6 结语

本文以具体城市公共供水管网为研究对象，采用多目标优化设计方法进行目标优化设计，得出以下结论。1）多目标优化设计方法能够全面考虑供水管网的多个目标和约束条件，克服单目标优化设计的片面性。在优化过程中，同时考虑管网的总成本、泵站的能耗、管网的可靠性等多个目标，通过权重分配和目标函数的构建，实现了多个目标之间的均衡和协调。2）蒙特卡洛模拟方法能够有效地克服优化设计的非线性及离散型。通过模拟大量的随机样本，蒙特卡洛方法能够捕捉管径和流量的不确定性以及目标函数的非线性和离散型。这种方法可以更好地反映实际情况，提高优化设计的准确性和可靠性。3）基于多目标优化设计和蒙特卡洛模拟的方法，成功地生成一系列备选设计方案，并通过理想点法进行综合评价，确定了最优解。最优解能够使管网的总成本最低、泵站的能耗最小、管网的可靠性最高，实现多个目标的同时优化。

综上所述，基于多目标优化设计的城市公共供水管网优化设计可以为其他城市供水管网的优化设计提供借鉴和参考。

参考文献

[1]郑帅龙.基于多目标进化算法的城市雨水管网优化设计研究[D].西安：西安理工大学，2023.

[2]潘瑞军.基于遗传算法的污水管网布局优化方法设计[J].水利规划与设计，2023（6）：6-9，38.

[3]刘成荣.基于智能算法的供水管网水力参数反演与设计优化[D].保定：河北农业大学，2023.

[4]张利.基于LCC的农村供水管网优化设计研究[J].水利技术监督，2023（4）：95-98.