豆科牧草对煤炭废弃地修复效果的多元回归分析

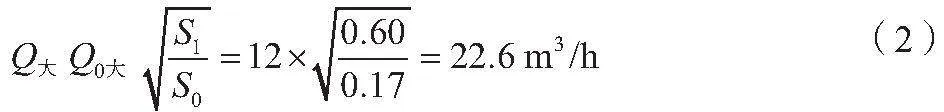
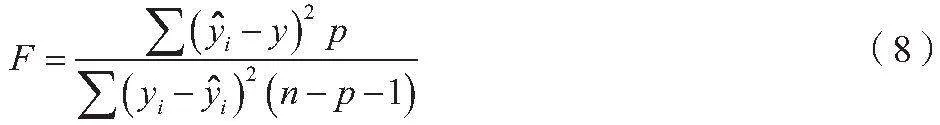
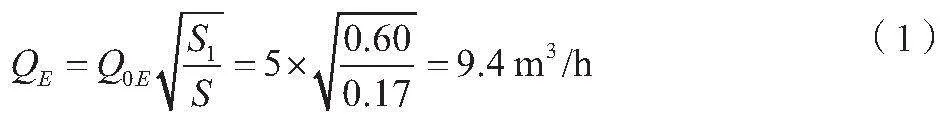
摘 要：矿区复垦和恢复生态环境对大气环境的长期影响十分显著。不仅可以防风固沙，而且还可以净化大气，增加降水。在煤炭弃耕复垦过程中，豆科牧草修复对煤炭废弃地的影响较大。本文以豆科牧草修复煤炭废弃地为研究对象，采用野外调查和室内模拟相结合的方法，结合资料分析、统计学分析，基于多元回归分析法，利用SPSS软件分析豆科牧草修复煤矿废弃地的试验情况。系统研究矿区弃耕地土壤理化性质、养分含量及植被的变化规律，揭示矿区弃耕地中豆类作物与土壤养分的相互作用机制，以期达到高效培肥、提升植被存活率的目的。

关键词：多元回归分析法；煤矿废弃地；SPSS

中图分类号：S 154 文献标志码：A

1 研究区域

本文对研究区域进行研究，判断水文地质条件，减少其他因素的影响，再进行试验分析，通过对照组（未进行豆科牧草修复）和观察组（进行豆科牧草修复）研究豆科牧草修复对煤矿废弃地的影响[1]。煤矿废弃地为亚热带季风湿润区，年均降水量1049mm，日最高降水量141mm（1964年5月20日），最大降水量445mm（1979年8月），5-9月份降水量68.4%，年均湿度88.5%[2]。煤矿废弃地利用豆科牧草修复了生态环境，从灾害的角度来看，治理煤矿废弃地的地质环境可以减少其对房屋、居民和煤矿废弃地周围交通的冲击，提高居民生活质量。优化了用地结构，遵循了宜林地不弃牧、草地宜牧的原则；其主要功能是减少土壤侵蚀、减少地表扬尘、改善煤矿废弃地生态环境。据调查，煤矿废弃地现在的正常涌水量为4m3/h，最大涌水量为11m3/h，基于矿井已开采的和还未开采的面积估算涌水量，煤层已采面积约为0.16km2，拟扩区和未开采的面积总共约为0.61km2。

预算增加的煤矿废弃地正常涌水量如公式（1）所示[3]。

预算增加的煤矿废弃地最大涌水量如公式（2）所示。

式中：QOE为矿井现在的正常涌水量，QOE=5m3/h；Q大为最大涌水量，Q大=12m3/h；S1为未开采的煤层面积[4]；S0为已开采的煤层面积。

经计算，煤矿废弃地正常涌水量为5+9.4=14.4m3/h，煤矿废弃地最大涌水量为12+22.6=34.6m3/h。

综上所述，矿井是裂隙充水矿床，煤矿废弃地水文地质条件比较简单。

2 研究思路分析

指标选取：煤矿废弃地为亚热带季风湿润区，牧草的种植密度根据试验要求而定，以每平方米3株为宜。

研究方法：为了提高豆科牧草修复煤炭废弃预测的精度，基于多元回归分析法，以可能影响豆科牧草修复煤炭废弃的累计土壤侵蚀情况设置对照组（未进行豆科牧草修复）和观察组（进行豆科牧草修复）。

研究软件：利用SPSS软件分析相关程度，并对其进行多元回归分析以及相关性分析，得到了豆科牧草修复煤炭废弃的相关数据，通过豆科牧草修复煤炭废弃实例进行验证。

3 相关算法

3.1 多元线性回归模型的一般形式

设随机被解释变量y与一般解释变量x1，x2，…，xk线性回归模型的标准形式如公式（3）所示[5]。

yi=β0+β1xi1+β2x2i+…+βkxki+ei （3）

式中：yi为被解释变量y的第i个观测值；xki为第k个解释变量xk的第i个观测值；β0，β1，β2，…，βk为模型的回归系数；ei为随机误差项。

3.2 多元线性回归模型的基本假设

要构建能够准确描述资产定价特征的统计模型，必须具备一系列重要的假设前提[6]。以上假设保障了模型的准确性和可靠性，为后续研究打下了坚实的理论基础。首先，本文提出“独立”假设，认为各个因素之间不存在相关性，这样就避免了共线性问题。其次，正常假设，也就是假设数据是正常的，这样就能确保数据的均值和方差是准确的。再次，本文将研究目标的可观测性假设，即所选取的参量可由直接观察而非间接获得，这是为了保证模式的适应性及预测效能，即采用最小二乘或极小偏估计量。基于该方法，本文从海量的数据中挖掘规则，并对其进行有效的预测，模型必须符合下面5个假设。1）解释变量x1，x2，…，xk非随机或固定，且各xk之间不存在严格线性关系[7]。2）样本中获得的每个解释变量xk都具有差异性，并且每个xk的σ2均约等于一个不等于零的常数。3）期望为0的ei，σ2相等并且没有序列相关性[8]。4）ei与xk之间没有关联。5）ei～N（μ，σ2），N为正态分布。

3.3 参数估计

3.3.1 回归系数的估计

在建立起精确的数学模型后，再根据已有的抽样资料对该模式中的一些不确定因素进行估计，包括回归系数和整体的标准偏差等。其中，常用的最小二乘法以其简单、精确等优点受到广泛关注，是目前公认的最典型的估算方式。该算法使各变量的方差的和达到最大，从而保证预报的准确性。一般最小二乘具有结构简单、便于理解和计算的特点，已逐渐被人们所接受。

小二乘法是最常用的一种估算方法，但这种方法需要有一个基础，由于某些原因，往往会造成模型与实际情况不符，于是提出了许多新的估算手段，例如主成分回归等，但这些都是建立在最小二乘法的基础上。

最小二乘法就是使残差平方和如公式（4）所示[9]。

3.3.2 样本方差的估计

多元线性回归模型中随机误差项ei的样本方差S2（S也为回归估计的标准误差，S越小说明回归方程的代表性越强）如公式（7）所示[6]。

3.4 模型检验

建立回归方程后，还必须进行各类统计检验，例如回归方程的R2检验、回归方程的F检验、回归系数的t检验。

3.4.1 回归方程的显著性检验

模型假设为H0：β1=β2=…=βp=0，H1：β1，β2，…，βp不全为0。

检验统计量如公式（8）所示。

式中：p为解释变量的个数；F统计量服从自由度（p，n-p-1）的F分布。

用统计软件自动计算检验统计量的观测值及相应的概率p值，如果plt;α，就应拒绝原假定，认为回归系数不全为0，表明回归方程具有显著意义；如果pgt;α，就相反。

3.4.2 回归系数的显著性检验

模型假设为H0：βi=0，H1：βi≠0。

构造检验统计量如公式（9）所示。

ti服从自由度为n-p-1的t分布。如果plt;α，就拒绝原假定，认为某一个回归系数不为0；如果pgt;α，就相反。

3.4.3 回归方程的拟合优度检验

在线性回归模型中，用判定系数R2表示拟合程度，如公式（10）所示。

为了避免因添加自变量而导致高估R2，通常也采用调整过的多重判定系数Ra2来进行拟合优度检验，如公式（11）所示。

R2或Ra2的值越接近1，说明拟合度越高，相反R2或Ra2越接近0，拟合效果越差。

3.5 模型预测

如果这一模型能够顺利地通过以上各种统计检验，那么可以用此模型对所诠释的变数进行预测。在确定目前各解释变量的样本量后，可以使用一个最优的回归模型对该变量进行处理，如公式（12）所示。

yf在给定显著性水平σ之下的置信区间如公式（14）所示。

式中：tα/2为显著性水平α的t分布双侧临界值。

4 豆科牧草修复煤炭废弃地结果分析

4.1 土壤pH值与豆科牧草修复相关性分析

通过表1可以了解不同时间段的土壤pH值不一致，但大体上的趋势是对照组比观察组高，而其随着时间观察组减轻迅速，对照组较缓慢，说明豆科牧草修复能够降低土壤pH值，有助于保护环境。

上述回归系数的显著性检验分析，P＜0.05表示有相关度，具有统计学意义，根据表1对照组是没有进行豆科牧草修复的一组，观察组为豆科牧草修复一组，观察组土壤pH值程度明显小于对照组，甚至144天以后土壤pH值大幅度减轻，豆科牧草修复对土壤pH值有明显效果，增加了煤炭废弃地修复率。

4.2 土壤元素与豆科牧草修复相关性分析

P＜0.05表示有相关度，T值表示显著性水平，具备统计学意义，土壤全氮、全磷、全钾、速效磷含量显著高于对照组（Plt;0.05），t值也随着豆科牧草修复有所变化，差距增大，也就是说对照组的全氮、全磷、全钾、速效磷含量因开采缘故或高或低，观察组更趋近于正常值，增加豆科牧草，有利于土壤环境趋向于正常水平，维护土壤平衡。

根据表2土壤元素与豆科牧草修复相关性分析研究显示，全氮含量相差不大，对照组76.12±8.34，观察组98.6±5.12，观察组全氮含量提高，而观察组的速效磷含量达到了50.08±0.34，对照组则为223.3±2.12，观察组的速效磷含量趋向平衡，说明土壤元素与豆科牧草修复具备相关性，P＜0.05，豆科牧草修复煤炭废弃地对全氮、全磷、全钾、速效磷含量有很大的影响。

4.3 回归分析

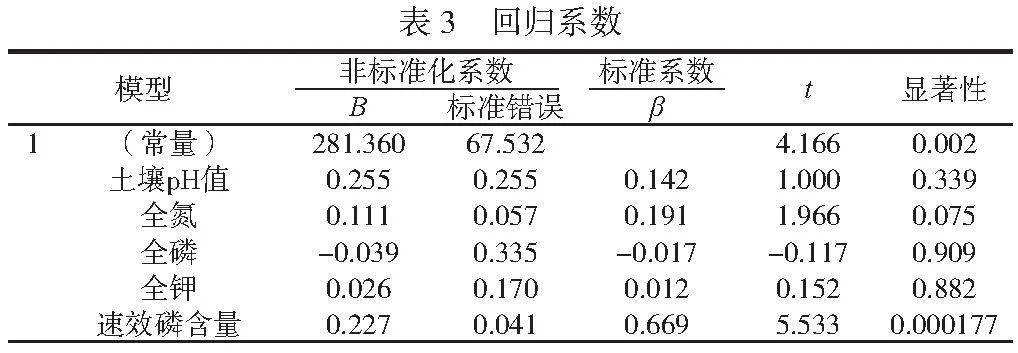
本文的统计分析工具是SPSS.22.0软件[5]，下面将收集的各项数据输入该软件中，设置默认的显著性水平α为0.05，得到的结果见表3。

5 模型检验

5.1 拟合优度检验

结合上述3.4.3回归方程的拟合优度检验中公式（11）所示，由表4可知，R2=0.999，调整后的可决定系数Ra2=0.998，两项数据接近1，表示该模型的拟合程度非常好，通过回归分析研究模型拟合程度，有利于分析数据的准确性，以便了解豆科植物对煤矿废弃地的影响，拟合优度表显示该试验相关影响因素具有良好的拟合程度，对实际需求更有帮助，其回归方程具有显著性，表明相关因素具有联系，也具备统计学意义。

5.2 回归方程的F检验

当F检验时，首先提出假设H0：β1=β2=…=β6=0，H1：β1，β2，…，β6不全为0。结合表5方差分析来看，在给定的显著性水平α=0.05下，可以得到自由度k-1=5和n-1=17对应的临界值为Fα（5，17）=2.8，而F=1855.933，因为F=1855.933gt;Fα（5，17）=2.8，所以拒绝原假设，表明回归方程显著，表明豆科牧草恢复煤矿废弃地起正影响，其相关数据也表明豆科牧草修复对煤矿废弃地各因素都是有影响的，其具有相关性，具备统计学意义。

5.3 回归系数的t检验

当t检验时，首先提出假设H0：βi=0，H1：βi≠0（i=0，1，2，…，6），根据表3可得初步多元线性回归模型中各个自变量系数的检验统计量值y=281.36+0.288x1+0.111x2+0.039x3+

0.026x4+0.257x5、p=（0.002）（0.039）（0.075）（0.009）（0.042）（0.000177）。在给定的显著性水平α=0.05下，只有x5对应的概率p值小于给定的显著水平α，表明在该模型中所研究的回归系数显著，豆科牧草修复效果是明显的，其实，根据初步多元线性回归模型中各个自变量系数的检验统计量值来看，通过多元线性回归方程使数据更具说服力，具备统计学意义。

从回归方程中可以看到，土壤pH值、全氮、全磷、全钾、速效磷含量与豆科牧草修复煤炭废弃地有正影响，豆科牧草修复煤炭废弃地是有效果的。

6 结语

结合上述分析，在利用豆科牧草进行复垦的过程中，对豆科牧草的试验结果进行比较发现，豆科牧草与未种植相比，通过相关性分析，观察组土壤pH值程度明显小于对照组，甚至在144d后，土壤pH值大幅度减轻，由土壤全氮、全磷、全钾、速效磷含量与豆科牧草修复相关性分析可知，土壤元素与豆科牧草修复具备相关性，p＜0.05，豆科牧草修复煤炭废弃地对全氮、全磷、全钾、速效磷含量有很大的影响。通过回归分析p=（0，002）（0.039）（0.075）（0.009）（0.042）（0.000177），在给定的显著性水平α=0.05下，豆科牧草能较好地适应煤矿废弃地土壤环境，而且在经过种植后，有了明显改善，其都能较好地适应煤矿废弃地土壤环境。在煤炭弃耕地恢复过程中，采用不同种类的豆类草地，可以在一定程度上达到培肥地力的目的。

参考文献

[1]李许娜.矿区废弃地的土壤特征与植被恢复研究[D].呼和浩特：内蒙古大学，2019.

[2]李强.8种植物在废弃煤矿植被恢复中的应用[J].防护林科技，2015，143（8）：22-23，45.

[3]施龙青，黄纪云，高卫富，等.多元线性回归在矿井断层延展长度预测中的应用[J].煤炭技术，2019，38（6）：71-73.

[4]青梅.基于回归分析的矿井监控数据挖掘分析[J].煤炭技术，2018，37（7）：260-262.

[5]杨辉.矿区废弃地植被恢复技术与实践[J].中国新技术新产品，2019，387（5）：120-121.

[6]郭云帅.煤矿废弃地环境重建与生态恢复[D].郑州：河南大学，2017.

[7]杨帅，高照良，白皓，等.矿山废弃地植物种植模式对土壤改良效果[J].水土保持学报，2017，31（3）：134-140.

[8]韩煜，赵伟，张淇翔，等.不同植被恢复模式下矿山废弃地的恢复效果研究[J].水土保持研究，2018，25（1）：120-125.

[9]周昊，郭娇娇，何绪文，等.煤矿区固废改良土壤对植物生长的影响[J].煤炭技术，2018，37（3）：23-25.