数控机床运动误差补偿方法研究

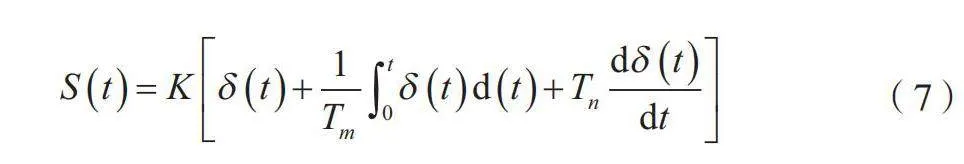
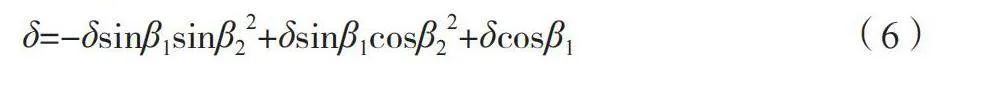
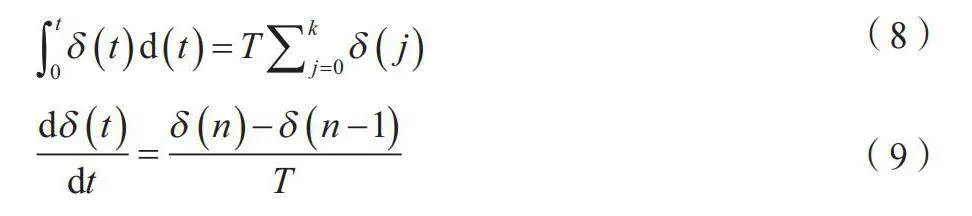
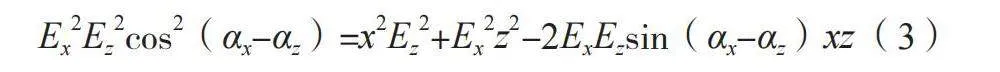
摘 要：在加工零部件过程中，常见的数控加工机床运动轨迹比较单一，也无法避免机床在加工过程中产生的运动轮廓误差，因此本文研究其运动误差补偿方法。本文介绍了目标数控机床的概况，在分析数控机床运动误差的基础上，提出基于比例积分微分（（Proportion Integration Differentiation，PID）控制的数控机床误差补偿方法。为了防止PID控制信号偏大或过小，提升运动误差补偿精确度，在PID控制器计算过程中引入粒子群优化算法。经仿真试验验证，使用效果良好，有效提升了数控机床的加工精度，最大程度避免了数控机床运动误差导致的产品加工质量下降。

关键词：数控机床；比例积分微分控制；粒子群优化算法

中图分类号：TG 519" " " " " " 文献标志码：A

随着人们的物质需求日益增长，制造业市场竞争日益激烈，零部件产品的加工精度和生产质量要求越来越高，但是多轴联控数控机床在加工零件过程中存在运动误差，因此制造行业需要增强该类机床的加工精度，提升产品质量，提高产品合格率。本文提出的基于比例积分微分（Proportion Integration Differentiation，PID）控制的数控机床运动误差补偿较为精准，不会由于机床速度加快而变大，还可以在不改变数控机床机械结构的前提下增强加工精度，效果较为稳定。该误差补偿方法缩短了精密零部件的加工周期，节约了投资成本，提升了产品质量。

1 数控机床概况以及测量原理

1.1 机床概况

目标数控机床结构如图1所示。在该数控机床（Computerized Numerical Control，CNC）系统中主要有X轴运动模块和Z轴2个运动模块。各运动模块均通过自身导轨与数控机床的床身连在一起，根据加工目标与机床相对运动的关系，机床误差划分为静态误差和动态误差。主轴旋转模块利用圆柱旋转来移动，与X轴、Z轴的平移运动一致，都是发生位移变化，因此其误差情况与X轴、Z轴的误差情况基本相同。装夹定位装置的作用是将镟修刀具和目标工件固定在CNC加工系统中，在加工过程中没有产生相对位移，因此一般归类为静态误差，对数控机床加工精度影响较小[1]。有研究表明，在数控机床的加工过程中，几何误差、热变形误差高达45%，在更精密机床的加工过程中，这2项误差占比会更高。本文主要研究CNC的几何误差。

1.2 测量原理

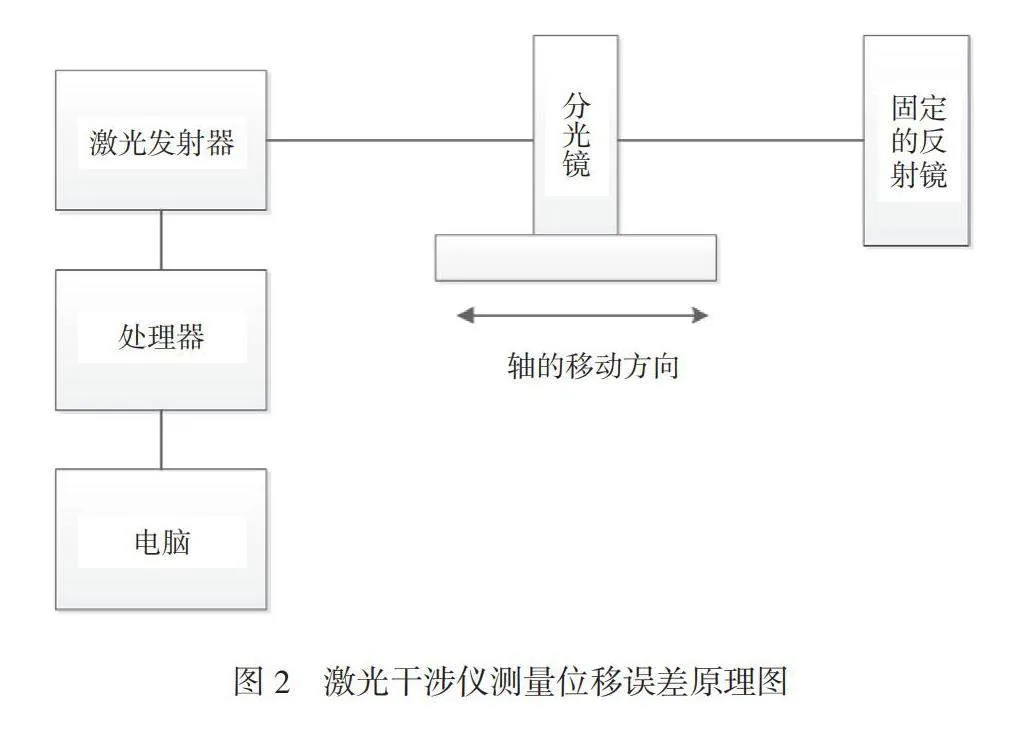
目标数控机床是由平东轴和主旋转轴组成的，本文只研究2个平动轴。精密CNC的加工精度要求比较高，运动误差数值较小，为了提高测量的有效性，在现场采用激光干涉仪、多普勒测量仪分别进行测量，前者测量位移误差，后者测量直线度误差（如图2、图3所示），当工作台上的反射镜发生位移时，激光发射器会感应光强度的变化，并利用处理器将运动误差信息上传至计算机，其测量精度为±0.4×106，数据读取频率为50 000 Hz，当机床高速运行时线性分辨率为1 nm，完全满足使用需求。

当数控机床存在位移误差以及直线度运动误差时，在X轴方向的平移运动轨迹中，每隔1 mm选取1个采样测量点，对该目标点位的位移误差和运动直线度误差分别进行有效采集。

2 数控机床运动误差分析

多轴联控数控机床应用广泛，在加工过程中，数控机床的的实际输出值与预期值存在一定偏差，当运动条件不同时，数控机床产生的误差也不同，在多轴联动状态下，数控机床极易产生运动误差。

X1（t）Ecos（wt）、" Z1（t）=Esin（wt）为目标数控机床x轴和z轴在加工程序中的输入，其对应的输出X2（t）、Z2（t）计算过程如公式（1）和公式（2）所示[2]。

X2（t）=Excos（wt-αx）" " " " " （1）

Z2（t）=Ezcos（wt-αz）" " " " " "（2）

式中：w为运动轨迹对应的角速度；Ex、Ez分别为x轴、z轴在加工系统中的输出值；αx、αz分别为x轴、z轴在加工系统中的滞后相位；t为任意时刻。

数控机床的运动理想模型如公式（3）所示。

Ex2Ez2cos2（αx-αz）=x2Ez2+Ex2z2-2ExEzsin（αx-αz）xz （3）

式中：x、z为运动轨迹对应的坐标点。

机床受其系统本身固有响应特性、信号控制和机械振动等因素干扰，会产生运动误差，该误差包括随动误差和外形误差[3]。随动误差为ΔSx、ΔSy、ΔSz，外形误差为ΔLx、ΔLy、ΔLz，如公式（4）、公式（5）所示。

∆S=∆Sx+∆Sy+∆Sz " " " " " " " " " " " " " " " " " "（4）

∆L= ∆Lx+∆Ly+∆Lz=-δsinβ1sinβ2+δsinβ1cosβ22+δcosβ1" " （5）

式中：β1、β2为任意时刻t运动位置与Z轴之间对应的夹角。

目标机床运动误差δ如公式（6）所示。

δ=-δsinβ1sinβ22+δsinβ1cosβ22+δcosβ1" " " " " " （6）

3 基于PID控制的目标机床运动误差补偿

采用PID控制对数控机床运动误差进行科学补偿[4]。将运动误差δ（t）作为PID控制器的调节对象，在PID控制器中对δ（t）进行积分、微分等变换，得到控制信号S（t），如公式（7）所示。

（7）

式中：Tm、Tn分别为PID控制器的积分和微分时间常数；K为比例系数；d（t）为对时间 t 的积分。

采用随机取点方式连接运动误差曲线上的任意2个点，用斜率表示PID中的微分，用矩形面积表示PID中的积分，如公式（8）、公式（9）所示。

（8）

（9）

式中：δ（j）为机床的运动偏差函数；j 为采样点；k为样本容量；δ（n-1）、 δ（n） 分别为第 n-1个采样时间点和第n个采样时间点CNC的运动偏差；T为采样周期，t=nT。

为了防止PID控制信号偏大或过小，须提高运动误差补偿精确度，在PID控制器计算过程中加入粒子群优化算法，其流程如图4所示。

在第四步中，在粒子寻优得到最佳位置Migood、Mzgood后，经过相关处理后获得相关的适应度值Nigood、Nzgood。当Nilt;Nigood时，Nigood=Ni，Migood=Mi；当Nilt;Nzgood时，Nzgood=Ni，Mzgood=Mi。满足这些条件后，完成粒子速度更新[5]。

4 CNC运动误差补偿仿真

为了测试本文所提误差补偿方法的使用效果，在VC++语言环境中验证CNC运动误差补偿，机床基本参数：主轴通孔直径为55 mm；X轴运动行程为26 mm；Z轴运动行程为25 mm；刀架定位精度为-3.0～3.0。

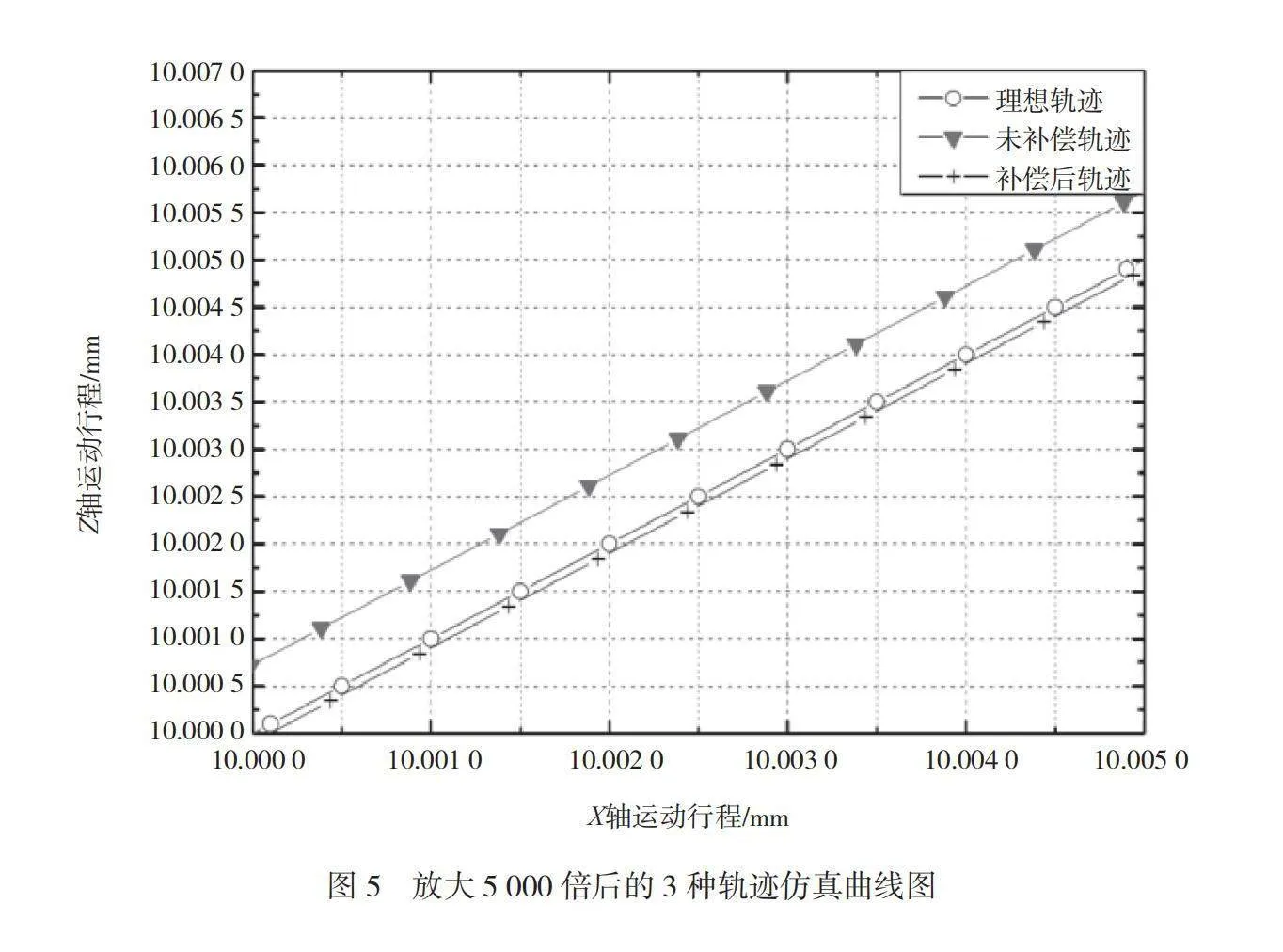
为了便于分析，当选择研究加工路径时，计算相应的误差补偿。利用PID误差补偿方法仿真数控机床加工运动轨迹，为避免3种轨迹重合，将曲线放大5 000倍（如图5所示），经过PID误差补偿方法补偿后的CNC运动轨迹轮廓显著逼近理论轨迹曲线，未做任何补偿的运动轨迹与理论曲线之间产生较大偏离，因为本文使用PID控制的误差补偿方法，利用粒子群算法对PID控制器进行了优化，所以减少了CNC机床在加工过程中由各种颤动引发的误差。

5 结语

本文介绍了数控机床的组成以及测量误差原理，对多轴联动数控加工机床运动进行误差分析，提出PID控制误差补偿方法，为了防止PID控制信号偏大或过小，在计算过程中采用粒子群优化算法，并进行现场验证，有效减少了机床运动误差，提升了加工精度，对后续多轴联动数控机床运动误差补偿方法研究起到了推动作用，促进了制造业健康发展。

参考文献

[1]张雷，刘检华，庄存波，等.基于数字孪生的多轴数控机床轮廓误差抑制方法[J].计算机集成制造系统，2021，27（12）：3391-3402.

[2]吴天凤，李莉，杨洪涛.数控机床XY 工作台单向运动二维阿贝误差分析与建模[J].光学精密工程，2021，29（2）：329-337.

[3]陈维范，薛丹.数控车床热误差建模与补偿研究[J].机床与液压，2020，48（14）：171-175.

[4]郭世杰，武建新，乔冠，等.数控机床几何误差正弦低次多项式参数化建模与应用研究[J].仪器仪表学报，2020，41（10）：136-146.

[5]蓝益鹏，姚婉婷，杨文康，等.数控机床直线同步电动机磁悬浮系统的神经网络直接自适应控制[J].机械工程学报，2021，57（17）：236-242.