基于改进鲸鱼优化算法的车间布局优化模型及其应用

摘 要：为提升车间作业效率，克服传统系统布置设计（System Layout Planning，SLP）方法过度依赖经验的缺点，本文构建了以最小化搬运成本和最大化作业单元非物流关系为目标的车间布局优化模型。鉴于问题的复杂性，设计了改进鲸鱼优化算法（Improved Whale Optimization Algorithm，IWOA）对其进行求解。仿真结果表明，IWOA优化后的布局显著提升了车间各作业单元布局的合理性，提高了作业效率。

关键词：改进鲸鱼优化算法；车间设施；布局优化

中图分类号：TB 49" " " 文献标志码：A

随着市场竞争的加剧，制造企业如何充分利用车间现有资源，采用合理、有效的车间布局方案，减少搬运时间、提高生产效率并降低成本成为一个备受关注的议题。

在长期发展中，车间布局优化中具有代表性的SLP方法出现效率低且准确性差的缺点[1]。目前，智能算法成为车间布局优化的重要工具[2]，文献[1]开发了一种遗传算法（Genetic Algorithm，GA）对车间布局优化问题进行求解。文献[2]使用GA与和声优化的混合算法对车间布局进行优化。文献[3]开发了一种自适应遗传模拟退火算法，获得车间布局优化的最优解。此外，候鸟优化算法[4]、粒子群算法[5]和人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[6]在车间布局优化中也逐渐得到了应用。

尽管智能算法在车间布局优化领域得到了有效应用，但根据没有免费午餐的理论[7]，没有一种算法可以解决所有优化问题，总有一种算法会表现出更优异的性能，有必要根据特定问题不断开发和改进新的算法。鲸鱼优化算法（Whale Optimization Algorithm，WOA）作为最新涌现的尖端算法，具有操作简单、稳定性强等优点[8]，但其在车间布局优化的应用较少。因此，本文设计了基于IWOA的车间布局优化模型。

1 车间布局优化数学模型

1.1 目标函数

针对车间布局优化问题特性，以最小化搬运成本（f1）和最大化非物流关系指数（f2）为目标，构建车间空间布局优化模型。搬运成本如公式（1）所示，由作业单元间的搬运成本、搬运量和距离的乘积计算得出。公式（2）表示的是非物流关系指数，由作业单元间非物流关系的紧密程度和关联因子的乘积计算得出。

（1）

式中：cij为作业单元i与j间的搬运成本；fij为作业单元i与j间的搬运量；dij为作业单元i与j间的距离，采用曼哈顿距离进行表示，dij=|xi-xj|+|yi-yj|；M为车间中的作业单元总数。

（2）

式中：Tij为作业单元i与j非物流关系的紧密程度；bij为作业单元i与j非物流关系等级与距离的关联因子。

为方便处理，将其转换为单目标函数。由于量纲不同，对其进行标准化，分别如公式（3）、公式（4）所示。

（3）

式中：dmax为任意2个生产设备间的最大距离；cij为作业单元i与j间的搬运成本；fij为作业单元i与j间的搬运量；dij为作业单元i与j间的距离，采用曼哈顿距离进行表示，dij=|xi-xj|+|yi-yj|；M为车间中的作业单元总数。

（4）

式中：Tij为作业单元i与j非物流关系的紧密程度；bij为作业单元i与j非物流关系等级与距离的关联因子；M为车间中的作业单元总数。

在公式（3）中，将搬运成本除以任意2个生产设备间的最大距离、作业单元间的搬运成本和作业单元间的搬运量的乘积，得到标准化搬运成本。在公式（4）中，将非物流关系指数除以作业单元间非物流关系的紧密程度的总和，得到标准化的非物流关系指数。

然后将公式（3）、公式（4）相结合构建单目标函数。在该函数中引入2个权重参数Z1和Z2，分别表示总搬运成本和非物流关系所占的权重，如公式（5）所示。

minF=Z1f *1-Zf *2 " " （5）

式中：Z1为总搬运成本所占权重；Z2为非物流关系所占权重。

1.2 约束条件

为了更贴近现实作业，对上述目标设定约束条件，如公式（6）～公式（11）所示。

（6）

式中：xi、xj为作业单元i和j的X轴中心坐标；li、lj为作业单元i和j的长度；s为作业单元间的最小间距。

（7）

式中：yi、yj为作业单元i和j的Y轴中心坐标；wi、wj为作业单元i和j的宽度；s为作业单元间的最小间距。

（8）

式中：xi为作业单元i的X轴中心坐标；li为作业单元i的长度；s为作业单元间的最小间距。

（9）

式中：yi为作业单元i的Y轴中心坐标；wi为作业单元i的宽度；s为作业单元间的最小间距。

（10）

式中：xi为作业单元i的X轴中心坐标；L为作业车间的长度；li为作业单元i的长度；s为作业单元间的最小间距。

（11）

式中：yi为作业单元i的Y轴中心坐标；W为作业车间的宽度；wi为作业单元i的宽度；s为作业单元间的最小间距。

在上述约束中，公式（6）、公式（7）可确保作业单元间有适当的间距。在X轴和Y轴上，任何2个作业单元i和j的中心坐标的差的绝对值应大于或等于它们的长度或宽度之和的一半加上最小间距s。公式（8）、公式（9）可确保各作业单元与车间墙壁间有足够的距离。在X轴和Y轴上，每个作业单元i的中心坐标应大于或等于它的长度或宽度的一半加上最小间距s。公式（10）、公式（11）避免了各作业单元超出车间的长度或宽度。在X轴和Y轴上，每个作业单元i的中心坐标应小于或等于车间的长度L或宽度W减去该作业单元的长度或宽度的一半和最小间距s。

2 改进鲸鱼优化算法

WOA算法是一种高效的群智能优化算法，在非线性函数寻优任务中表现出色。该算法拥有诸多优点，但同时也存在不足[9]。为有效优化上述问题，本文引入非线性递减收敛因子和随机差分变异策略对WOA进行改进，具体步骤如下所示。

2.1 种群初始化

为形成符合约束的初始个体，以基于坐标的方式表示车间各作业单位位置。将作业单元逐个放入车间，并在放入过程中检查其是否满足约束条件。如果放置不符合约束条件，进行重新放置，直至生成符合满足约束的个体为止。

2.2 包围猎物

包围猎物是IWOA重要的寻优环节[10]。采用公式（12）执行，鲸鱼的新位置x（it+1）由当前全局最佳猎物位置x*it减去距离向量D和控制因子A的乘积计算得出。

x（it+1）=x*it-AD " " （12）

距离向量D的计算过程如公式（13）所示，由鲸鱼的当前位置x（it）和当前全局最佳猎物位置xit*的差经过一个比例系数C缩放求得。C是根据公式（14）得到的常数，是一个随机数r2的2倍，r2在（0，1）随机产生。

D=|Cxit*-x（it）| " （13）

式中：it表示当前迭代次数，xit*表示当前全局最佳猎物位置；x（it）表示鲸鱼的当前位置；D表示鲸鱼与猎物间的距离向量。

C=2·r2 （14）

式中：r2为（0，1）随机产生的数。

控制因子A的计算过程如公式（15）所示，由线性递减的控制参数a和一个随机数r1的乘积减去a求得。控制参数a的值由公式（16）计算得出。

A=2a·r1-a " （15）

式中：r1为（0，1）随机产生的数；a为从2线性递减至0的控制参数。

（16）

式中：it表示当前迭代次数；maxit为算法最大迭代次数。

在WOA中，a按照固定速率下降，这会降低算法寻优精度[11]。因此，IWOA引入非线性递减收敛因子控制a的动态调整，其计算方式如公式（17）所示。公式（17）是一个分段函数，它的值取决于随机数rand是否小于或等于控制系数Pc。公式（17）的结果会随迭代次数增加而递减，但递减速度会随迭代次数的增加而减慢，最终使控制参数a的下降速率可以动态调整。

（17）

式中：it表示当前迭代数；maxit表示最大迭代次数；Pc为控制系数，Pc∈[0，1]；rand为[0，1]的随机数。

通过上述动态调整，可以有效提升IWOA的收敛速度和全局搜索能力。

2.3 泡泡网攻击

包围猎物完成后，IWOA进入泡泡网攻击阶段。该阶段通过摇摆包围和螺旋吐泡2种独特的机制进行[12]。1）摇摆包围。该机制与包围猎物具有很高的相似性，区别在于A的取值被调整为（-1，1）。2）螺旋吐泡。在该阶段，鲸鱼先测量自身与猎物（截至目前的最佳位置）间的距离。然后采用螺旋状的方式向上游移动，并释放各种大小的气泡以捕获鱼虾。该行为的数学模型如公式（18）所示。

x（it+1）=Dp·ebl·cos（2πl）+x*it （18）

式中：Dp=|x*it-xit|，通过计算自身与当前最佳猎物的距离获得；ebl和cos（2πl）共同构成了一个螺旋形的路径，其中b是一个表示螺旋形常数的参数，被设置为2，l是在（-1，1）随机生成的数，用于控制螺旋的方向和紧密度；x*it表示当前全局最佳猎物位置；it表示当前迭代次数。

上述两种攻击方式在IWOA中被选择的概率是相等的，即50%。

2.4 随机搜寻猎物

此外，IWOA会根据A值进行猎物的随机搜索。当|A|≥1时，新位置x（it+1）由随机选择的鲸鱼的位置xrand减去距离向量D和控制因子A的乘积求得，如公式（19）所示[10]。

x（it+1）=xrand-AD " （19）

式中：xrand为当前种群中随机选择的鲸鱼；A通过公式（15）计算得出；D通过公式（20）计算得出；it表示当前迭代次数；x（it+1）表示更新后的鲸鱼位置。

距离向量D的计算过程如公式（20）所示。

D=|Cxrand-x（it）| " （20）

式中：xrand为当前种群中随机选择的鲸鱼；C通过公式（14）求得；it表示当前迭代次数；x（it）表示鲸鱼的当前位置。

2.5 随机差分变异策略

为了进一步提升寻优精度，IWOA引入随机差分变异策略对种群进行再次搜索，如公式（21）所示。新的鲸鱼位置x（it+1）是鲸鱼向全局最佳猎物位置和随机选择的鲸鱼位置移动的综合结果：r1×（x*it-x（it+1））描述了鲸鱼向全局最佳猎物位置的移动，r2×（xrand-x（it））描述了鲸鱼向随机选择的鲸鱼位置的移动。

x（it+1）=r1×（x*it-x（it+1））+r2×（xrand-x（it）） （21）

式中：r1和r2为（0，1）的随机数；xrand为当前种群中随机选择的鲸鱼；it表示当前迭代次数；x（it）表示鲸鱼的当前位置；x（it+1）表示更新后的鲸鱼位置；xit表示当前全局最佳猎物位置。

需要指出的是，经过优化后的方案可能不符合约束，本文采用罚函数对其进行处理。

3 实例分析

以A公司车间布局为例说明算法和模型的有效性。该车间长度为180m，宽度为80m，共14个作业单元，各作业单元尺寸见表1。

关联因子bij设定见表2。表2可以具体量化非物流关系等级与距离间的数值关系。

各作业单元非物流关系紧密程度Tij如公式（22）所示，行和列代表作业单元，数字量化了各作业单元间的非物流关系紧密程度。

（22）

各作业单元搬运成本cij如公式（23）所示，行和列同样代表作业单元，数字量化了各作业单元间的搬运成本。

（23）

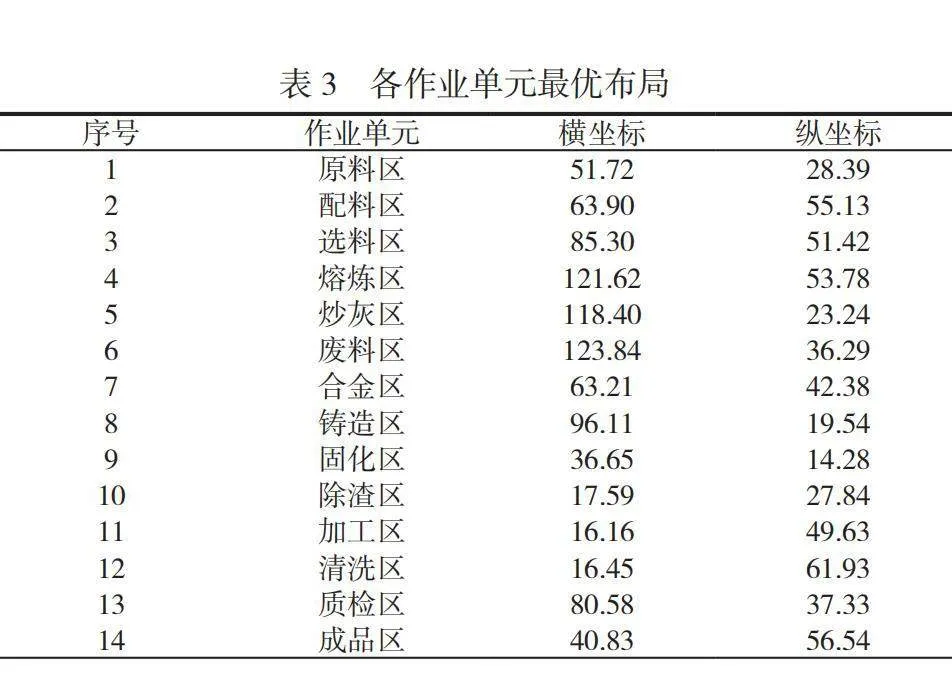
经文献分析和预试验，设定s=2，Z1=，Z2=，maxit=500，Npop=200，pc=0.4。程序运行一次，各作业单元坐标分布情况见表3。在当前布局下，所求最优结果为f1=53875.40，f2==21.80，F=0.0077。

4 IWOA性能分析

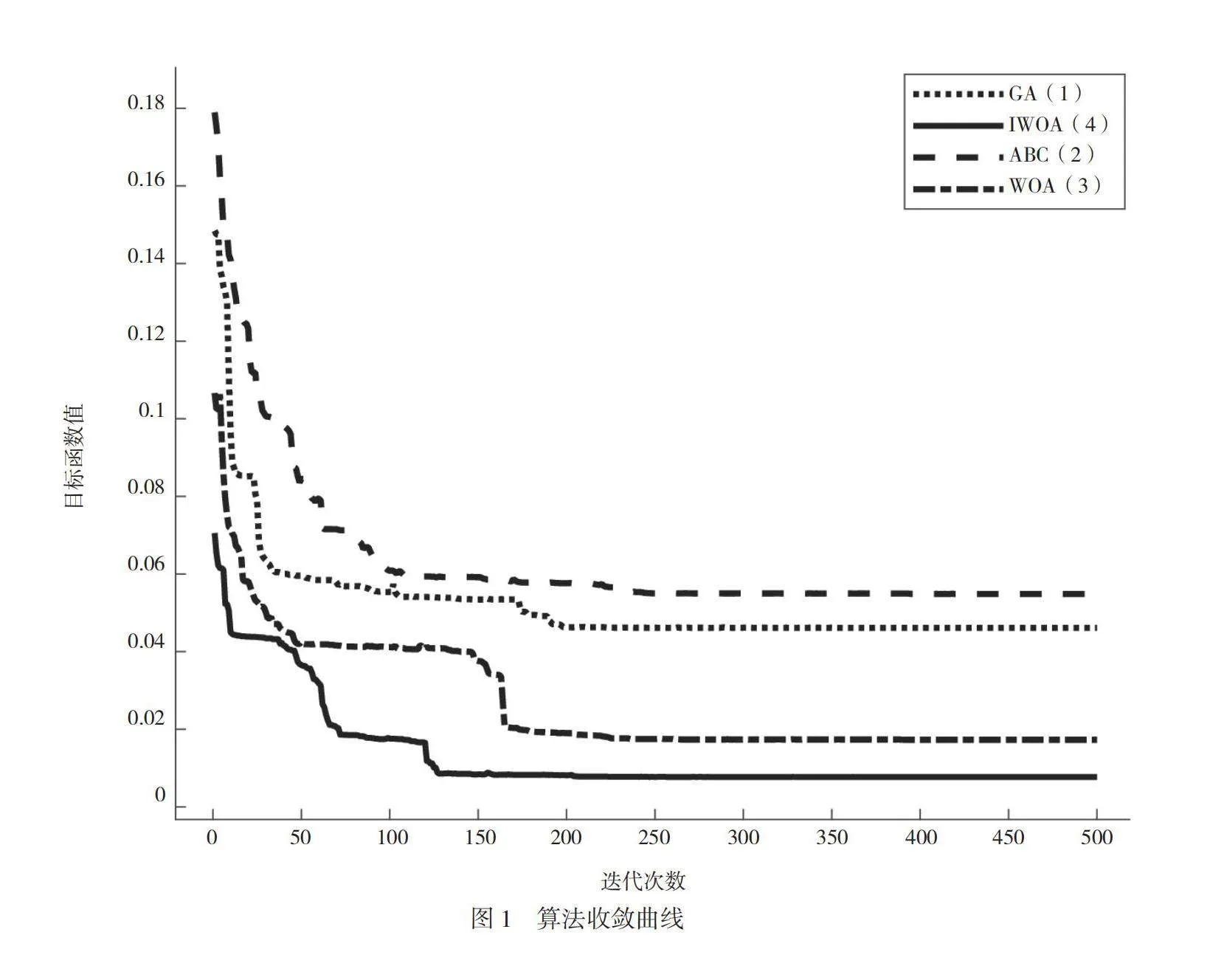
为了验证IWOA有效性，选取GA、WOA和ABC对上述案例进行求解。4种算法的优化曲线如图1所示。图1中，括号内的数字为从上向下代表该算法收敛情况的曲线的顺序。为确保公平，所有算法设定相同的迭代次数和种群规模，其他参数通过预试验和文献分析设定。可以看到IWOA和求解精度明显优于其他3种算法，尽管GA的收敛速度比IWOA稍高，但其精度远低于IWOA。

5 结论

本文针对车间布局优化问题构建了相应的优化模型，并设计IWOA进行模型求解。实际案例表明，IWOA在车间布局优化方面效果显著，能够有效提升车间布局的效率和性能。与其他算法相比，IWOA展现出了其优越性，为解决车间布局优化问题提供了一种有效途径。

参考文献

[1]姚明钊，陈鹏飞，裴小兵.基于SLP和改进遗传算法优化C企业车间布局[J].有色金属工程，2023，13（9）：99-109.

[2]郑广辉，钱叶昶，刘鹏，等.基于遗传和声算法的复兴号部件生产车间布局研究[J].机床与液压，2023，51（4）：57-62，66.

[3]卢义桢，李西兴，朱传军，等.基于自适应遗传模拟退火算法的多目标车间布局优化[J].制造技术与机床，2022（7）：173-179.

[4]张思奇，于登辉，郑一明，等.基于多目标候鸟算法的车间布局研究[J].现代制造工程，2022（2）：16-23.

[5]徐晓鸣，邓裕琪，吴绮萍.基于SLP和粒子群算法的车间布局优化研究[J].机电工程技术，2020，49（2）：17-20，98.

[6]汪和平，杨子沫，陈梦凯.基于人工蜂群算法的预制件厂平面布局优化[J].系统工程，2021，39（5）：143-151.

[7]WOLPERT D H，MACREADY W G.No free lunch theorems for optimization[J].IEEE transactions on evolutionary computation，1997，1（1）：67-82.

[8]许德刚，王再庆，郭奕欣，等.鲸鱼优化算法研究综述[J].计算机应用研究，2023，40（2）：328-336.

[9]李冰.改进鲸鱼算法优化GRU的大坝变形预测研究[D].赣州：江西理工大学，2023.

[10]SEYED MOSTAFA BOZORGI，SAMANEH YAZDANI.IWOA：An improved whale optimization algorithm for optimization

problems[J].Journal of Computational Design and Engineering，2019，6（3）：243-259.

[11]闵聪，桂海霞，张辉.基于改进鲸鱼算法的冷链配送路径优化[J].河南科技学院学报（自然科学版），2023，51（4）：76-84.

[12]郭权杰.基于CEEMDAN-LSTM模型的短期负荷预测研究与应用[D].天津：天津理工大学，2023.