基于改进NSGA-Ⅲ的低碳柔性作业车间调度优化

摘 要：随着环境保护意识的提高和低碳经济蓬勃发展，碳排放成本逐渐成为企业决策中必须考虑的重要因素。为实现碳排放成本、完工时间、拖期时长和机器负荷４个优化目标，本文建立了碳排放成本的高维目标柔性车间调度优化模型，并根据模型特点设计了一种基于生物激素调节机理的改进NSGA-Ⅲ算法。采用MATLAB软件对实际生产数据进行模拟仿真，证明所提出的优化方法可在保证完工时间和总拖期时间不受影响的情况下，控制碳排放成本、提高设备效率，同时满足工件加工工序的要求。

关键词：碳排放成本；遗传算法；高维目标优化；柔性流水车间调度；低碳经济

中图分类号：TP 18" " " 文献标志码：A

随着柔性作业车间调度问题复杂性增加，采用多目标智能优化算法求解成为主流。范雅男[1]等人将改进粒子群优化算法应用到柔性流水车间调度问题中。WU[2]等人采用启发式算法优化带设备开关机与调速2种节能手段的设备能耗模型。LIU等[3]提出了改进合作粒子群算法，该算法求解规模比较大的生产调度问题的收敛速度更快，质量更高。杨冬婧[4]等人以总延迟时间最小化为目标，将作业车间能耗约束转化为最小总能耗，建立车间调度模型，并设计了一种新型蛙跳算法。李丹[5]等人在遗传算法中引入一种基于个体斜率的改进精英选择方法，以求解高维目标柔性作业车间调度问题。宋佳容[6]等人使用3种邻域规则改进的蚁群算法，求解以最大加工收益和最小碳排放总量为目标的柔性车间调度问题。尽管上述研究证明优化作业车间调度与绿色生产具有重要联系，但上述研究较多关注优化车间能源消耗与作业完工时间，如何进一步约束车间碳排放成本仍值得研究。

本文探讨碳成本约束下，生产车间总碳排放成本在生产调度优化中的应用前景和挑战，以进行最佳碳成本控制和资源配置。

1 短期碳排放成本模型

碳排放总成本由预防成本、鉴定成本、有形损失成本和无形损失成本组成。碳排放成本和生产经济效益间相互影响。鉴于碳排放成本的存在，生产企业会更关注环境保护和资源利用效率，并应用清洁、高效的生产技术来降低碳排放。低碳势必会提升企业的竞争力，但也会增加运营成本。生产企业通常采取节能减排、资源循环利用、优化产品设计和使用先进管理办法或环保设备等措施应对碳排放量和碳排放成本的增加。

根据文献[7]中提出的短期碳排放成本决策模型可知，二氧化碳排放总成本为一条“U”形曲线，曲线上存在碳排放成本的最小极值点，该点上的碳排放量即经济碳排放量。在碳排放成本的最优点上，生产企业能够实现碳排放量和成本间的最佳平衡。因此，寻找并实现经济碳排放量是目前作业车间调度优化的重要目标之一。

2 作业车间调度模型

2.1 问题描述

本文研究的高维目标低碳柔性车间调度问题是将车间生产二氧化碳排放导致的成本、最大完工时间、总拖期时间以及加工设备总负载为目标函数的综合优化问题，可描述为共有n个需要依次经过不同s道工序才能完成的待加工作业，并且这些作业的工序可在m台机器中的多台上进行；不同工序和机器组合的加工时间是已知的且有差异（徐宜刚、陈勇和王宸等，《改进NSGA-III求解高维多目标绿色柔性作业车间调度问题》）。显然不同组合方案下的机器总负荷、最大完工时间、碳排放总量和碳排放成本有明显差异。低碳柔性车间调度优化的目标是在保证工件工序顺序进行的情况下，每个工件能够合理分配加工机器，以期找到经济碳排放量，使碳排放成本最低，同时将最大完工时间最小化，使总拖期最短且机器总负荷最低。该问题中有如下8个限制条件：假设1，所有作业是互相独立的，不存在先后顺序；假设2，任意作业均需要经过完整工序；假设3，任意工件的任意工序在同一时间只能由一个机器执行；假设4，一个工序可以在多台机器上处理；假设5，任意机器在同一时间只能执行一个工件的一个工序；假设6，在操作过程中，各作业不能中断或取消；假设7，所有作业加工的开始时间和交货时间已知；假设8，任意作业中的任意工序在某台机器上处理完转向另一台机器的时间已知。

2.2 优化目标分析

目标函数一，最小作业车间能源碳排放成本。作业车间能源碳排放是指由生产车间消耗电能所产生的碳排放成本。生产车间能耗主要包括机器正常加工能耗、怠速空转能耗、其他非调节性的固定能耗以及工件转移产生的能耗。采用排放因子法核算碳排放量，由产生碳排放的活动数据乘以对应的排放因子（以及深层次因子）来计算排放，分别如公式（1）、公式（2）所示。

Cp=EF电能×E （1）

（2）

式中：Cp为i作业的j工序在机器k加工时生产车间能耗产生的碳排放量；E、EF电能分别为生产过程中的电能消耗总量和电网平均排放因子；Tijk为i作业的j工序在机器k上的加工时间；Xijk为决策变量，当作业i的j工序在机器k上加工时Xijk=1，否则Xijk=0；Ck为机器k的完工时间；Pk和pk分别为机器k加工功率和闲置功率；S为工件转移次数；Pt工件转移功耗；Ps为加工车间的非调节性固定工率。

作业车间生产碳排放成本总和如公式（3）所示。

C1=α×Cp （3）

式中：C1为碳排放成本；α为单位碳排放成本。

碳捕捉引起的企业有形损失成本如公式（4）所示。

C2=Cp×pc （4）

式中：C2为二氧化碳治理成本；pc为每单位二氧化碳的碳捕捉价格。

中国二氧化碳捕集利用与封存（CCUS）年度报告（2023）提到电力行业碳捕集成本为200元/t～600元/t。本文取中间值400元/t来计算碳捕捉成本。

有形损失成本，即碳或有成本为碳排放税，如公式（5）所示。

C3=Cp×Tax （5）

式中：C3碳或有成本；Tax为单位二氧化碳排放的应征税额。

预防成本和鉴定成本通常由生产企业根据实际经营状况自行决定，对调度优劣不存在影响，因此将作业车间能源碳排放成本、二氧化碳治理成本和有形损失碳成本进行加总，即可得到本模型的目标函数一，作业车间二氧化碳排放成本最低，如公式（6）所示。

minf1=C1+C2+C3 （6）

目标函数二，最大作业完工时间最小。最大作业完工时间指的是从加工开始到加工完最后一个工件所花费的时间。缩短最大完工时间可以显著提高车间的生产效率，最大完工时间越短代表车间生产效率越高，如公式（7）所示。

（7）

式中：Ti为作业i的完工时间。

目标函数三，延期时间最短。延期时间是指作业工序的实际完成时间超出预定的计划时间。优化总延期时间能帮助订单式生产企业如期交货，并减少产品的囤积现象，如公式（8）所示。

（8）

式中：Li为作业i的延期时间。

目标函数四，设备负荷最小。设备总负荷是所有作业完成后参与加工的设备的总工作时间。设备利用率越高，设备总负荷就越小。设备总负荷如公式（9）所示。

（9）

约束条件分别如公式（10）～公式（13）所示。其中，公式（10）表示任意一个作业均需要经过s道完整工序才算完成；公式（11）表示任意作业的一道工序只能选定在一个机器上执行；公式（12）表示一个工序只有在前面的工序处理完成后才能开始处理下一道工序；公式（13）表示任意机器在加工任意作业过程中时不能被中断。

（10）

（11）

TSij+1-TCij≥0，i，j （12）

TSijk +Tijk =TCijk （13）

3 算法设计

3.1 编码和解码

本文采用了文献[8]提出的基于工序排序和机器选择的双层个体编码方式和贪婪解码算法。

3.2 非支配排序

随着目标函数增多，智能算法的求解效率会显著降低，寻优难度也会提升，使用Pareto支配[9]可以大幅提高算法运行效率。

3.3 基于激素调节机理的自适应因子

通常在遗传算法种群进化的前期，较大的交叉概率、较小的变异概率有利于种群快速收敛，不易丢失较优解；而在算法进化后期，会使交叉概率逐渐变小、变异概率逐渐增大，有助于搜索精细化和种群多样化。但传统遗传算法的交叉概率和变异概率是固定的，并需要自行设置，参数的选择会在一定程度上影响遗传算法的最终优化结果，但选择合适的参数值较难，因此设置自适应交叉变异概率，使种群进化过程中的交叉概率由大变小、变异概率由小变大可解决上述问题。本文将内分泌激素调节规律的上升和下降函数引入NSGA-Ⅲ算法，用于自适应调节交叉和变异概率。生物激素调节机理的上升规律函数Fup（G）、下降规律函数Fdown（G）都服从Hill函数规律，如公式（14）、公式（15）所示。

（14）

（15）

式中：G为函数自变量；D为阀值且Dgt;0；n为Hill系数且n≥1。

按照上述原理，交叉变异概率如公式（16）、公式（17）所示。

Pm=Pm0（α×Fup（G）+Sx0） （16）

Pc=Pc0（α×Fdown（G）+Sx0） （17）

式中：Pm、Pc分别为变异概率、交叉概率；Pc0、Pm0分别为初始变异、交叉概率；a为常量系数；Sx0为基础分泌常数。

上述原理能使算法迭代过程的交叉概率逐渐变小、变异概率逐渐增大，保证算法在前期快速收敛，后期不容易丢失最优解和陷入早熟。

3.4 算法流程

引入激素调节机理的改进NSGA-Ⅲ算法流程如图1所示。图中斜体部分为主要改进之处。

4 试验仿真

将基于生物激素调节机理的改进型NSGA-Ⅲ算法和其他算法进行比较，采用文献[4]中的8×8实例和文献[10]中的算例数据进行软件仿真。

车间非调节性功率为35kW，工件转移功率为2kW。本文采用的算法程序参数设置如下：初始交叉概率为0.9，初始变异概率为0.1，G为当前迭代次数，Hill常数n=1，阈值D=2，父代个体数量为100。GA和改进GA算法需要将处理的多目标问题转为单目标问题，权重设置为[0.2，1×10-7，0.01，0.1]。父代个数均为100，迭代数均为200代，每种智能算法独立试验20次，求解出的各目标平均值见表1。

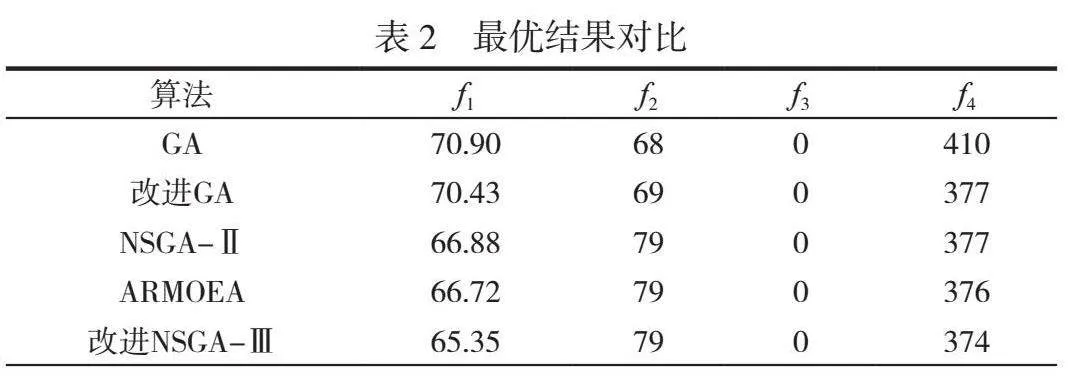
表1仿真结果显示，在同样的参数设置下，本文改进型NSGA-Ⅲ算法所得各目标函数值平均值均优于其他算法。比较每种算法的最优结果可知，在相同参数设置下，本文使用的改进型NSGA-Ⅲ算法的求解质量更优，见表2。对应最优调度甘特图如图2所示。

不难看出，设备总负载越低，设备碳成本越低，设备利用率越高，最大完工时间也会相应增加。但本文所得方案的总拖期时间仍然是0，说明本文设计的作业车间调度模型能够降低碳排放成本和能耗需求，并能保证生产正常进行，验证了本文在作业车间调度中考虑碳排放成本的可行性。

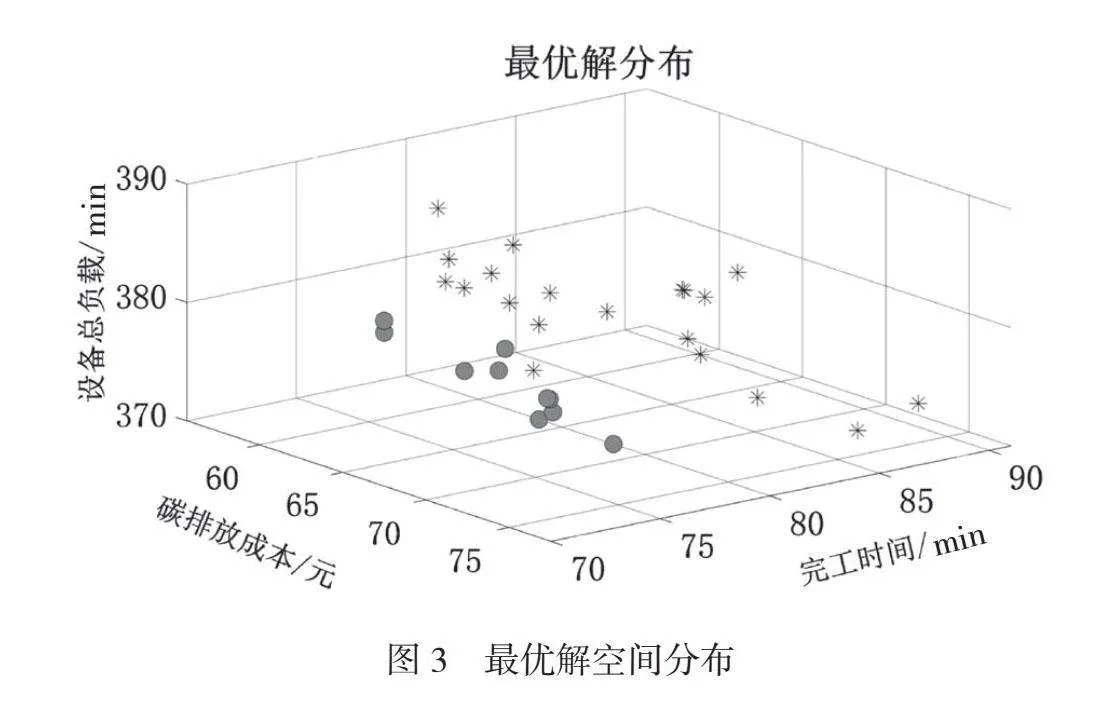
使用基于激素调节机理的自适应因子的改进型NSGA-Ⅲ算法（圆点）与其他算法（星点）的最优解空间对比如图3所示，不难看出改进型NSGA-Ⅲ算法在最优解的分布上优于传统算法。

5 结论

本文针对作业车间碳排放成本、最大完工时间、总延期时长以及设备总负荷4个目标组成的高维目标低碳柔性车间调度问题建立综合优化模型，采用基于激素调节机理的改进型NSGA-Ⅲ算法求解最优调度方案。实际生产数据的模拟仿真表明，本文的改进型NSGA-Ⅲ算法在求解质量上优于传统算法，并且所提低碳柔性车间调度优化模型可在降低碳排放成本的同时满足作业加工工序的要求。在碳成本日益凸显的当下，将其作为约束引入生产调度优化具有现实意义。

参考文献

[1]范雅男，逄焕利.求解柔性流水车间调度问题的粒子群优化算法[J].长春工业大学学报，2022（3）：258-264.

[2]WU X，SUN Y.A green scheduling algorithm for flexible job shop with Energy-Saving measures[J].Journal of cleaner production，2018，172（3）：3249-3264.

[3]LIU A，YU Y，XING Q，et al.Improved collaborative particle swarm"algorithm for job shop scheduling optimization[J].Journal of computational"amp; theoretical nanoscience，2011，4（合刊）：2180-2183.

[4]杨冬婧，雷德明.新型蛙跳算法求解总能耗约束FJSP[J].中国机械工程，2018，29（22）：2682-2689.

[5]李丹，向凤红，毛剑琳.基于INSGA-Ⅱ高维目标柔性作业车间调度的优化[J].重庆邮电大学学报（自然科学版），2022，34（2）：341-348.

[6]宋佳容，申雪峰，冯悦，等.基于改进蚁群算法的绿色柔性流水车间调度问题研究[J].辽宁工业大学学报（自然科学版），2023，43（4）：245-251.

[7]杨蓓，汪方军，黄侃.适应低碳经济的企业碳排放成本模型[J].西安交通大学学报（社会科学版），2011，31（1）：44-47.

[8]杜晓亮，张楠，孟凡云，等.改进NSGA2算法求解柔性作业车间调度问题[J].组合机床与自动化加工技术，2022（5）：182-186.

[9]操心慧，许丽娟.基于Pareto支配的高维多目标优化算法的分析与研究[J].现代计算机，2023，29（2）：62-67.

[10]王秋莲，段星皓.基于高维多目标候鸟优化算法的柔性作业车间调度[J].中国机械工程，2022，33（21）：2601-2612.