基于参数规划的含储能基电力系统低碳经济调度

摘 要：本文基于参数规划方法，研究了含储能基电力系统的低碳经济调度问题。对经济性目标和低碳目标进行权衡，建立了一个多目标优化模型。利用参数规划方法，直接求解完整的Pareto前沿，得到了一系列解决方案。通过对比分析，找到了经济性和低碳性之间的最佳平衡点。研究结果表明，参数规划方法在解决含储能基电力系统低碳经济调度问题上具有一定的优越性。

关键词：参数规划；电力系统；低碳经济调度

中图分类号：TM 74" " 文献标志码：A

随着环境保护和可持续发展的要求不断提高，低碳经济调度成为电力系统运行的重要目标之一[1]。含储能基电力系统作为一种新兴的电力系统形式，具有能量储存和灵活调度的特点，为低碳经济调度提供了新的机会。但是经济性目标和低碳目标之间的权衡关系很复杂，传统的优化方法往往无法得到全面的解决方案[2]。因此，本文采用参数规划方法，通过权衡经济性和低碳性，求解含储能基电力系统的低碳经济调度问题。

1 多目标优化算法

1.1 基于参数规划的Pareto前沿求解方法

该问题考虑了风电的不确定性、不稳定性以及储能技术引入，旨在最大程度地提高风电的利用率和经济性，同时减少碳排放，可对多目标线性优化问题进行建模。如公式（1）所示。

（1）

式中：x为要优化的决策变量；A、b为问题中的约束条件；c1、c2、c3为不同目标的权重。

在多目标优化问题中，通常希望找到一组解，这些解在多个目标函数下都是最优的。ε约束法是一种常用的方法，它通过引入ε约束来将多目标优化问题转化为单目标优化问题。具体而言，为每个目标函数引入一个ε值，将目标函数约束在一个ε范围内。通过调整ε值得到一系列解，这些解构成了Pareto前沿。而参数规划是一种特殊的优化问题，其中优化问题中的一些系数是关于一组参数的函数[3]。如公式（2）所示。

（2）

式中：c决定了目标函数的系数；B为约束条件的系数；θ在定义域Θ内取值。约束条件Bx≤θ限制了变量x的取值范围，可以保证解满足问题的实际约束。求解问题，得到相应的最优解x*（θ）和最优值v*（θ）。通过改变θ的值来研究问题的不同方面，了解不同情况下的最优解和最优值。

关键区域是参数空间Θ的一个子集，它由一组特定的约束条件定义[4]。基于ε约束法如公式（3）所示。

（3）

式中：ε2、ε3被视为问题的参数，它们的取值影响问题的最优解和最优值，其参数空间如公式（4）所示。

Θ={（ε2，ε3）|ε21≤ε2≤ε2u，ε31≤ε3≤ε3u} （4）

式中：ε3u为ε3的上界，即ε3的取值不能超过ε3u；ε3l为ε3的下界，即ε3的取值不能小于ε3l。将ε3的取值限制在ε3l和ε3u之间。

当（ε2，ε3）∈Θ时，最优解x*满足公式（5）。

c2Tx*= ε2

c3Tx*=ε3 （5）

根据定义，如果一个解在目标函数空间中无法被其他解支配，那么它就位于Pareto前沿上。因此，（v1，ε2，ε3）是Pareto前沿上的一个点。在每个关键区域内，通过线性组合参数θ的线性函数表示最优值v*。每个超平面都对应参数空间内的一个关键区域。这些超平面表示了在不同参数取值下的最优解，并且它们之间形成了Pareto前沿。不同的参数取值会导致不同的超平面，从而产生不同的最优解[5]。通过探索参数空间中的不同区域，获得Pareto前沿上的多个最优解。

1.2 基于工程博弈的多目标优化方法

Nash协商博弈法是一种博弈论中的解决方案，它利用协商和合作的方式来找到参与者之间的均衡点。每个主体都有自己的成本函数，并且希望通过协商和合作来达到最小化自身成本的目标。将多目标优化问题视为一个谈判博弈，其中有3个虚拟参与者。每个虚拟参与者的谈判目标是最小化各自的成本函数，通过博弈和协商的方式来达成一致并找到一个均衡点。这个均衡点对应多目标优化问题的最优解。如公式（6）所示。

（6）

采用参数规划算法求解多目标优化问题。参数规划算法是一种基于参数空间搜索的优化方法，它通过调整参数的取值来寻找最优解，如公式（7）所示。

v1=p1v2+qiv3+ri，（v2，v3）∈CRi " " " " " " " （7）

通过计算得到关键区域内v1关于（v2，v3）的解析表达式。这些解析表达式描述了在每个关键区域内，v1与其他目标变量v2和v3之间的关系。

在多目标优化问题中，将每个关键区域CRi视为一个工程博弈问题。工程博弈是一种博弈论中的解决方案，它将决策问题视为多个参与者之间的博弈问题，如公式（8）所示。

（8）

检查是否满足piqi≠0且（* 2，* 3）∈的条件。若满足，则（* 2，* 3）为最优解。

如果不满足上述条件，就说明在CRi的边界上取得最优解。在这种情况下，需要将为为关于的仿射函数。利用这个仿射函数，将问题转化为一个单目标优化问题。解决这个单目标优化问题，找到（* 2，* 3）的最优解。这个最优解对应在CRi的边界上的最优决策点。其计算过程如公式（9）所示。

（9）

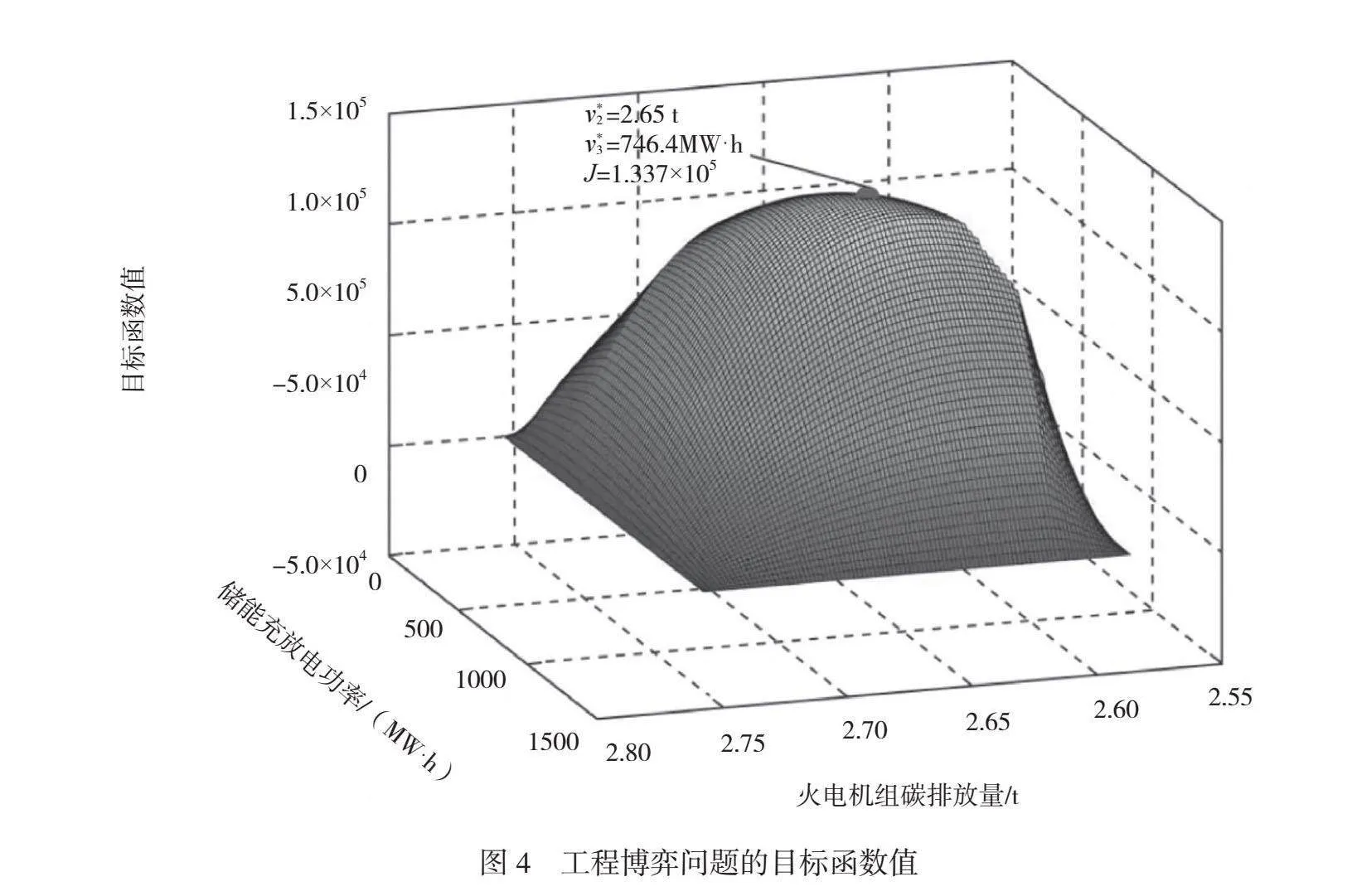
计算每个关键区域CRi对应的工程博弈问题的最优值Ji。这些最优值描述了在每个关键区域内的最优决策方案。从这些最优值中找出最大的最优值J*，并确定其对应的目标值（v* 1，v* 2，v* 3）。这个目标值即为最终的决策点，它表示在多目标优化问题中的最优解。

2 算例分析

2.1 算例介绍

为了优化能源系统的运行和资源利用，须对这个问题进行建模。线性规划问题是一种数学优化问题，目标是在给定的约束条件下，最大化或最小化线性目标函数。采用商业求解器CPLEX求解这个线性规划问题。CPLEX是一种高效的数学规划求解器，它通过线性规划算法来找到最优解。将能源系统的运行约束和目标函数转化为线性形式，使用CPLEX对该线性规划问题进行求解。CPLEX将根据给定的约束条件和目标函数，利用优化算法找到能使目标函数最大化或最小化的最优解。5节点系统的拓扑结构示意如图1所示，该系统包括4台火电机组（G1、G2、G3、G4）、1座风电场（W1）、2个储能系统（E1、E2）、3个分配器（D1、D2、D3）。

2.2 结果分析

minv1是指在多目标优化问题中，最小化目标函数v1的值。v1为系统的某种性能指标或者成本指标。通过最小化v1，追求系统的高效性、性能提升或者成本降低。minv2是指在多目标优化问题中，最小化目标函数v2的值。v2为系统的另一个性能指标或者其他重要的指标。通过最小化v2，追求系统其他个方面优化，例如安全性、可靠性或者可持续性。minv3是指在多目标优化问题中，最小化目标函数v3的值。v3为系统的另一个性能指标或者其他关键的指标。通过最小化v3，追求系统其他方面优化，例如环境友好性、资源利用率或者用户满意度。这3个目标函数（minv1、minv2、minv3）共同构成了多目标优化问题的目标函数集合。见表1。关键区域划分结果如图2所示。

通过运用优化算法和约束条件，找到一个最优解决方案，使系统在各个目标函数上都能够达到最大化。最终选择决策点使各目标函数值都能够达到最大化，在整个系统中同时实现经济性、环保性和储能寿命等多个目标。这种综合考虑各个目标的方法可以帮助决策者做出更全面、更合理的决策，优化系统的整体效益，并在不同目标之间取得平衡。Pareto前沿和目标函数如图3、图4所示。

储能技术可以将多余的风电能量储存起来，需要时释放出来供电。通过调度和控制储能系统，平衡风电的不稳定性，使风电发电量能够更好地满足负荷需求。因此，在含储能的情况下，风电发电量增加，能够更充分地利用风能资源，提高风电的发电量和利用率。火电发电量在含储能的情况下有所减少。由于引入了储能系统，系统能更好地调度和管理电力供应，使风电能够更多地满足负荷需求，减少对传统火电的依赖。因此，在含储能的情况下，火电发电量减少，从而减少了化石燃料的消耗和碳排放。这个结果说明新能源与储能接入可以使发电更经济和环保。通过引入储能技术，系统能够更好地利用可再生能源，提高新能源的消纳能力和利用效率。同时，运用储能技术也能提高电力系统的灵活性和可靠性，减少对传统火电的依赖，从而减少碳排放和环境污染。火电机组和风电场各时段的出力如图5所示。

2.3 与传统方法对比

本文考虑了经济性目标v1和低碳目标v2。传统方法采用采样法生成一系列解，对这些解进行加权求和，得到一个最优解。由于采样法得到的点分布不均匀，因此得到的最优解并不能很好地反映真实的Pareto前沿。相比之下，加权法更好地兼顾不同目标之间的权衡关系。通过调整不同目标的权重，得到一系列不同的最优解，这些解构成了Pareto前沿的近似。加权法能够更准确地探索目标函数之间的权衡关系，找到更优的解决方案。利用加权法，在经济性目标v1和低碳目标v2之间找到一个合理的平衡点，加权法的处理方式如下。

本文选取了101个不同的λ取值，分别为0.1、0.2、…、10。将这些λ值应用于归一化后的v1和v2，得到了101组点（v01，v02）、（v11，v12）、…、（v1100，v2100）。这些点表示了在不同的低碳目标权重比下，经济性目标v1和低碳目标v2的组合。每个点都表示一个解决方案，它们在经济性和低碳性之间的权衡关系不同。通过改变λ的取值，探索不同的目标权重比对解决方案的影响。通过分析这101组点，得到一个完整的解决方案集合，每个解决方案都在不同程度上满足经济性和低碳性的要求。通过比较这些解决方案，找到最优的解决方案，即在特定的目标权重比下，能够同时实现经济性和低碳性的最佳平衡点。加权法得到的Pareto点分布如图6所示。

参数规划方法是通过调整参数的取值来得到一系列的解决方案，这些解决方案构成了Pareto前沿的近似。通过这种方法，可以更全面地探索目标函数之间的权衡关系，找到更优的解决方案。使用参数规划方法，直接得到Pareto前沿上的点，而不需要利用采样法得到的点，避免采样法带来的分布不均匀和拟合效果较差的问题。参数规划方法可以更准确地探索目标函数之间的权衡关系，找到更优的解决方案，并且不需要反复调整权重λ的取值，节省了时间和精力。

3 结语

本文通过对比分析，找到了经济性和低碳性之间的最佳平衡点，为电力系统的可持续发展提供了参考。未来的研究会进一步探索其他优化方法和调度策略，以提高含储能基电力系统的低碳经济调度效果。

参考文献

[1] 陈行滨，邹墨，李霄铭，等.电力系统负荷数据预测的设计与实现[J].微型电脑应用，2022（7）：38.

[2] 王云会，郑强仁，郭淼，等.配电网中广义虚拟电厂的柔性优化规划问题研究[J].供用电，2022，39（3）：8.

[3] 李寒，张成宇，王同勋，等.基于电力大数据的谐波仿真系统[J]. 计算机系统应用，2019，28（8）：87-94.

[4] 崔宏斌.电力规划设计在电力工程设计中的应用[J].中国厨卫， 2022（2）：3.

[5] 李固.基于光伏发电工程的电力系统长期规划模型研究[J].现代工业经济和信息化，2023，13（8）：192-194.