立式高速数控机床热变形误差超前预测方法

摘 要：由于使用现有预测方法进行预测的预测结果与温度实际值的残差最大值＞0.03 μm，预测效果差，因此本文研究立式高速数控机床热变形误差超前预测方法。利用卷积神经网络将温度场映射至热误差的预测空间中，使热变形数据作为热误差预测模型的输入，还原温度场。建立数控机床热误差预测模型，将测温点的温度数据代入模型中，可以预测热误差。设计分布差异的更新方法，将阈值设为作用范围有限圆半径的值，当预测样本点至预测结果的距离等于该阈值时，系统输出相应的预测结果。试验结果表明，试验组的关键测温点的温度预测曲线与温度实际值比较一致，在8个测温点中计算得到的残差最大值均为0.01 μm～0.03 μm，结果符合预期。本文方法能够保证预测值与实际值之间偏差较小，提升预测模型的稳定性。

关键词：高速；数控机床；热变形；误差；超前预测

中图分类号：TP 273" " " " 文献标志码：A

在机床高速运转过程中，由于内部热源和外部环境温度的影响，机床结构会产生热变形，因此产生加工误差。为满足现代制造业的需求，须实时监测机床关键部位的温度变化，结合历史数据和机器学习算法构建准确的预测模型。该模型不仅能够实时反应机床的热变形状态，还能够基于当前状态和历史趋势对未来的误差变化进行超前预测。使用该模型可以提前了解机床热变形误差的变化趋势，为机床的调整和维护提供科学依据。布置足够的测量点，全面反映机床的热变形情况，提高机床的加工速率和生产效率。由于文献[1]接触式测量技术需要在机床的关键部位安装传感器来获取热变形数据，因此可能出现测量误差，对机床的正常工作产生干扰，损坏测量装置。文献[2]在机床的关键部位安装千分表，通过接触来检测机床的热变形情况。由于需要直接与被测物体接触，因此可能会对机床的正常工作造成干扰，甚至可能损坏测量工具或机床表面。机械式测量工具的读数容易受到人为因素影响，可能导致测量误差。综上所述，现阶段采用立式高速数控机床热变形误差超前预测方法作为研究对象，结合实际情况进行试验和分析。

1 热变形误差超前预测

1.1 卷积神经网络输入处理

在对立式高速数控机床进行热误差实时预测的过程中，需要利用卷积神经网络将温度场映射至热误差的预测空间中[3]。在该过程中，需要将温度场作为模型的输入，将热误差作为模型的输出，得到预测结果。

因此，在建模前必须对输入的温度数据进行适当处理。运用卷积神经网络的输入层进行数控机床热变形数据处理，将温度数据按照通道节点的顺序排列为一维向量，将其转换为矩阵形式，作为热变形图像数据输入。在转换过程中，无法填充的部分会用0进行填充。将所有温度信息输入模型，获得温度测点中全部机床结构信息，提升预测模型的精度，。在实际过程中，根据测温点布置，构造1个单通道二维矩阵图像，用于存储温度信息以及机床结构信息。构建1个M×N的温度图像，将测温点的机床结构区域映射至该图像中。设定区域内的像素点集合为k，存在的像素点为1，不存在的像素点为0。图像中的每个像素值都反映机床的特定温度信息[4]。在输入过程中，设置任意时刻的温度场矩阵Aij来反映任意时刻的温度值，如公式（1）所示。

Aij={（aijcij）t} " " " " （1）

式中：aij为矩阵中的元素值；cij为元素对应的温度值；t为温度场矩阵中的某个时刻。利用热成像图像获取热变形数据，将热变形数据用于热误差预测模型的输入，使用热成像图像等转换数据来还原温度场，保存整个温度场信息。将温度场中的数据映射至热误差的预测空间中，完成模型的输入。

1.2 BP神经网络热误差超前预测建模

1.2.1 数据标准化处理

在加工过程中，数控机床需要对热误差进行实时测量，基于数控机床在加工过程中温度数据与热误差之间的映射关系，利用温度数据预测热误差。对优化后的BP神经网络进行训练，建立数控机床热误差预测模型[5]。利用温度和热误差数据样本对网络进行迭代学习，在模型中建立非线性连接，将加工数据作为训练样本集，采用归一化方法对温度与热误差数据进行标准化处理，还原热误差值。其计算过程如公式（2）所示。

（2）

式中：i为元素数量；max（x）、min（x）为矩阵中的最值。

1.2.2 BP神经网络结构设计

BP神经网络的结构设计在构建预测模型中作用十分重要。1个精心设计的神经网络结构能够提取数据中的特征，准确地映射输入与输出之间的关系。

输入层是神经网络的第一层，其负责接收原始数据。在热误差预测模型中，输入层节点数与温度数据的维度相同。说明每个测温点都将对应1个输入节点，保证神经网络能够全面捕捉温度数据的变化。

隐藏层是神经网络的核心部分，其利用多层非线性变换来提取数据的复杂特征。隐藏层的层数和节点数对神经网络的性能有重要影响。隐藏层和节点数过多可能导致网络过于复杂，容易出现过拟合现象；层数和节点数过少可能无法充分捕捉数据的非线性关系，导致预测精度下降。

因此，当设计隐藏层时，需要根据具体任务和数据集的特点进行权衡。一种常用的方法是利用试验来逐步增加隐藏层的层数和节点数，观察网络在验证集中的性能变化。当性能开始下降或出现过拟合现象时，可以认为当前的网络结构已经足够复杂，无须再增加隐藏层和节点数。

输出层是神经网络的最后一层，其作用为输出预测结果。在热误差预测模型中，输出层只有1个节点，即预测的热误差值。这个节点将接收来自隐藏层的输出，并运用线性变换和激活函数得到最终的预测结果。

激活函数是神经网络中的非线性元素，其作用是使神经网络能够学习复杂的非线性关系。在BP神经网络中，常用的激活函数包括Sigmoid函数、ReLU函数等。

损失函数的作用是衡量预测值与真实值之间的差距，是神经网络的优化目标。在热误差预测模型中，常用的损失函数包括均方误差（Mean-Square Error，MSE）和交叉熵等。这些函数能够反映预测误差的大小，指导神经网络的优化方向。

1.2.3 神经网络训练与优化输出

对处理后的数据进行样本输入，运用BP神经对目标进行训练，计算输出值与预期值之间的方差。设定训练次数为300，将数据个体代入BP神经网络的每层节点中，优化权值与参数设定，进行反复迭代训练，直至训练结束。

在BP神经网络的训练过程中，采用梯度下降算法进行权重更新，如公式（3）所示。

（3）

式中：wijk为第k层第i个节点与第k+1层第j个节点之间的连接权重；λ为学习率，其作用是控制权重更新的步长；E为损失函数，其作用是衡量预测值与真实值之间的差距；为损失函数对权重wk ij的偏导数，衡量权重对损失函数的影响程度。

λ是1个重要的超参数，其大小直接影响模型的训练速度和效果。学习率过大可能导致训练过程不稳定，甚至无法收敛；学习率过小可能导致训练过程过于缓慢。因此，需要根据需求具体设置合适的学习率。

经过训练后保存网络权值，得到BP神经网络热误差预测模型，如公式（4）所示[6]。

Y=∑w[sig（wx-b）]-b' " （4）

式中：Y为热误差预测结果；w为不同层节点之间的连接权重；b为输入节点的阈值；b'为输出节点的阈值。将测温点的温度数据代入模型中，可以对热误差进行预测。

1.3 热误差预测输出

在预测过程中，样本数据在模型中存在分布差异，导致数据偏差，不同类别数据在局部区域杂乱分布，发生预测错误等问题。为解决这个问题，本文设计分布差异的更新方法。对更新的权值样本进行不断迭代，使数据分布自适应[7]。设定一个阈值K，在每轮预测过程中不断迭代预测样本的作用值。当某个样本的作用值低于该阈值K时，该样本将被删除。其预测结果如公式（5）所示。

（5）

式中：S为预测结果；sj-1 xi为在j-1训练次数条件下点xi的预测结果；j为训练次数；dist（x，xi）为点与之间的距离；Rmin为预测样本距离预测结果的最小距离。

在预测过程中，以预测样本点为中心界定1个区域，其是由多个预测样本点组成的，以展示最有效的作用范围。在计算过程中，只有与预测样本点属于同一个类别的数据才会判定为作用值并进行计算[8]。将阈值设为作用范围有限圆半径，作用域内的同类别样本的作用值会保存，作用域外的会消除。因此，当某个预测特征在空间中的某个位置重复出现时，该位置的样本点会偏离真实预测结果的数据；当预测样本点的距离小于Rmin时，删除预测结果；当预测样本点的距离等于Rmin时，说明该位置样本点与真实预测结果相等，能够准确输出预测结果，有效地消除偏差数据的干扰。在实际应用中，热误差预测输出可以应用于各种加工场景，最大程度地减少预测偏差，使模型稳定性更强。预测输出能够帮助工作人员提前了解预期误差，优化机床布局，减少热误差对加工的影响，进行超前预测。

2 试验测试与分析

2.1 搭建试验环境

在试验准备阶段，根据网络结构设置参数，对不同测温点中的数据进行处理，使其能够满足在网络训练过程中输入样本与预期输出样本需求。预测模型的参数设置见表1。

设定适当的网络层数，考虑温度数据的时间序列特性，选择一定的网络层数来获得数据中的长期依赖关系。为保证网络的训练效率，设置网络同步时间为50步，使用历史温度数据来预测未来机床温度数据变化。根据试验数据调整学习率，避免产生过拟合问题。将测温点的温度数据作为训练样本，构建温度超前预测模型。将预测得到的温度数据作为输入变量，输入至模型中进行热误差的超前预测。

2.2 结果与分析

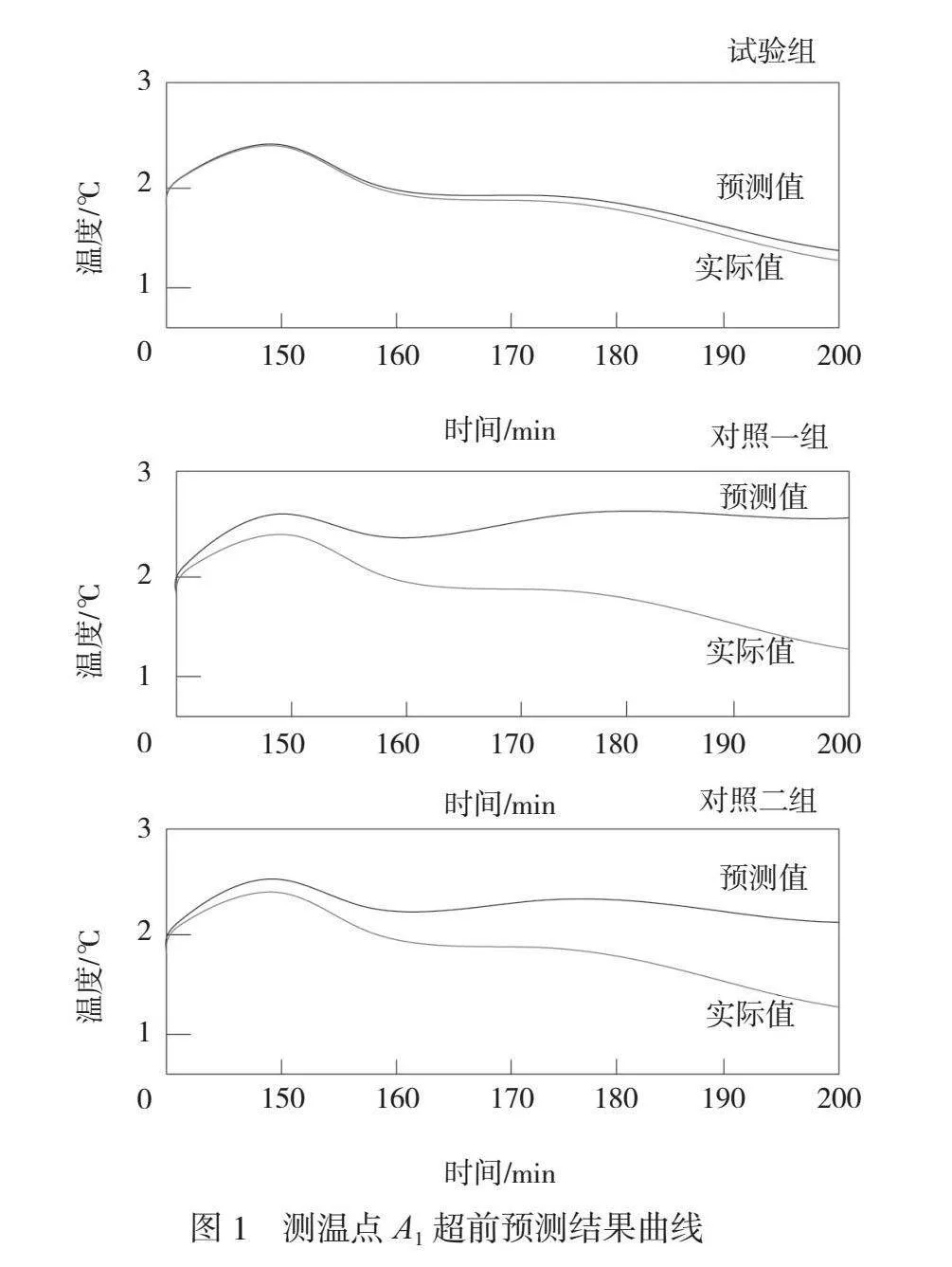
运用立式高速数控抛光机床进行试验，按照模拟过程布置测温点。选择测温点A1，使用不同方法进行温度超前预测。根据实际温度值与预测值的曲线趋势变化情况分析不同预测方法的具体效果。测温点A1超前预测结果曲线如图1所示。

由图1可知，经过测温点A1温度超前预测，将不同测温点中的温度数据输入至模型中，对比3个小组的预测结果与温度实际值，试验组的关键测温点的温度预测曲线与温度实际值比较一致，说明本文预测方法对温度变化的捕捉能力准确。本文方法在处理时间序列数据方面性能出色，能够有效地利用历史温度信息来预测未来温度变化趋势。

采用立式高速数控机床在加工过程中得到的热误差数据样本作为训练。每次机床模拟加工持续一段时间，需要对机床的热误差进行同步采样，累计时间为200 min，即样本集的总采样点数为1 800个。针对各个测温点A1～A8进行残差值计算，统计残差最大值，统计结果见表2。

由表2可知，运用本文预测方法在8个测温点中计算得到的残差最大值均为0.01 μm～0.03 μm，结果符合预期要求。说明运用本文方法进行预测后，能够保证预测值与实际值之间的偏差较小，提升预测模型的稳定性。

综上所述，本文预测模型能够根据历史温度数据对温度进行精准预测，为立式高速数控机床的热变形误差控制提供了有力支持。本文优化模型结构，提高预测精度，能够满足更多复杂场景中的温度预测需求。针对各个测温点进行残差值计算，使各个测温点的残差最大值均保持在较低水平，提升了热误差预测模型的有效性，立式高速数控机床热变形误差超前预测方法应用良好。

3 结语

本文从误差预测入手，深入分析立式高速数控机床热变形等相关问题，研究立式高速数控机床热变形误差超前预测方法。本文构建精准的预测模型，结合实时温度监测数据，对机床热变形误差进行超前预测，采取相应的补偿措施保证机床的加工精度。本文方法存在一些不足，例如产品质量问题、训练样本数量问题和机床精度问题等。未来会优化计算过程，引入先进的传感器技术，基于历史数据和实时状态对误差趋势进行超前预测。本研究为机床精确加工提供支持，能够适应更加复杂、多变的机床运行环境。

参考文献

[1]于博，王利涛，陈志红，等.数控机床热变形误差超前预测研究[J].机床与液压，2023，51（4）：75-79.

[2]杨秀芝，查吉利，徐绍勇，等.BF-850B立式高速数控机床精度检测及误差补偿研究[J].机床与液压，2022，50（22）：80-83.

[3]陶浩浩，陈丰，李同杰，等.一种基于新灵敏度指标的五轴数控机床关键几何误差辨识方法[J].仪器仪表学报，2022，43（12）：120-128.

[4]李淋，蔡站文，杨勇，等.数控插齿机热误差模块化稳健性预测模型建立[J].机床与液压，2022，50（8）：26-30.

[5]卢成伟，钱博增，王慧敏，等.工件分特征下的五轴数控机床关键几何误差分析与补偿方法[J].中国机械工程，2022，33（14）：1646-1653.

[6]刘阔，宋磊，陈虎，等.机理驱动的数控机床进给轴时变误差建模和补偿方法[J].机械工程学报，2022，58（3）：251-258.

[7]曹利，彭骥，殷鸣，等.基于MEA-BP算法的卧式加工中心主轴热误差建模[J].组合机床与自动化加工技术，2022（7）：30-33，37.

[8]杜柳青，李祥，余永维.基于自适应深度学习的数控机床运行状态预测方法[J].农业机械学报，2022，53（1）：451-458.