基于扰动观测器的时滞系统可靠输出控制分析
2024-12-05高来鑫李玲纯







摘 要:针对一类具有外部扰动和不确定性的时滞系统,在考虑到执行器故障和系统状态不可知的情况下,构造了基于输出反馈的扰动观测器和扰动补偿控制器。随后通过Lyapunov第二法判断系统稳定性,以线性矩阵不等式的形式给出系统渐近稳定的充分条件,同时运用费舍尔引理来处理控制器综合的耦合问题。最后通过数值仿真实验,验证了基于扰动观测器的控制方法对扰动抑制的有效性,并通过对比,当系统存在执行器故障时,容错控制方法比没有考虑执行器故障的控制算法对维持系统稳定、提高系统性能更加有效。
关键词:扰动观测器;时滞系统;Markov系统;线性矩阵不等式
中图分类号:TP273"" 文献标识码:A"" 文章编号:1673-1794(2024)05-0001-04
作者简介:高来鑫,滁州学院机械与电气工程学院讲师,硕士,研究方向:创新创业理论与实践、复杂性系统建模;李玲纯,滁州学院机械与电气工程学院教师(安徽 滁州 239000)。
1 引言
在实际应用中,系统不可避免地会出现时滞的现象,例如在神经网络、人口动态模型和船舶稳定分析以及电力系统,会导致系统的性能下降甚至失稳。因此对于时滞系统稳定性的分析得到了广泛关注和研究[1-4],同时也提出了很多有效并且得到应用的方法。文献[1]中对不确定性的线性时滞系统进行了鲁棒稳定性分析。文献[2]针对变时延和变结构不确定性时滞依赖系统进行了鲁棒稳定性分析工作。文献[3]中对于混合时延和变结构不确定性神经网络系统设计了鲁棒控制器。文献[4]运用滑模控制技术对于具有非线性参数扰动的不确定性线性时滞系统进行稳定性分析。文献[5]分析了有界不确定性的变时延系统的鲁棒控制。文献[6]提出采用自适应神经网络控制方法处理具不确定性的多输入多输出非线性变时延系统。本研究主要是把时滞作为一般不确定性来处理,具有一定的保守性。
基于扰动观测器的控制技术,将扰动估计引入控制律中,从而在反馈通道中对于实际扰动进行补偿。同时,无需安装额外的传感器,可以非常方便地应用于控制系统中。
2 问题描述
考虑具有不确定性和存在外界扰动的时滞系统模型如(1)所示:
x(t)·=[A+ΔA(t)]x(t)+"" [Ad+ΔAd(t)]x(t-τ(t))+"" B(u(t)+d(t))x(t)=φ(t),t∈-τM(t),0y=Cx(t)(1)
其中x(t)∈Rn是系统状态变量;u(t)∈Rm是控制输入;d∈Rm是外部扰动输入;A∈Rn×n,B∈Rn×m,Ad∈Rn×n分别为具有合适维度的系统矩阵;C是输出矩阵,y是输出量。φ(t)系统状态的初始化函数。
假设1: τ(t)满足条件如下:
0≤τ(t)≤τM(t)且τ·(t)≤h;
假设2: 系统不确定性满足条件如下:
ΔA(t) ΔAd(t)=DF(t)E1 E2
;
其中E1,E2是常数矩阵,用于表示系统结构不确定性。F(t)是未知的真实存在的变时延矩阵,满足F(t)ΤF(t)≤I,t。
假设3:矩阵B满秩,即rank(B)=m。
为了证明给出的渐近稳定的充分条件,应用的引理如下所示:
引理1 对于任意常数αgt;0,以下不等式成立:
XΤY+YΤX≤αXΤX+α-1YΤY
引理2 假设存在P=PΤ∈Rn×n和B∈Rm×n,以下命题等价成立:
(a)vΤPvlt;0,v≠0,Hv=0
(b)HΤPHlt;0;
(c)S∈Rn×m,使P+He(SH)lt;0
引理3 假设给定对称矩阵S=S11S12ST12S22,S11∈Rr×r,以下三个命题等价:
(a)Slt;0
(b)S11lt;0,S22-SΤ12S-111S12lt;0
(c)S22lt;0,S11-S12S-122SΤ12lt;0
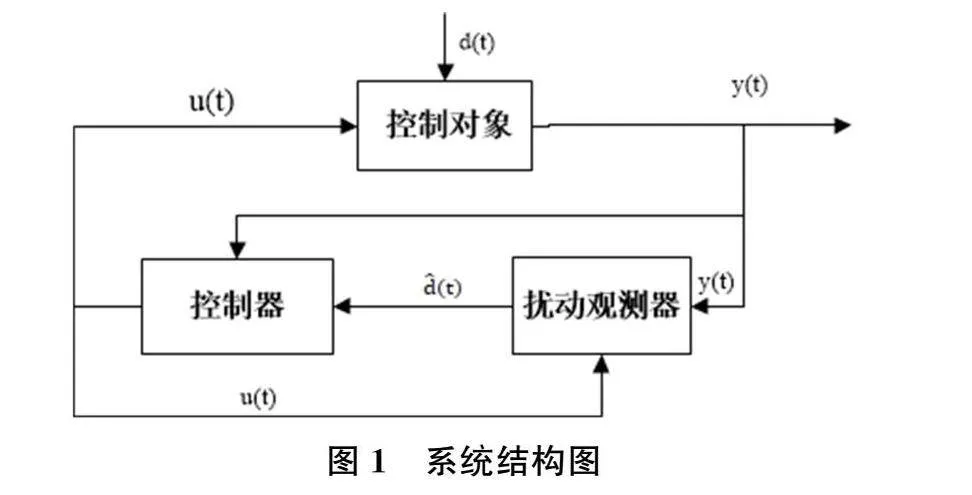
基于DOB技术时滞系统输出反馈控制结构图如图1所示:
现有参考文献中关于控制器的设计多数是基于状态反馈,然而在现实工业系统中,系统状态或者状态的估计可能不可知。文章提出通过输出反馈控制和利用时滞依赖的方法来处理这一类不确定时滞系统。假设系统状态不可知,依靠系统输出构造扰动观测器和控制器。
3 系统结构设计
3.1 扰动观测器构造
系统常见外部扰动表示如下(2)式:
ω·(t)=Wω(t)d(t)=Vω(t)(2)
其中ω(t)∈Rn,d∈Rm,可以描述一系列系统外部产生的常见扰动。当W=0,V=1时候可以表示未知数值的常值负载扰动。满足以下条件(3)可以描述已知频率ω,未知幅值和相位的谐波扰动。
W=0ω-ω0,V=10(3)
针对上述扰动结构,构造如下扰动观测器结构(4):
d︿=Vω︿(t)ω︿(t)=v(t)-Ly(t)v·(t)=(W+LCBV)ω︿(t)+LCBu(t)(4)
其中L∈Rn×n是扰动观测器的增益,d︿是扰动估计,v(t)是扰动观测器内部状态。
注1:对于上诉扰动观测器结构,对观测器内部状态表达式进行求导,可得如下表达式:
ω︿(t)=(W+LCBV)ω︿(t)+LCBu(t)-Ly·(t)(5)
通过(5)式可以得出,基于输出反馈的扰动观测器只要获取系统的控制律u(t),系统输出y(t)以及系统输出的导数y·(t)。对于状态不可知的实际工业系统,具有很好的应用价值。
3.2 输出反馈控制器构造
基于扰动观测器(4),假设系统状态不可知,设计如下的输出反馈控制器(6)
u(t)=Ky(t)-d︿(t)(6)
控制率由系统输出的线性表达和扰动估计的补偿组成。其中K是输出反馈控制器增益。
同时考虑到执行器故障,相应的系统结构可以如下(7)表示:
x·(t)=[A+ΔA(t)]x(t)+[Ad+ΔAd(t)]x(t-τ(t))+BI-ρ(u(t)+d(t))(7)
参数ρ=diag(ρ1,ρ2,……ρm)满足如下约束:
0≤ρ-k≤ρk≤ρk,"" k=1,2,……,m
其中ρk(k=1,2,……,m)表示执行器失效参数,假设ρk的上界和下届都是已知的常数,同时定义
ρ-=diag(ρ-1,ρ-2,……ρ-m),ρ=diag(ρ1,ρ2,……ρm)
可以得出以下表达式:
Nρ={ρ:ρ=diag(ρ1,ρ2,……ρm)," ρk=ρ-k" or"" ρk,nbsp; k=1,2,……m},Nρ最多包含2m个元素。
对于具有外界扰动的时滞系统,可以通过设计HSymboleB@控制器进行扰动抑制,但是对扰动的形式没有提出具体结构,扰动抑制的结果则具有保守性。研究对于扰动提出了具体扰动的结构,保守性得到降低。
3.3 扰动估计误差
设e(t)=ω(t)-ω︿(t),定义为扰动估计误差,对其求导,结合(1)(2)(4)(6)可以得到以下表达式(8):
e·(t)=ω·(t)-ω︿·(t)=Wω(t)-(v·(t)-Ly·(t))"""""" =(W+LCB(I-ρ)V)e(t)+LC(A+ΔA)x(t)"""""" +LC(Ad+ΔAd)x(t-τ)-LCBρKCx(t)
(8)
注2:由上式可知,为使扰动估计值趋近于真实值,e(t)必须收敛。当控制器实现状态量镇定控制时,x(t)→0,x(t-τ(t))→0,当存在合适的L使得W+LCB(I-ρ)Vlt;0,则(8)实现了关于e(t)的指数稳定。因此扰动观测器增益L对于扰动观测器性能起到非常重要的作用。由上面两部分分析可知,求解出合适的扰动观测器增益L矩阵参数和控制器增益K参数可以使得闭环系统状态和扰动估计误差e(t)都稳定。
结合(7)和(8)可以给出系统复合结构(9):
ζ·(t)=Aξ(t)+Adx(t-τ)ξ(t)=xT(t)eT(t)T (9)
A="""""""""""""""""" A+ΔA+B(I-ρ)KCB(I-ρ)VLC(A+ΔA)-LCBρKCW+LCB(I-ρ)V
Ad=Ad+ΔAdLC(Ad+ΔAd)
4 主要结果
4.1 稳定性分析
如下给出了系统渐近稳定的充分条件。
定理4.1:如果存在正常数αi," i∈(1,2,3,4)和正定矩阵P1∈Rn×n,P2∈Rn×n,R∈Rn×n以及矩阵Q1∈Rn×n,Q2∈Rn×n,Q3∈Rn×n,Q4∈Rn×n使得如下的不等式(10)成立:
Γ=Γ11Γ12Γ13Γ14*Γ22Γ23Γ24**Γ33Γ34***Γ44≤0(10)
其中:
Γ11=He(P1(A+B(I-ρ)KC))+(α1+α2)PDDΤP+(α-11+α-13)EΤ1E1+P1-Q1-QΤ1Γ12=P1B(I-ρ)V+(P2LCA-P2LCBρKC)Τ-Q4Γ13=P1Ad-Q2+QΤ1Γ14=QΤ1-Q3Γ22=He(P2(W+LCB(I-ρ)V))+(α3+α4)P2LCDDΤCΤLΤP2Γ23=P2LCAd+QΤ4Γ24=QΤ4Γ33=(α-12+α-14)EΤ2E2+(τ·-1)R+QΤ2+Q2Γ34=QΤ2+Q3Γ44=QΤ3+Q3
则系统状态和扰动观测器状态都渐近稳定。
证明:选取李雅普诺夫泛函如下:
V(t)=ξT(t)P100P2ξ(t)+∫tt-τxT(s)Rx(s)ds(11)
同时P应满足Pgt;0并且设P=P100P2,其中P1gt; 0, P2gt; 0。
把控制律(6)代入考虑到执行器故障系统状态中(7),可以得出如下系统表达式(12)
x·=(A+ΔA)x+(Ad+ΔAd)x(t-τ)+
B(I-ρ)(Ky(t)-d︿+d)" =(A+ΔA)x+(Ad+ΔAd)x(t-τ)+
B(I-ρ)(KCx(t)-d︿+d)" =(A+ΔA+B(I-ρ)KC)x+
(Ad+ΔAd)x(t-τ)+B(I-ρ)(d-d︿)(12)
结合(8)(12)和牛顿莱布尼茨公式对所取的李雅普诺夫泛函(11)式进行求导可得(13):
V·=2x(t)ΤP1x·(t)+2eΤ(t)P2e·(t)+
xT(t)Rx(t)+(τ-1)xΤ(t-τ)Rx(t-τ)+2[∫tt-τx·(s)ds-x(t)+
x(t-τ)]Τ[Q1x(t)+Q2x(t-τ)+∫tt-τx·(s)Q3ds+Q4e(t)](13)
为了处理由x·(t)和e·(t)所产生的非线性部分,通过引理1对于非线性部分进行缩放可得如下不等式:
2xT(t)P1DF(t)E2x(t-τ)≤
α2xTP1DDTP1x(t)+α-12x(t-τ)T·
ET2E2x(t-τ)2eTP2LCDF(t)E1x≤
α3eTP2LCDDTCTLTP2e(t)+
α-13xT(t)ET1E1x(t)
2eTP2LCDF(t)E2x(t-τ)≤
α4eTP2LCDDTCTLTP2e+α-14x(t-τ)TET2E2x(t-τ)
不等式和(13)可以得到(14):
V·≤2x(t)TP1(A+B(I-ρ)KC)x(t)+α1xT(t)P1DDTP1x(t)+α-11xT(t)ET1E1x(t) +2xT(t)P1Adx(t-τ)+α2xT(t)P1DDTP1x(t)+α-12x(t-τ)TET2E2x(t-τ)+2xT(t)P1B(I-ρ)Ve(t)+xT(t)Rx(t)+xTP1x+(τ·-1)x(t-τ)TRx(t-τ)+2eT(t)P2(W+LCB(I-ρ)V)e(t)+2eT(t)P2(LCA-LCBρKC)x(t)+2eT(t)P2LCAdx(t-τ)+α3eT(t)P2LCDDTCTLTP2e(t)+α-13xT(t)ET1E1x(t)+
α4eT(t)P2LCDDTCTLTP2e(t)
+
α-14x(t-τ)TET2E2x(t-τ) +2[∫tt-τx·(s)ds-x(t)+x(t-τ)]T×[Q1x(t)+Q2x(t-τ)+Q3∫tt-τx·(s)ds+Q4e(t)](14)
式(14)等价于如下状态空间表达式:
V·≤x(t)e(t)x(t-τ)∫tt-τx(s)ds·TΓx(t)e(t)x(t-τ)∫tt-τx(s)ds·
为了保证系统的稳定性,只需要满足v(t)lt;0,整理上述空间表达式,可得Γ在定理4.1中的不等式,证明完毕。
4.2 控制器和扰动观测器综合
定理4.1给出了系统渐进稳定的非线性形式,不能直接求解出与之相对应的控制器增益和扰动观测器增益。因此定理4.2运用了费舍尔引理给出了可求解控制器增益K和扰动观测器增益L的LM。
定理4.2:对于给定的正常数b1, b2,μ, αi,i∈{1,2,3,4},如果存在正定矩阵P1gt;0," P2gt;0," Rgt;0和矩阵Q1,Q2,Q3,Q4以及M、N、Z使得如下表示的不等式(15)成立:
Λ=Λ11Λ12Λ13Λ14Λ15Λ160*Λ22Λ23Λ24Λ250Λ27**Λ33Λ34000***Λ44000****Λ5500*****Λ660******Λ77lt;0(15)
其中:
Λ11=He(P1A+b1B(I-ρ)NC)+
(α-11+α-13)ET1E1+R-He(Q1)Λ12=P1B(I-ρ)V+(MCA-b2BρNC)T-Q4Λ13=P1Ad-Q2+QT1Λ14=QT1-Q3Λ15=P1B(I-ρ)V-b1B(I-ρ)Z+μ(NC)TΛ16=P1DΛ22=He(P2W+MCB(I-ρ)V)Λ23=MCAd+QT4Λ24=QT4Λ25=b2BρZ-MCBρΛ27=MCDΛ33=(α-12+α-14)ET2E2+(τ·-1)R+QT2+Q2
Λ34=Q3+QT2Λ44=He(Q3)Λ55=-μHe(Z)Λ66=-(α1+α2)-1IΛ77=-(α3+α4)-1I
则闭环系统和扰动观测器误差都趋于渐近稳定。其中选取控制器增益K=Z-1N,扰动观测器增益L=P-12M.
证明:定理4.1可以转化为如下表达(16):
H⊥TPH⊥lt;0(16)
P=Γ0*0,H⊥=H⊥1H⊥2H⊥1=diag{I,I,I,I}H⊥2=[KC""" 0""" 0""" 0]
为了对Λ中出现的非线性部分进行解耦,于是引入了引理2,(16)可以写为如下(17):
P+He(SH)lt;0(17)
其中:
H=(KC,0,0,0,-I)S=(ST1,ST2,0,0,μZT)TS1=b1B(I-ρ)Z-P1B(I-ρ)S2=-b2BρZ+MCBρ
He(SH)=Δ11Δ1200Δ15*000Δ25**000***00****Δ55(18)
Δ11=He(b1B(I-ρ)NC-P1B(I-ρ)KC)Δ12=(-b2BρNC+MCBρ)Δ15=P1B(I-ρ)-b1B(I-ρ)Z+μ(NC)TΔ25=b2BρZ-MCBρΔ55=-μHe(Z)
可以求得P+He(SH)lt;0的矩阵表达式如下所示(19):
Θ=Θ11Θ12Θ13Θ14Θ15*Θ22Θ23Θ24Θ25**Θ33Θ340***Θ440****Θ55lt;0(19)
Θ11=He(P1A+b1B(I-ρ)NC))+
(α1+α2)P1DDTP1+(α-11+α-13)ET1E1+R-He(Q1)Θ12=P1B(I-ρ)V+(MCA-b2BρNC)T-Q4Θ13=P1Ad-Q2+QT1Θ14=QT1-Q3Θ15=P1B(I-ρ)-b1B(I-ρ)Z+μ(NC)TΘ22=He(P2W+MCB(I-ρ)V)+
(α3+α4)P2LCDDTCTLTP2Θ23=MCAd+QT4Θ33=(α-12+α-14)ET2E2+(τ·-1)R+He(Q2)Θ24=QT4Θ25=b2BρZ-MCBρΘ34=QT2+Q3Θ44=He(Q3)Θ55=-μHe(Z)
对上式(19)进行Schur展开可以得到定理4.2的不等式,证明完毕。
当ρ=0时,定理4.2可以变为一般形式,即没有考虑执行器故障。
定理4.3:对于给定的正常数b1, b2,μ, αi,i∈1,2,3,4,如果存在正定矩阵P1gt;0," P2gt;0," Rgt;0和矩阵Q1,Q2,Q3,Q4以及M,N,Z使得如下表示的不等式(20)成立:
Ω=Ω11Ω12Ω13Ω14Ω15Ω160*Ω22Ω23Ω2400Ω27**Ω33Ω34000***Ω44000****Ω5500*****Ω660******Ω77lt;0(20)
Ω11=He(P1A+b1BNC)+(α-11+α-13)ET1E1-He(Q1)Ω12=P1BV+(MCA)T-Q4Ω13=P1Ad-Q2+QT1Ω14=QT1-Q3Ω15=P1B-b1BZ+(b2NC)TΩ16=P1DΩ22=He(P2W+MCBV)Ω23=MCAd+QT4Ω24=QT4Ω27=MCDΩ33=(α-12+α-14)ET2E2+(τ·-1)R+He(Q2)Ω34=QT2+Q3Ω44=He(Q3)Ω55=He(-b2Z)Ω66=-(α1+α2)-1IΩ77=-(α3+α4)-1I
则系统趋近于渐进稳定,同时选取控制器增益K=Z-1N,扰动观测器增益L=P-12M.
5 仿真算例
为了验证所提出的扰动观测器控制方法,取如下二阶系统,根据系统的特性设计扰动观测器,估计并补偿系统中的未知扰动。需要考虑观测器的带宽,覆盖系统可能遭受的各类扰动频率。利用仿真结果评估所设计扰动观测器的性能,取:
Α=2.8-1.7-1.5-1.2
Αd=0.90.7-0.5-1
B=-62
D=1001
E1=0.02-0.01-0.010.02
E2=0.03000.03
W=00.5-0.50
V=20
C=10
选取其他参数为τ·=0.2,α1=α2=α3=α4=1,b1=10,b2=0.1,μ=1,ρ=0.8,ρ-=0。
通过求解定理4.2可以分别求出控制器增益K和扰动观测器增益L:
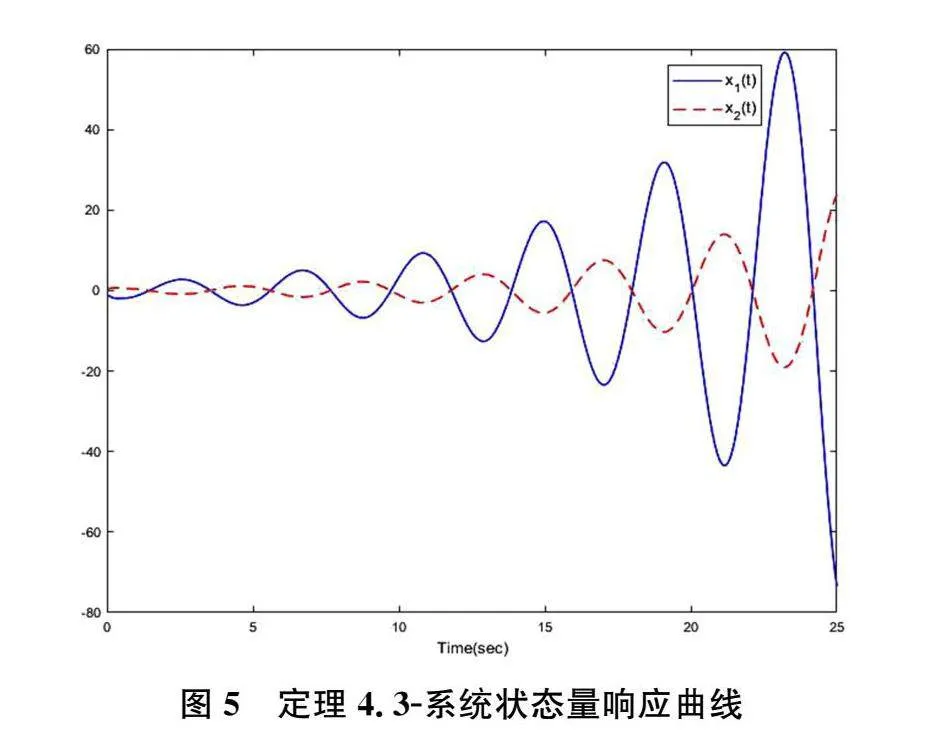
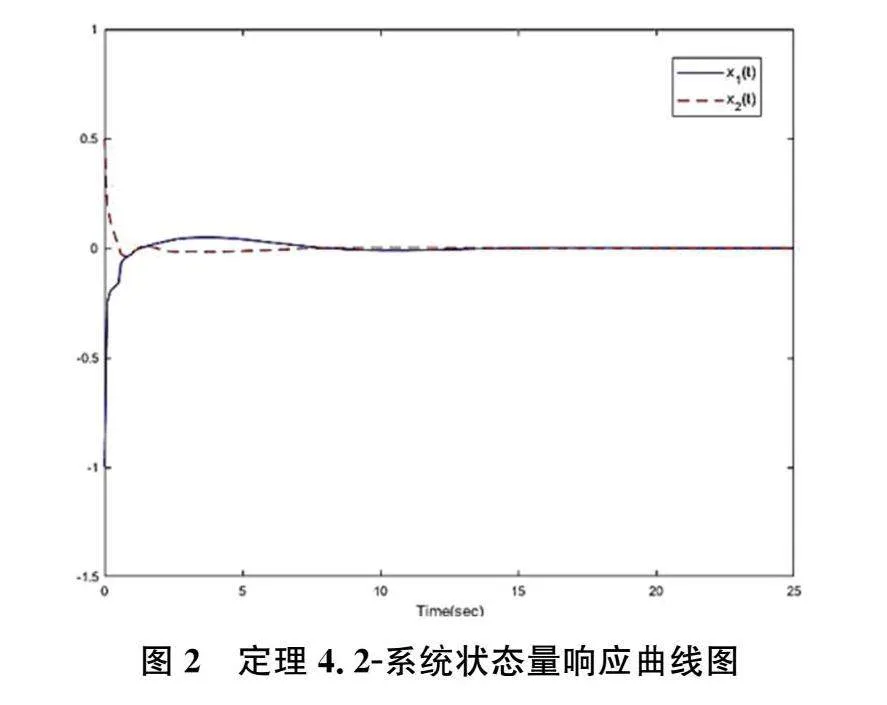
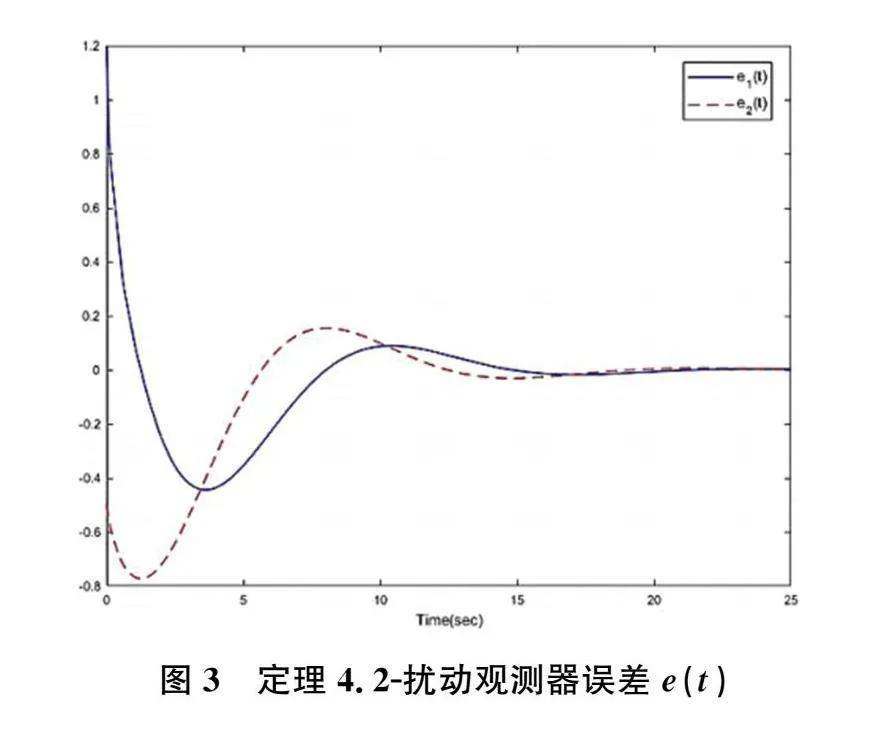
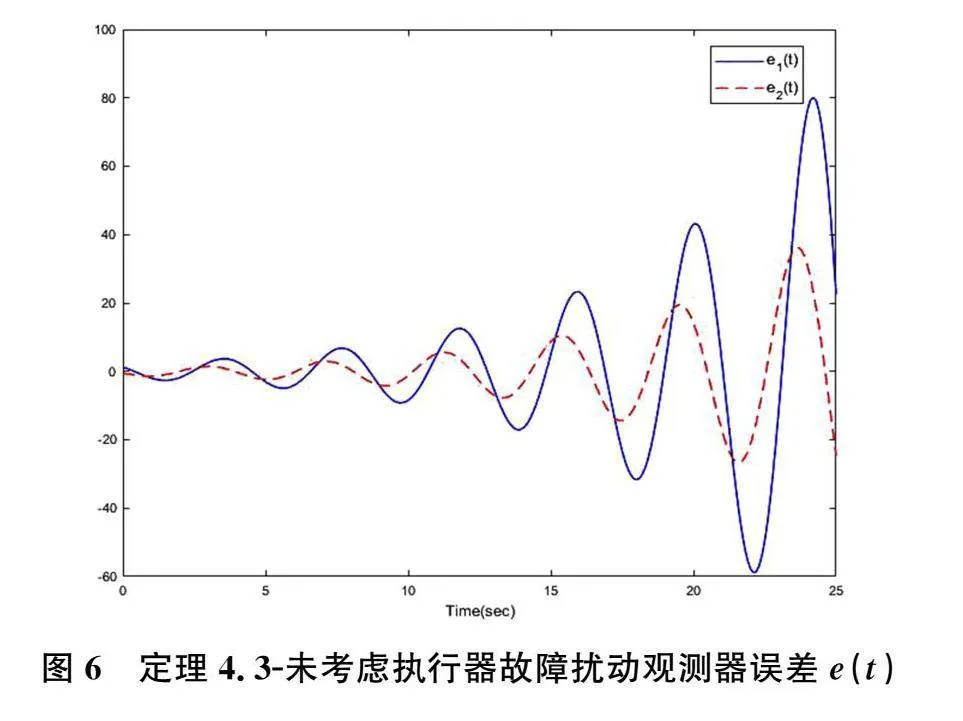
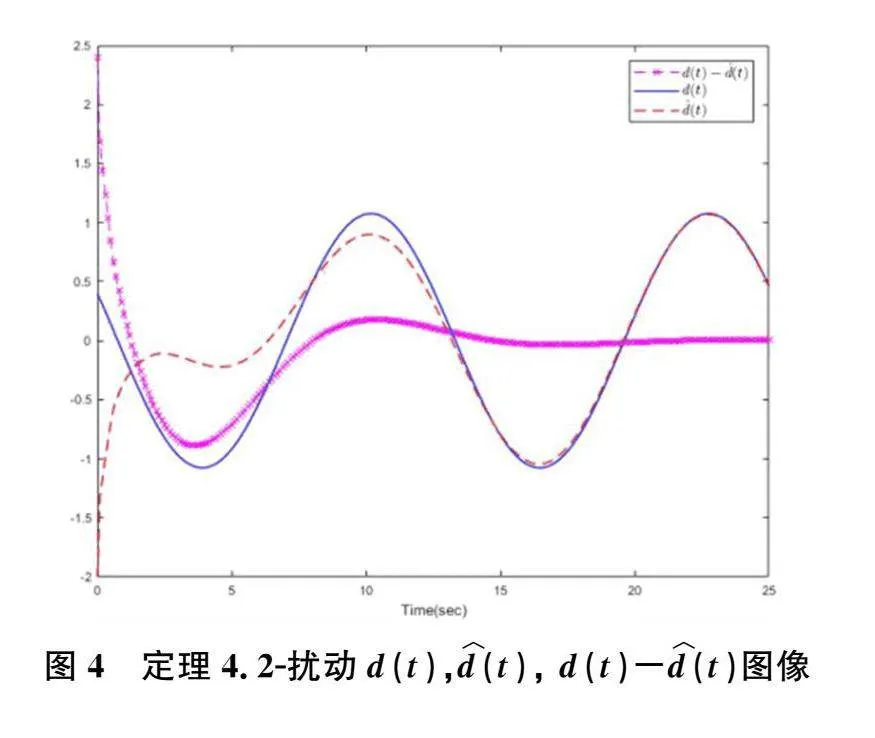
K=22.5073,""" L=0.03230.0012T,假设初始状态为x0=[-1,0.5]T,并且故障参数ρ=0.75,则系统状态响应曲线,扰动观测器估计误差e(t)及扰动估计误差d(t)-d︿(t)分别如图(3),图(4)所示,并且与没有考虑执行器故障的对应图像图(5)、图(6)、图(7)做了对比。
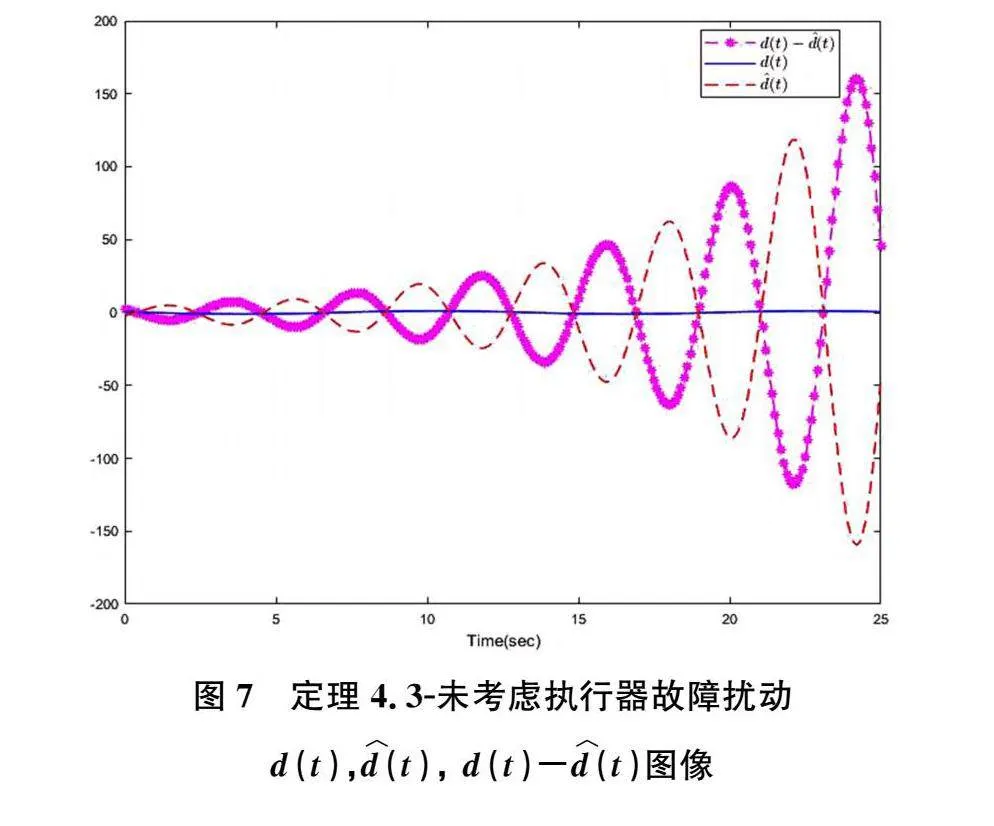
通过上述仿真图3、图4可以看出,基于输出反馈的扰动观测器的可靠控制器可以很好地追踪扰动量,其动态性能的反应速度优于系统本身的运行速度,使得扰动估计误差收敛趋近于零,同时图2中表明系统状态也趋于渐近稳定,仿真结果达到了系统设计策略的预期效果。与此同时,通过图5、图6、图7可以看出,系统状态以及扰动估计误差都没有收敛,不能够对于外部扰动进行精准地追踪。
综合上述图像可知:考虑执行器故障的系统的控制策略比没有考虑的性能更加可靠,进一步提高了容错性能。
6 小结
在基于扰动观测器的基础上,针对系统状态难获取且存在执行器故障的时滞系统,在不确定性与外界扰动下,采用输出反馈控制器解决问题。通过设计此控制器,并运用线性矩阵不等式方法求解参数耦合,为相关时滞系统的处理提供有效思路。相比H∞控制充分利用了扰动的信息,降低了系统的保守性,扰动构造能很好地对现实中真实存在的扰动进行描述。同时给出了没有考虑执行器故障下的系统镇定条件,通过仿真实验将考虑执行器故障和没有考虑执行器故障作了对比,由扰动观测器输出和系统输出反馈构成的复合控制策略可以很好地达到预期效果。
[参 考 文 献]
[1]
J H KIM.Delay and its time-derivative dependent robust stability of time-delayed linear systems with uncertainty[J].IEEE Transaction on Automatic Control,2001,46(5):789-792.
[2] M WU,Y H SHE,G P LIU.Delay-dependent criteria for robust stability of time-varying delay systems[J].Automatic,2004,40(6):1435-1439.
[3] YONG HE,M WU,J H SHE,et al.Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays[J].Systems and Control Letters,2004,51(1):57-65.
[4] Y H ROH,J H OH.Robust stabilization ofuncertain input-delay systems by sliding mode control with delay compensation[J].Automatic,1999,35(11):1861-1865.
[5] C Y KAO,A RANTZER.Stability analysis ofsystems with uncertain time-varying delays[J].Automatic,2007,43(6):959-970.
[6] Q L HAN.A new delay-dependent absolute stability criterion for a class of nonlinear neutral systems[J].Automatic,2008,44(1):272-277.
[7] 代时雨,刘淑琴.带有Markov切换的高阶扰动的Holling-Tanner模型动力学分析[J].东北师大学报(自然科学版),2023,55(3):11-17.
[8] 谢蓉,王新民,巩建英.范数有界型参数不确定性系统的概率鲁棒H∞控制方法[J].控制与决策,2014,29(7):1301-1305.
[9] 孙立明,杨博.基于扰动观测器的电力系统鲁棒滑模控制器设计[J].电力系统保护与控制,2020,48(20):124-132.
[10] LIU QUN,JIANG DAQING.Periodic Solution and Stationary Distribution of Stochastic Predator Prey Models with Higher-Order Perturbation[J].Journal of Nonlinear Science,2018,28(4):423-442.
[11] FU J,JIANG D.Qualitative analysis of astochastic ratio dependent Holling-Tanner system[J].Acta Math Sci,2018,38(2):429-440.
[12] LEE W I,LEE S Y,PARK P.A combined reciprocal convexity approach for stability analysis of static neural networks with" interval" timevarying delays[J].Neurocomputing,2016,74(9):1-23.
[13] Seuret A,Gouaisbaut F.Wirtinger basedi-ntegral inequality:Application to timedelay systems[J].Automatica,2013,49(5):2860-2866.
[14] ZHANG C K,HE Y, L. JIANG.Stability analysis of systems" with time-varying" delay viarel-axed integral inequalities[J].Systems and ControlLetters,2016,92(9):52-61.
The Actuator Failure and Feedback Control for Time-varying Delays Systems Based on a Disturbance Observer
Gao Laixin ,Li Lingchun
Abstract: For a class of time-delay systems with external disturbances and uncertainties, a disturbance observer based on output feedback and a disturbance compensation controller are constructed when the actuator failure happens and the system state are unknowable. Then, the stability of the system is judged by the Lyapunov second method. The sufficient conditions for the asymptotic stability of the system are given in the form of linear matrix inequalities. At the same time, the Finsler lemma is used to deal with the coupling problem of the controller synthesize. Finally, through the numerical simulation experiments, the effectiveness of the disturbance rejection control method based on disturbance observer is verified. Further, the fault tolerant control is more reliable than the control algorithm which does not consider the actuator failure to maintain the system and improve the performance of the system.
Key words:disturbance observer;time delay system; Markov system;linear matrix inequalit
责任编辑:陈星宇
